数据结构c版(3)——排序算法
本章我们来学习一下数据结构的排序算法!
目录
1.排序的概念及其运用
1.1排序的概念
1.2 常见的排序算法
2.常见排序算法的实现
2.1 插入排序
2.1.1基本思想:
2.1.2直接插入排序:
2.1.3 希尔排序( 缩小增量排序 )
2.2 选择排序
2.2.1基本思想:
2.2.2 直接选择排序:
2.2.3 堆排序
2.3 交换排序
2.3.1冒泡排序
2.3.2 快速排序
1. hoare版本
2. 挖坑法
3. 前后指针版本 编辑
2.3.2 快速排序优化
2.3.3 快速排序非递归
2.4 归并排序
2.5 非比较排序
3.排序算法复杂度及稳定性分析
1.排序的概念及其运用
1.1排序的概念
(1)排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
(2)稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次 序保持不变,即在原序列中, r [ i ] = r [ j ],且 r [ i ] 在 r [ j ] 之前,而在排序后的序列中, r [ i ] 仍在 r [ j ]之前,则称这种排序算法是稳定的;否则称为不稳定的。
(3)内部排序:数据元素全部放在内存中的排序。
(4)外部排序:数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序。
1.2 常见的排序算法
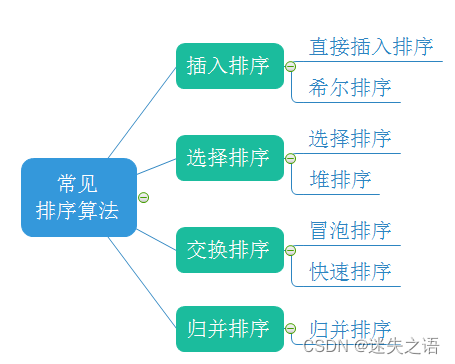
2.常见排序算法的实现
2.1 插入排序
2.1.1基本思想:
直接插入排序是一种简单的插入排序法,其基本思想是:
把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列 。
2.1.2直接插入排序:
// 时间复杂度:O(N^2) 逆序
// 最好的情况:O(N) 顺序有序
void InsertSort(int* a, int n)
{// [0, end] end+1for (int i = 0; i < n-1; ++i){int end = i;int tmp = a[end + 1];while (end >= 0){if (tmp > a[end]){a[end + 1] = a[end];--end;}else{break;}}a[end + 1] = tmp;}
}直接插入排序的特性总结:1. 元素集合越接近有序,直接插入排序算法的时间效率越高。2. 时间复杂度: O(N^2)3. 空间复杂度: O(1) ,它是一种稳定的排序算法。4. 稳定性:稳定
2.1.3 希尔排序( 缩小增量排序 )

代码案例:
// 平均O(N^1.3)
void ShellSort(int* a, int n)
{int gap = n;// gap > 1时是预排序,目的让他接近有序// gap == 1是直接插入排序,目的是让他有序while (gap > 1){//gap = gap / 2;gap = gap / 3 + 1;for (int i = 0; i < n - gap; ++i){int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}希尔排序的特性总结:1. 希尔排序是对直接插入排序的优化。2. 当 gap > 1 时都是预排序,目的是让数组更接近于有序。当 gap == 1 时,数组已经接近有序的了,这样就会很快。这样整体而言,可以达到优化的效果。我们实现后可以进行性能测试的对比。3. 希尔排序的时间复杂度不好计算,因为 gap 的取值方法很多,导致很难去计算,因此在好些书中给出的希尔排序的时间复杂度都不固定:《数据结构 (C 语言版 ) 》 --- 严蔚敏
《数据结构-用面相对象方法与C++描述》--- 殷人昆
因为gap是按照Knuth提出的方式取值的,而且Knuth进行了大量的试验统计,我们暂时就按照:
到
来算。
4. 稳定性:不稳定
2.2 选择排序
2.2.1基本思想:
2.2.2 直接选择排序:

代码案例:
// 时间复杂度:O(N^2)
// 最好的情况下:O(N^2)
void SelectSort(int* a, int n)
{int begin = 0, end = n - 1;while (begin < end){int mini = begin, maxi = begin;for (int i = begin + 1; i <= end; ++i){if (a[i] < a[mini]){mini = i;}if (a[i] > a[maxi]){maxi = i;}}Swap(&a[begin], &a[mini]);if (maxi == begin){maxi = mini;}Swap(&a[end], &a[maxi]);++begin;--end;}
}
直接选择排序的特性总结:1. 直接选择排序思考非常好理解,但是效率不是很好。实际中很少使用。2. 时间复杂度: O(N^2)3. 空间复杂度: O(1)4. 稳定性:不稳定
2.2.3 堆排序
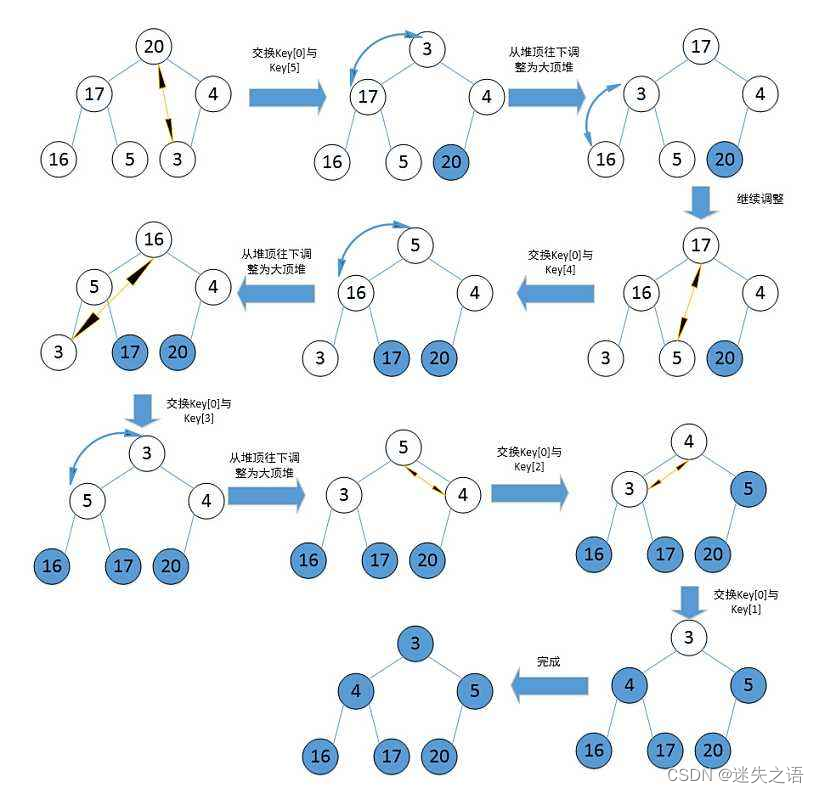
代码案例:
void AdjustDown(int* a, int size, int parent)
{int child = parent * 2 + 1;while (child < size){// 假设左孩子小,如果解设错了,更新一下if (child + 1 < size && a[child + 1] > a[child]){++child;}if (a[child] > a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}// 升序
void HeapSort(int* a, int n)
{// O(N)// 建大堆for (int i = (n - 1 - 1) / 2; i >= 0; --i){AdjustDown(a, n, i);}// O(N*logN)int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);--end;}
}堆排序的特性总结:1. 堆排序使用堆来选数,效率就高了很多。2. 时间复杂度: O(N*logN)3. 空间复杂度: O(1)4. 稳定性:不稳定
2.3 交换排序
2.3.1冒泡排序
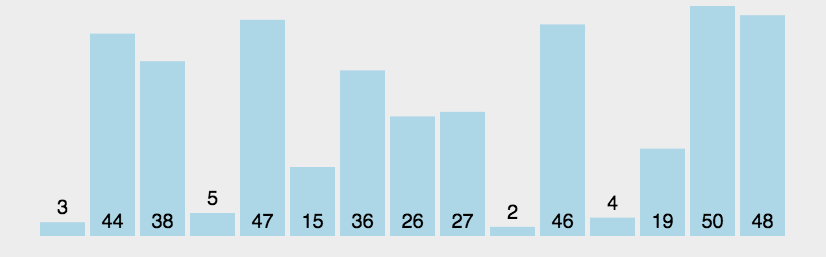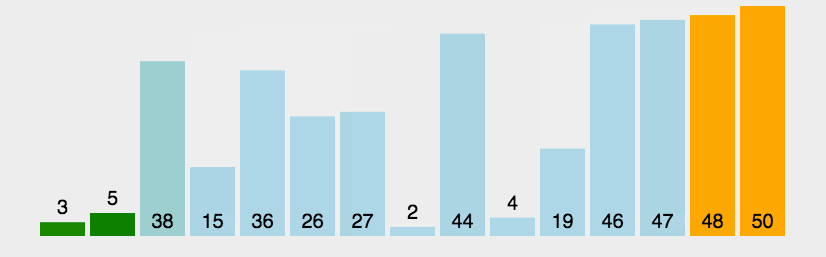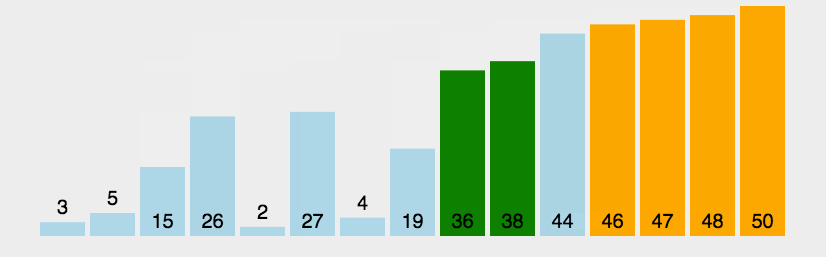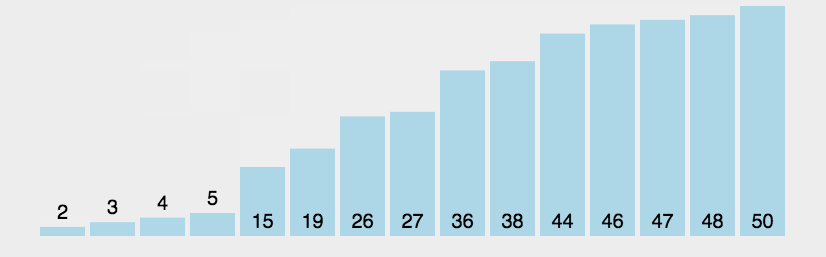
代码案例:
void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}// 时间复杂度:O(N^2)
// 最好情况是多少:O(N)
void BubbleSort(int* a, int n)
{for (int j = 0; j < n; j++){bool exchange = false;for (int i = 1; i < n-j; i++){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);exchange = true;}}if (exchange == false)break;}冒泡排序的特性总结:1. 冒泡排序是一种非常容易理解的排序2. 时间复杂度: O(N^2)3. 空间复杂度: O(1)4. 稳定性:稳定
2.3.2 快速排序
代码案例:
// 假设按照升序对array数组中[left, right)区间中的元素进行排序
void QuickSort(int array[], int left, int right)
{if(right - left <= 1)return;// 按照基准值对array数组的 [left, right)区间中的元素进行划分int div = partion(array, left, right);// 划分成功后以div为边界形成了左右两部分 [left, div) 和 [div+1, right)// 递归排[left, div)QuickSort(array, left, div);// 递归排[div+1, right)QuickSort(array, div+1, right);
}int GetMidi(int* a, int begin, int end)
{int midi = (begin + end) / 2;// begin end midi三个数选中位数if (a[begin] < a[midi]){if (a[midi] < a[end])return midi;else if (a[begin] > a[end])return begin;elsereturn end;}else{//...}
}void QuickSort(int* a, int begin, int end)
{if (begin >= end)return;int midi = GetMidi(a, begin, end);Swap(&a[midi], &a[begin]);int left = begin, right = end;int keyi = begin;while (left < right){// 右边找小while (left < right && a[right] >= a[keyi]){--right;}// 左边找大while (left < right && a[left] <= a[keyi]){++left;}Swap(&a[left], &a[right]);}Swap(&a[left], &a[keyi]);keyi = left;// [begin, keyi-1] keyi [keyi+1, end]QuickSort(a, begin, keyi - 1);QuickSort(a, keyi+1, end);
}1. hoare版本

代码案例:
int PartSort1(int* a, int begin, int end)
{int midi = GetMidi(a, begin, end);Swap(&a[midi], &a[begin]);int left = begin, right = end;int keyi = begin;while (left < right){// 右边找小while (left < right && a[right] >= a[keyi]){--right;}// 左边找大while (left < right && a[left] <= a[keyi]){++left;}Swap(&a[left], &a[right]);}Swap(&a[left], &a[keyi]);return left;
}void QuickSort(int* a, int begin, int end)
{if (begin >= end)return;int keyi = PartSort1(a, begin, end);QuickSort(a, begin, keyi - 1);QuickSort(a, keyi+1, end);
}2. 挖坑法
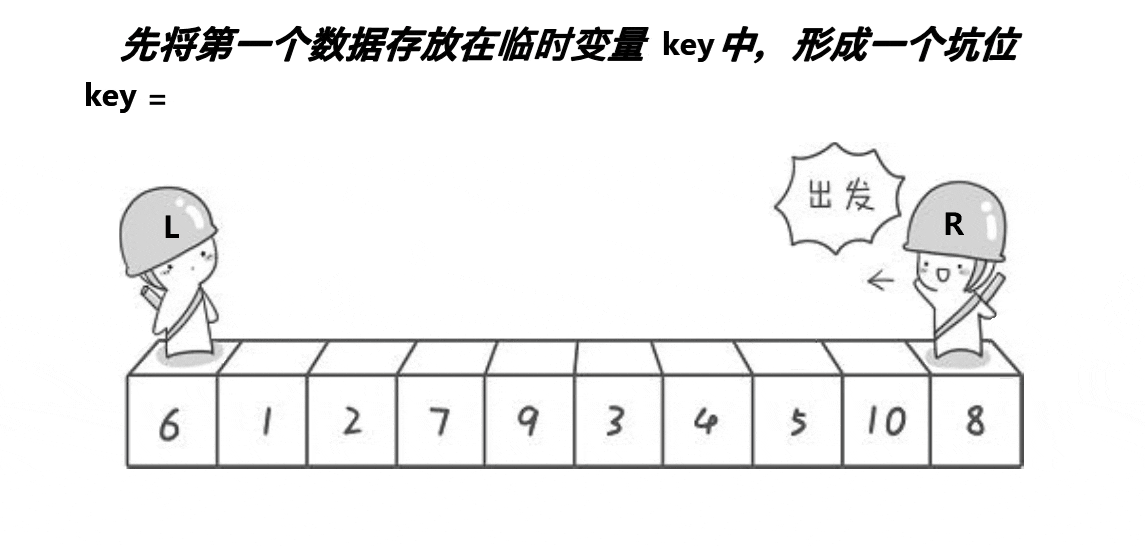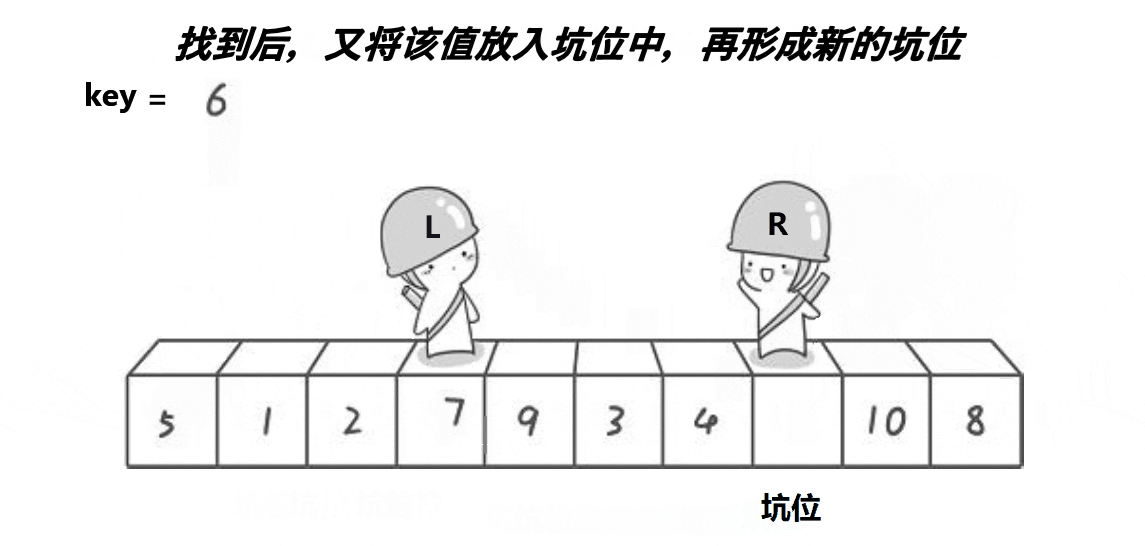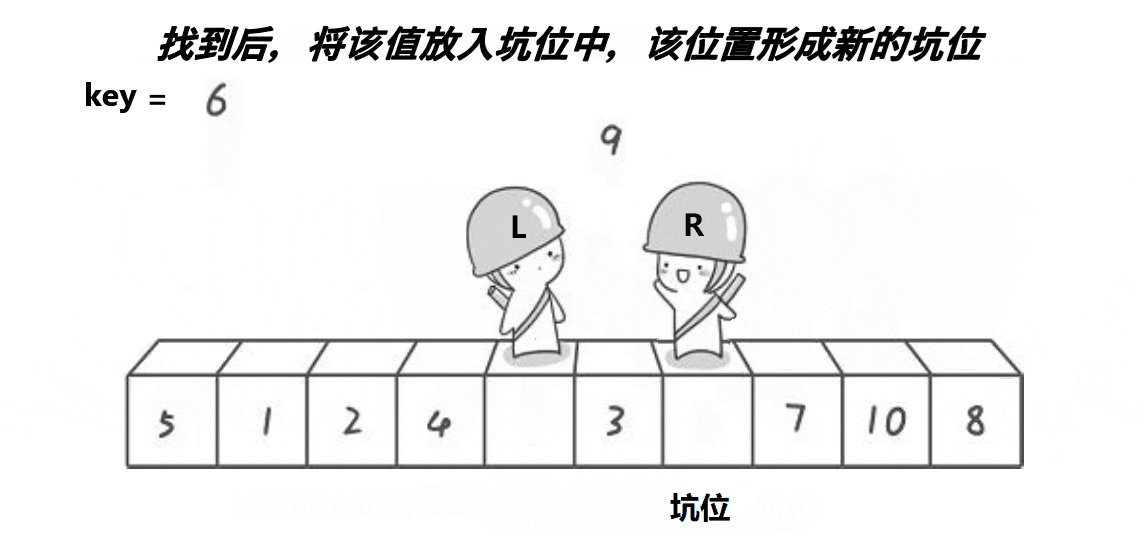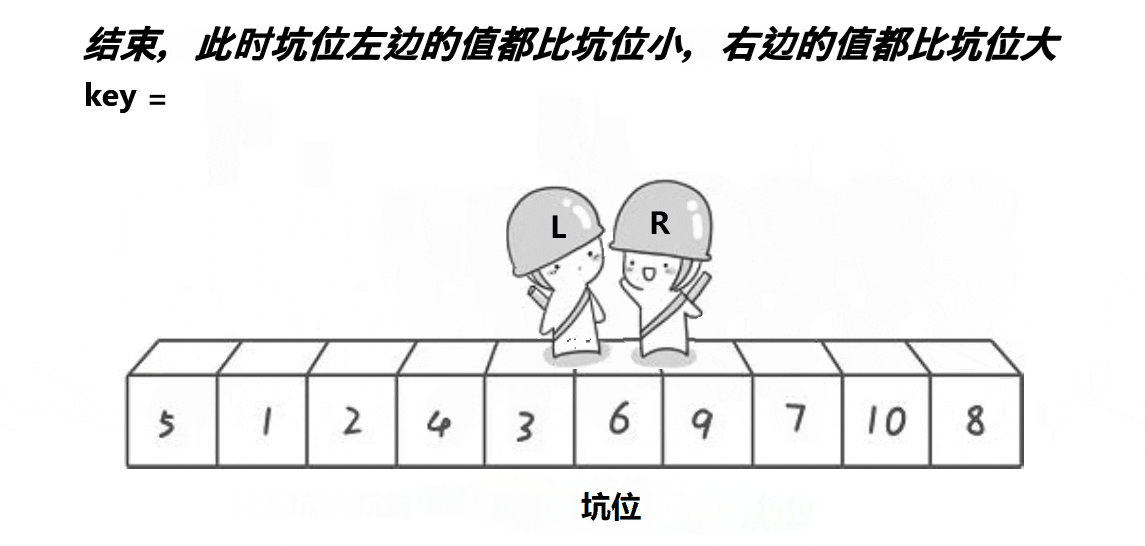
代码案例:
// 挖坑法
int PartSort2(int* a, int begin, int end)
{int midi = GetMidi(a, begin, end);Swap(&a[midi], &a[begin]);int key = a[begin];int hole = begin;while (begin < end){// 右边找小,填到左边的坑while (begin < end && a[end] >= key){--end;}a[hole] = a[end];hole = end;// 左边找大,填到右边的坑while (begin < end && a[begin] <= key){++begin;}a[hole] = a[begin];hole = begin;}a[hole] = key;return hole;
}void QuickSort(int* a, int begin, int end)
{if (begin >= end)return;int keyi = PartSort2(a, begin, end);QuickSort(a, begin, keyi - 1);QuickSort(a, keyi+1, end);
}
3. 前后指针版本 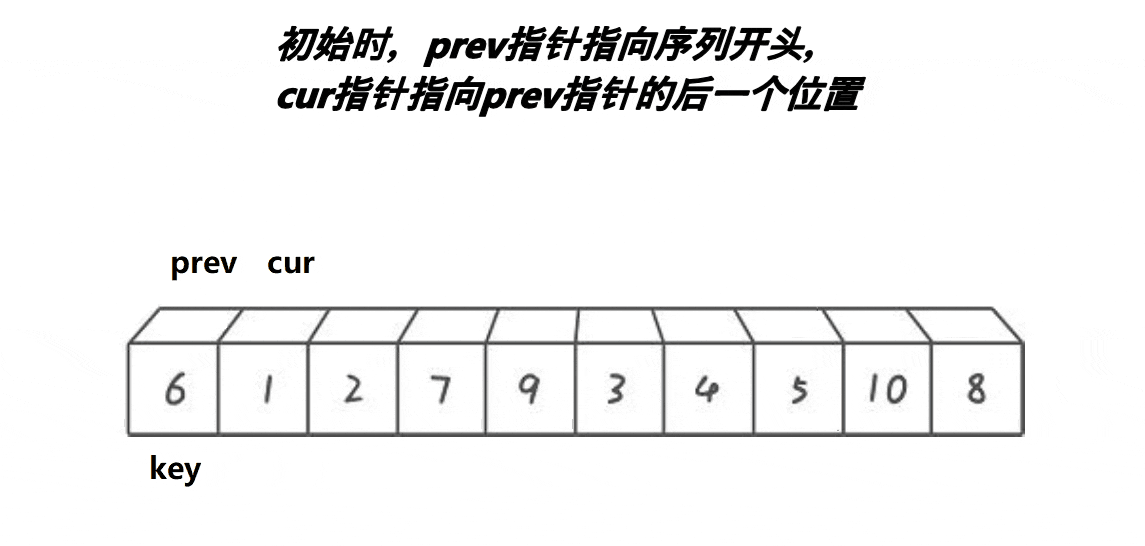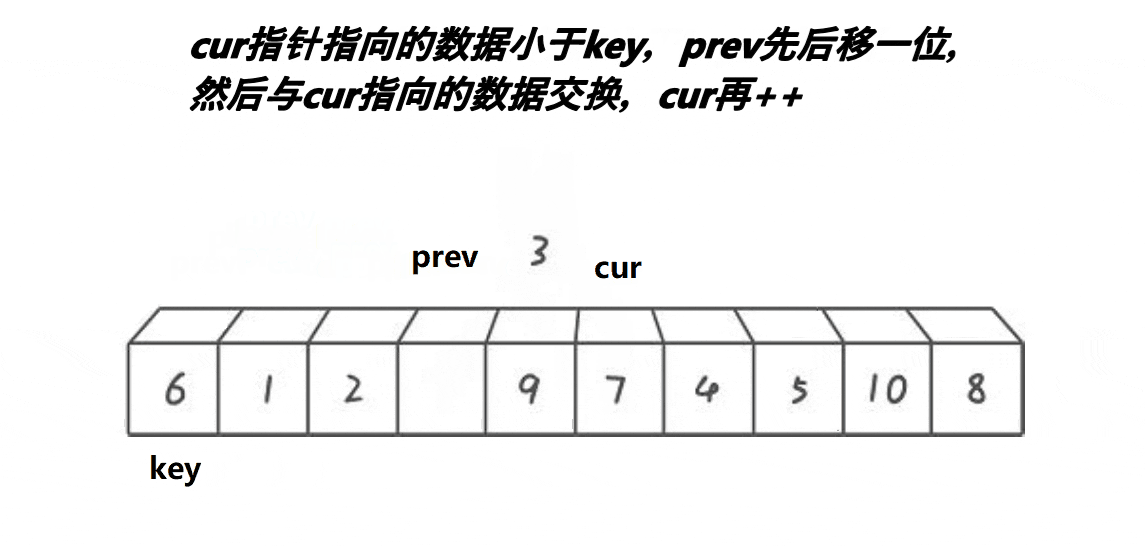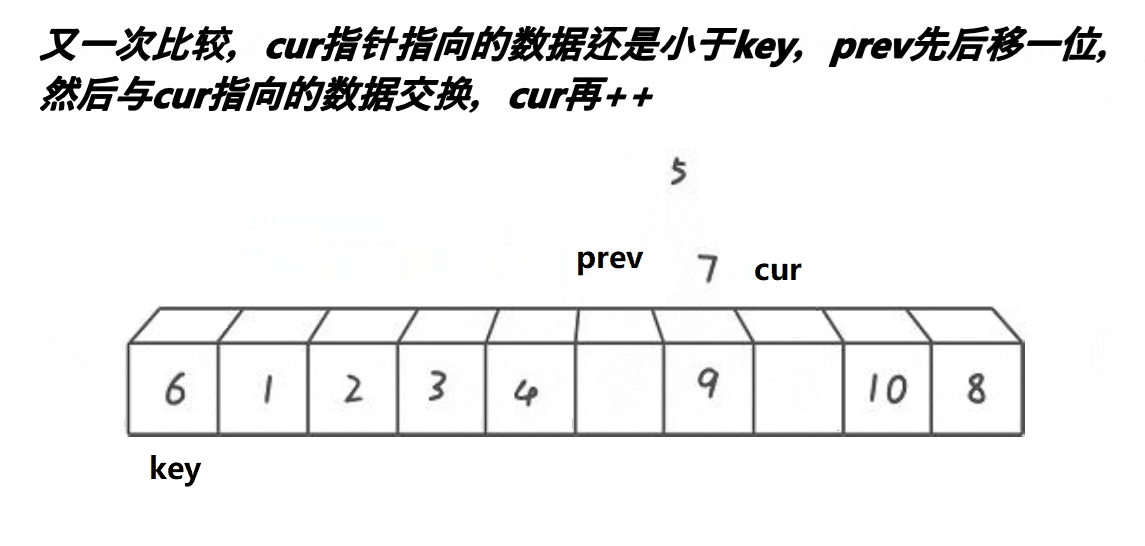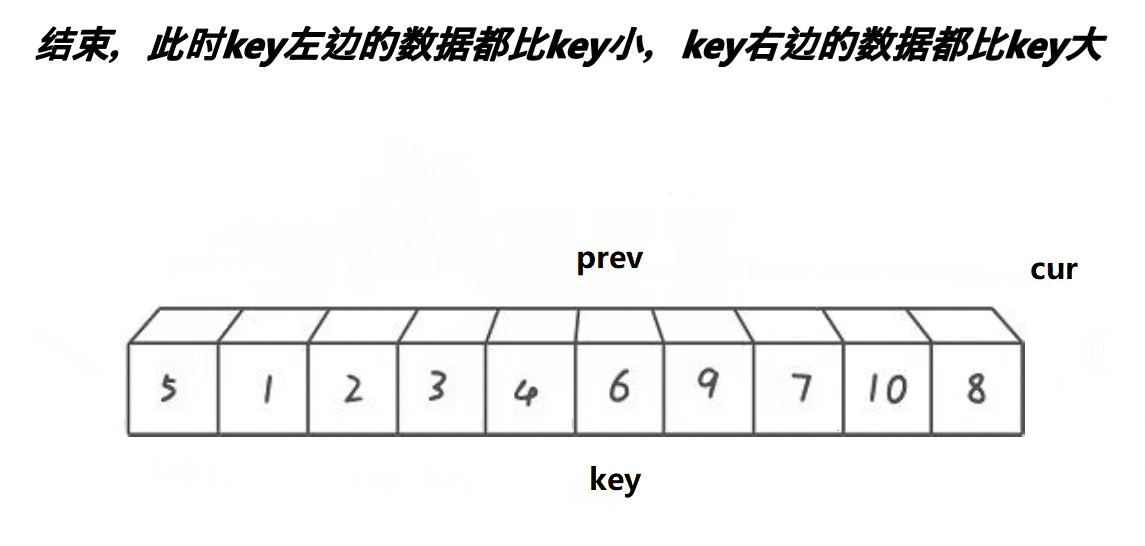
代码案例:
int PartSort3(int* a, int begin, int end)
{int midi = GetMidi(a, begin, end);Swap(&a[midi], &a[begin]);int keyi = begin;int prev = begin;int cur = prev + 1;while (cur <= end){if (a[cur] < a[keyi] && ++prev != cur)Swap(&a[prev], &a[cur]);++cur;}Swap(&a[prev], &a[keyi]);keyi = prev;return keyi;
}void QuickSort(int* a, int begin, int end)
{if (begin >= end)return;int keyi = PartSort3(a, begin, end);QuickSort(a, begin, keyi - 1);QuickSort(a, keyi+1, end);
}
2.3.2 快速排序优化
1. 三数取中法选 key2. 递归到小的子区间时,可以考虑使用插入排序

2.3.3 快速排序非递归
代码案例:
void QuickSortNonR(int* a, int left, int right)
{Stack st;StackInit(&st);StackPush(&st, left);StackPush(&st, right);while (StackEmpty(&st) != 0){right = StackTop(&st);StackPop(&st);left = StackTop(&st);StackPop(&st);if(right - left <= 1)continue;int div = PartSort1(a, left, right);// 以基准值为分割点,形成左右两部分:[left, div) 和 [div+1, right)StackPush(&st, div+1);StackPush(&st, right);StackPush(&st, left);StackPush(&st, div);}StackDestroy(&s);
}快速排序的特性总结:1. 快速排序整体的综合性能和使用场景都是比较好的,所以才敢叫 快速 排序2. 时间复杂度: O(N*logN)
3. 空间复杂度: O(logN)4. 稳定性:不稳定
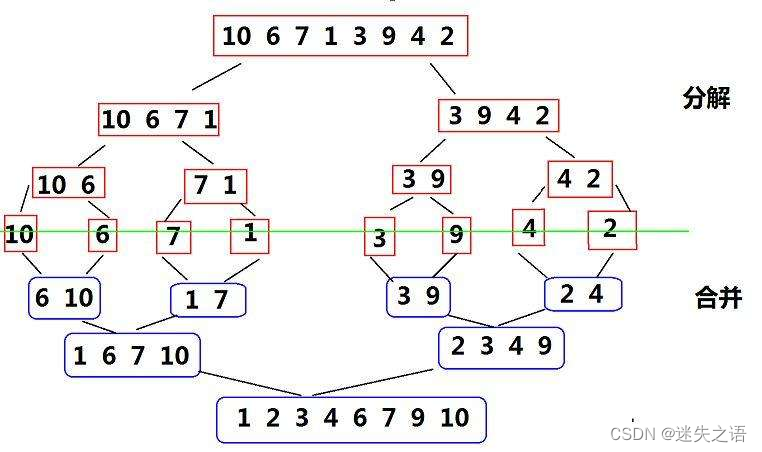
2.4 归并排序
基本思想:归并排序(MERGE-SORT )是建立在归并操作上的一种有效的排序算法 , 该算法是采用分治法( Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。 归并排序核心步骤:

代码案例:
void _MergeSort(int* a, int begin, int end, int* tmp)
{if (begin >= end)return;int mid = (begin + end) / 2;// [begin, mid][mid+1, end]_MergeSort(a, begin, mid, tmp);_MergeSort(a, mid+1, end, tmp);// [begin, mid][mid+1, end]归并int begin1 = begin, end1 = mid;int begin2 = mid + 1, end2 = end;int i = begin;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[i++] = a[begin1++];}else{tmp[i++] = a[begin2++];}}while(begin1 <= end1){tmp[i++] = a[begin1++];}while (begin2 <= end2){tmp[i++] = a[begin2++];}memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));
}void MergeSort(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail");return;}_MergeSort(a, 0, n - 1, tmp);free(tmp);
}//非递归法
void MergeSortNonR(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail");return;}int gap = 1;while (gap < n){printf("gap:%2d->", gap);for (size_t i = 0; i < n; i += 2 * gap){int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;// [begin1, end1][begin2, end2] 归并//printf("[%2d,%2d][%2d, %2d] ", begin1, end1, begin2, end2);// 边界的处理if (end1 >= n || begin2 >= n){break;}if (end2 >= n){end2 = n - 1;}//printf("[%2d,%2d][%2d, %2d] ", begin1, end1, begin2, end2);int j = begin1;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[j++] = a[begin1++];}else{tmp[j++] = a[begin2++];}}while (begin1 <= end1){tmp[j++] = a[begin1++];}while (begin2 <= end2){tmp[j++] = a[begin2++];}memcpy(a + i, tmp + i, sizeof(int) * (end2-i+1));}printf("\n");gap *= 2;}free(tmp);
}归并排序的特性总结:1. 归并的缺点在于需要 O(N) 的空间复杂度,归并排序的思考更多的是解决在磁盘中的外排序问题。2. 时间复杂度: O(N*logN)3. 空间复杂度: O(N)4. 稳定性:稳定
2.5 非比较排序
思想:计数排序又称为鸽巢原理,是对哈希直接定址法的变形应用。 操作步骤:1. 统计相同元素出现次数2. 根据统计的结果将序列回收到原来的序列中
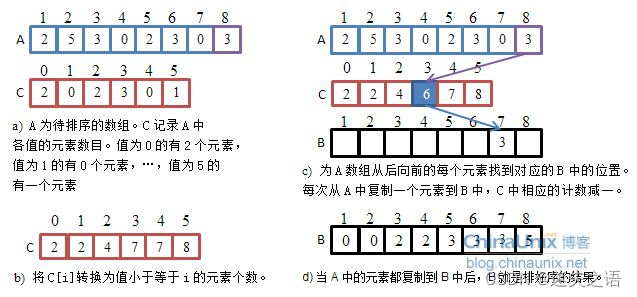
代码案例:
// 基数排序/桶排序// 计数排序
// 时间:O(N+range)
// 空间:O(range)
void CountSort(int* a, int n)
{int min = a[0], max = a[0];for (int i = 1; i < n; i++){if (a[i] < min)min = a[i];if (a[i] > max)max = a[i];}int range = max - min + 1;int* count = (int*)calloc(range, sizeof(int));if (count == NULL){printf("calloc fail\n");return;}// 统计次数for (int i = 0; i < n; i++){count[a[i] - min]++;}// 排序int i = 0;for (int j = 0; j < range; j++){while (count[j]--){a[i++] = j + min;}}
}计数排序的特性总结:1. 计数排序在数据范围集中时,效率很高,但是适用范围及场景有限。2. 时间复杂度: O(MAX(N, 范围 ))3. 空间复杂度: O( 范围 )4. 稳定性:稳定
3.排序算法复杂度及稳定性分析
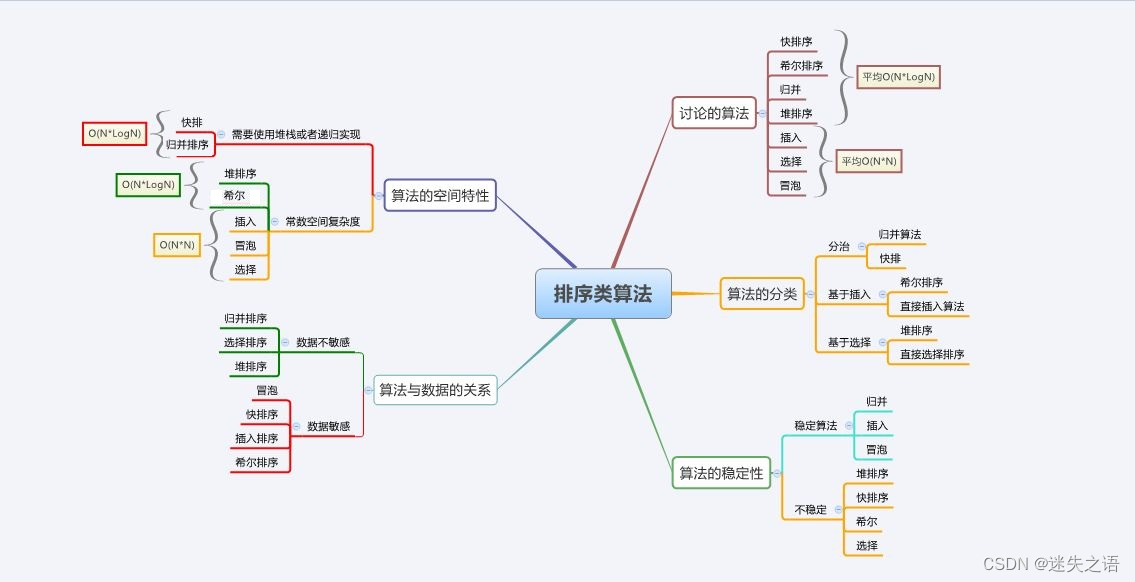
注:
(1)算法稳定性是指,待排序列中相同的值在排序后相对顺序不变,这就是算法稳定。
(2)辅助空间是指在排序的过程中开辟了新的空间。
本篇完!
相关文章:

数据结构c版(3)——排序算法
本章我们来学习一下数据结构的排序算法! 目录 1.排序的概念及其运用 1.1排序的概念 1.2 常见的排序算法 2.常见排序算法的实现 2.1 插入排序 2.1.1基本思想: 2.1.2直接插入排序: 2.1.3 希尔排序( 缩小增量排序 ) 2.2 选择排序 2.2…...

《Spring Security 简易速速上手小册》第5章 高级认证技术(2024 最新版)
文章目录 5.1 OAuth2 和 OpenID Connect5.1.1 基础知识详解OAuth2OpenID Connect结合 OAuth2 和 OIDC 5.1.2 重点案例:使用 OAuth2 和 OpenID Connect 实现社交登录案例 Demo 5.1.3 拓展案例 1:访问受保护资源案例 Demo测试访问受保护资源 5.1.4 拓展案例…...

【七】【SQL】自连接
自连接初见 数据库中的自连接是一种特殊类型的SQL查询,它允许表与自身进行连接,以便查询表中与其他行相关联的行。自连接通常用于处理那些存储在同一个表中的但彼此之间具有层级或关系的数据。为了实现自连接,通常需要给表使用别名ÿ…...

C语言while 与 do...while 的区别?
一、问题 while 语句和 do...while 语句类似,都是要判断循环条件是否为真。如果为真,则执⾏循环体,否则退出循环。它们之间有什么区别呢? 二、解答 while 语句和 do..while 语句的区别在于:do..while 语句是先执⾏⼀次…...

RK3568平台开发系列讲解(基础篇)内核错误码
🚀返回专栏总目录 文章目录 一、指针的分类二、错误码三、错误码使用案例沉淀、分享、成长,让自己和他人都能有所收获!😄 一、指针的分类 二、错误码 在 Linux 内核中,所谓的错误指针已经指向了内核空间的最后一页,例如,对于一个 64 位系统来说,内核空间最后地址为 0…...
)
点云从入门到精通技术详解100篇-基于点云网络和 PSO 优化算法的手势估计(续)
目录 3 深度图像处理及转化 3.1 双目深度摄像原理及深度图的获取 3.1.1 理想化双目深度相机成像...
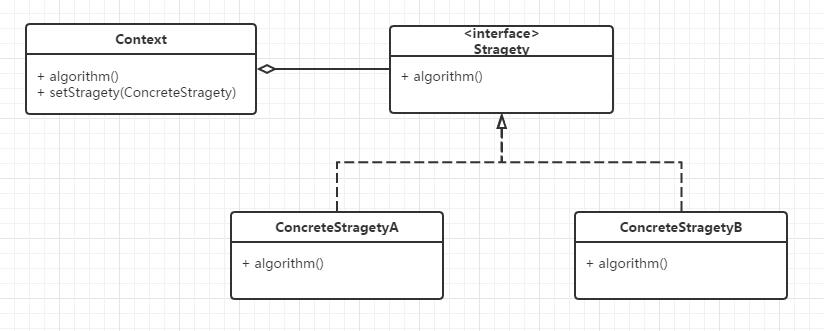
设计模式(十一)策略模式
请直接看原文:设计模式(十一)策略模式_某移动支付系统在实现账户资金转入和转出时需要进行身份验证,该系统为用户提供了-CSDN博客 ----------------------------------------------------------------------------------------------------------------…...

Java 计算某年份二月的天数
一、实验任务 要求编写一个程序,从键盘输入年份,根据输入的年份计算这一年的2月有多少天。 二、实验内容 三、实验结果 四、实现逻辑和步骤 (1)使用scanner类实现程序使用键盘录入一个年份。 (2)使用if语…...
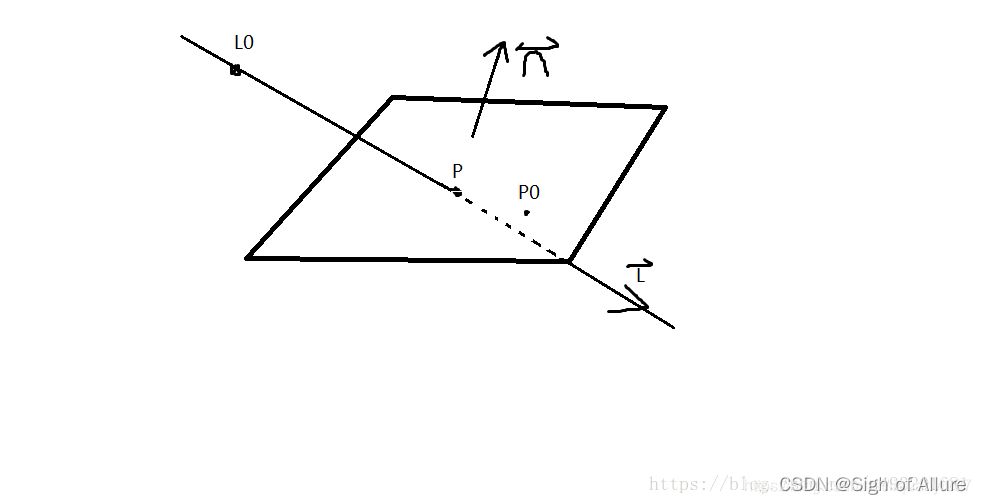
unity 数学 如何计算线和平面的交点
已知一个平面上的一点P0和法向量n,一条直线上的点L0和方向L,求该直线与该平面的交点P 如下图 首先我们要知道向量归一化点乘之后得到就是两个向量的夹角的余弦值,如果两个向量相互垂直则值是0,小于0则两个向量的夹角大于90度,大于…...

Mysql DATETIME与TIMESTAMP的区别
TIMESTAMP的取值范围小,并且TIMESTAMP类型的日期时间在存储时会将当前时区的日期时间值转换为时间标准时间值,检索时再转换回当前时区的日期时间值。 而DATETIME则只能反映出插入时当地的时区,其他时区的人查看数据必然会有误差的。 DATETI…...

hadoop基础
启动Hadoop cd /usr/local/hadoop ./sbin/start-dfs.sh #启动hadoop打开 ./bin/hdfs dfs ./bin/hdfs dfs -ls 针对 DataNode 没法启动的解决方法 cd /usr/local/hadoop ./sbin/stop-dfs.sh # 关闭 rm -r ./tmp # 删除 tmp 文件,注意这会删除 HDFS 中原有的…...

2024目前三种有效加速国内Github
大家好我是咕噜美乐蒂,很高兴又和大家见面了!截至2024年,国内访问 GitHub 的速度受到多种因素的影响,包括网络封锁、地理距离、网络带宽等。为了提高国内用户访问 GitHub 的速度,以下是目前较为有效的三种加速方式&…...
2024高频前端面试题 HTML 和 CSS 篇
JS和ES6 篇: 2024高频前端面试题 JavaScript 和 ES6 篇-CSDN博客 一 . HTML 篇 1. H5有什么新特性 1) 语义化标签 用正确的标签做正确的事情。 html 语义化让页面的内容结构化,结构更清晰,便于对浏览器、搜索引擎解析&…...

LeetCode 100231.超过阈值的最少操作数 I
给你一个下标从 0 开始的整数数组 nums 和一个整数 k 。 一次操作中,你可以删除 nums 中的最小元素。 你需要使数组中的所有元素都大于或等于 k ,请你返回需要的 最少 操作次数。 示例 1: 输入:nums [2,11,10,1,3], k 10 输…...
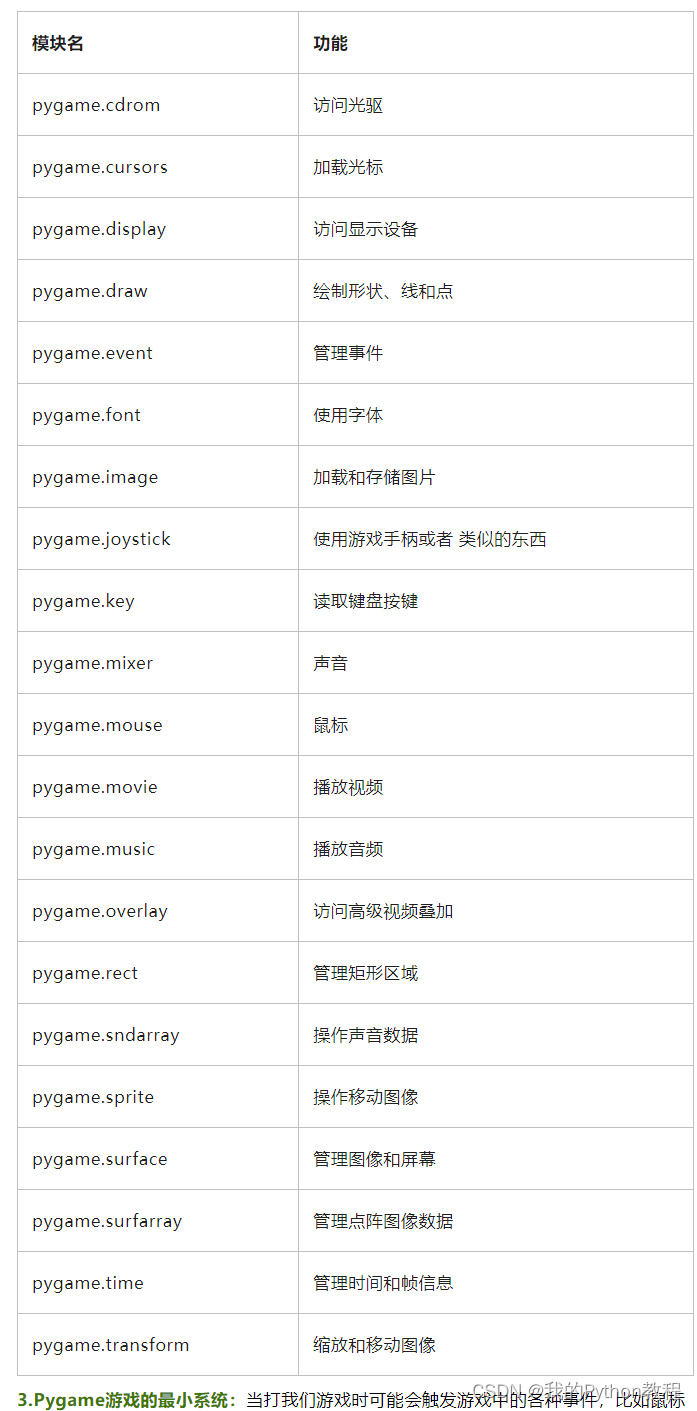
Pygame教程01:初识pygame游戏模块
Pygame是一个用于创建基本的2D游戏和图形应用程序。它提供了一套丰富的工具,让开发者能够轻松地创建游戏和其他图形应用程序。Pygame 支持许多功能,包括图像和声音处理、事件处理、碰撞检测、字体渲染等。 Pygame 是在 SDL(Simple DirectMed…...

HTML和CSS (前端共三篇)【详解】
目录 一、前端开发介绍 二、HTML入门 三、HTML基础标签 四、CSS样式修饰 五、HTML表格标签 六、HTML表单标签 一、前端开发介绍 web应用有BS和CS架构两种,其中我们主要涉及的是BS架构。而BS架构里,B(Browser浏览器)是客户端的…...
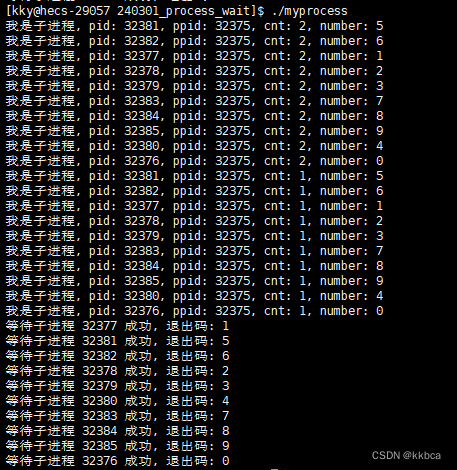
Linux——进程控制(二)进程等待
目录 前言 一、进程等待 二、如何进行进程等待 1.wait 2.waitpid 2.1第二个参数 2.2第三个参数 3. 等待多个进程 三、为什么不用全局变量获取子进程的退出信息 前言 前面我们花了大量的时间去学习进程的退出,退出并不难,但更深入的学习能为本…...

多线程导入excel
设置线程池参数,创建线程池 corePoolSize要保留在池中的线程数,即使它们是空闲的,除非{code - allowCoreThreadTimeOut}被设置maximumPoolSize允许在池中的最大线程数keepAliveTime当线程数大于核心时,这是多余的空闲线程将在终止…...
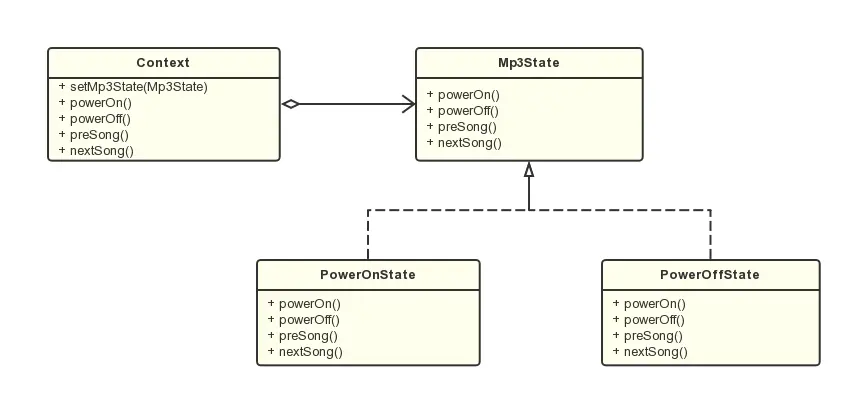
设计模式(十五)状态模式
请直接看原文:设计模式系列 ------------------------------------------------------------------------------------------------------------------------------- 前言 建议在阅读本文前先阅读设计模式(十一)策略模式这篇文章,虽说状态…...
Java基于SpringBoot的在线文档管理系统的设计与实现论文
摘 要 随着科学技术的飞速发展,社会的方方面面、各行各业都在努力与现代的先进技术接轨,通过科技手段来提高自身的优势,在线文档管理当然也不能排除在外。在线文档管理系统是以实际运用为开发背景,运用软件工程原理和开发方法&am…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...


