每日一题——LeetCode1572.矩阵对角线元素的和

方法一 遍历矩阵
如果矩阵中某个位置(x,y)处于对角线上,那么这个位置必定满足:
x=y 或 x+y = len-1 (len为矩阵长度)
var diagonalSum = function(mat) {let len = mat.length;let sum = 0;for (let i = 0; i < len; i++) {for (let j = 0; j < len; j++) {if (i == j || i + j == len - 1) {sum += mat[i][j];}}}return sum;
};消耗时间和内存情况:

方法二 枚举对角线元素:
逐行遍历,记当前行号为i,每一行的对角线元素为(i,i)和(i,len-i-1)
如果len为奇数则对角线交点会被计算两次,需要减掉一次
用len&1,如果len为奇数结果为1,len为偶数结果为0
var diagonalSum = function(mat) {let len = mat.length, mid = Math.floor(len / 2);let sum = 0;for (let i = 0; i < len; ++i) {sum += mat[i][i] + mat[i][len - 1 - i];}return sum - mat[mid][mid] * (len & 1);
};消耗时间和内存情况:

相关文章:

每日一题——LeetCode1572.矩阵对角线元素的和
方法一 遍历矩阵 如果矩阵中某个位置(x,y)处于对角线上,那么这个位置必定满足: xy 或 xy len-1 (len为矩阵长度) var diagonalSum function(mat) {let len mat.length;let sum 0;for (let i 0; i …...
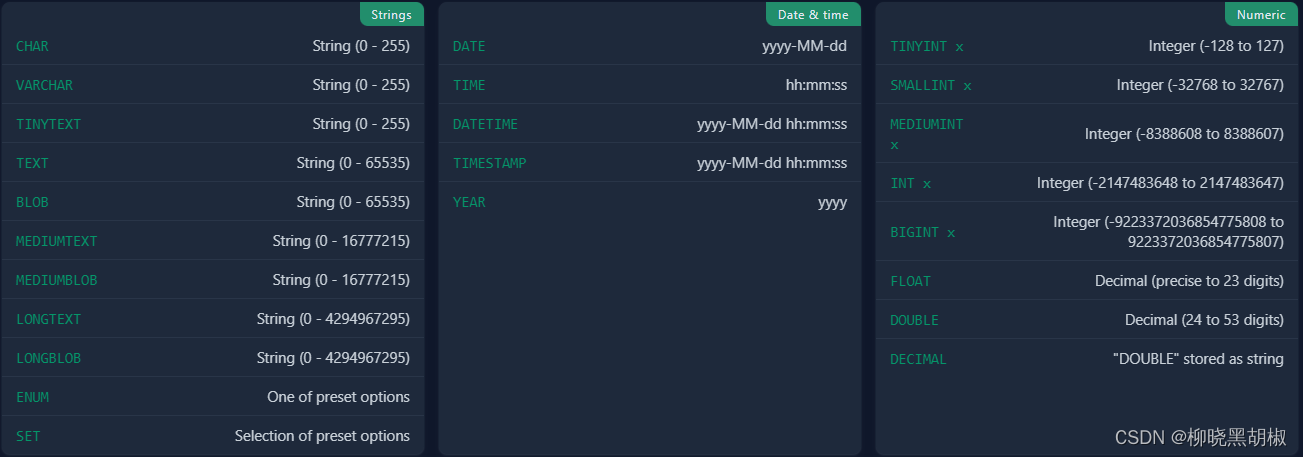
mysql 常用命令练习
管理表格从表中查询数据从多个表查询修改数据sql变量类型 管理表格 创建一个包含三列的新表 CREATE TABLE products (id INT,name VARCHAR(255) NOT NULL,price INT DEFAULT 0,PRIMARY KEY(id) // 自增 ); 从数据库中删除表 DROP TABLE product; 向表中添加新列 ALTER TAB…...

QT6 libModbus 用于ModbusTcp客户端读写服务端
虽然在以前的文章中多次描述过,那么本文使用开源库libModbus,可得到更好的性能,也可移植到各种平台。 性能:读1次和写1次约各用时2ms。 分别创建了读和写各1个连接指针,用于读100个寄存器和写100个寄存器,读写分离。 客户端&am…...
Tensor使用教程)
飞桨(PaddlePaddle)Tensor使用教程
文章目录 飞桨(PaddlePaddle)Tensor使用教程1. 安装飞桨2. 创建Tensor3. Tensor的基本属性4. Tensor的操作5. Tensor的广播机制6. Tensor与Numpy数组的转换7. 结论 飞桨(PaddlePaddle)Tensor使用教程 1. 安装飞桨 首先ÿ…...
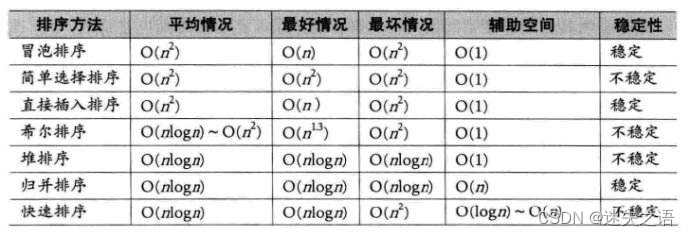
数据结构c版(3)——排序算法
本章我们来学习一下数据结构的排序算法! 目录 1.排序的概念及其运用 1.1排序的概念 1.2 常见的排序算法 2.常见排序算法的实现 2.1 插入排序 2.1.1基本思想: 2.1.2直接插入排序: 2.1.3 希尔排序( 缩小增量排序 ) 2.2 选择排序 2.2…...

《Spring Security 简易速速上手小册》第5章 高级认证技术(2024 最新版)
文章目录 5.1 OAuth2 和 OpenID Connect5.1.1 基础知识详解OAuth2OpenID Connect结合 OAuth2 和 OIDC 5.1.2 重点案例:使用 OAuth2 和 OpenID Connect 实现社交登录案例 Demo 5.1.3 拓展案例 1:访问受保护资源案例 Demo测试访问受保护资源 5.1.4 拓展案例…...

【七】【SQL】自连接
自连接初见 数据库中的自连接是一种特殊类型的SQL查询,它允许表与自身进行连接,以便查询表中与其他行相关联的行。自连接通常用于处理那些存储在同一个表中的但彼此之间具有层级或关系的数据。为了实现自连接,通常需要给表使用别名ÿ…...

C语言while 与 do...while 的区别?
一、问题 while 语句和 do...while 语句类似,都是要判断循环条件是否为真。如果为真,则执⾏循环体,否则退出循环。它们之间有什么区别呢? 二、解答 while 语句和 do..while 语句的区别在于:do..while 语句是先执⾏⼀次…...

RK3568平台开发系列讲解(基础篇)内核错误码
🚀返回专栏总目录 文章目录 一、指针的分类二、错误码三、错误码使用案例沉淀、分享、成长,让自己和他人都能有所收获!😄 一、指针的分类 二、错误码 在 Linux 内核中,所谓的错误指针已经指向了内核空间的最后一页,例如,对于一个 64 位系统来说,内核空间最后地址为 0…...
)
点云从入门到精通技术详解100篇-基于点云网络和 PSO 优化算法的手势估计(续)
目录 3 深度图像处理及转化 3.1 双目深度摄像原理及深度图的获取 3.1.1 理想化双目深度相机成像...
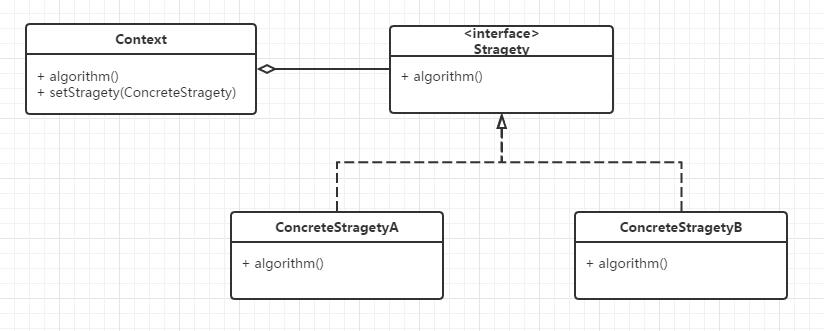
设计模式(十一)策略模式
请直接看原文:设计模式(十一)策略模式_某移动支付系统在实现账户资金转入和转出时需要进行身份验证,该系统为用户提供了-CSDN博客 ----------------------------------------------------------------------------------------------------------------…...

Java 计算某年份二月的天数
一、实验任务 要求编写一个程序,从键盘输入年份,根据输入的年份计算这一年的2月有多少天。 二、实验内容 三、实验结果 四、实现逻辑和步骤 (1)使用scanner类实现程序使用键盘录入一个年份。 (2)使用if语…...
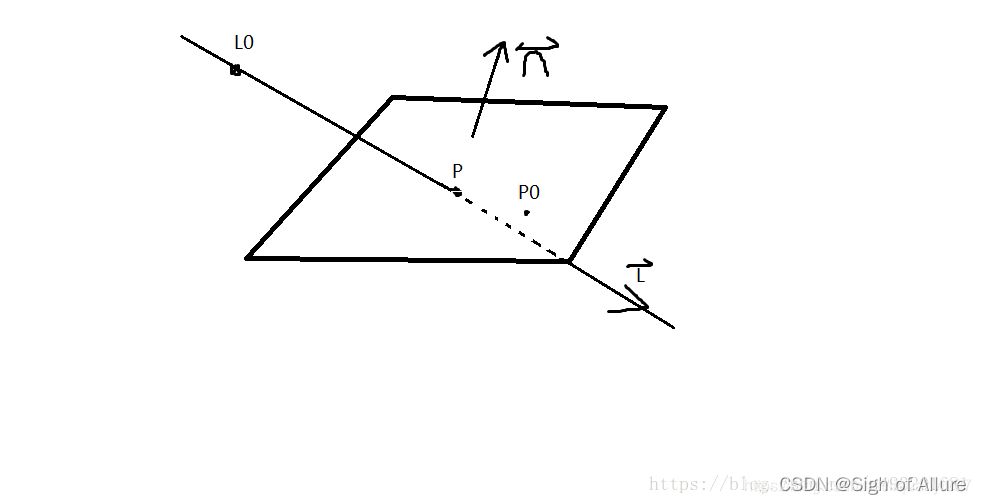
unity 数学 如何计算线和平面的交点
已知一个平面上的一点P0和法向量n,一条直线上的点L0和方向L,求该直线与该平面的交点P 如下图 首先我们要知道向量归一化点乘之后得到就是两个向量的夹角的余弦值,如果两个向量相互垂直则值是0,小于0则两个向量的夹角大于90度,大于…...

Mysql DATETIME与TIMESTAMP的区别
TIMESTAMP的取值范围小,并且TIMESTAMP类型的日期时间在存储时会将当前时区的日期时间值转换为时间标准时间值,检索时再转换回当前时区的日期时间值。 而DATETIME则只能反映出插入时当地的时区,其他时区的人查看数据必然会有误差的。 DATETI…...

hadoop基础
启动Hadoop cd /usr/local/hadoop ./sbin/start-dfs.sh #启动hadoop打开 ./bin/hdfs dfs ./bin/hdfs dfs -ls 针对 DataNode 没法启动的解决方法 cd /usr/local/hadoop ./sbin/stop-dfs.sh # 关闭 rm -r ./tmp # 删除 tmp 文件,注意这会删除 HDFS 中原有的…...

2024目前三种有效加速国内Github
大家好我是咕噜美乐蒂,很高兴又和大家见面了!截至2024年,国内访问 GitHub 的速度受到多种因素的影响,包括网络封锁、地理距离、网络带宽等。为了提高国内用户访问 GitHub 的速度,以下是目前较为有效的三种加速方式&…...
2024高频前端面试题 HTML 和 CSS 篇
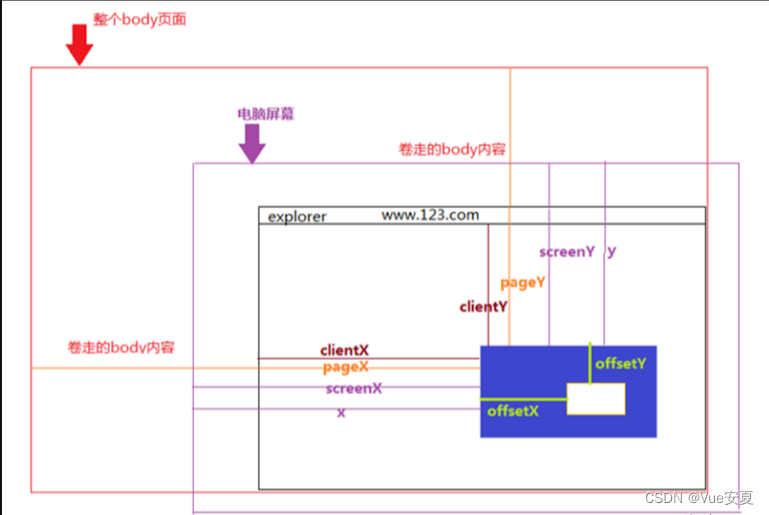
JS和ES6 篇: 2024高频前端面试题 JavaScript 和 ES6 篇-CSDN博客 一 . HTML 篇 1. H5有什么新特性 1) 语义化标签 用正确的标签做正确的事情。 html 语义化让页面的内容结构化,结构更清晰,便于对浏览器、搜索引擎解析&…...

LeetCode 100231.超过阈值的最少操作数 I
给你一个下标从 0 开始的整数数组 nums 和一个整数 k 。 一次操作中,你可以删除 nums 中的最小元素。 你需要使数组中的所有元素都大于或等于 k ,请你返回需要的 最少 操作次数。 示例 1: 输入:nums [2,11,10,1,3], k 10 输…...
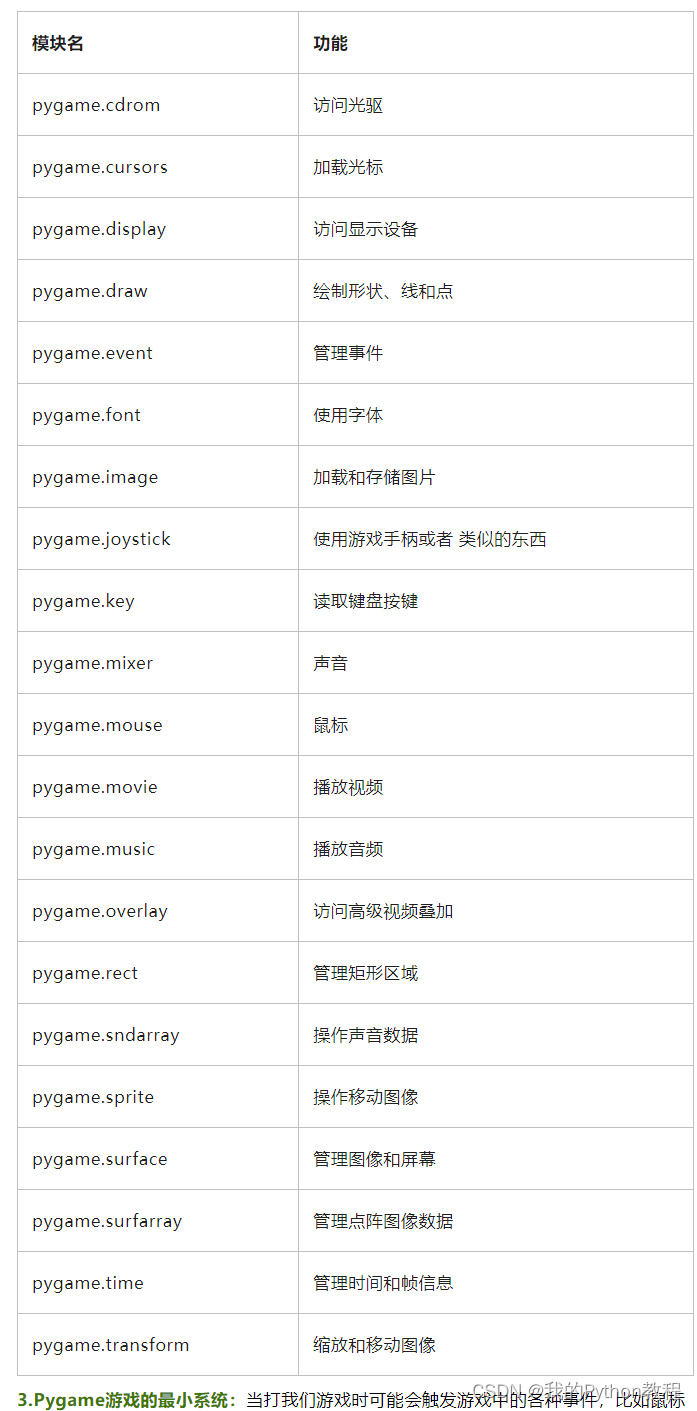
Pygame教程01:初识pygame游戏模块
Pygame是一个用于创建基本的2D游戏和图形应用程序。它提供了一套丰富的工具,让开发者能够轻松地创建游戏和其他图形应用程序。Pygame 支持许多功能,包括图像和声音处理、事件处理、碰撞检测、字体渲染等。 Pygame 是在 SDL(Simple DirectMed…...

HTML和CSS (前端共三篇)【详解】
目录 一、前端开发介绍 二、HTML入门 三、HTML基础标签 四、CSS样式修饰 五、HTML表格标签 六、HTML表单标签 一、前端开发介绍 web应用有BS和CS架构两种,其中我们主要涉及的是BS架构。而BS架构里,B(Browser浏览器)是客户端的…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...
