LeetCode 2161.根据给定数字划分数组
给你一个下标从 0 开始的整数数组 nums 和一个整数 pivot 。请你将 nums 重新排列,使得以下条件均成立:
所有小于 pivot 的元素都出现在所有大于 pivot 的元素 之前 。
所有等于 pivot 的元素都出现在小于和大于 pivot 的元素 中间 。
小于 pivot 的元素之间和大于 pivot 的元素之间的 相对顺序 不发生改变。
更正式的,考虑每一对 pi,pj ,pi 是初始时位置 i 元素的新位置,pj 是初始时位置 j 元素的新位置。对于小于 pivot 的元素,如果 i < j 且 nums[i] < pivot 和 nums[j] < pivot 都成立,那么 pi < pj 也成立。类似的,对于大于 pivot 的元素,如果 i < j 且 nums[i] > pivot 和 nums[j] > pivot 都成立,那么 pi < pj 。
请你返回重新排列 nums 数组后的结果数组。
示例 1:
输入:nums = [9,12,5,10,14,3,10], pivot = 10
输出:[9,5,3,10,10,12,14]
解释:
元素 9 ,5 和 3 小于 pivot ,所以它们在数组的最左边。
元素 12 和 14 大于 pivot ,所以它们在数组的最右边。
小于 pivot 的元素的相对位置和大于 pivot 的元素的相对位置分别为 [9, 5, 3] 和 [12, 14] ,它们在结果数组中的相对顺序需要保留。
示例 2:
输入:nums = [-3,4,3,2], pivot = 2
输出:[-3,2,4,3]
解释:
元素 -3 小于 pivot ,所以在数组的最左边。
元素 4 和 3 大于 pivot ,所以它们在数组的最右边。
小于 pivot 的元素的相对位置和大于 pivot 的元素的相对位置分别为 [-3] 和 [4, 3] ,它们在结果数组中的相对顺序需要保留。
提示:
1 <= nums.length <= 105
-106 <= nums[i] <= 106
pivot 等于 nums 中的一个元素。
法一:按顺序保存下来小于pivot和大于pivot的数,再拼接:
class Solution {
public:vector<int> pivotArray(vector<int>& nums, int pivot) {vector<int> small;vector<int> big;int pivotNum = 0;for (int num : nums){if (num < pivot){small.push_back(num);}else if (num > pivot){big.push_back(num);}else{++pivotNum;}}for (int i = 0; i < pivotNum; ++i){small.push_back(pivot);}small.insert(small.end(), big.begin(), big.end());return small;}
};
如果nums的长度为n,此算法时间复杂度为O(n),空间复杂度为O(n)。
法二:直接在结果数组中构建答案,先正向遍历nums,把小于pivot的数按顺序放在左边,然后反向遍历nums,把大于pivot的数按顺序放在右边,中间填充pivot即可:
class Solution {
public:vector<int> pivotArray(vector<int>& nums, int pivot) {vector<int> ans(nums.size());int smallIndex = 0;for (int num : nums){if (num < pivot){ans[smallIndex++] = num;}}int bigIndex = nums.size() - 1;for (vector<int>::reverse_iterator it = nums.rbegin(); it != nums.rend(); ++it){if (*it > pivot){ans[bigIndex--] = *it;}}while (smallIndex <= bigIndex){ans[smallIndex++] = pivot;ans[bigIndex--] = pivot;}return ans;}
};
如果nums的长度为n,此算法时间复杂度为O(n),空间复杂度为O(1)。本解法也可以一遍正向遍历,把大于pivot的值在ans的最后从右往左排,最后再reverse一下大于pivot的值即可:
class Solution {
public:vector<int> pivotArray(vector<int>& nums, int pivot) {vector<int> ans(nums.size(), pivot);int smallIndex = 0;int bigIndex = nums.size() - 1;for (int num : nums){if (num < pivot){ans[smallIndex++] = num;}else if (num > pivot){ans[bigIndex--] = num;}}reverse(ans.begin() + bigIndex + 1, ans.end());return ans;}
};
相关文章:

LeetCode 2161.根据给定数字划分数组
给你一个下标从 0 开始的整数数组 nums 和一个整数 pivot 。请你将 nums 重新排列,使得以下条件均成立: 所有小于 pivot 的元素都出现在所有大于 pivot 的元素 之前 。 所有等于 pivot 的元素都出现在小于和大于 pivot 的元素 中间 。 小于 pivot 的元素…...

ip获取+归属地实现
1.背景 现在的社交平台一般都需要展示用户的归属地,这个功能有下面二个主要功能点,接下来我们来介绍下具体实现。 IP 获取 IP 转归属地 2.ip获取 2.1 Http请求 对于controller的请求,我们只需要写个拦截器,将用户的ip设置进上下文即可,非常方便。 @Override public bo…...

Python的错误和异常
文章目录 python的语法错误异常异常处理用户自定义异常定义清理行为预定义的清理行为 python的语法错误 语法错误(Syntax Error)是指代码不符合Python语言的语法规则。当解释器在执行代码之前对其进行解析时,如果发现代码中有语法错误&#…...

C语言-------指针进阶(2)
1.指针数组 指针数组表较简单,类比整型数组,字符数组,整型数组里面的元素都是整型变量,字符数组里面 的元素是字符类型,那么指针数组就是数组里面的每个元素都是指针类型,例如int*arr[5]就是一个 指针数…...

Spring El表达式官方文档学习
文章目录 推荐一、概述1、什么是SpEL2、SpEL能做什么 二、SpEL表达式使用1、文字表达式2、属性, 数组, List, Map,和 索引(1)属性操作(2)数组和List(3)Map 3、内嵌List4、内嵌Map5、构建数组6、调用类的方法…...
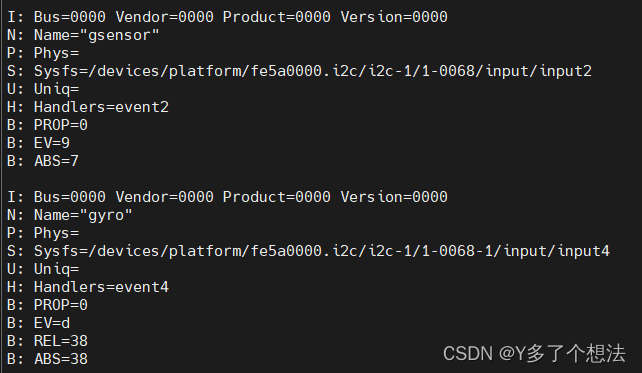
RK3568 android11 调试陀螺仪模块 MPU6500
一,MPU6500功能介绍 1.简介 MPU6500是一款由TDK生产的运动/惯性传感器,属于惯性测量设备(IMU)的一种。MPU6500集成了3轴加速度计、3轴陀螺仪和一个板载数字运动处理器(DMP),能够提供6轴的运动…...
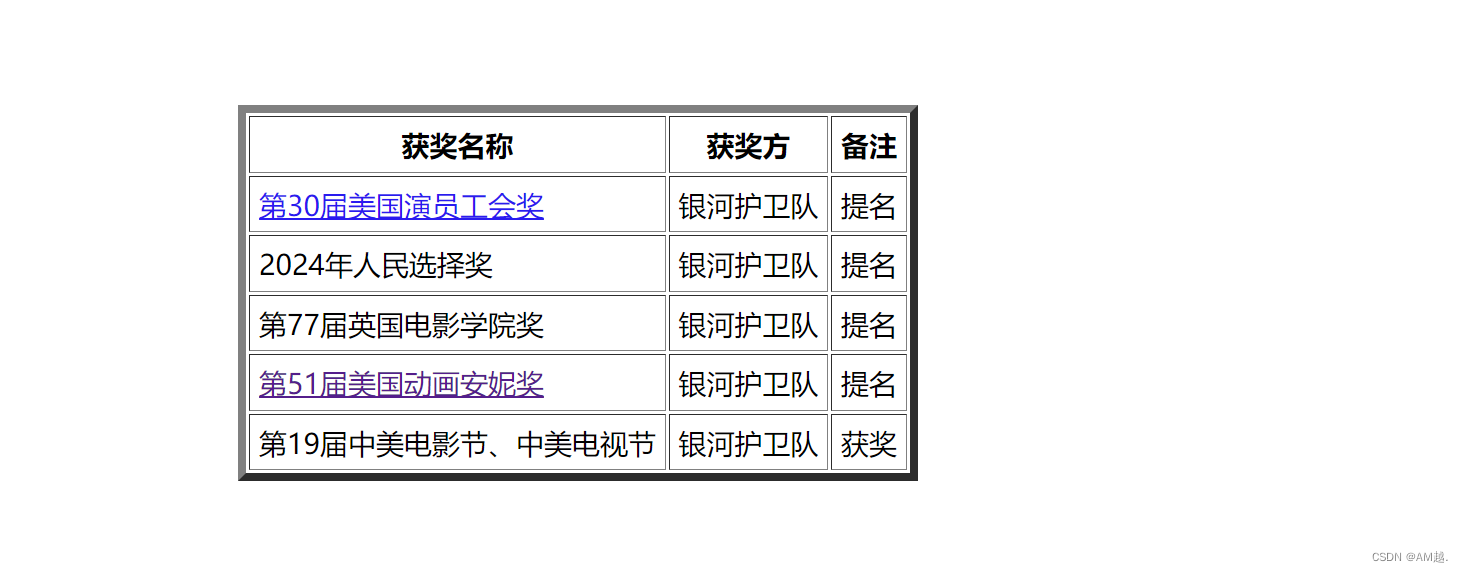
【HTML】HTML基础6.1(表格以及常见属性)
目录 表格介绍 表格标签 表格标签的常见属性 案例 知识点总结 表格介绍 在浏览器中,我们经常见到形如 这样的表格形式,一般来说,表格是为了让数据看起来更加清晰,增强数据的可读性 有的程序员也会用表格进行排版 表格标签 &…...

数字电路三宝:锁存器、寄存器和触发器
在数字电路设计中,很多电子工程师经常会用到锁存器、寄存器和触发器,它们各自承担着不同的功能,但共同为数字电路的稳定性和高效性提供了坚强保障,下面将谈谈这三大元件,希望对小伙伴们有所帮助。 1、锁存器࿰…...

VLC相关资源及使用方法
资源 VLC源码: VLC的源码,与VLC Contrib配合使用可以编译相应的库、程序等,如果没有Contrib,可以使用源码下面的contrib文件夹下对应程序自动下载,单独编译,但是速度很慢。 下载地址: 官网&…...
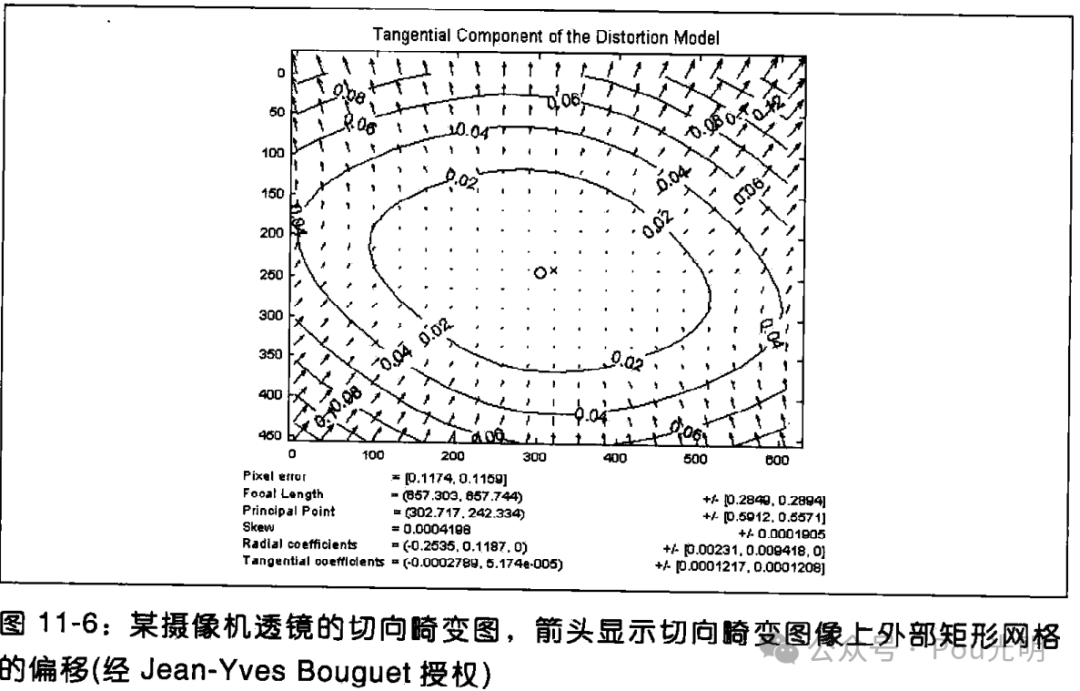
4_相机透镜畸变
理论上讲,是可能定义一种透镜而不引入任何畸变的。然而现实世界没有完美的透镜。这主要是制造上的原因,因为制作一个“球形”透镜比制作一个数学上理想的透镜更容易。而且从机械方面也很难把透镜和成像仪保持平行。下面主要描述两种主要的透镜畸变并为他…...
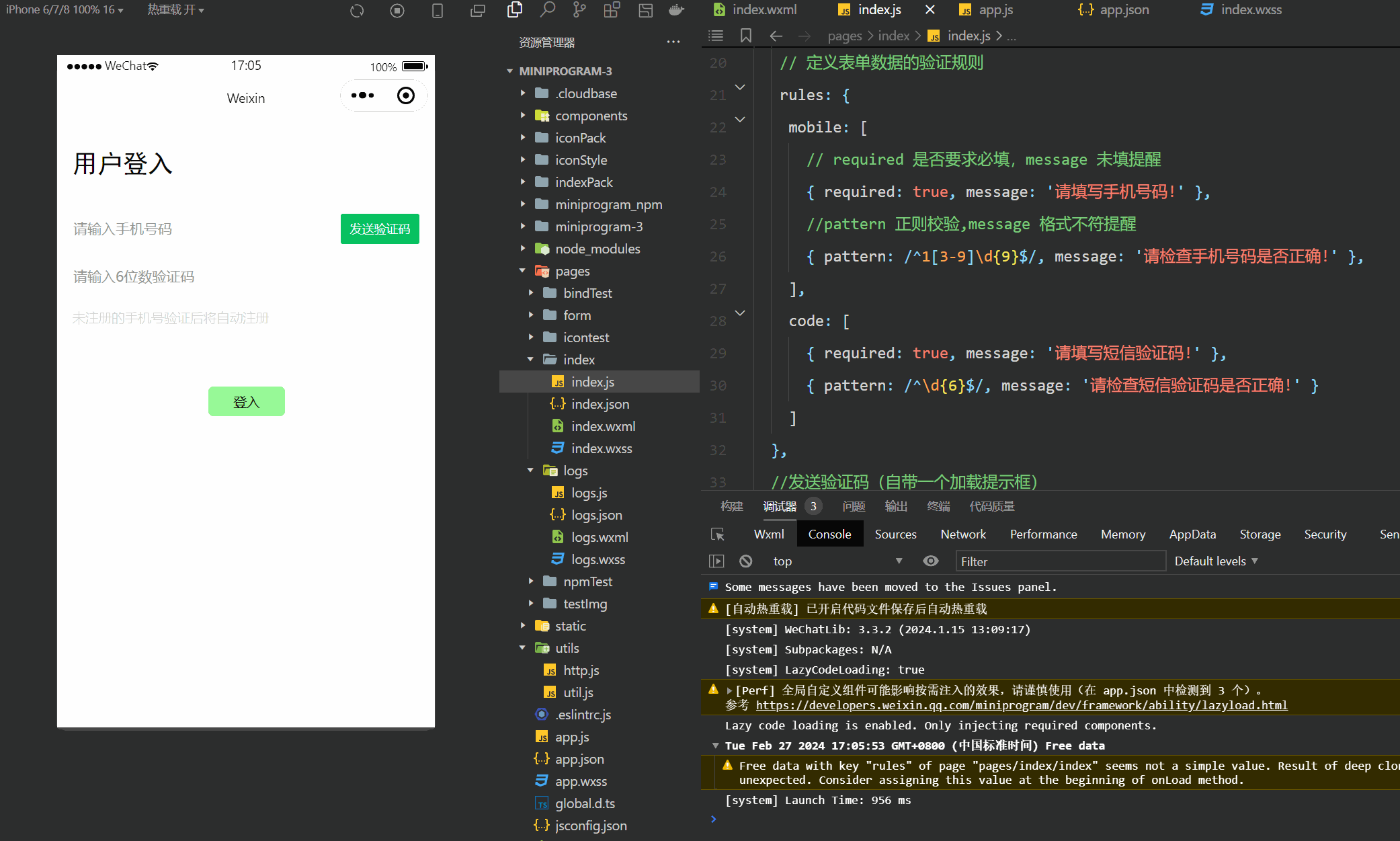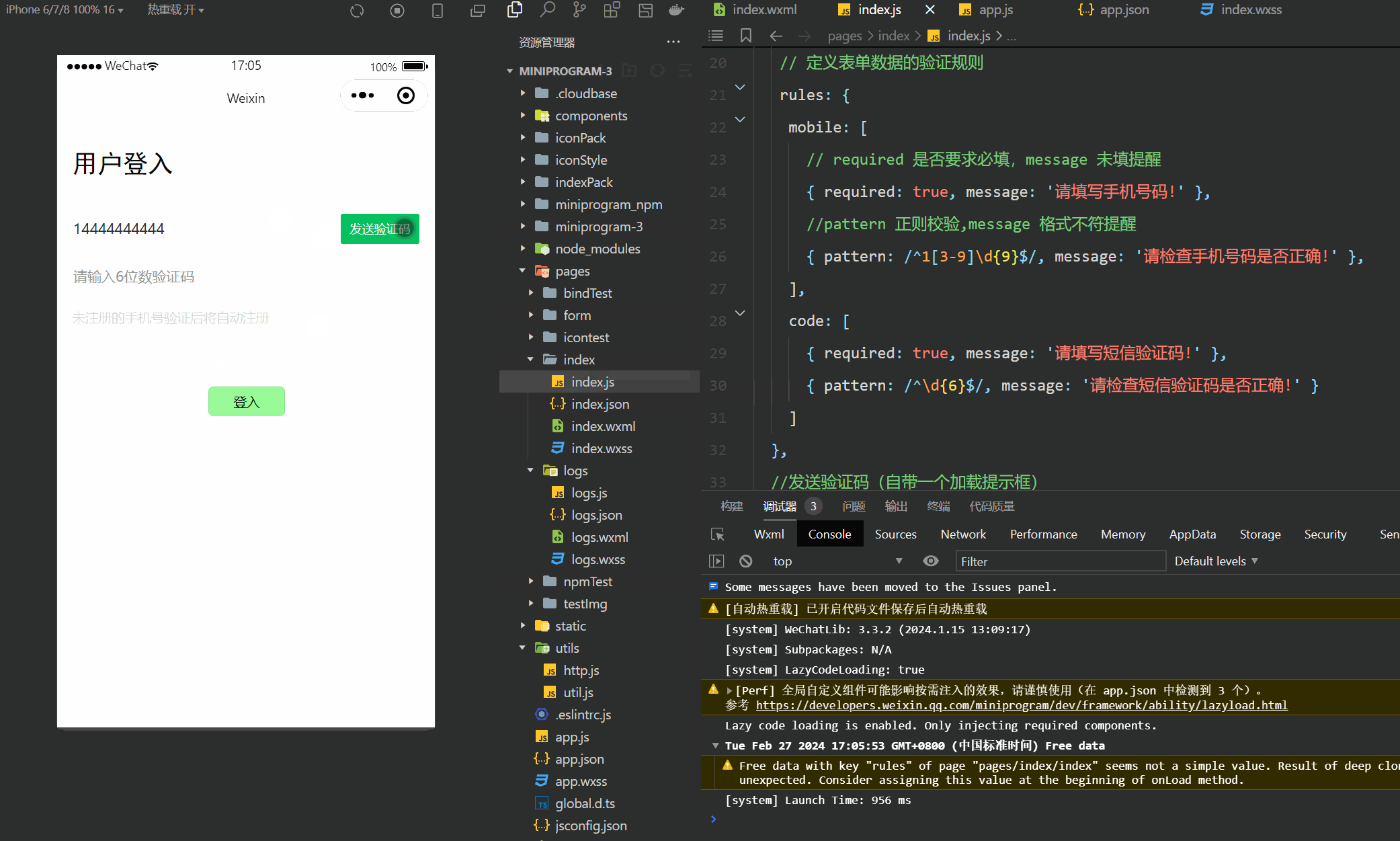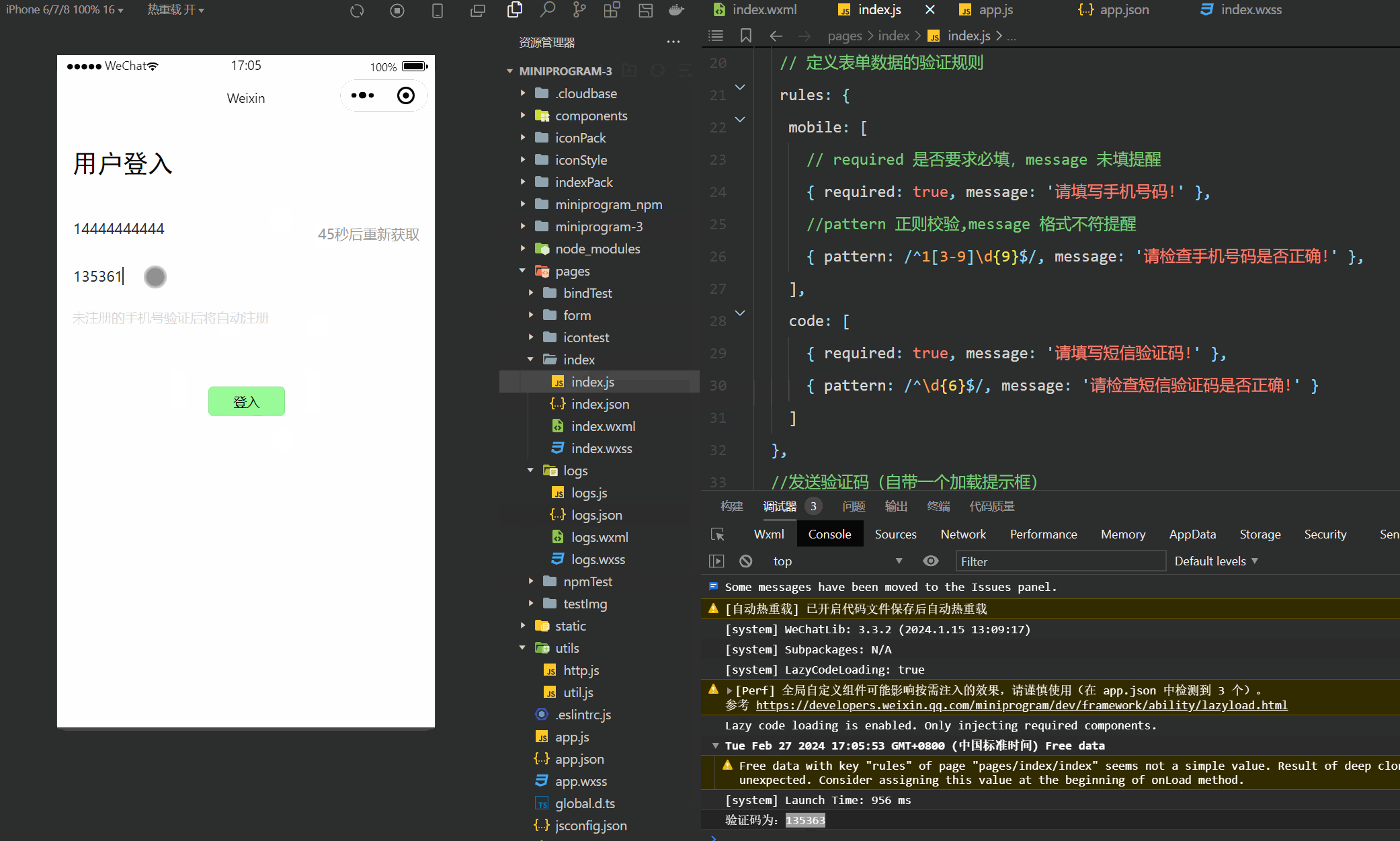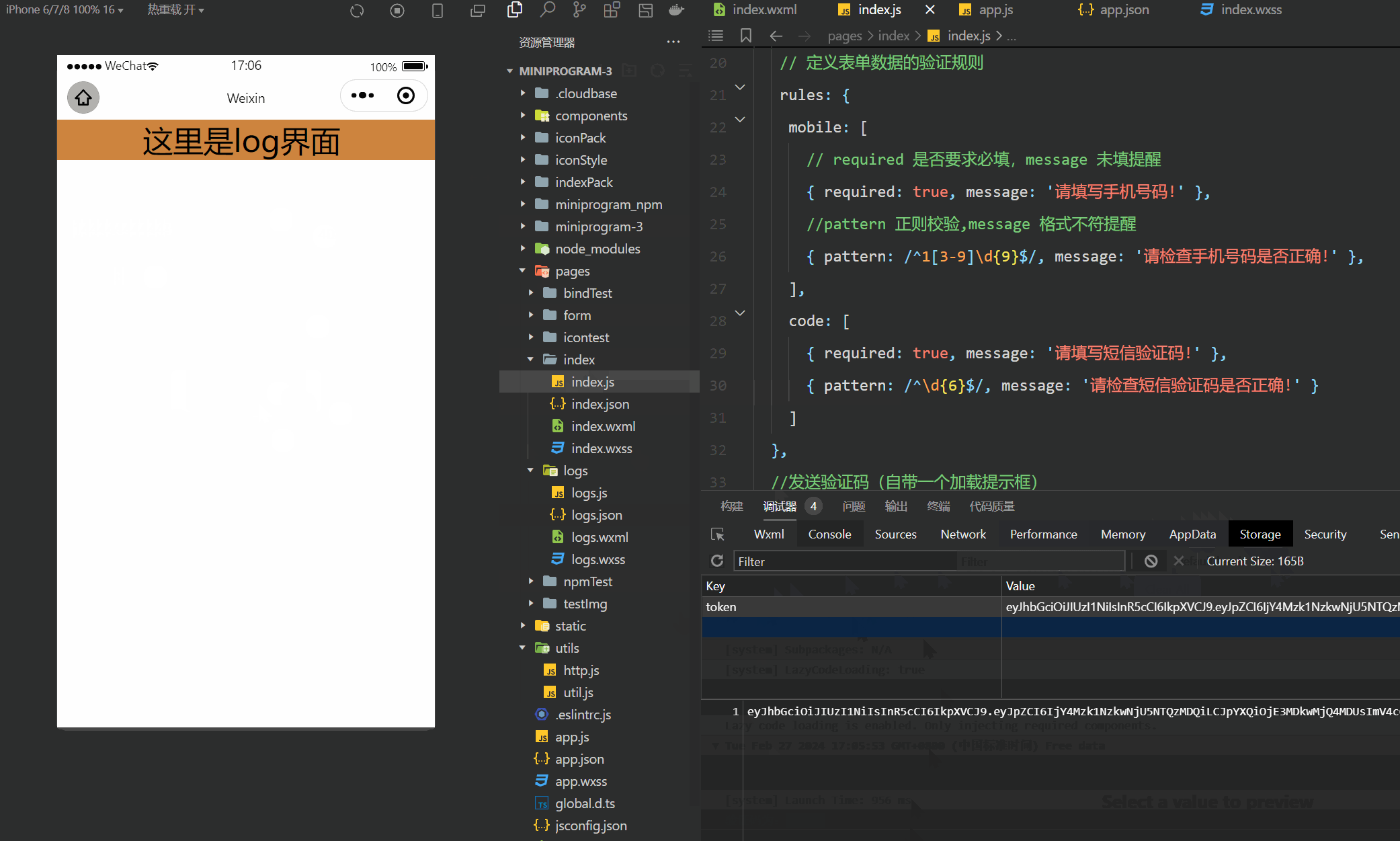
微信小程序(四十六)登入界面-进阶版
注释很详细,直接上代码 上一篇 此文使用了vant组件库,没有安装配置的可以参考此篇vant组件的安装与配置 新增内容: 1.手机号与验证码格式验证 2.验证码的网络申请和校验 wechat-http模块在好几篇以前已经讲了咋安装的,不记得的友…...

CSP-201712-2-游戏
CSP-201712-2-游戏 解题思路 初始化变量:定义整数变量n和k,分别用来存储小朋友的总数和淘汰的特定数字。然后定义了num(用来记录当前报的数)和peopleIndex(用来记录当前报数的小朋友的索引)。 初始化小朋…...

记录SSM项目集成Spring Security 4.X版本 之 加密验证和记住我功能
目录 前言 一、用户登录密码加密认证 二、记住我功能 前言 本次笔记的记录是接SSM项目集成Spring Security 4.X版本 之 加入DWZ,J-UI框架实现登录和主页菜单显示-CSDN博客https://blog.csdn.net/u011529483/article/details/136255768?spm1001.2014.3001.5502 文章之后补…...

[AutoSar]BSW_Com09 CAN driver 模块FULL(BASIC)CAN、FIFO选择
目录 关键词平台说明一、FULL CAN 和Basic CAN 关键词 嵌入式、C语言、autosar、OS、BSW 平台说明 项目ValueOSautosar OSautosar厂商vector ,芯片厂商TI 英飞凌编程语言C,C编译器HighTec (GCC)autosar版本4.3.1 >>>>>回到总目录<&…...

WPF真入门教程30--顺风物流单据管理系统
1、教程回顾 到现在为止,真入门系列教程已完成了29刺由浅入深地讲解,当然不可能讲到了WPF的所有技能点,但读者看到了wpf的内部各种功能及之间的联系,在此基础上,提供一个完整有效的综合项目,本项目采用的是…...
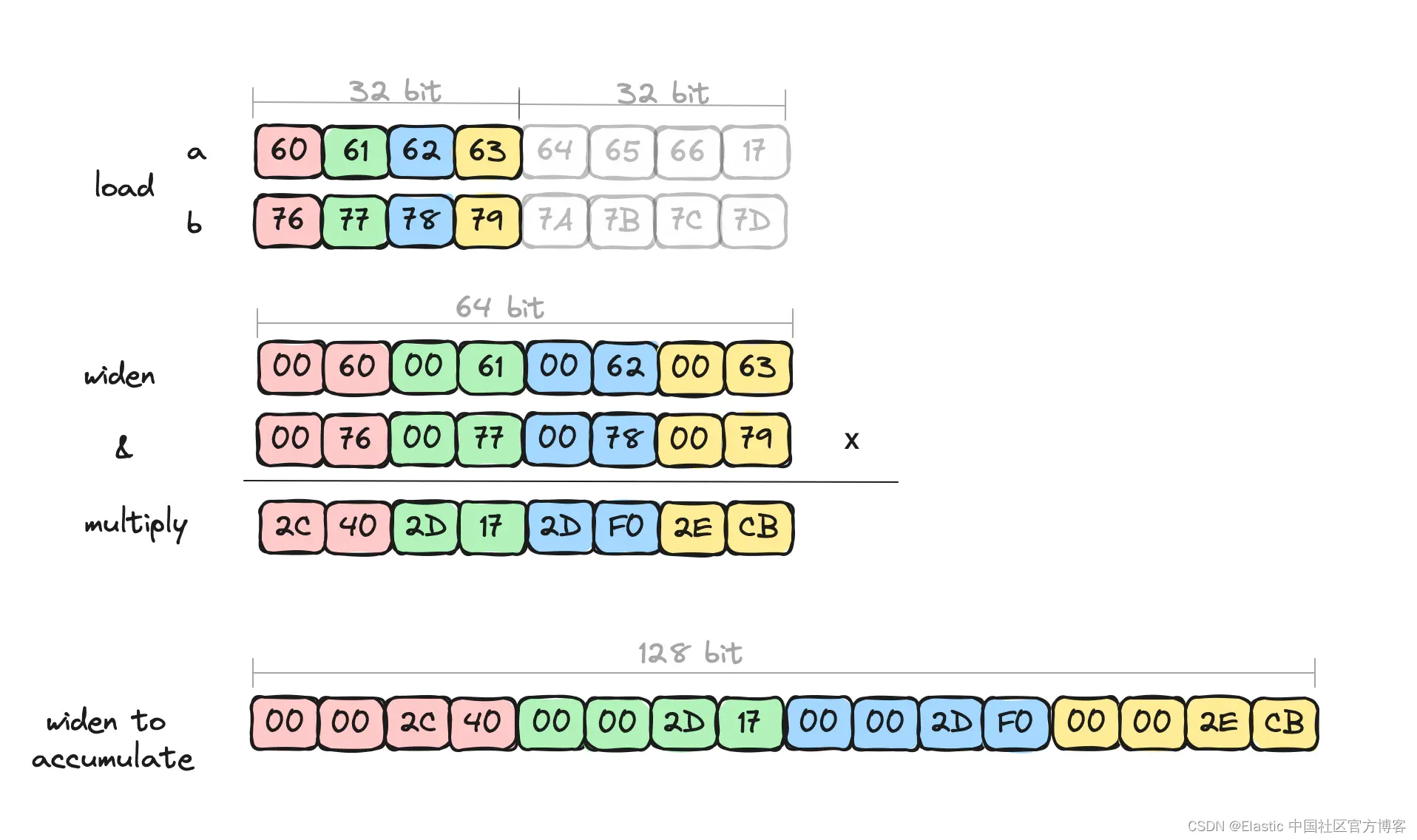
Elasticsearch:向量相似度计算 - 可笑的速度
作者:Chris Hegarty 任何向量数据库的核心都是距离函数,它确定两个向量的接近程度。 这些距离函数在索引和搜索期间执行多次。 当合并段或在图表中导航最近邻居时,大部分执行时间都花在比较向量的相似性上。 对这些距离函数进行微观优化是值…...

两数相加的问题
题目是:给两个非空的链表,表示两个非负整数。它们每位数都是按照逆序的方式存储,并且每一个节点只能存储一位数字。现在两个数相加,并且以相同的形式返回一个表示和的链表。 首先回顾一下,什么是链表?链表…...

微信小程序的单位
在小程序开发中,rpx是一种相对长度单位,用于在不同设备上实现自适应布局。它是微信小程序特有的单位,表示屏幕宽度的 1/750。 rpx单位的好处在于可以根据设备的屏幕宽度进行自动换算,使得页面在不同设备上保持一致的显示效果。例…...

软考通过率真的低吗?
软考通过率有多少?高项有必要找培训机构吗? 相对来说软考的通过率的确比其他考试要低,因为它的知识点有点杂,专业知识、政策、计算机系统各个方面的知识都需要去掌握。根据以往的数据来说高项(信息系统项目管理师&…...

国际视频编解码标准提案下载地址
H.266 相关提案下载地址:http://phenix.it-sudparis.eu/jvet/ 更新的地址:https://jvet-experts.org/ H.265 提案下载地址:http://phenix.int-evry.fr/jct/ 标准文档下载地址:http://www.itu.int/rec/T-REC-H.265 H.264 提案下载…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...
