分享经典、现代和前沿软件工程课程
随着信息技术的发展,软件已经深入到人类社会生产和生活的各个方面。软件工程是将工程化的方法运用到软件的开发、运行和维护之中,以达到提高软件质量,降低开发成本的目的。软件工程已经成为当今最活跃、最热门的学科之一。
本次软件工程MOOC课程是一门导论性课程,我们将全面介绍软件工程所涉及的各方面知识,包括软件过程、软件需求、结构化分析和设计方法、面向对象分析和设计方法、敏捷开发方法、软件测试、软件项目管理、软件开发工具和环境。通过课程讲授,让大家初步了解软件开发和维护的方法学,为进一步深入学习各专题打下基础。
软件工程的目的是以工程的原理、原则和方法进行软件开发,以解决软件危机。所以软件工程的总目标不是寻求最优解。而系统工程的目标是寻求最优解。但软件开发中的软件需求分析、软件体系结构设计、软件的集成测试和软件的系统测试等活动,已经可以看作软件系统工程的工程活动。
希望软件工程未来能真正发展到像目前制造业那样流水线生产组装制造软件的模式,但即使到这一步,由于用户需求的千差万别,定制化应用也是需要的。我个人认为,定制化应用开发中,会复用一些满足部分需求的软件构件,同时还要开发一些新需求的软件构件,然后组装集成为最终的定制化应用。做产品设计需要考虑低耦合的功能,只有这样,产品本身以及构成产品的软件构件才能有更长的生命周期。
课程还包含了实践环节,通过一个小型软件项目,大家可以体验软件开发的各个环节,并形成项目管理的意识。帮助读者系统而完整地梳理了软件工程的经典、现代和前沿理论、方法和技术,通过案例分析让读者了解其运用,并以浅显易懂的方式讲授业界广泛使用的方法和技术如敏捷开发方法、群智化开发方法-开源和众包、DevOps方法等,让读者理解和掌握现代业界使用的方法和技术。而且,作者结合北京大学和浙江大学在软件工程前沿的研究成果,首次在国内外软件工程教材中,系统化地介绍了人工智能(AI)、区块链(Blockchain)、云计算(Cloud Computing)、大数据(Big Data)、物联网(IoT)等新型技术驱动的前沿软件工程理论和方法,以此拓展读者的软件工程视野。
“人月神话”的意思,是指在软件开发过程中,人们往往以“人月”作为估计工作量的单位,并认为通过增加人手就能以同等比例缩短所需的开发时间,比如说10个人预计10个月的开发工作量,100个人应该可以在一个月内完成。这种想当然的意见往往与事实天差地别,因此被称为“神话”。
“人月神话”不能成立的原因,一是`当任务由于次序上的限制不能分解时,人手的添加对进度没有帮助。`二是`对于可以分解,但子任务之间需要相互沟通和交流的任务,必须在计划工作中考虑沟通的工作量。`
理论上说,一对一的情况下,三个人之间的沟通量是两个人之间沟通量的3倍,四个人之间的沟通量是两个人之间沟通量的6倍,考虑到多个人或者多个团队之间开会协商、一起解决问题的需要,增加人手的作用往往要大打折扣,甚至可能起到负面的作用。
以尽量精简的团队完成任务当然是最佳选择。但小团队毕竟无法承担大型软件开发任务,因为软件开发有其时效性,再高的效率,以大型软件的工作量计,也要十数年才能完成开发——这在商业上是没有意义的。
因此,就展开了本书讨论的主题:如何管理大型软件项目开发。
主教材
孙艳春, 黄罡, 邓水光. 软件工程:经典、现代和前沿.
北京大学出版社,2024.2, ISBN 978-7-301-34801-7.

软件工程_北京大学_中国大学MOOC(慕课)
北京大学出版社
北京大学-软件工程(国家级精品课)课堂录播–孙艳春老师_哔哩哔哩_bilibili
爱课程 软件工程 北京大学信息科学技术学院
人月神话(纪念典藏版)【美】小弗雷德里克·P.布鲁克斯 清华大学出版社


相关文章:

分享经典、现代和前沿软件工程课程
随着信息技术的发展,软件已经深入到人类社会生产和生活的各个方面。软件工程是将工程化的方法运用到软件的开发、运行和维护之中,以达到提高软件质量,降低开发成本的目的。软件工程已经成为当今最活跃、最热门的学科之一。 本次软件工程MOOC课…...
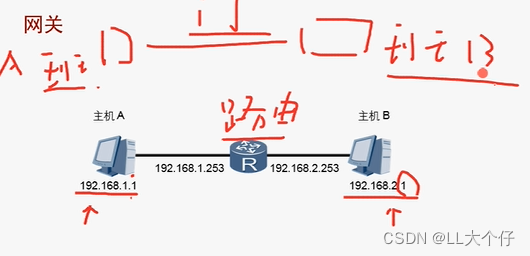
网络工程师笔记3
IP地址类型 A类 255.0.0.0B类 255.255.0.0C类 255.255.255.0D类 E类 子网掩码:从左到右连续的确定网络位 2-4-8-16-32-64-128-256 128 : 1000 0000 64 : 0100 0000 32 : 0010 0000 16 : 0001 0000 8 &am…...

【菜鸟入门!】Matlab零基础快速入门教程
数学建模竞赛中,编程软件是必不可缺少的,比如大家都熟知的MATLAB多数同学们都会经常用到,今天给大家介绍一些MATLAB的基本元素,希望帮助大家更好的掌握编写基本的函数! 变量和数组 MATLAB 程序的基本数据单元是数组。一…...
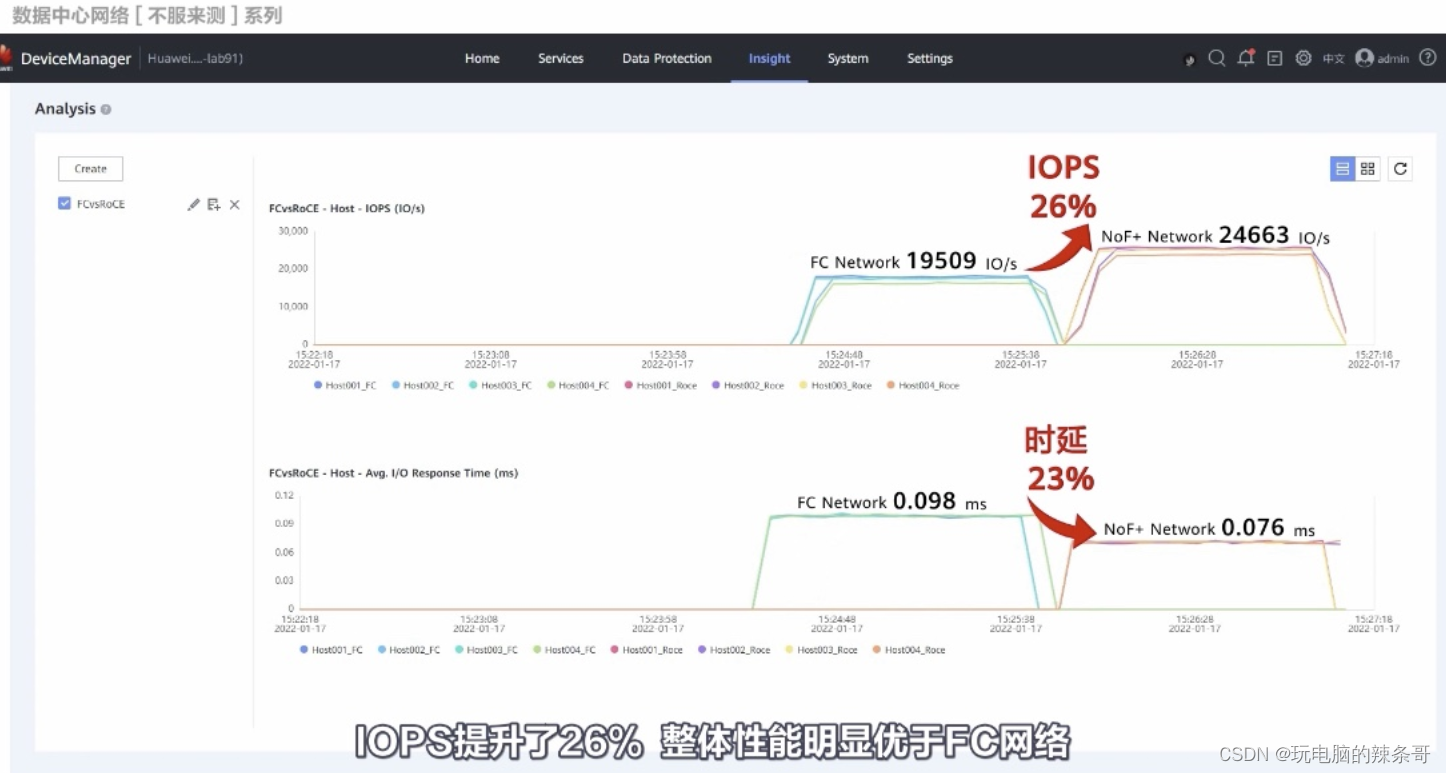
数据中心GPU集群高性能组网技术分析
数据中心GPU集群组网技术是指将多个GPU设备连接在一起,形成一个高性能计算的集群系统。通过集群组网技术,可以实现多个GPU设备之间的协同计算,提供更大规模的计算能力,适用于需要大规模并行计算的应用场景。 常用的组网技术&…...

go垃圾回收
1 go 垃圾回收变更 Go 语言的垃圾回收器(GC)自其诞生以来一直在不断演进和优化,以提高性能、减少暂停时间和对程序执行的影响。以下是一些关键的改进和变更点: 并发标记周期: Go 语言从一开始就采用了并发标记…...

如何做代币分析:以 LEO 币为例
作者: lesleyfootprint.network 编译:cicifootprint.network 数据源:LEO 代币仪表板 (仅包括以太坊数据) 在加密货币和数字资产领域,代币分析起着至关重要的作用。代币分析指的是深入研究与代币相关的数…...

数制和码制
目录 几种常见的数制 数制 基数 位权 常见的四种数制 十进制数 二进制数 八进制数 十六进制数 不同进制数的相互转换 例如 例如 编码 二-十进制码 例如 格雷码 例如 原码、反码和补码 几种常见的数制 关键术语 数制:以一组固定的符号和统一的规则来表示数值…...

Git Bash中安装tree
文章目录 问题描述解决办法A备选办法BRef 问题描述 在Git Bash中使用tree报错: tree # bash: tree: command not found解决办法A 下载二进制文件: https://gnuwin32.sourceforge.net/packages/tree.htm -> 选binary。下载后解压.zip 把解压后的tre…...
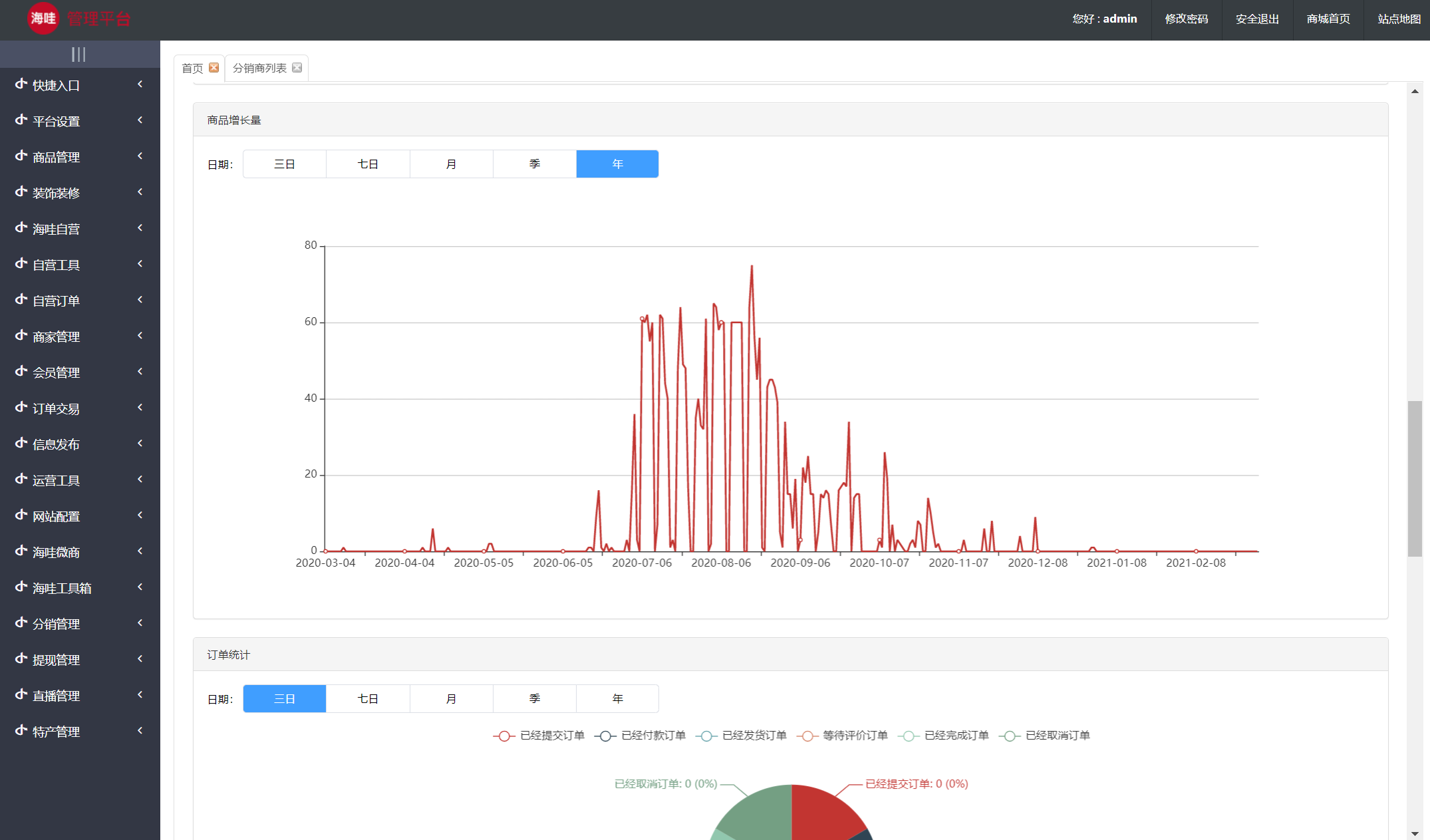
java开源 VR全景商城 saas商城 b2b2c商城 o2o商城 积分商城 秒杀商城 拼团商城 分销商城 短视频商城 小程序商城搭建
1. 涉及平台 平台管理、商家端(PC端、手机端)、买家平台(H5/公众号、小程序、APP端(IOS/Android)、微服务平台(业务服务) 2. 核心架构 Spring Cloud、Spring Boot、Mybatis、Redis 3. 前端框架…...

C++练手题系列一
第 1 题 【 问答题 】 • 有多少种二叉树 输入n(1<n<13),求n个结点的二叉树有多少种形态 时间限制:1000 内存限制:65536 输入 整数n 输出答案 样例输入 3 样例输出 5 第 2 题 【 问答题 】 • 城堡问题 1 2 3 4 5 6 7 ################…...
async/await高级用法,你会多少种呢?)
(下)async/await高级用法,你会多少种呢?
公众号:程序员白特,欢迎一起交流学习~ 前言 众所周知,在 ECMA17 中加入了两个关键字 async、await,简单来说它们是基于 Promise 之上的语法糖,可以让异步操作更加简洁明了。在掌握async、await的基础用法后࿰…...

阅读笔记 | REFORMER: THE EFFICIENT TRANSFORMER
阅读论文: Kitaev, Nikita, Łukasz Kaiser, and Anselm Levskaya. “Reformer: The efficient transformer.” arXiv preprint arXiv:2001.04451 (2020). 背景与动机 这篇论文发表较早,主要关注Transformer的效率问题。标准的Transformer模型在许多自然…...

光路科技:工业以太网交换机引领工业互联网新篇章
随着全球范围内工业4.0的浪潮不断涌动,工业互联网作为其核心驱动力,正引领着工业生产向智能化、网络化的崭新阶段迈进。在这一转型的浪潮中,光路科技凭借其卓越的工业互联设备与创新解决方案,正为工业互联网领域的发展注入新的活力…...

航拍无人机技术,航拍无人机方案详解,无人机摄影技术
航拍无人机是利用遥控技术和摄像设备,在空中进行拍摄和录像的无人机。这种无人机通常具有高清摄像设备、图像传输设备、GPS定位系统、智能控制系统等,可以轻松实现各种拍摄角度和高度,广泛应用于影视制作、旅游景区航拍、城市规划、环保监测等…...
【ArcPy】游标访问几何数据
访问质心坐标相关数据 结果展示 代码 import arcpy shppath r"C:\Users\admin\Desktop\excelfile\a2.shp" with arcpy.da.SearchCursor(shppath, ["SHAPE","SHAPEXY","SHAPETRUECENTROID","SHAPEX","SHAPEY",&q…...

Java云计算k8s
云计算k8s k8s简介容器技术的发展使用kubeadm安装k8skubectlKubernetes 架构k8s节点节点与控制面之间的通信控制器k8s kubectl命令详解k8s容器Kubernetes 对象Kubernetes 对象管理Kubernetes 对象管理 指令式命令Kubernetes 对象管理 指令式对象配置k8s对象管理 声明式对象配置…...
蜂窝物联:物联网大数据云平台功能模块简介
蜂窝云平台可远程获取现场环境(如温室大棚、稻田)的空气温湿度、土壤水分温度、二氧化碳浓度、光照强度及视频图像,通过数据模型分析,可以自动控制湿帘、风机、喷淋滴灌、内外遮阳、顶窗侧窗、加温补光、增氧机等设备;…...

Docker镜像导出/导入
Docker镜像导出/导入 一、前言 在实际操作中,为了便于docker镜像环境和服务配置的迁移,我们有时需要将已在测试环境主机上完成一系列配置的docker镜像或运行中的容器镜像导出,并传输到生产或其他目标环境主机上运行。为此,本文主…...

SwiftUI 如何在运行时从底层动态获取任何 NSObject 对象实例
概览 众所周知,SwiftUI 的推出极大地方便了我们这些秃头码农们搭建 App 界面。不过,有时我们仍然需要和底层的 UIKit 对象打交道。比如:用 SwiftUI 未暴露出对象的接口改变视图的行为或外观。 从上图可以看到,我们 SwiftUI 代码并没有设置视图的背景色,那么它是怎么变成绿…...

LeetCode 2161.根据给定数字划分数组
给你一个下标从 0 开始的整数数组 nums 和一个整数 pivot 。请你将 nums 重新排列,使得以下条件均成立: 所有小于 pivot 的元素都出现在所有大于 pivot 的元素 之前 。 所有等于 pivot 的元素都出现在小于和大于 pivot 的元素 中间 。 小于 pivot 的元素…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...
