数制和码制
目录
几种常见的数制
数制
基数
位权
常见的四种数制
十进制数
二进制数
八进制数
十六进制数
不同进制数的相互转换
例如
例如
编码
二-十进制码
例如
格雷码
例如
原码、反码和补码
几种常见的数制
关键术语
数制：以一组固定的符号和统一的规则来表示数值的方法
进位计数制：按一定数值大小进位计数，表示数的方式
数制
任何一种进位计数制包含两个基本的要素：基数和位权
基数
基数是进位计数制中所采用数码的个数
如果是R进制计数，进位规则是"逢R进一"，则要有R个数码，R就是进制计数的基数
例如，十进制计数，有0、1、2、…、9十个不同的数码，基数R为10，六进制计数，有0、1、2、…、5六个不同的数码，基数R为6
位权
在表征数的大小时，由不同的数码组合排列表示，处在不同数位的数码，代表不同的数值，每一个数位的数值大小由该位数码的值乘以处于该位的一个固定值，这个固定值就是该位的“权值”，称为“位权”
如十进制数456的值为4×100+5×10+6×1，其中最高位数码代表数值400，十位上的数码代表数值是50，最低位数码代表数值是6
常见的四种数制
十进制数
基数R=10的数制称为十进制，有0、1、2、3、4、5、6、7、8、9十个数码，计数规则为“逢十进一”和“借一当十”
二进制数
基数R=2的数制称为二进制，有0、1两个数码，对于相邻两位来说，高位的权值是低位权值的2倍，计数时为“逢二进一”和“借一当二”
八进制数
基数R=8的数制称为八进制，有0、1、2、3、4、5、6、7八个数码，对于相邻两位来说，高位的权值是低位权值的8倍，计数时为“逢八进一”和“借一当八”
十六进制数
基数R=16的数制称为十六进制，有0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F十六个数码，其中A、B、C、D、E、F分别代表10、11、12、13、14、15，对于相邻两位来说，高位的权值是低位权值的16倍，计数时为“逢十六进一”和“借一当十六”
常见四种进位计数制之间的对照表 十进制 二进制 八进制 十六进制 0 0000 0 0 1 0001 1 1 2 0010 2 2
3 0011 3 3 4 0100 4 4 5 0101 5 5 6 0110 6 6 7 0111 7 7 8 1000 10 8 9 1001 11 9 10 1010 12 A 11 1011 13 B 12 1100 14 C 13 1101 15 D 14 1110 16 E 15 1111 17 F
不同进制数的相互转换
同一个数，可以用不同的进位计数制表示，所以，不同数制间的转换，其实质就是不同数制间的基数转换，转换的原则为：如果两个有理数相等，则两个数的整数和小数部分分别相等
R进制转换成十进制数的方法为：将被转换的数按权展开
例如
1.将二进制数1010.11转换成十进制数
2.将八进制数27.2转换成十进制数
3.将十六进制A6.4转换成十进制数
解：对于第一题
以下数都为十进制
1 0 1 0 . 1 1 第三位 第二位 第二位 第一位 小数点后第一位 小数点后第二位 2^3 2^2 2^1 2^0 2^-1 2^-2 1*2^3+0*2^2+1*2^1+0*2^0+1*2^-1+1*2^-2=8+2+0.5+0.25=10.75
对于第二题
2 7 . 2 第二位 第一位 小数点后第一位 8^1 8^0 8^-1 以下数都为十进制
2*8^1+7*8^0+2*8^-1=16+7+0.25=23.25
对于第三位
A 6 . 4 第二位 第一位 小数点后第一位 16^1 16^0 16^-1 以下数都为十进制
10*16^1+6*16^0+4*16^-1=160+6+0.25=166.25
十进制数转化成R进制数
十进制数转换成R进制数时，整数部分和小数部分需要分别进行转换
对于整数部分，除R取余法，逆序排列，其中R为基数对于小数部分，乘R取整法，顺序排列
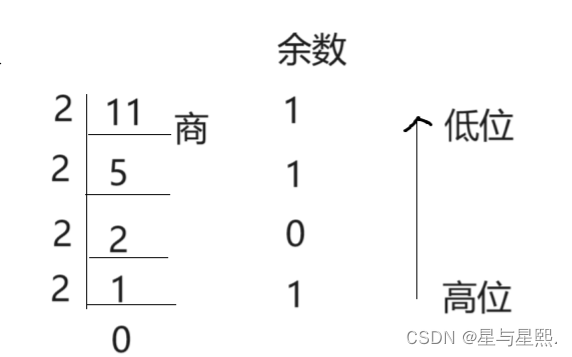
例如十进制11.375转换成相应的二进制数
解：整数转换:采用除2取余法(R=2)
11的十进制=1011的二进制
小数转换：采用乘2取整数(R=2)，运算时，式中的整数不参加连乘
0.375的十进制=0.011的二进制
所以
11.375的十进制=1011.011的二进制
编码
关键术语
编码：按一定的方式将0、1数码进行编排，使其表示特定的信息
一般，如有N个特定信息需代码表示，则所需的二进制代码位数n(称为码长)与N项信息之间应当满足2^n≥N
二-十进制码
用4位二进制数表示1位十进制数的代码，称为二-十进制码，又称BCD码，其有很多种不同的编码方式其特征分为有权码和无权码两种类型
8421BCD码
该代码的编码方式为：选择4位自热二进制数的前10组代码，对其0~9进行编码。在一组代码中，每一位二值代表一个固定数值，即有一定的权值，如果将每一位的1所代表的权值按十进制数加起来，其结果是该代码所表示的十进制数，代码从左到右每一位的权值分别为8、4、2、1，这种代码称为8421BCD码，它属于有权码
2421BCD码2421BCD码是一种有权码，代码中从左到右每一位的权值分别为2、4、2、1，其中代码特点为0和9，1和8，2和7，3和6，4和5互为反码，该特性称为互补性，2421BCD码的编码方案有多种，如十进制数的4，可以有0100和1010两种编码
5211BCD码5211BCD码是一种有权码，代码从左到右每一位的权值分别为5、2、1、1，5211BCD码的编码方案也有多种，如十进制数的3，有0110和0101两种编码
例如
将698.54十进制转换成8421BCD码
即十进制的每一位由8421BCD码代替
一位用四位表示
6对应0110
9对应1001
8对应1000
5对应0101
4对应0100
698.54的十进制=0110 1001 1000 . 0101 0100 8421BCD码
将76十进制转换成8421BCD码7对应0111
6对应0110
76的十进制=0111 0110 8421BCD码
将76.34转换成1215BCD码7对应1011
6对应0011
3对应0110
4对应1110
76.34的十进制=1011 0011 . 0110 1110 1215BCD码
余三码
余3码的编码方式为：在8421BCD基础上，对每一组代码加3，故将这种代码叫作余3码，如果将余3码每个代码视为二进制数，使它等效的十进制数与所表示的代码相等，其代码中每一位1所代表的权值在各组代码中不是固定的，所以余3码表示不像8421BCD码那样直观，各位没有固定的权值，所以余3码是一种无权码
移存码移存码的编码方式是按移位寄存器中数码移位的规律进行编码，如果移存码为4位二进制数，根据移存过程，可以采用移存码代表0~9十个数码，所以该移存码也是属于二-十进制(BCD)码中的一种
十进制数\编码种类
有权码 无权码
8421码 2421码 5421码 5211码 1215码 余3码 移存码 0 0000 0000 0000 0000 0000 0011 0001 1 0001 0001 0001 0001 0010 0100 0010 2 0010 0010 0010 0011 0100 0101 0100 3 0011 0011 0011 0110 0110 0110 1001 4 0100 0100 0100 0111 1110 0111 0011 5 0101 1011 1000 1000 0001 1000 0111 6 0110 1100 1001 1001 0011 1001 1111
7 0111 1101 1010 1100 1011 1010 1110 8 1000 1110 1011 1110 1101 1011 1100 9 1001 1111 1100 1111 1111 1100 1000
格雷码
格雷码是无权码，又叫循环码，在编码形式上有多种不同方式，但都有一个共同的特点，就是任意两个相邻的代码之间仅有1位不同，其余各位均相同，并具有循环码的特点
十进制 二进制数 格雷码 0 0000 0000 1 0001 0001 2 0010 0011 3 0011 0010 4 0100 0110 5 0101 0111 6 0110 0101 7 0111 0100 8 1000 1100 9 1001 1101 10 1010 1111 11 1011 1110 12 1100 1010 13 1101 1011 14 1110 1001 15 1111 1000
特点
相邻项或对称项只有一位不同
将二进制转换为格雷码
(1)格雷码的最高位(最左边)与二进制数的最高位相同
(2)从左到右，逐一将二进制数相邻两位异或，作为格雷码的下一位
例如
二进制数1011转换成格雷码
从左到右
第一位二进制数写下来为1
第二位，看二进制数，第一位跟第二位异或，为1异或0为1
第三位，看二进制数，第二位跟第三位异或，为0异或1为1第四位，看二进制数，第三位和第四位异或，为1异或1为0
格雷码为1110
格雷码1110转换成二进制数从左到右
第一位写下来为1
第二位，看格雷码，将写下来的第一位与格雷码第二位异或，1异或1为0
第三位，看格雷码，将写下来第二位与格雷码第三位异或，0异或1为1
第四位，看格雷码，将写下来第三位与格雷码第四位异或，1异或0为1
所以二进制数为1011
奇偶校验码
在编码时，根据信息位中1的个数决定添加的校验位是1还是0，这样，使整个代码中1的个数按预先规定称为奇数或偶数
当信息位和校验位中1的个数为奇数时，称为奇校验码，而1的个数为偶数时，称为偶校验码
十进制数码 带奇校验的8421BCD码 带偶校验的8421BCD码
十进制数码 信息码 校验码 信息码 校验码 0 0000 1 0000 0 1 0001 0 0001 1 2 0010 0 0010 1 3 0011 1 0011 0 4 0100 0 0100 1 5 0101 1 0101 0 6 0110 1 0110 0 7 0111 0 0111 1 8 1000 0 1000 1 9 1001 1 1001 0
原码、反码和补码
关键术语
原码：数字的符号以0、1表示，数位部分与原值相同
反码：负数在原码基础上数位部分按位取反，正数与原码相同
补码：整数与原码相同，负数在反码基础上数位部分的末位加1构成
为了简化减法运算，一般转换为加法运算来进行，因此提出了有符号数的三种表示形式，分别为原码、反码和补码
原码
原码的编码规律为，正数的符号位用0表示，负数的符号位用1表示，数位部分则和真值完全一样
反码
又称为“对1的补数”，用反码表示时，数值的形式与它的符号位有关，左边第1位是符号位，符号位为0代表正数，符号位为1代表负数，对于负数，反码是将原码数位部分按位取反，而对于正数，反码和原码相同。
补码
具有许多特点，是数字系统中使用的一种编码，补码又称为“对2的补数”，在补码表示中，正数的表示与原码相同，而负数的补码符号位为1，数值位是将原码按位取反后末位加1
即正数的原码，反码和补码都相同
负数的反码为二进制每位取反
补码为取反后+1
例如
-10110的二进制原码，反码和补码
原码：110110
反码：101001
补码：101010
相关文章：
数制和码制
目录 几种常见的数制 数制 基数 位权 常见的四种数制 十进制数 二进制数 八进制数 十六进制数 不同进制数的相互转换 例如 例如 编码 二-十进制码 例如 格雷码 例如 原码、反码和补码 几种常见的数制 关键术语 数制：以一组固定的符号和统一的规则来表示数值…...
Git Bash中安装tree
文章目录 问题描述解决办法A备选办法BRef 问题描述 在Git Bash中使用tree报错： tree # bash: tree: command not found解决办法A 下载二进制文件： https://gnuwin32.sourceforge.net/packages/tree.htm -> 选binary。下载后解压.zip 把解压后的tre…...
java开源 VR全景商城 saas商城 b2b2c商城 o2o商城 积分商城 秒杀商城 拼团商城 分销商城 短视频商城 小程序商城搭建
1. 涉及平台 平台管理、商家端（PC端、手机端）、买家平台（H5/公众号、小程序、APP端（IOS/Android）、微服务平台（业务服务） 2. 核心架构 Spring Cloud、Spring Boot、Mybatis、Redis 3. 前端框架…...
C++练手题系列一
第 1 题 【 问答题 】 • 有多少种二叉树 输入n(1<n<13)，求n个结点的二叉树有多少种形态 时间限制：1000 内存限制：65536 输入 整数n 输出答案 样例输入 3 样例输出 5 第 2 题 【 问答题 】 • 城堡问题 1 2 3 4 5 6 7 ################…...
（下）async/await高级用法，你会多少种呢？
公众号：程序员白特，欢迎一起交流学习~ 前言 众所周知，在 ECMA17 中加入了两个关键字 async、await，简单来说它们是基于 Promise 之上的语法糖，可以让异步操作更加简洁明了。在掌握async、await的基础用法后࿰…...
阅读笔记 | REFORMER: THE EFFICIENT TRANSFORMER
阅读论文： Kitaev, Nikita, Łukasz Kaiser, and Anselm Levskaya. “Reformer: The efficient transformer.” arXiv preprint arXiv:2001.04451 (2020). 背景与动机 这篇论文发表较早，主要关注Transformer的效率问题。标准的Transformer模型在许多自然…...
光路科技：工业以太网交换机引领工业互联网新篇章
随着全球范围内工业4.0的浪潮不断涌动，工业互联网作为其核心驱动力，正引领着工业生产向智能化、网络化的崭新阶段迈进。在这一转型的浪潮中，光路科技凭借其卓越的工业互联设备与创新解决方案，正为工业互联网领域的发展注入新的活力…...
航拍无人机技术，航拍无人机方案详解，无人机摄影技术
航拍无人机是利用遥控技术和摄像设备，在空中进行拍摄和录像的无人机。这种无人机通常具有高清摄像设备、图像传输设备、GPS定位系统、智能控制系统等，可以轻松实现各种拍摄角度和高度，广泛应用于影视制作、旅游景区航拍、城市规划、环保监测等…...
【ArcPy】游标访问几何数据
访问质心坐标相关数据 结果展示 代码 import arcpy shppath r"C:\Users\admin\Desktop\excelfile\a2.shp" with arcpy.da.SearchCursor(shppath, ["SHAPE","SHAPEXY","SHAPETRUECENTROID","SHAPEX","SHAPEY",&q…...
Java云计算k8s
云计算k8s k8s简介容器技术的发展使用kubeadm安装k8skubectlKubernetes 架构k8s节点节点与控制面之间的通信控制器k8s kubectl命令详解k8s容器Kubernetes 对象Kubernetes 对象管理Kubernetes 对象管理 指令式命令Kubernetes 对象管理 指令式对象配置k8s对象管理 声明式对象配置…...
蜂窝物联：物联网大数据云平台功能模块简介
蜂窝云平台可远程获取现场环境（如温室大棚、稻田）的空气温湿度、土壤水分温度、二氧化碳浓度、光照强度及视频图像，通过数据模型分析，可以自动控制湿帘、风机、喷淋滴灌、内外遮阳、顶窗侧窗、加温补光、增氧机等设备；…...
Docker镜像导出/导入
Docker镜像导出/导入 一、前言 在实际操作中，为了便于docker镜像环境和服务配置的迁移，我们有时需要将已在测试环境主机上完成一系列配置的docker镜像或运行中的容器镜像导出，并传输到生产或其他目标环境主机上运行。为此，本文主…...
SwiftUI 如何在运行时从底层动态获取任何 NSObject 对象实例
概览 众所周知，SwiftUI 的推出极大地方便了我们这些秃头码农们搭建 App 界面。不过，有时我们仍然需要和底层的 UIKit 对象打交道。比如：用 SwiftUI 未暴露出对象的接口改变视图的行为或外观。 从上图可以看到，我们 SwiftUI 代码并没有设置视图的背景色，那么它是怎么变成绿…...
LeetCode 2161.根据给定数字划分数组
给你一个下标从 0 开始的整数数组 nums 和一个整数 pivot 。请你将 nums 重新排列，使得以下条件均成立： 所有小于 pivot 的元素都出现在所有大于 pivot 的元素 之前 。 所有等于 pivot 的元素都出现在小于和大于 pivot 的元素 中间 。 小于 pivot 的元素…...
ip获取+归属地实现
1.背景 现在的社交平台一般都需要展示用户的归属地，这个功能有下面二个主要功能点，接下来我们来介绍下具体实现。 IP 获取 IP 转归属地 2.ip获取 2.1 Http请求 对于controller的请求，我们只需要写个拦截器，将用户的ip设置进上下文即可，非常方便。 @Override public bo…...
Python的错误和异常
文章目录 python的语法错误异常异常处理用户自定义异常定义清理行为预定义的清理行为 python的语法错误 语法错误（Syntax Error）是指代码不符合Python语言的语法规则。当解释器在执行代码之前对其进行解析时，如果发现代码中有语法错误&#…...
C语言-------指针进阶（2）
1.指针数组 指针数组表较简单，类比整型数组，字符数组，整型数组里面的元素都是整型变量，字符数组里面 的元素是字符类型，那么指针数组就是数组里面的每个元素都是指针类型，例如int*arr[5]就是一个 指针数…...
Spring El表达式官方文档学习
文章目录 推荐一、概述1、什么是SpEL2、SpEL能做什么 二、SpEL表达式使用1、文字表达式2、属性, 数组, List, Map,和 索引（1）属性操作（2）数组和List（3）Map 3、内嵌List4、内嵌Map5、构建数组6、调用类的方法…...
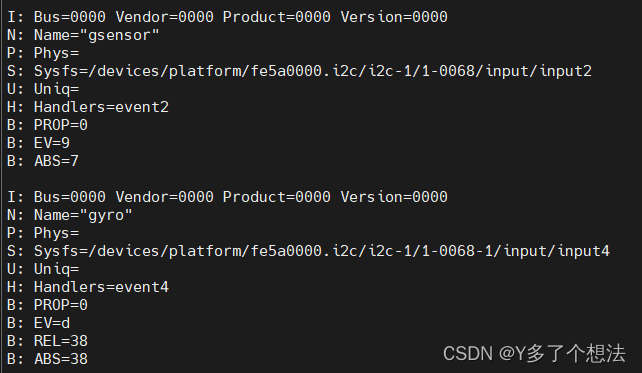
RK3568 android11 调试陀螺仪模块 MPU6500
一，MPU6500功能介绍 1.简介 MPU6500是一款由TDK生产的运动/惯性传感器，属于惯性测量设备（IMU）的一种。MPU6500集成了3轴加速度计、3轴陀螺仪和一个板载数字运动处理器（DMP），能够提供6轴的运动…...
【HTML】HTML基础6.1（表格以及常见属性）
目录 表格介绍 表格标签 表格标签的常见属性 案例 知识点总结 表格介绍 在浏览器中，我们经常见到形如 这样的表格形式，一般来说，表格是为了让数据看起来更加清晰，增强数据的可读性 有的程序员也会用表格进行排版 表格标签 &…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下： struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...
土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测；从基础到高级，涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术，可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势，还能有效评价重大生态工程…...
ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”（简单设计）是软件开发中的一个重要理念，倡导以最简单的方式实现软件功能，以确保代码清晰易懂、易维护，并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计，遵循“让事情保…...
算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer （1）资源 论文&a…...
MySQL 索引底层结构揭秘：B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识：什么是 B-Tree 和 BTree？ B-Tree（平衡多路查找树） BTree（B-Tree 的变种） 二、结构对比：一张图看懂 三、为什么 MySQL InnoDB 选择 BTree？ 1. 范围查询更快 2…...
破解路内监管盲区：免布线低位视频桩重塑停车管理新标准
城市路内停车管理常因行道树遮挡、高位设备盲区等问题，导致车牌识别率低、逃费率高，传统模式在复杂路段束手无策。免布线低位视频桩凭借超低视角部署与智能算法，正成为破局关键。该设备安装于车位侧方0.5-0.7米高度，直接规避树枝遮…...
c# 局部函数 定义、功能与示例
C# 局部函数：定义、功能与示例 1. 定义与功能 局部函数（Local Function）是嵌套在另一个方法内部的私有方法，仅在包含它的方法内可见。 • 作用：封装仅用于当前方法的逻辑，避免污染类作用域，提升…...
五子棋测试用例
一.项目背景 1.1 项目简介 传统棋类文化的推广 五子棋是一种古老的棋类游戏，有着深厚的文化底蕴。通过将五子棋制作成网页游戏，可以让更多的人了解和接触到这一传统棋类文化。无论是国内还是国外的玩家，都可以通过网页五子棋感受到东方棋类…...
Vue 3 + WebSocket 实战：公司通知实时推送功能详解
📢 Vue 3 WebSocket 实战：公司通知实时推送功能详解 📌 收藏 点赞 关注，项目中要用到推送功能时就不怕找不到了！ 实时通知是企业系统中常见的功能，比如：管理员发布通知后，所有用户…...
goreplay
1.github地址 https://github.com/buger/goreplay 2.简单介绍 GoReplay 是一个开源的网络监控工具，可以记录用户的实时流量并将其用于镜像、负载测试、监控和详细分析。 3.出现背景 随着应用程序的增长，测试它所需的工作量也会呈指数级增长。GoRepl…...