无人机飞行控制系统技术,四旋翼无人机控制系统建模技术详解
物理建模是四旋翼无人机控制系统建模的基础,主要涉及到无人机的物理特性和运动学特性。物理建模的目的是将无人机的运动与输入信号(如控制电压)之间的关系进行数学描述。
四旋翼无人直升机是具有四个输入力和六个坐标输出的欠驱动动力学旋翼式直升机,从而可知该系统是能够准静态飞行(盘旋飞行和近距离盘旋飞行)的自主飞行器。与传统的旋翼式无人机相比,四旋翼无人机只能通过改变旋翼的 转速来实现各种运动。与传统的直升机那种具有可变倾斜角不同的是,四旋翼无人直升机具有四个倾斜角固定的旋翼,因此结构和动力学特性得到了简化。

四旋翼无人机动态数学模型
任何系统的运动方程,都是针对某一特定的参考坐标系建立的。无人机在本质上属于多体动力学系统。无人机机身的运动可以看成六自由度的刚体运动,包含绕三个轴的转动和重心沿三个轴向的线运动。想要描述无人机的转动,须选用机体坐标系想要描述无人机的位置,须选用地面坐标系。
地面坐标系OXYZ
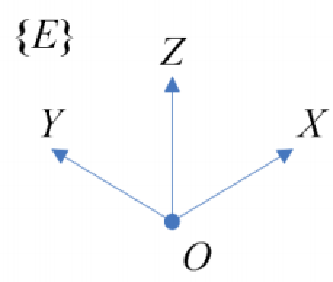
地面坐标系就是一种固定在地球表面的坐标系。首先在地面上选定一个原点 O,使得 X 轴指向地球表面的任意一个方向。Z 轴沿着铅直方向指向天,Y 轴在水平面内与 X 轴垂直,指向通过右手定则来确定。在忽略地球的自转运动和地球质心的 曲线运动时,该地面坐标系可看成是一个惯性坐标系。飞行器的位姿态、速度、角速度等都是相对于这一坐标系来衡量的。
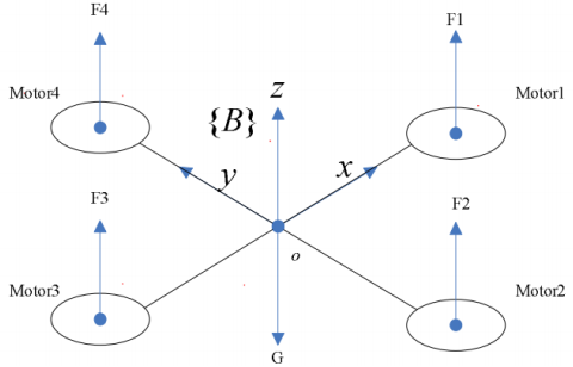
机体坐标系oxyz
坐标系固定在航飞行器上 并遵循右手法则的三维正交直角坐标系称为机体坐标系。原点 o 位于飞行器的质心处, x 轴在飞机的对称平面内,并且平行于飞行器的设计轴线,指向机头前 方。y 轴垂直于机身对称平面,并指向机身右方。z 轴的在飞行器对称平面内, 与 xoy 平面垂直,并指向飞行器的上方。
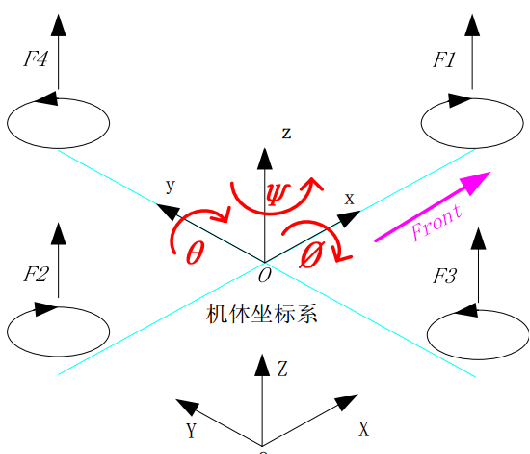
欧拉角
机体坐标系与地面坐标系的关系可以通过三个欧拉角进行表示,分别是俯仰角θ、滚转角Φ和偏航角ψ。
坐标转换矩阵
体坐标系和地面坐标系之间的转换满足下面关系式:
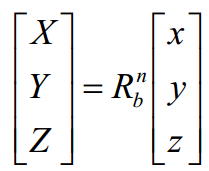
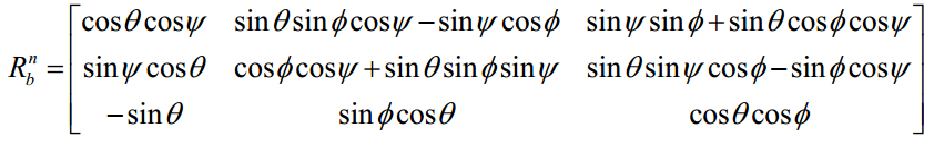
动力学模型的建立
根据牛顿第二定律,有:
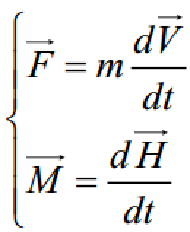

动力学模型的建立

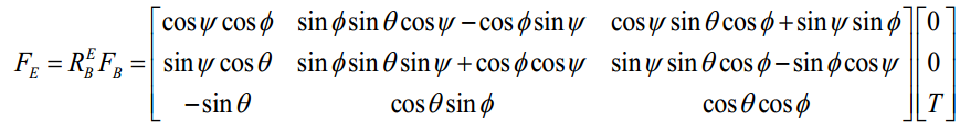
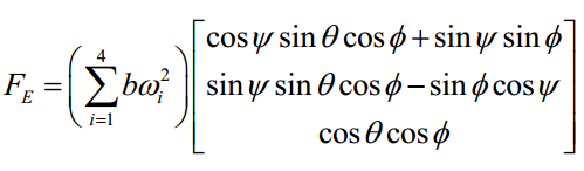
由牛顿第二定律以及飞行器的动力方程,飞行器载体在参考坐标系下的位移方程为:

由此可以得到位置坐标的线性位移方程:
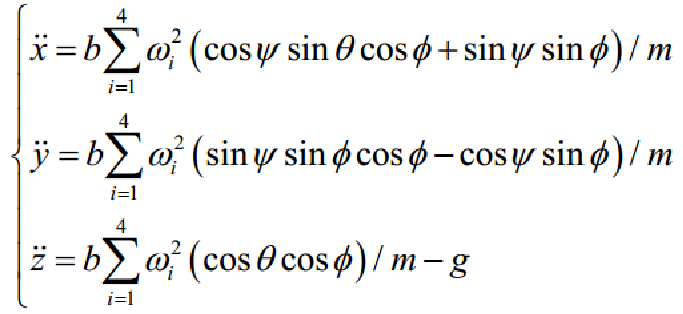
无人机应以动态坐标为基础进行动力学研究。由刚体的欧拉方程,绝对导数在动态坐标下可以表示为:
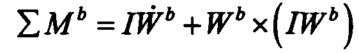
其中(p,q,r分别为机体坐标系上的横滚,俯仰,偏航角速度):
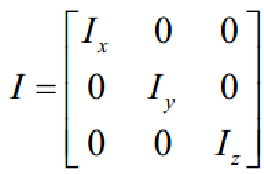
整理得到:
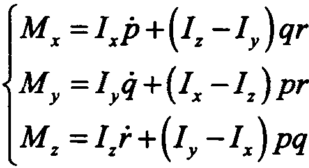
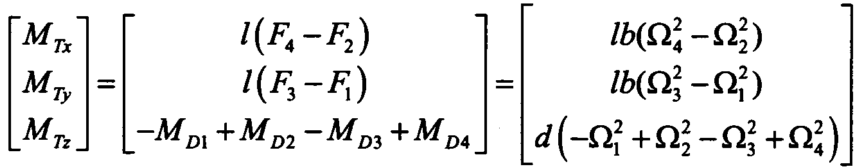
![]()
由欧拉角方程可以飞行器的角运动方程:
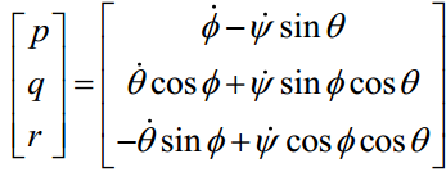
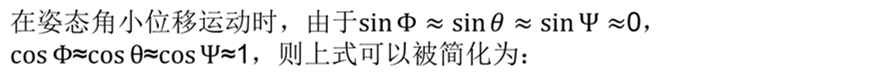

定义:
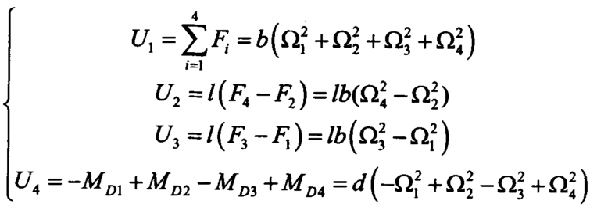
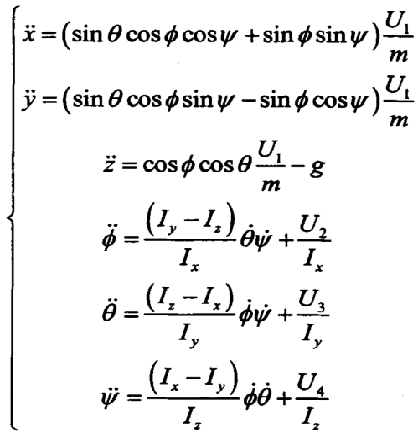
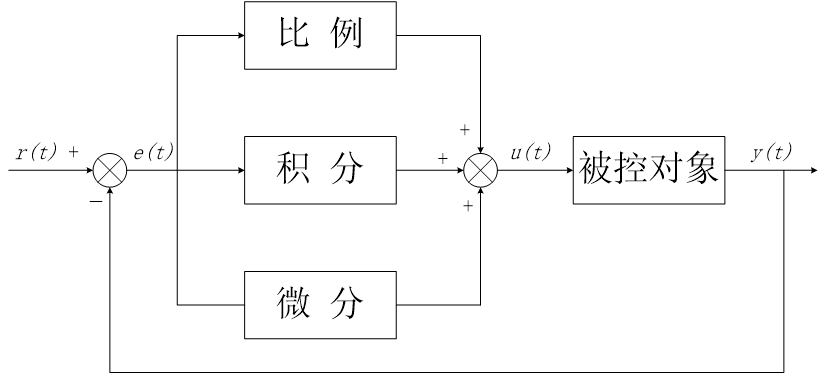
PID控制
PID控制是一种经典的闭环反馈控制方法,它广泛应用于多种工业控制系统。经典PID控制由比例环节、积分环节和微分环节三部分组成。控制系统以测量值y(t)和设定值r(t)之间的误差值e(t)作为输入量,通过对误差e(t)进行比例、积分和微分运算使控制系统输出量u(t)的误差最小化。
![]()
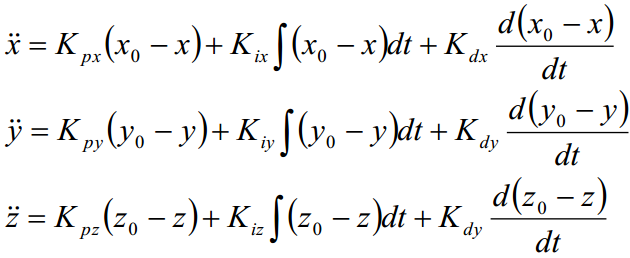
由动力学方程可得俯仰角θ、滚转角Φ的理想值:
![]()
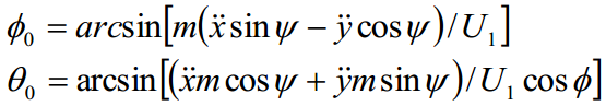
由姿态角PID后得到:
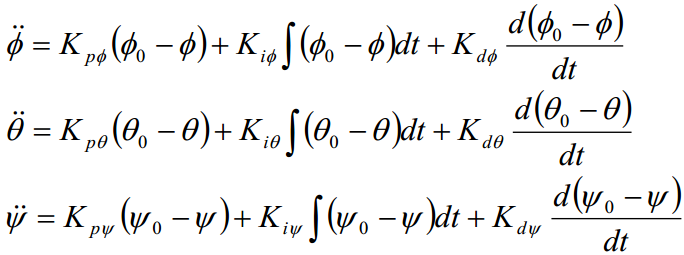


在四旋翼无人机中,无人机的运动主要受到四个电机的旋转速度的影响。每个电机通过旋翼产生升力,进而影响无人机的位置和姿态。因此,物理建模需要建立无人机的位置、速度、加速度、角速度、姿态等运动参数与电机旋转速度之间的关系。
系统集成与验证
系统集成与验证是对四旋翼无人机控制系统建模效果的检验和确认,也是在实际应用中对无人机性能进行评估的重要环节。
在系统集成阶段,需要将物理模型、数学模型和控制算法进行整合,构建完整的四旋翼无人机控制系统。在这个过程中,需要考虑到无人机的硬件限制和实际应用环境,确保系统能够稳定运行。
验证阶段则是对控制系统性能的评估和测试。通过在仿真环境或实际飞行中对无人机的性能进行测试,可以评估控制算法的有效性和稳定性。同时,也可以通过调整控制参数来优化无人机的性能表现。
相关文章:

无人机飞行控制系统技术,四旋翼无人机控制系统建模技术详解
物理建模是四旋翼无人机控制系统建模的基础,主要涉及到无人机的物理特性和运动学特性。物理建模的目的是将无人机的运动与输入信号(如控制电压)之间的关系进行数学描述。 四旋翼无人直升机是具有四个输入力和六个坐标输出的欠驱动动力学旋翼…...

程序员的金三银四求职宝典:如何在关键时期脱颖而出?
个人主页:17_Kevin-CSDN博客 随着春天的脚步渐近,程序员们的求职热潮也随之而来。在这个被称为“金三银四”的招聘季,如何从众多求职者中脱颖而出,成为了许多程序员关注的焦点。本文将为你提供一份全面的求职宝典,助你…...

分享经典、现代和前沿软件工程课程
随着信息技术的发展,软件已经深入到人类社会生产和生活的各个方面。软件工程是将工程化的方法运用到软件的开发、运行和维护之中,以达到提高软件质量,降低开发成本的目的。软件工程已经成为当今最活跃、最热门的学科之一。 本次软件工程MOOC课…...
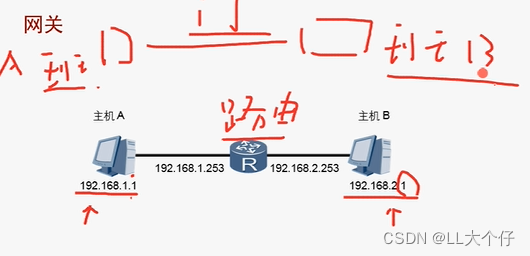
网络工程师笔记3
IP地址类型 A类 255.0.0.0B类 255.255.0.0C类 255.255.255.0D类 E类 子网掩码:从左到右连续的确定网络位 2-4-8-16-32-64-128-256 128 : 1000 0000 64 : 0100 0000 32 : 0010 0000 16 : 0001 0000 8 &am…...

【菜鸟入门!】Matlab零基础快速入门教程
数学建模竞赛中,编程软件是必不可缺少的,比如大家都熟知的MATLAB多数同学们都会经常用到,今天给大家介绍一些MATLAB的基本元素,希望帮助大家更好的掌握编写基本的函数! 变量和数组 MATLAB 程序的基本数据单元是数组。一…...
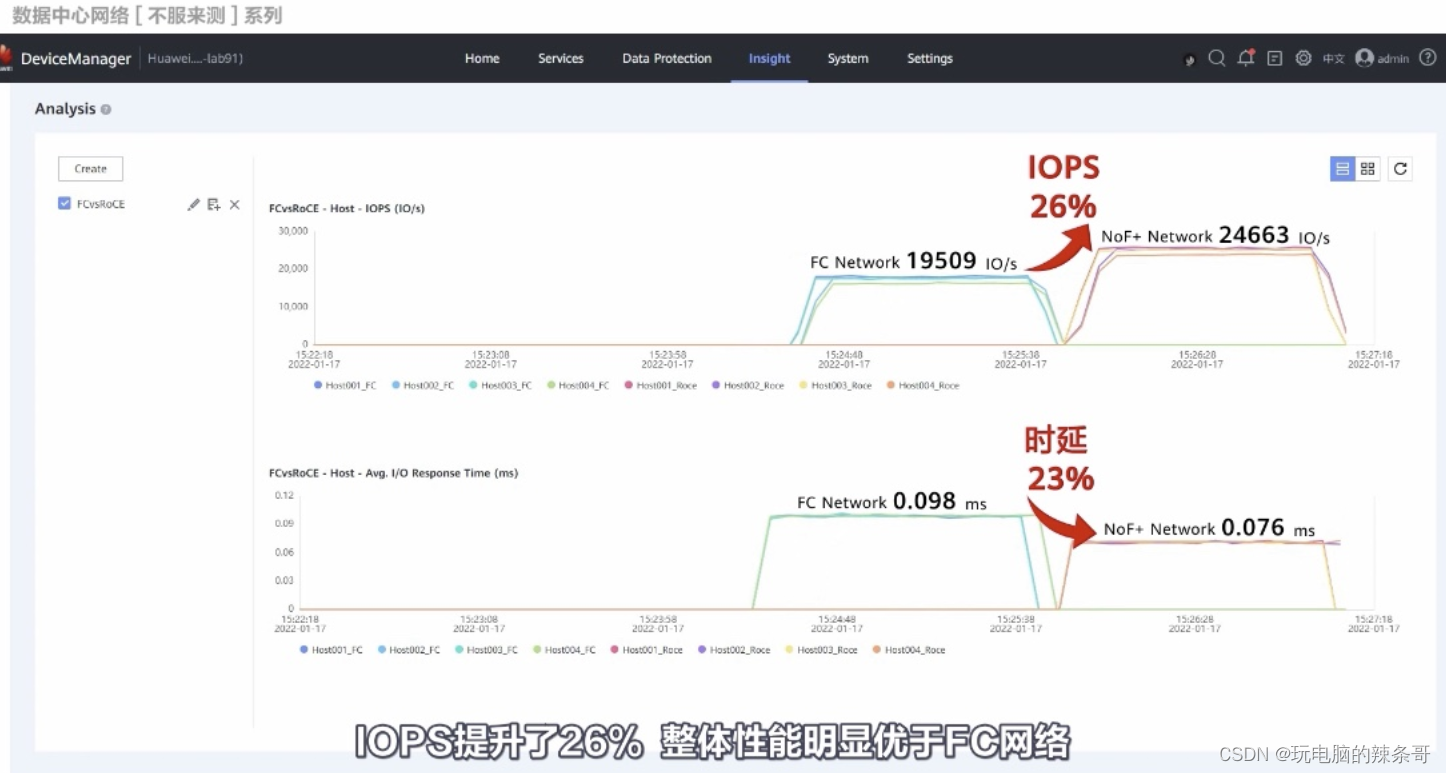
数据中心GPU集群高性能组网技术分析
数据中心GPU集群组网技术是指将多个GPU设备连接在一起,形成一个高性能计算的集群系统。通过集群组网技术,可以实现多个GPU设备之间的协同计算,提供更大规模的计算能力,适用于需要大规模并行计算的应用场景。 常用的组网技术&…...

go垃圾回收
1 go 垃圾回收变更 Go 语言的垃圾回收器(GC)自其诞生以来一直在不断演进和优化,以提高性能、减少暂停时间和对程序执行的影响。以下是一些关键的改进和变更点: 并发标记周期: Go 语言从一开始就采用了并发标记…...

如何做代币分析:以 LEO 币为例
作者: lesleyfootprint.network 编译:cicifootprint.network 数据源:LEO 代币仪表板 (仅包括以太坊数据) 在加密货币和数字资产领域,代币分析起着至关重要的作用。代币分析指的是深入研究与代币相关的数…...

数制和码制
目录 几种常见的数制 数制 基数 位权 常见的四种数制 十进制数 二进制数 八进制数 十六进制数 不同进制数的相互转换 例如 例如 编码 二-十进制码 例如 格雷码 例如 原码、反码和补码 几种常见的数制 关键术语 数制:以一组固定的符号和统一的规则来表示数值…...

Git Bash中安装tree
文章目录 问题描述解决办法A备选办法BRef 问题描述 在Git Bash中使用tree报错: tree # bash: tree: command not found解决办法A 下载二进制文件: https://gnuwin32.sourceforge.net/packages/tree.htm -> 选binary。下载后解压.zip 把解压后的tre…...
java开源 VR全景商城 saas商城 b2b2c商城 o2o商城 积分商城 秒杀商城 拼团商城 分销商城 短视频商城 小程序商城搭建
1. 涉及平台 平台管理、商家端(PC端、手机端)、买家平台(H5/公众号、小程序、APP端(IOS/Android)、微服务平台(业务服务) 2. 核心架构 Spring Cloud、Spring Boot、Mybatis、Redis 3. 前端框架…...

C++练手题系列一
第 1 题 【 问答题 】 • 有多少种二叉树 输入n(1<n<13),求n个结点的二叉树有多少种形态 时间限制:1000 内存限制:65536 输入 整数n 输出答案 样例输入 3 样例输出 5 第 2 题 【 问答题 】 • 城堡问题 1 2 3 4 5 6 7 ################…...
async/await高级用法,你会多少种呢?)
(下)async/await高级用法,你会多少种呢?
公众号:程序员白特,欢迎一起交流学习~ 前言 众所周知,在 ECMA17 中加入了两个关键字 async、await,简单来说它们是基于 Promise 之上的语法糖,可以让异步操作更加简洁明了。在掌握async、await的基础用法后࿰…...

阅读笔记 | REFORMER: THE EFFICIENT TRANSFORMER
阅读论文: Kitaev, Nikita, Łukasz Kaiser, and Anselm Levskaya. “Reformer: The efficient transformer.” arXiv preprint arXiv:2001.04451 (2020). 背景与动机 这篇论文发表较早,主要关注Transformer的效率问题。标准的Transformer模型在许多自然…...

光路科技:工业以太网交换机引领工业互联网新篇章
随着全球范围内工业4.0的浪潮不断涌动,工业互联网作为其核心驱动力,正引领着工业生产向智能化、网络化的崭新阶段迈进。在这一转型的浪潮中,光路科技凭借其卓越的工业互联设备与创新解决方案,正为工业互联网领域的发展注入新的活力…...

航拍无人机技术,航拍无人机方案详解,无人机摄影技术
航拍无人机是利用遥控技术和摄像设备,在空中进行拍摄和录像的无人机。这种无人机通常具有高清摄像设备、图像传输设备、GPS定位系统、智能控制系统等,可以轻松实现各种拍摄角度和高度,广泛应用于影视制作、旅游景区航拍、城市规划、环保监测等…...
【ArcPy】游标访问几何数据
访问质心坐标相关数据 结果展示 代码 import arcpy shppath r"C:\Users\admin\Desktop\excelfile\a2.shp" with arcpy.da.SearchCursor(shppath, ["SHAPE","SHAPEXY","SHAPETRUECENTROID","SHAPEX","SHAPEY",&q…...

Java云计算k8s
云计算k8s k8s简介容器技术的发展使用kubeadm安装k8skubectlKubernetes 架构k8s节点节点与控制面之间的通信控制器k8s kubectl命令详解k8s容器Kubernetes 对象Kubernetes 对象管理Kubernetes 对象管理 指令式命令Kubernetes 对象管理 指令式对象配置k8s对象管理 声明式对象配置…...
蜂窝物联:物联网大数据云平台功能模块简介
蜂窝云平台可远程获取现场环境(如温室大棚、稻田)的空气温湿度、土壤水分温度、二氧化碳浓度、光照强度及视频图像,通过数据模型分析,可以自动控制湿帘、风机、喷淋滴灌、内外遮阳、顶窗侧窗、加温补光、增氧机等设备;…...

Docker镜像导出/导入
Docker镜像导出/导入 一、前言 在实际操作中,为了便于docker镜像环境和服务配置的迁移,我们有时需要将已在测试环境主机上完成一系列配置的docker镜像或运行中的容器镜像导出,并传输到生产或其他目标环境主机上运行。为此,本文主…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...
