[LeetBook]【学习日记】寻找和为指定数字的连续数字
题目
文件组合
待传输文件被切分成多个部分,按照原排列顺序,每部分文件编号均为一个 正整数(至少含有两个文件)。传输要求为:连续文件编号总和为接收方指定数字 target 的所有文件。请返回所有符合该要求的文件传输组合列表。
注意,返回时需遵循以下规则:
每种组合按照文件编号 升序 排列; 不同组合按照第一个文件编号 升序 排列。
示例 1:
输入:target = 12 输出:[[3, 4, 5]] 解释:在上述示例中,存在一个连续正整数序列的和为 12,为 [3, 4, 5]。
示例 2:输入:target = 18 输出:[[3,4,5,6],[5,6,7]] 解释:在上述示例中,存在两个连续正整数序列的和分别为18,分别为 [3, 4, 5, 6] 和 [5, 6, 7]。
提示:
1 <= target <= 10^5
解法1:分类
- 这种做法是笔者最朴素的想法:如果遍历小于 target 的每一个数,逐个相加尝试该数是否能组成一个符合条件的文件序列,那时间复杂度太高了(其实这种就是滑动窗口的思想,复杂度只有O(N))。于是我想能否在遍历到这个数的同时,直接根据这个数与 target 之间的某种关系判断其能否形成合适的序列,于是在观察到文件序列其实是等差数列后,我决定依据等差数列的特点对其进行分类
- 使用 i 进行遍历。文件序列如果有奇数个元素,则可以找到等差中项,target 能整除 i 且 n = target / i 必须为奇数
- 文件序列如果有偶数个元素,则target 能整除 i + i+1 且 n 和 target 的奇偶必须相同(!((n+target)%2))(因为n 表示有n对i + i+1,而i + i+1必为奇数,所以当n为偶数的时候,n对i + i+1的和为偶数;n为奇数的时候,n对i + i+1的和为奇数。所以 n 和 target 的奇偶必须相同)
- 由于题目要求不同组合按照第一个文件编号 升序 排列,而当我遍历 i 时,无法确定由 i 作为靠中间的元素的这个序列的头部是多少,所以我使用了 map 存储,利用了 map 会自动排序 key 的特点(结构:map<第一个文件编号,文件编号序列的 vector>)
class Solution {
public:vector<vector<int>> fileCombination(int target) {vector<vector<int>> all;map<int, vector<int>> forOrder;for(int i=1; i<=(target+1)/2; ++i){if(!(target%i)){//target 能整除 i,则可能的组合有奇数个元素int n = target / i;if(n%2 && i>n/2){//n 为组合中元素的个数,必须为奇数vector<int> group;for(int j=i-n/2; j<=i+n/2; ++j){group.push_back(j);}forOrder[i-n/2] = group;}}if(!(target%(i + i+1))){//target 能整除 i + i+1,可能的组合必为偶数个元素int n = target/(i + i+1);if(!((n+target)%2) && i-(n-1)>0){//n 和 target 的奇偶必须相同vector<int> group;for(int j=i-(n-1); j<=(i+1)+(n-1); ++j){group.push_back(j);}forOrder[i-(n-1)] = group;}}}// 将 forOrder 中的元素按顺序存入 all 中for (const auto& pair : forOrder) {all.push_back(pair.second);}return all;}
};
解法2:滑动窗口(双指针)
- 这种想法也很简单,从 i=1 开始,计算其后连续的序列的和,如果和小于 target,那么就在和的基础上往后再加一个数字;如果和大于 target 了,则表明此时的 i 作为开始元素找不到合适的序列,此时 i 往后移动,并记得让和减去上一个 i
- 这种想法虽然是遍历求和,并比较和与目标值,但是时间复杂度并不高,这是因为每次遍历和的计算都是在上一轮和的计算结果上进行的
- 由于是从 i=1 开始遍历,逐渐求和比较,故不存在有的序列会遍历不到的问题
//滑动窗口vector<vector<int>> fileCombination(int target) {vector<vector<int>> all;int i=1, j=2, sum=i+j;while(i<j){if(sum == target){vector<int> group;for(int k=i; k<=j; ++k){group.push_back(k);}all.push_back(group);}if(sum < target){++j;sum += j;// cout<<"j:"<<j<<"sum"<<sum<<endl;} else{sum -= i;++i;}}return all;}
解法3:等比数列求和公式求解
- 知道序列和 target,知道首项 i,那么可以利用等差数列求和公式 + 二次方程求根公式求出末项 j,遍历 i 找到所有符合的末项 j 即可。由于是使用公式计算,时间复杂度并不高
- 当 j 为整数时,符合条件,此处的判断方法为:if(j == (int)j)
- c++ 中,有int i,当 ii 结果超过int时,需要写成(long)ii,表达式 ii 的结果会首先根据表达式中操作数的类型来决定。如果 i 是整型(int),那么表达式 ii 也会被视为整型运算。
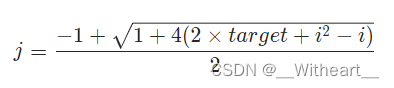
//等差求和公式做法vector<vector<int>> fileCombination(int target) {vector<vector<int>> all;for(int i=1; i<(target+1)/2; ++i){double j = (-1+sqrt(1+4*(2*target+(long)i*i-i)))/2.0;if(j == (int)j){vector<int> group;for(int k=i; k<=(int)j; ++k){group.push_back(k);}all.push_back(group);}}return all;}
相关文章:
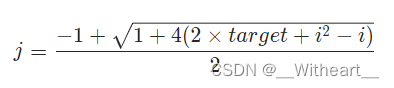
[LeetBook]【学习日记】寻找和为指定数字的连续数字
题目 文件组合 待传输文件被切分成多个部分,按照原排列顺序,每部分文件编号均为一个 正整数(至少含有两个文件)。传输要求为:连续文件编号总和为接收方指定数字 target 的所有文件。请返回所有符合该要求的文件传输组…...

阿里云中小企业扶持权益
为企业提供云资源和技术服务,助力企业开启智能时代创业新范式。阿里云推出中小企业扶持权益 上云必备,助力企业长期低成本用云 一、ECS-经济型e实例、ECS u1实例活动规则 活动时间 2023年10月31日0点0分0秒至2026年3月31日23点59分59秒 活动对象 同时满…...

2核4g服务器能支持多少人访问?并发数性能测评
2核4g服务器能支持多少人访问?支持80人同时访问,阿腾云使用阿里云2核4G5M带宽服务器,可以支撑80个左右并发用户。阿腾云以Web网站应用为例,如果视频图片媒体文件存储到对象存储OSS上,网站接入CDN,还可以支持…...

Anthropic官宣Claude3:建立大模型 推理、数学、编码和视觉等方面 新基准
文章目录 1. product2. Main2.1 核心能力2.2 打榜表现 3. My thoughtsReference Claude 3 在推理、数学、编码、多语言理解和视觉方面,全面超越GPT-4在内的所有大模型,重新树立大模型基准。 1. product https://claude.ai/ 国内暂不能使用,…...
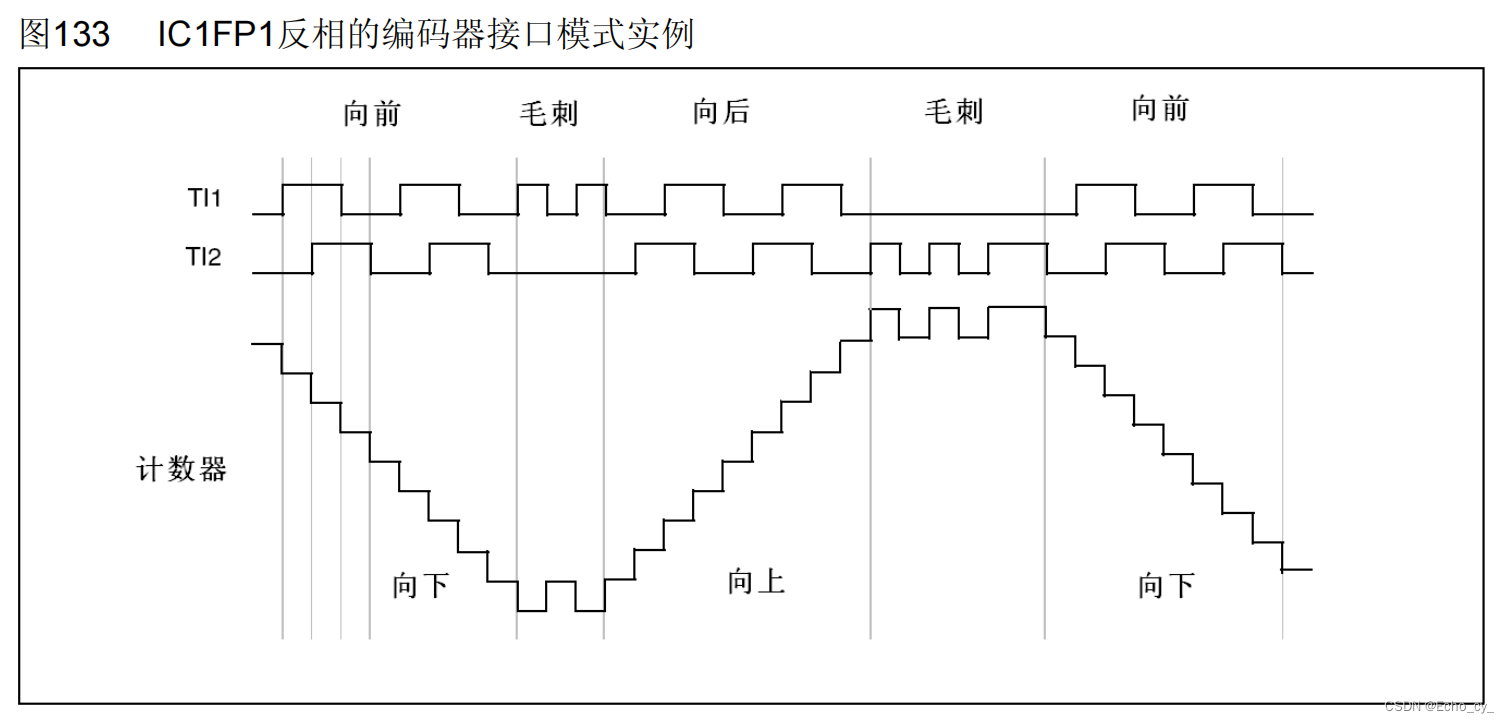
STM32 TIM编码器接口
单片机学习! 目录 文章目录 前言 一、编码器接口简介 1.1 编码器接口作用 1.2 编码器接口工作流程 1.3 编码器接口资源分布 1.4 编码器接口输入引脚 二、正交编码器 2.1 正交编码器功能 2.2 引脚作用 2.3 如何测量方向 2.4 正交信号优势 2.5 执行逻辑 三、编码器定时…...

Jupyter Notebook的安装和使用(windows环境)
一、jupyter notebook 安装 前提条件:安装python环境 安装python环境步骤: 1.下载官方python解释器 2.安装python 3.命令行窗口敲击命令pip install jupyter 4.安装jupyter之后,直接启动命令jupyter notebook,在默认浏览器中打开jupyte…...
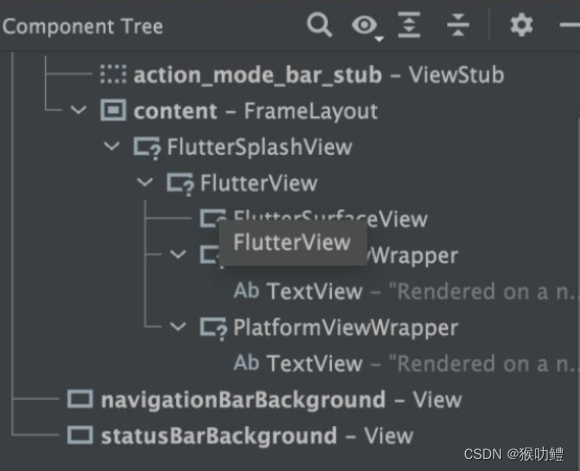
Platformview在iOS与Android上的实现方式对比
Android中早期版本Platformview的实现基于Virtual Display。VirtualDisplay方案的原理是,先将Native View绘制到虚显,然后Flutter通过从虚显输出中获取纹理并将其与自己内部的widget树进行合成,最后作为Flutter在 Android 上更大的纹理输出的…...
使用lnmp环境部署laravel框架需要注意的点
1,上传项目文件后,需要chmod -R 777 storage授予文件权限,不然会报错file_put_contents(/): failed to open stream: Permission denied。 如果后面还是报错没有权限的话,就执行ps -ef |grep php查询php运行用户。然后执行chown …...

AI-RAN联盟在MWC24上正式启动
AI-RAN联盟在MWC24上正式启动。它的logo是这个样的: 2月26日,AI-RAN联盟(AI-RAN Alliance)在2024年世界移动通信大会(MWC 2024)上成立。创始成员包括亚马逊云科技、Arm、DeepSig、爱立信、微软、诺基亚、美…...

Reactor详解
目录 1、快速上手 介绍 2、响应式编程 2.1. 阻塞是对资源的浪费 2.2. 异步可以解决问题吗? 2.3.1. 可编排性与可读性 2.3.2. 就像装配流水线 2.3.3. 操作符(Operators) 2.3.4. subscribe() 之前什么都不会发生 2.3.5. 背压 2.3.6. …...

实践航拍小目标检测,基于YOLOv5全系列【n/s/m/l/x】参数模型开发构建无人机航拍场景下的小目标检测识别分析系统
关于无人机相关的场景在我们之前的博文也有一些比较早期的实践,感兴趣的话可以自行移步阅读即可: 《deepLabV3Plus实现无人机航拍目标分割识别系统》 《基于目标检测的无人机航拍场景下小目标检测实践》 《助力环保河道水质监测,基于yolov…...

分布式数据库中全局自增序列的实现
自增序列广泛使用于数据库的开发和设计中,用于生产唯一主键、日志流水号等唯一ID的场景。传统数据库中使用Sequence和自增列的方式实现自增序列的功能,在分布式数据库中兼容Oracle和MySQL等传统数据库语法,也是基于Sequence和自增列的方式实现…...
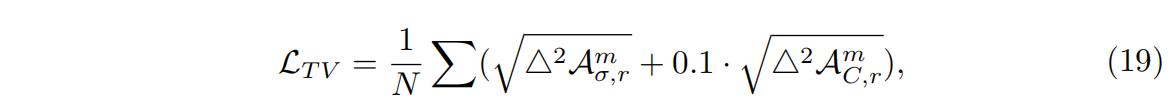
【论文阅读】TensoRF: Tensorial Radiance Fields 张量辐射场
发表于ECCV2022. 论文地址:https://arxiv.org/abs/2203.09517 源码地址:https://github.com/apchenstu/TensoRF 项目地址:https://apchenstu.github.io/TensoRF/ 摘要 本文提出了TensoRF,一种建模和重建辐射场的新方法。不同于Ne…...

深入了解 Android 中的 FrameLayout 布局
FrameLayout 是 Android 中常用的布局之一,它允许子视图堆叠在一起,可以在不同位置放置子视图。在这篇博客中,我们将详细介绍 FrameLayout 的属性及其作用。 <FrameLayout xmlns:android"http://schemas.android.com/apk/res/androi…...
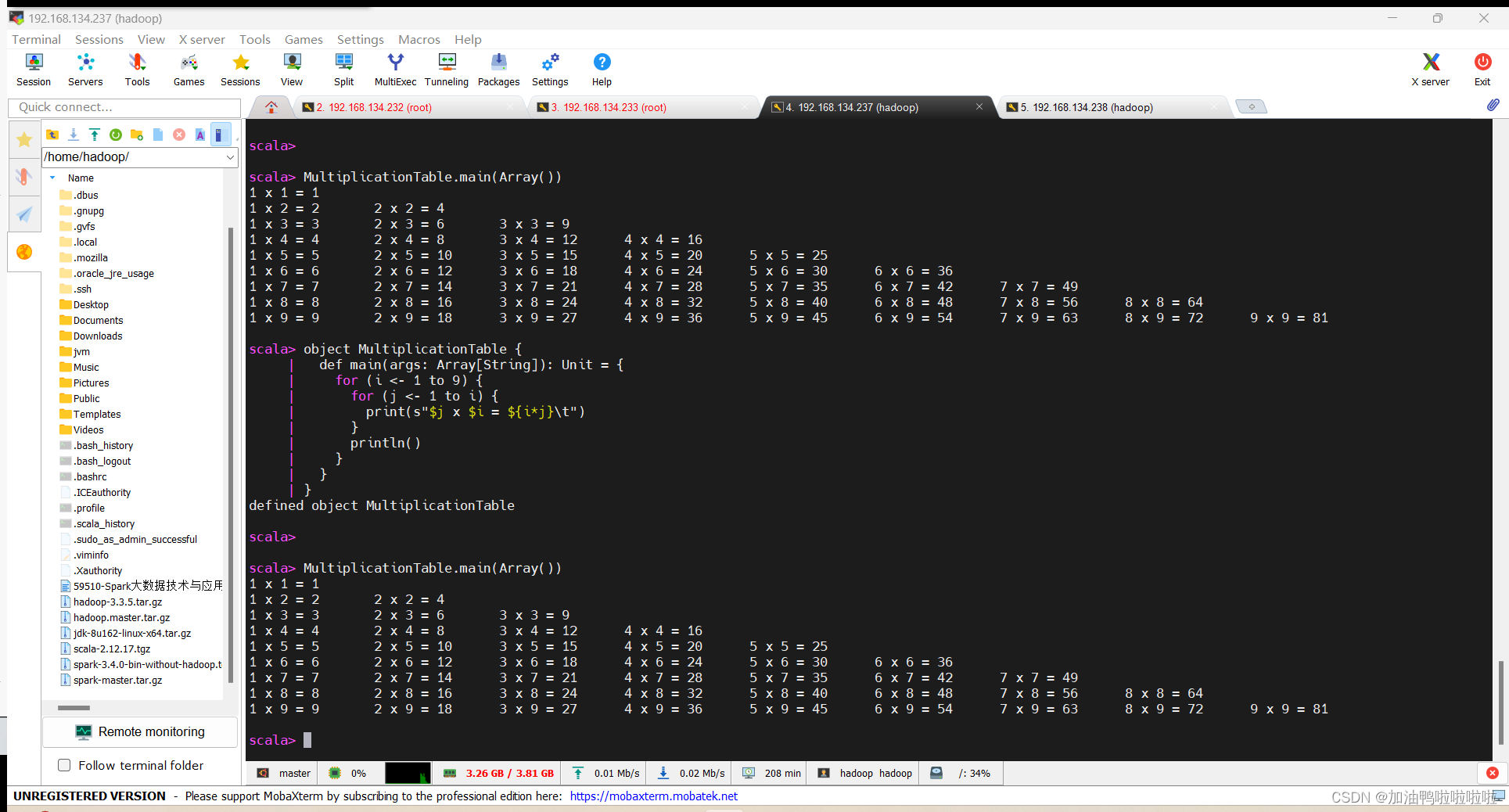
高级大数据技术 实验一 scala编程
高级大数据技术 实验一 scala编程 写的不是很好,大家多见谅! 1. 计算水仙花数 实验目标; (1) 掌握scala的数组,列表,映射的定义与使用 (2) 掌握scala的基本编程 实验说明 …...

使用Fabric创建的canvas画布背景图片,自适应画布宽高
之前的文章写过vue2使用fabric实现简单画图demo,完成批阅功能;但是功能不完善,对于很大的图片就只能显示一部分出来,不符合我们的需求。这就需要改进,对我们设置的背景图进行自适应。 有问题的canvas画布背景 修改后的…...
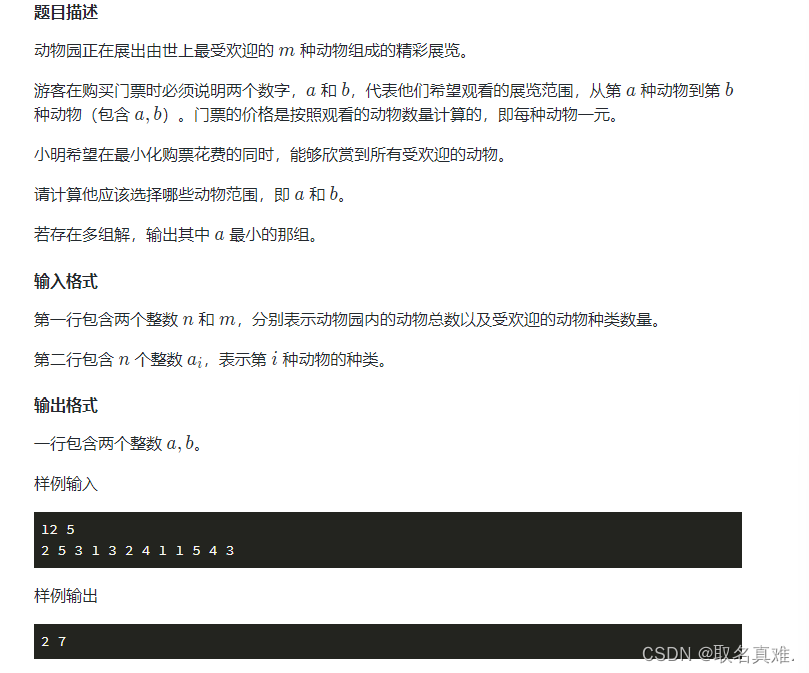
枚举与尺取法(蓝桥杯 c++ 模板 题目 代码 注解)
目录 组合型枚举(排列组合模板()): 排列型枚举(全排列)模板: 题目一(公平抽签 排列组合): 编辑 代码: 题目二(座次问题 全排…...

11、电源管理入门之Regulator驱动
目录 1. Regulator驱动是什么? 2. Regulator框架介绍 2.1 regulator consumer 2.2 regulator core 2.3 regulator driver 3. DTS配置文件及初始化 4. 运行时调用 5. Consumer API 5.1 Consumer Regulator Access (static & dynamic drivers) 5.2 Regulator Outp…...

24年证券从业考试注册报名流程详细图解,千万不要错过报名哦!
(一)时间安排 考生报名缴费时间:3月5日15时至3月8日15时 退费时间:3月7日15时至3月10日15时 准考证打印时间:3月20日15时至3月23日18时 (二)注册流程 1、进入中国证券业协会网站-从业人员管理-考…...
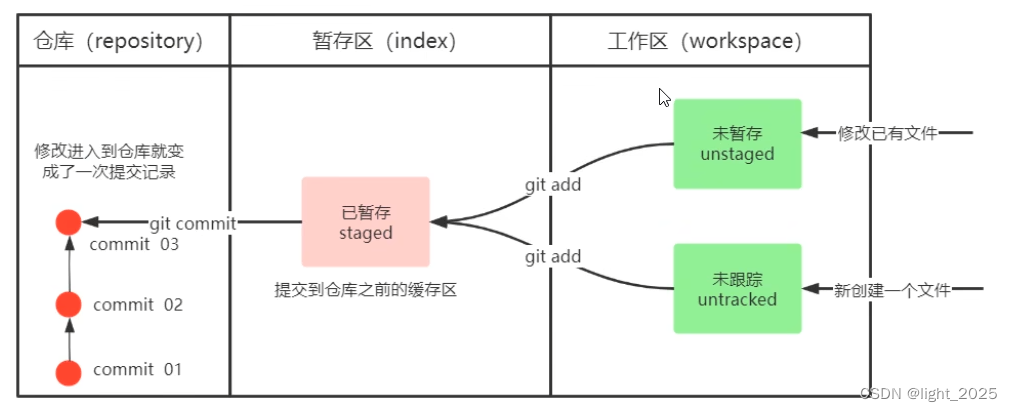
Git入门学习笔记
Git 是一个非常强大的分布式版本控制工具! 在下载好Git之后,鼠标右击就可以显示 Git Bash 和 Git GUI,Git Bash 就像是在电脑上安装了一个小型的 Linux 系统! 1. 打开 Git Bash 2. 设置用户信息(这是非常重要的&…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

Ubuntu Cursor升级成v1.0
0. 当前版本低 使用当前 Cursor v0.50时 GitHub Copilot Chat 打不开,快捷键也不好用,当看到 Cursor 升级后,还是蛮高兴的 1. 下载 Cursor 下载地址:https://www.cursor.com/cn/downloads 点击下载 Linux (x64) ,…...

十九、【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建
【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建 前言准备工作第一部分:回顾 Django 内置的 `User` 模型第二部分:设计并创建 `Role` 和 `UserProfile` 模型第三部分:创建 Serializers第四部分:创建 ViewSets第五部分:注册 API 路由第六部分:后端初步测…...
