优先级队列（Java ）

一、 优先级队列

1、概念

优先级队列（Priority
Queue）是一种特殊的队列，它根据元素的优先级进行排序。优先级队列的实现通常依赖于堆数据结构，可以是最大堆或最小堆。

二、优先级队列的模拟实现

1、堆的概念

如果有一个关键码的集合K = {k0，k1， k2，…，kn-1}，把它的所有元素按完全二叉树的顺序存储方式存储 在一个一维数组中，并满足：Ki <= K2i+1 且 Ki<= K2i+2 (Ki >= K2i+1 且 Ki >= K2i+2) i = 0，1，2…，则称为 小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。

堆的性质：
堆中某个节点的值总是不大于或不小于其父节点的值；
堆总是一棵完全二叉树。

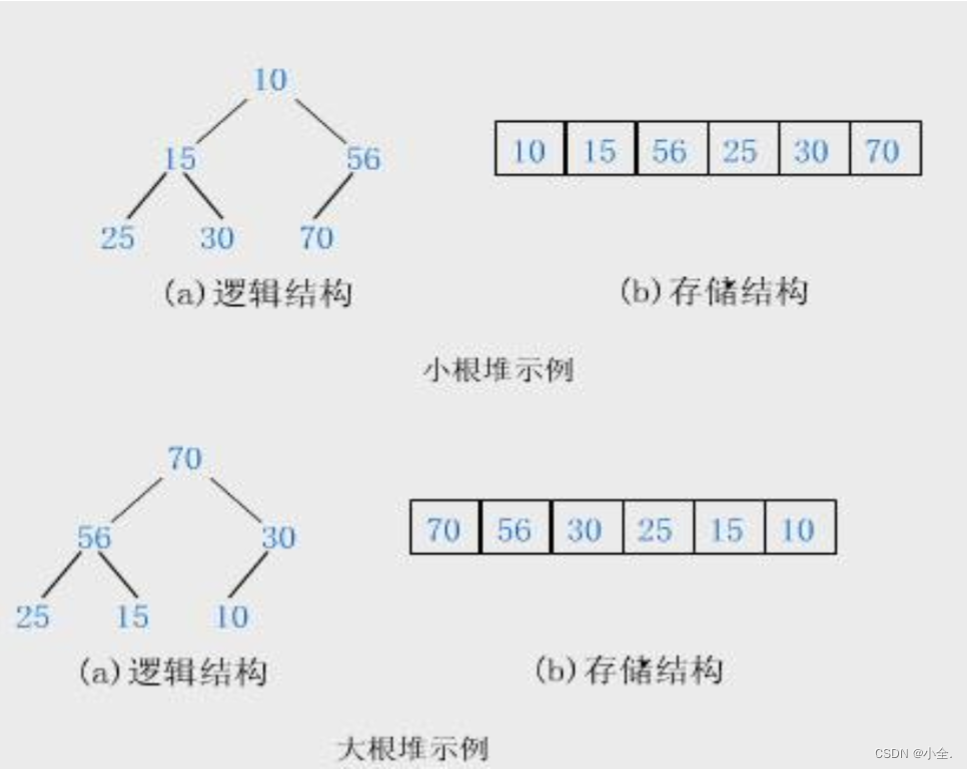
2、堆的存储方式

从堆的概念可知，堆是一棵完全二叉树，因此可以层序的规则采用顺序的方式来高效存储

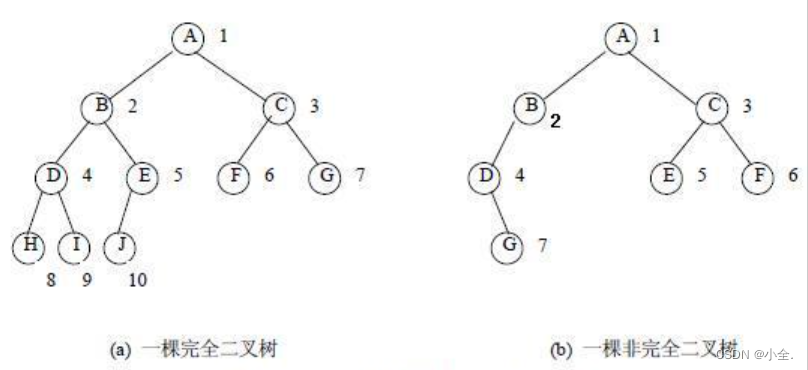
注意：对于非完全二叉树，则不适合使用顺序方式进行存储，因为为了能够还原二叉树，空间中必须要存储空节点，就会导致空间利用率比较低。

将元素存储到数组中后，可以根据二叉树章节的性质5对树进行还原。假设i为节点在数组中的下标，则有：
如果i为0，则i表示的节点为根节点，否则i节点的双亲节点为 (i - 1)/2
如果2 * i + 1 小于节点个数，则节点i的左孩子下标为2 * i + 1，否则没有左孩子
如果2 * i + 2 小于节点个数，则节点i的右孩子下标为2 * i + 2，否则没有右孩子

三、堆的创建

1、堆向下调整

我们来思考一个问题：对于集合{ 27,15,19,18,28,34,65,49,25,37 }中的数据，如果将其创建成堆呢？

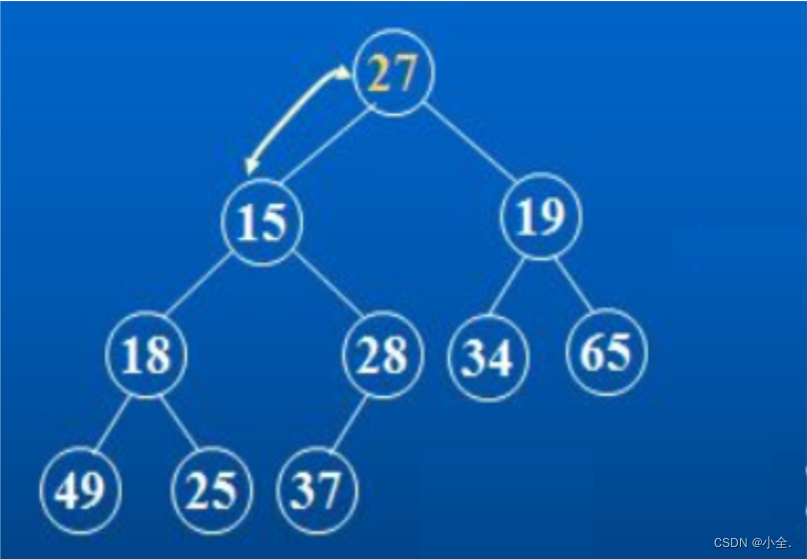
仔细观察上图后发现：根节点的左右子树已经完全满足堆的性质，因此只需将根节点向下调整好即可。

向下过程(以小堆为例)：

1. 让 parent 标记需要调整的节点， child 标记 parent 的左孩子 (注意：parent如果有孩子一定先是有左孩子)
2. 如果 parent 的左孩子存在，即 :child < size ， 进行以下操作，直到 parent 的左孩子不存在
   （1）parent右孩子是否存在，存在找到左右孩子中最小的孩子，让 child 进行标
   （2）将parent 与较小的孩子 child 比较，如果： parent 小于较小的孩子 child ，调整结束 否则：交换 parent 与较小的孩子 child ，交换完成之后， parent
   中大的元素向下移动，可能导致子树不满足对的性质，因此需要继续向下调整，即parent = child ； child =
   parent*2+1; 然后继续 2 。

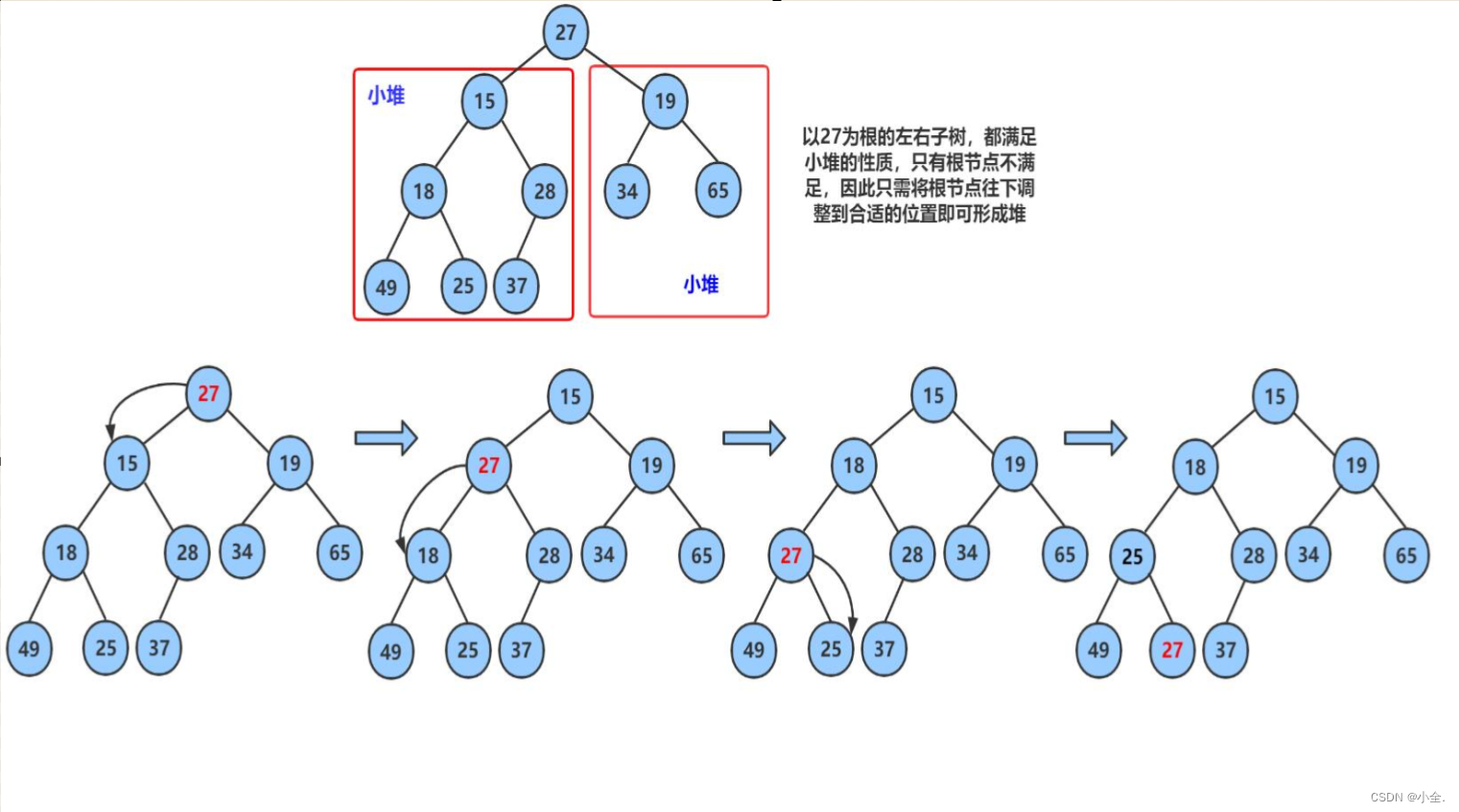
public void shiftDown(int[] array, int parent) {// child先标记parent的左孩子，因为parent可能右左没有右int child = 2 * parent + 1;int size = array.length;while (child < size) {// 如果右孩子存在，找到左右孩子中较小的孩子,用child进行标记if(child+1 < size && array[child+1] < array[child]){child += 1;}// 如果双亲比其最小的孩子还小，说明该结构已经满足堆的特性了if (array[parent] <= array[child]) {break;}else{// 将双亲与较小的孩子交换int t = array[parent];array[parent] = array[child];array[child] = t;// parent中大的元素往下移动，可能会造成子树不满足堆的性质，因此需要继续向下调整parent = child;child = parent * 2 + 1;}}
}

注意：在调整以parent为根的二叉树时，必须要满足parent的左子树和右子树已经是堆了才可以向下调整。

杂度分析： 最坏的情况 即图示的情况， 从根一路比较到叶子，比较的次数为完全二叉树的高度，即时间复杂度为 O（log N）

2、堆的创建

那对于普通的序列{ 1,5,3,8,7,6 }，即根节点的左右子树不满足堆的特性，又该如何调整呢？

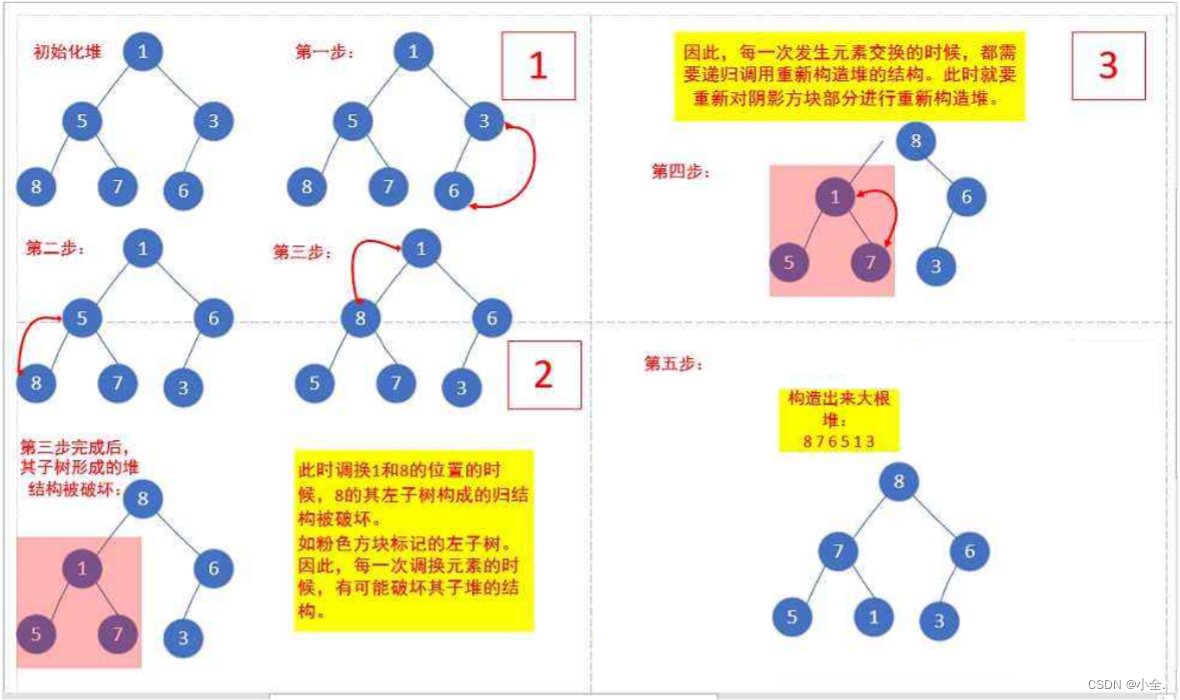
需要从倒数第一个非叶子结点开始，依次进行向下调整即可。

public static void createHeap(int[] array) {// 找倒数第一个非叶子节点，从该节点位置开始往前一直到根节点，遇到一个节点，应用向下调整int root = ((array.length-2)>>1);for (; root >= 0; root--) {shiftDown(array, root);}
}

3、建堆的时间复杂度

因为堆是完全二叉树，而满二叉树也是完全二叉树，此处为了简化使用满二叉树来证明(时间复杂度本来看的就是
近似值，多几个节点不影响最终结果)：

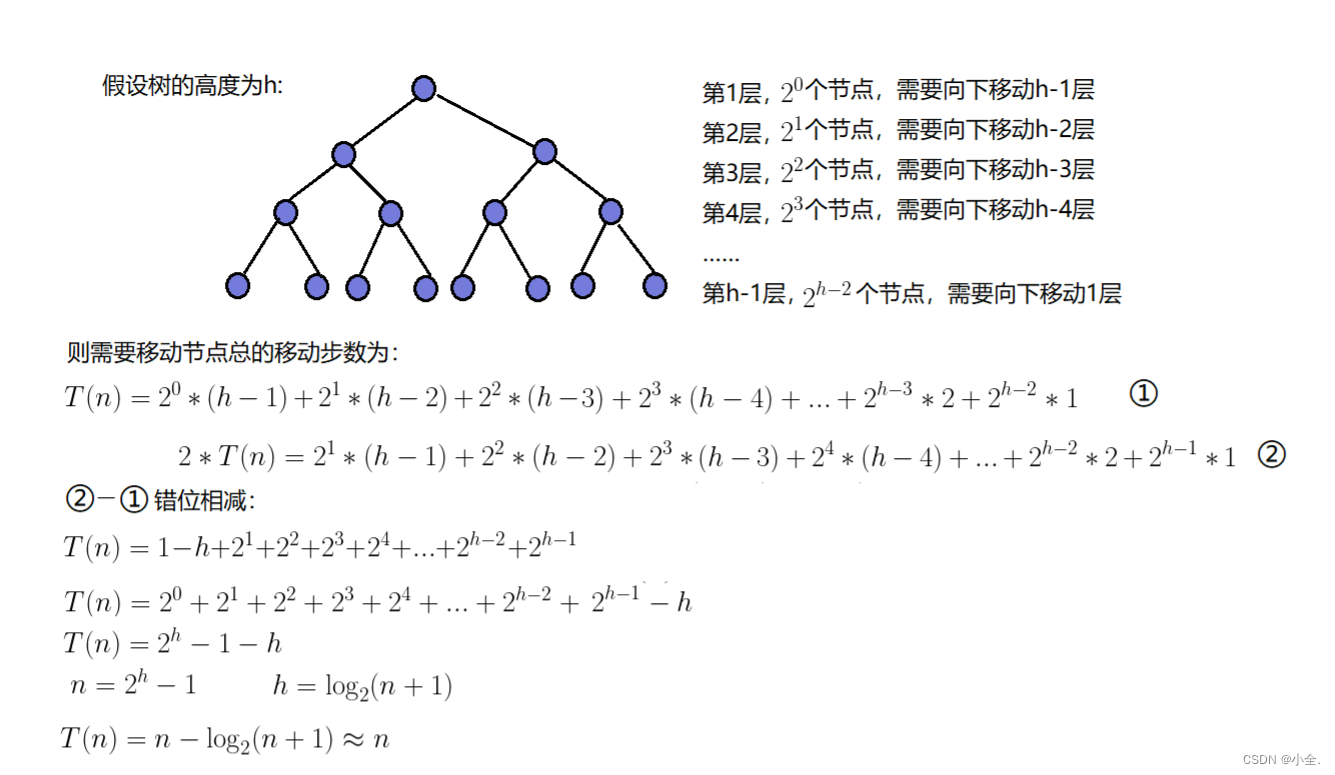
建堆的时间复杂度为O(N)。

四、堆的插入与删除

1、堆的插入

堆的插入总共需要两个步骤：

1. 先将元素放入到底层空间中(注意：空间不够时需要扩容)
2. 将最后新插入的节点向上调整，直到满足堆的性质

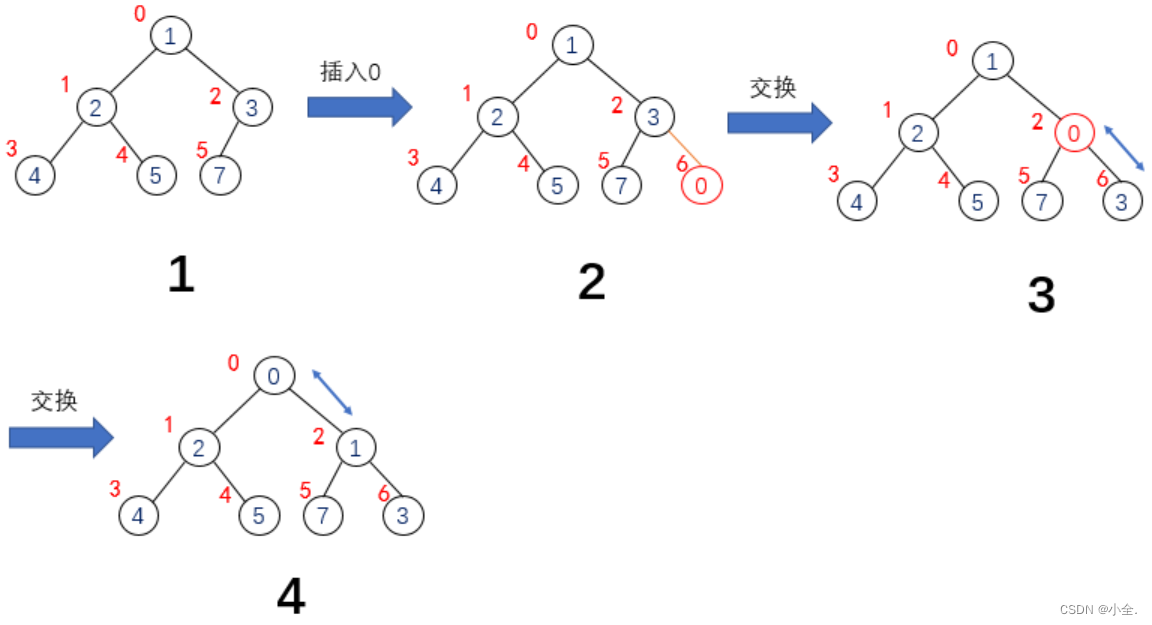
public void shiftUp(int child) {// 找到child的双亲int parent = (child - 1) / 2;while (child > 0) {// 如果双亲比孩子大，parent满足堆的性质，调整结束if (array[parent] > array[child]) {break;} else{// 将双亲与孩子节点进行交换int t = array[parent];array[parent] = array[child];array[child] = t;// 小的元素向下移动，可能到值子树不满足对的性质，因此需要继续向上调增child = parent;parent = (child - 1) / 1;}}
}

2、堆的删除

注意：堆的删除一定删除的是堆顶元素。具体如下：

1. 将堆顶元素对堆中最后一个元素交换
2. 将堆中有效数据个数减少一个
3. 对堆顶元素进行向下调整

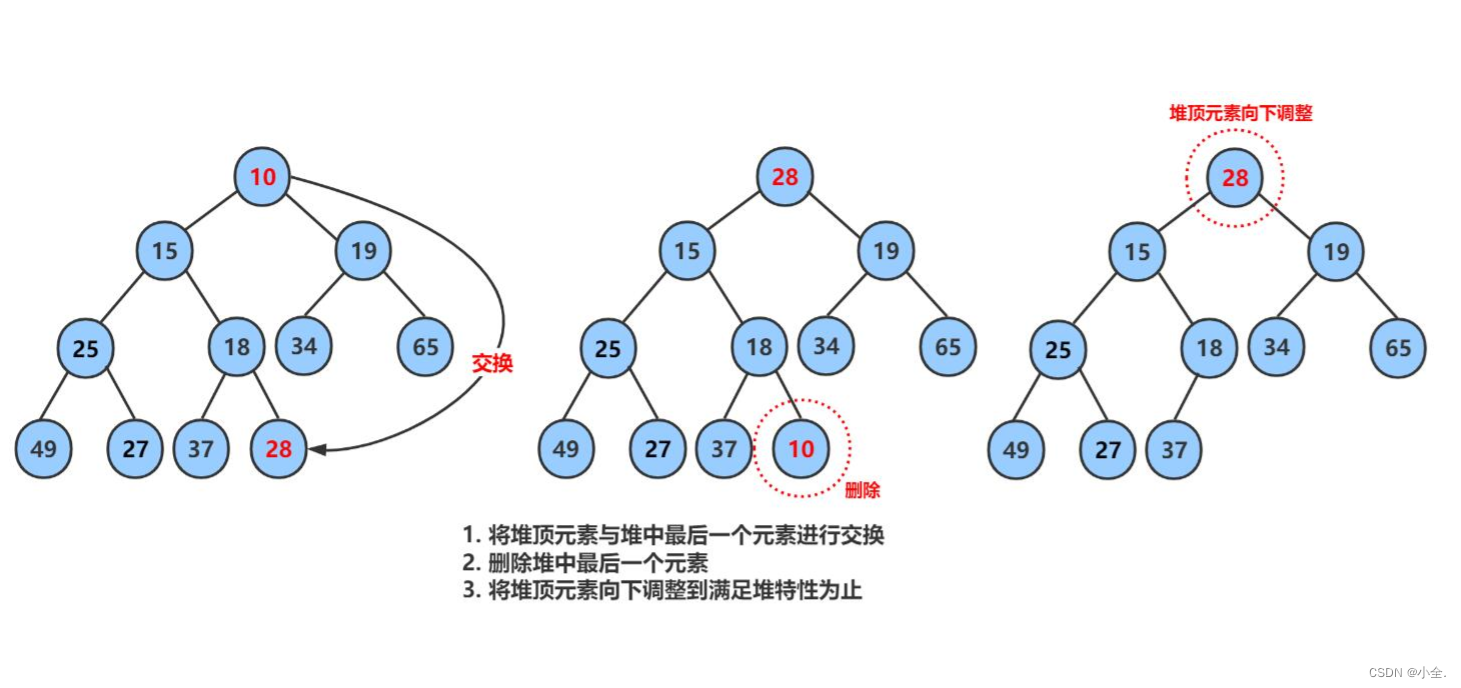
五、用堆模拟实现优先级队列

public class MyPriorityQueue {// 演示作用，不再考虑扩容部分的代码private int[] array = new int[100];private int size = 0;public void offer(int e) {array[size++] = e;shiftUp(size - 1);}public int poll() {int oldValue = array[0];array[0] = array[--size];shiftDown(0);return oldValue;}public int peek() {return array[0];}
}