蓝桥杯练习题——dp
五部曲(代码随想录)
1.确定 dp 数组以及下标含义
2.确定递推公式
3.确定 dp 数组初始化
4.确定遍历顺序
5.debug
入门题
1.斐波那契数

思路
1.f[i]:第 i 个数的值
2.f[i] = f[i - 1] + f[i - 2]
3.f[0] = 0, f[1] = 1
4.顺序遍历
5.记得特判 n == 0 的时候,因为初始化了 f[1]
class Solution {
public:int fib(int n) {if(n == 0) return n;vector<int> f(n + 1);f[0] = 0, f[1] = 1;for(int i = 2; i <= n; i++) f[i] = f[i - 1] + f[i - 2];return f[n];}
};
2.爬楼梯

思路
每次可以从下面一个台阶或者下面两个台阶处上来
1.f[i]:爬到第 i 阶楼梯有多少种方法
2.f[i] = f[i - 1] + f[i - 2]
3.f[0] = 1, f[1] = 1
4.顺序遍历
class Solution {
public:int climbStairs(int n) {vector<int> f(n + 1);f[0] = 1, f[1] = 1;for(int i = 2; i <= n; i++) f[i] = f[i - 1] + f[i - 2];return f[n];}
};
3.使用最小花费爬楼梯

思路
可以从 0 或 1 处开始爬楼梯,需要爬到第 n 阶楼梯
1.f[i]:爬到第 i 阶楼梯需要的最小花费
2.f[i] = min(f[i - 1] + cost[i - 1], f[i - 2] + cost[i - 2)
3.f[0] = 0, f[1] = 0
4.顺序遍历
class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {int n = cost.size();vector<int> f(n + 1);f[0] = 0, f[1] = 0;for(int i = 2; i <= n; i++){f[i] = min(f[i - 1] + cost[i - 1], f[i - 2] + cost[i - 2]);}return f[n];}
};
4.不同路径

思路
1.f[i][j]: 走到 (i, j) 总共的路径
2.f[i][j] = f[i - 1][j] + f[i][j - 1]
3.f[i][1] = 1, f[1][i] = 1
4.顺序遍历
class Solution {
public:int uniquePaths(int m, int n) {vector<vector<int>> f(n + 1, vector<int>(m + 1));for(int i = 0; i <= n; i++) f[i][1] = 1;for(int i = 0; i <= m; i++) f[1][i] = 1;for(int i = 2; i <= n; i++){for(int j = 2; j <= m; j++){f[i][j] = f[i - 1][j] + f[i][j - 1];}}return f[n][m];}
};
5.不同路径 II
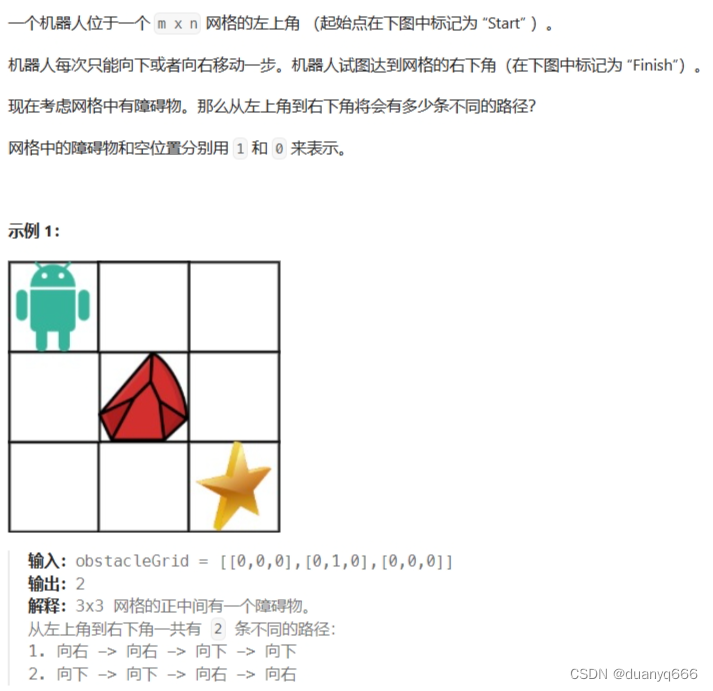
思路
1.f[i][j]: 走到 (i, j) 总共的路径
2.f[i][j] = f[i - 1][j] + f[i][j - 1]
3.f[i][0] = 1, f[0][i] = 1, 其他 = 0
4.顺序遍历
class Solution {
public:int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {int n = obstacleGrid.size();int m = obstacleGrid[0].size();vector<vector<int>> f(n, vector<int>(m, 0));for(int i = 0; i < n && !obstacleGrid[i][0]; i++) f[i][0] = 1;for(int i = 0; i < m && !obstacleGrid[0][i]; i++) f[0][i] = 1;for(int i = 1; i < n; i++){for(int j = 1; j < m; j++){if(!obstacleGrid[i][j]){f[i][j] = f[i - 1][j] + f[i][j - 1];}}}return f[n - 1][m - 1];}
};
6.整数拆分

思路
1.f[i]: 拆数字 i 可得到的最大乘积
2.拆分成 j * (i - j) 或 j * f[i - j],f[i] = max(f[i], max(j * (i - j), j * [i - j]))
3.f[0] = 0, f[1] = 1
4.顺序遍历
class Solution {
public:int integerBreak(int n) {vector<int> f(n + 1);f[0] = 0, f[1] = 1;for(int i = 2; i <= n; i++){for(int j = 0; j < i; j++){f[i] = max(f[i], max(j * (i - j), j * f[i - j]));}}return f[n];}
};
7.不同的二叉搜索树
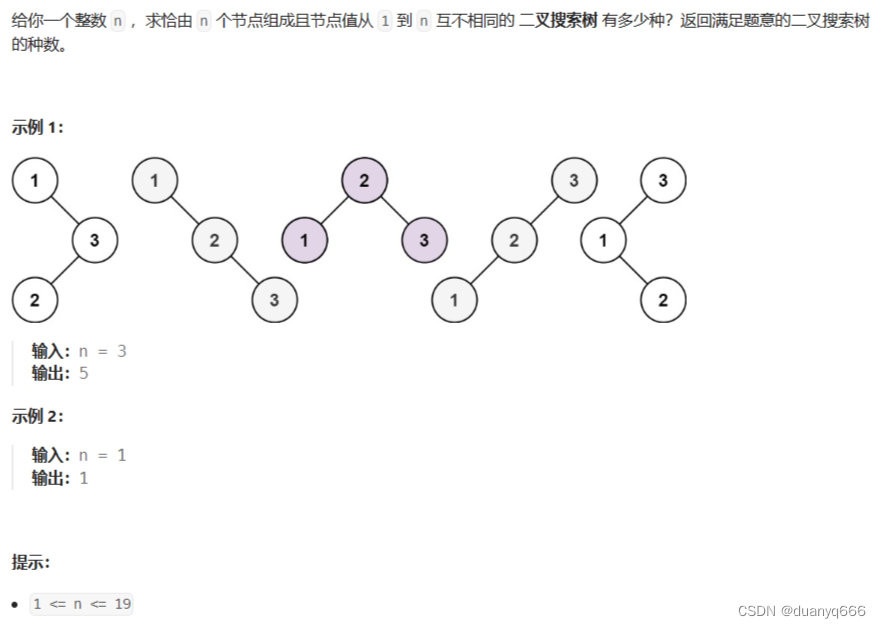
思路
dp[3],就是 元素1为头结点搜索树的数量 + 元素2为头结点搜索树的数量 + 元素3为头结点搜索树的数量
元素1为头结点搜索树的数量 = 右子树有2个元素的搜索树数量 * 左子树有0个元素的搜索树数量
元素2为头结点搜索树的数量 = 右子树有1个元素的搜索树数量 * 左子树有1个元素的搜索树数量
元素3为头结点搜索树的数量 = 右子树有0个元素的搜索树数量 * 左子树有2个元素的搜索树数量
有2个元素的搜索树数量就是dp[2]。
有1个元素的搜索树数量就是dp[1]。
有0个元素的搜索树数量就是dp[0]。
所以dp[3] = dp[2] * dp[0] + dp[1] * dp[1] + dp[0] * dp[2]
dp[i] += dp[以j为头结点左子树节点数量] * dp[以j为头结点右子树节点数量]
1.f[i]: 由 1 到 i 个节点的二叉搜索树个数
2.f[i] += f[j - 1] * f[i - j]
3.f[0] = 1
4.顺序遍历
class Solution {
public:int numTrees(int n) {vector<int> f(n + 1);f[0] = 1;for(int i = 1; i <= n; i++){for(int j = 1; j <= i; j++){f[i] += f[j - 1] * f[i - j];}}return f[n];}
};
背包问题
1.01背包问题

思路
1.f[i][j]: 前 i 个物品在容量为 j 的情况下的最大价值
2.f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i])
3.全部 = 0
4.顺序遍历
#include<iostream>
using namespace std;
const int N = 1e3 + 10;
int f[N][N], v[N], w[N];
int n, m;int main(){scanf("%d%d", &n, &m);for(int i = 1; i <= n; i++) scanf("%d%d", &v[i], &w[i]);for(int i = 1; i <= n; i++){for(int j = 0; j <= m; j++){// 不选f[i][j] = f[i - 1][j];// 选if(v[i] <= j) f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]);}}printf("%d", f[n][m]);return 0;
}// 滚动数组优化
#include<iostream>
using namespace std;
const int N = 1e3 + 10;
int f[N], v[N], w[N];
int n, m;int main(){scanf("%d%d", &n, &m);for(int i = 1; i <= n; i++) scanf("%d%d", &v[i], &w[i]);for(int i = 1; i <= n; i++){for(int j = m; j >= v[i]; j--){f[j] = max(f[j], f[j - v[i]] + w[i]);}}printf("%d", f[m]);return 0;
}
2.分割等和子集

思路
分割成两个等和子集,即找到是否存在和为 sum / 2 的子集,转化为 01 背包,背包容量为 sum / 2
1.f[j]: 背包容量为 i,放入物品后的最大重量
2.f[j] = max(f[j], f[j - nums[i]] + nums[i])
3.全部 = 0
4.倒序遍历
class Solution {
public:bool canPartition(vector<int>& nums) {int n = nums.size(), sum = 0;for(int i = 0; i < n; i++) sum += nums[i];if(sum % 2) return false;vector<int> f(10001, 0);for(int i = 0; i < n; i++){for(int j = sum / 2; j >= nums[i]; j--){f[j] = max(f[j], f[j - nums[i]] + nums[i]);if(f[j] == sum / 2) return true;}}return false;}
};
3.最后一块石头的重量 II

思路
尽可能分成两堆重量相同,使得相撞后重量最小
1.f[j]: 容量为 j 的背包,最大价值
2.f[j] = max(f[j], f[j - stones[i]] + stones[i])
3.全部 = 0
4.倒序遍历
class Solution {
public:int lastStoneWeightII(vector<int>& stones) {int n = stones.size(), sum = 0;for(int i = 0; i < n; i++) sum += stones[i];vector<int> f(1501, 0);for(int i = 0; i < n; i++){for(int j = sum / 2; j >= stones[i]; j--){f[j] = max(f[j], f[j - stones[i]] + stones[i]);}}return (sum - f[sum / 2]) - f[sum / 2];}
};
4.目标和

思路
pos - neg = tar 得 pos - (sum - pos) = tar 得 pos = (sum + tar) / 2
转换为背包容量为 pos,有多少种情况装满
无解的情况:pos 为奇数,tar 的绝对值大于 sum
只要搞到 nums[i],凑成 f[j] 就有 f[j - nums[i]] 种方法。
例如:f[j],j 为5,
已经有一个1(nums[i])的话,有 f[4]种方法 凑成 容量为5的背包。
已经有一个2(nums[i])的话,有 f[3]种方法 凑成 容量为5的背包。
已经有一个3(nums[i])的话,有 f[2]中方法 凑成 容量为5的背包
已经有一个4(nums[i])的话,有 f[1]中方法 凑成 容量为5的背包
已经有一个5(nums[i])的话,有 f[0]中方法 凑成 容量为5的背包
那么凑整 f[5] 有多少方法呢,也就是把 所有的 f[j - nums[i]] 累加起来。
1.f[j]:填满 j 背包有多少种情况
2.f[j] += f[j - nums[i]]
3.f[0] = 1,其他 = 0
4.倒序遍历
class Solution {
public:int findTargetSumWays(vector<int>& nums, int target) {int n = nums.size(), sum = 0;for(int i = 0; i < n; i++) sum += nums[i];if((sum + target) % 2 || abs(target) > sum) return 0;int pos = (sum + target) / 2;vector<int> f(pos + 1, 0);f[0] = 1;for(int i = 0; i < n; i++){for(int j = pos; j >= nums[i]; j--){f[j] += f[j - nums[i]];}}return f[pos];}
};
5.一和零

思路
可以等价为两个 01 背包,一个装 0,一个装 1
1.f[i][j]: 最多有 i 个 0 和 j 个 1 的最长子集大小
2.f[i][j] = max(f[i][j], f[i - zero][j - one] + 1)
3.全部 = 0
4.倒序遍历
class Solution {
public:int findMaxForm(vector<string>& strs, int m, int n) {vector<vector<int>> f(m + 1, vector<int>(n + 1, 0));for(auto str : strs){int zero = 0, one = 0;for(int i = 0; i < str.size(); i++){if(str[i] == '0') zero++;else one++; }for(int i = m; i >= zero; i--){for(int j = n; j >= one; j--){f[i][j] = max(f[i][j], f[i - zero][j - one] + 1);}}}return f[m][n];}
};
相关文章:

蓝桥杯练习题——dp
五部曲(代码随想录) 1.确定 dp 数组以及下标含义 2.确定递推公式 3.确定 dp 数组初始化 4.确定遍历顺序 5.debug 入门题 1.斐波那契数 思路 1.f[i]:第 i 个数的值 2.f[i] f[i - 1] f[i - 2] 3.f[0] 0, f[1] 1 4.顺序遍历 5.记得特判 …...

kotlin基础语法
1.变量 var a:Int 2 //声明类型的可变变量 var b 3 //代码推测可变变量类型 val c 6 //代码推测不可变常量类型 var d:String?null //可为null的String类型的可变变量 latei…...

淘宝天猫商家爬虫工具 电商采集软件使用教程
介绍: 淘宝和天猫是中国最大的电商平台之一,商家在这里销售各种商品。在市场竞争激烈的环境下,了解竞争对手的商品信息和价格变化对于电商运营来说非常重要。本文将介绍如何使用Python编写一个简单的淘宝天猫商家爬虫工具,以获取商…...

建库建表时,最容易忽略的10个细节
大家使用 DolphinDB 创建数据库和表时,有时对于分区列、分区类型和排序列的选择并不十分清晰。如果不加注意,可能导致查询速度变慢、数据丢失或插入错误等问题。合理地设置分区列、排序列和分区类型,有助于加快查询速度,减少内存使…...
)
【基础知识】什么是 PPO(Proximal Policy Optimization,近端策略优化)
什么是 PPO(Proximal Policy Optimization,近端策略优化) PPO(Proximal Policy Optimization,近端策略优化)是一种强化学习算法,由John Schulman等人在2017年提出。PPO属于策略梯度方法&#x…...

程序员如何选择职业赛道?
程序员如何选择职业赛道? 程序员的职业赛道就像是一座迷宫,充满了各种各样的岔路口。每个岔路口都代表着不同的方向,不同的技术领域,不同的职业发展道路。 前端开发 前端开发就像迷宫中的美丽花园,它是用户与网站或应…...
[LeetBook]【学习日记】寻找和为指定数字的连续数字
题目 文件组合 待传输文件被切分成多个部分,按照原排列顺序,每部分文件编号均为一个 正整数(至少含有两个文件)。传输要求为:连续文件编号总和为接收方指定数字 target 的所有文件。请返回所有符合该要求的文件传输组…...

阿里云中小企业扶持权益
为企业提供云资源和技术服务,助力企业开启智能时代创业新范式。阿里云推出中小企业扶持权益 上云必备,助力企业长期低成本用云 一、ECS-经济型e实例、ECS u1实例活动规则 活动时间 2023年10月31日0点0分0秒至2026年3月31日23点59分59秒 活动对象 同时满…...

2核4g服务器能支持多少人访问?并发数性能测评
2核4g服务器能支持多少人访问?支持80人同时访问,阿腾云使用阿里云2核4G5M带宽服务器,可以支撑80个左右并发用户。阿腾云以Web网站应用为例,如果视频图片媒体文件存储到对象存储OSS上,网站接入CDN,还可以支持…...

Anthropic官宣Claude3:建立大模型 推理、数学、编码和视觉等方面 新基准
文章目录 1. product2. Main2.1 核心能力2.2 打榜表现 3. My thoughtsReference Claude 3 在推理、数学、编码、多语言理解和视觉方面,全面超越GPT-4在内的所有大模型,重新树立大模型基准。 1. product https://claude.ai/ 国内暂不能使用,…...
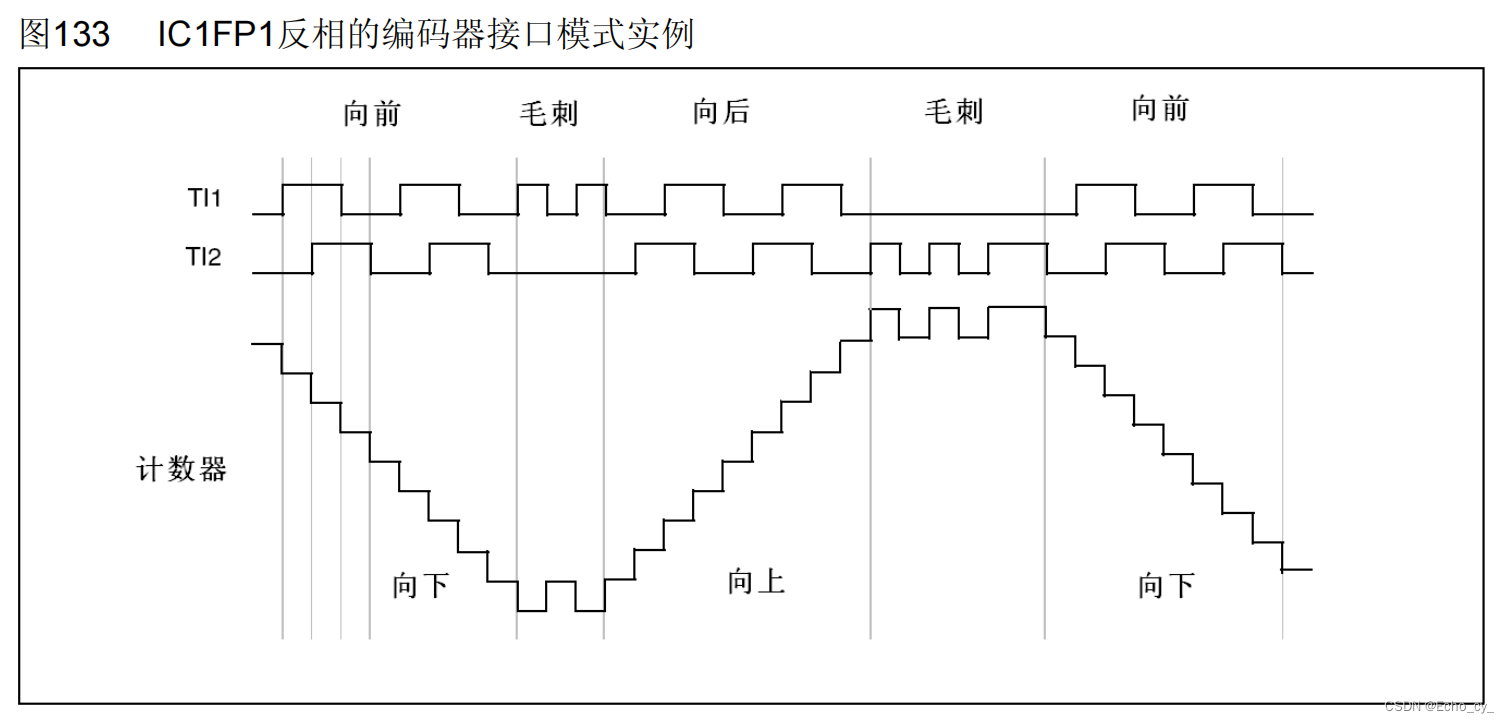
STM32 TIM编码器接口
单片机学习! 目录 文章目录 前言 一、编码器接口简介 1.1 编码器接口作用 1.2 编码器接口工作流程 1.3 编码器接口资源分布 1.4 编码器接口输入引脚 二、正交编码器 2.1 正交编码器功能 2.2 引脚作用 2.3 如何测量方向 2.4 正交信号优势 2.5 执行逻辑 三、编码器定时…...

Jupyter Notebook的安装和使用(windows环境)
一、jupyter notebook 安装 前提条件:安装python环境 安装python环境步骤: 1.下载官方python解释器 2.安装python 3.命令行窗口敲击命令pip install jupyter 4.安装jupyter之后,直接启动命令jupyter notebook,在默认浏览器中打开jupyte…...
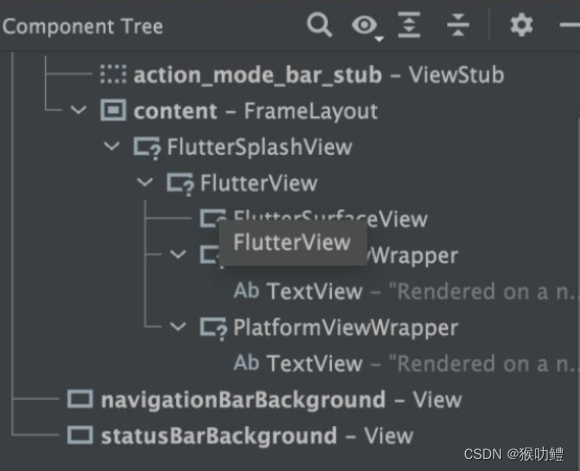
Platformview在iOS与Android上的实现方式对比
Android中早期版本Platformview的实现基于Virtual Display。VirtualDisplay方案的原理是,先将Native View绘制到虚显,然后Flutter通过从虚显输出中获取纹理并将其与自己内部的widget树进行合成,最后作为Flutter在 Android 上更大的纹理输出的…...
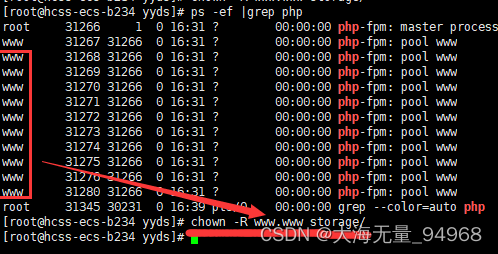
使用lnmp环境部署laravel框架需要注意的点
1,上传项目文件后,需要chmod -R 777 storage授予文件权限,不然会报错file_put_contents(/): failed to open stream: Permission denied。 如果后面还是报错没有权限的话,就执行ps -ef |grep php查询php运行用户。然后执行chown …...

AI-RAN联盟在MWC24上正式启动
AI-RAN联盟在MWC24上正式启动。它的logo是这个样的: 2月26日,AI-RAN联盟(AI-RAN Alliance)在2024年世界移动通信大会(MWC 2024)上成立。创始成员包括亚马逊云科技、Arm、DeepSig、爱立信、微软、诺基亚、美…...

Reactor详解
目录 1、快速上手 介绍 2、响应式编程 2.1. 阻塞是对资源的浪费 2.2. 异步可以解决问题吗? 2.3.1. 可编排性与可读性 2.3.2. 就像装配流水线 2.3.3. 操作符(Operators) 2.3.4. subscribe() 之前什么都不会发生 2.3.5. 背压 2.3.6. …...

实践航拍小目标检测,基于YOLOv5全系列【n/s/m/l/x】参数模型开发构建无人机航拍场景下的小目标检测识别分析系统
关于无人机相关的场景在我们之前的博文也有一些比较早期的实践,感兴趣的话可以自行移步阅读即可: 《deepLabV3Plus实现无人机航拍目标分割识别系统》 《基于目标检测的无人机航拍场景下小目标检测实践》 《助力环保河道水质监测,基于yolov…...

分布式数据库中全局自增序列的实现
自增序列广泛使用于数据库的开发和设计中,用于生产唯一主键、日志流水号等唯一ID的场景。传统数据库中使用Sequence和自增列的方式实现自增序列的功能,在分布式数据库中兼容Oracle和MySQL等传统数据库语法,也是基于Sequence和自增列的方式实现…...
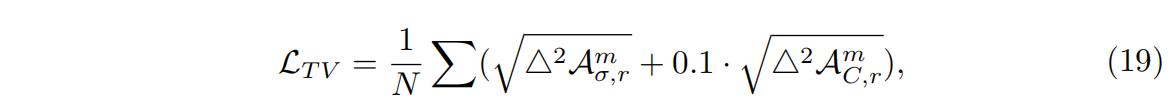
【论文阅读】TensoRF: Tensorial Radiance Fields 张量辐射场
发表于ECCV2022. 论文地址:https://arxiv.org/abs/2203.09517 源码地址:https://github.com/apchenstu/TensoRF 项目地址:https://apchenstu.github.io/TensoRF/ 摘要 本文提出了TensoRF,一种建模和重建辐射场的新方法。不同于Ne…...

深入了解 Android 中的 FrameLayout 布局
FrameLayout 是 Android 中常用的布局之一,它允许子视图堆叠在一起,可以在不同位置放置子视图。在这篇博客中,我们将详细介绍 FrameLayout 的属性及其作用。 <FrameLayout xmlns:android"http://schemas.android.com/apk/res/androi…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

API网关Kong的鉴权与限流:高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中,API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关,Kong凭借其插件化架构…...
