【C++】十大排序算法之 归并排序 快速排序
本次介绍内容参考自:十大经典排序算法(C++实现) - fengMisaka - 博客园 (cnblogs.com)
排序算法是《数据结构与算法》中最基本的算法之一。
十种常见排序算法可以分为两大类:
- 比较类排序:通过比较来决定元素间的相对次序,时间复杂度为 O(nlogn)~O(n²)。
- 非比较类排序:不通过比较来决定元素间的相对次序,其时间复杂度可以突破 O(nlogn),以线性时间运行。
【十大经典排序算法分类】

【十大经典排序算法的复杂度分析】

名词解释:
-
时间/空间复杂度:描述一个算法执行时间/占用空间与数据规模的增长关系。
-
n:待排序列的个数。
-
k:“桶”的个数(上面的三种非比较类排序都是基于“桶”的思想实现的)。
-
In-place:原地算法,指的是占用常量内存,不占用额外内存。即空间复杂度为 O(1) 。
-
Out-place:非原地算法,占用额外内存。
-
稳定性:假设待排序列中两元素相等,排序前后这两个相等元素的相对位置不变,则认为是稳定的。
一、归并排序(Merge-Sort)
归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为 2- 路归并。
1.1、算法描述
- 把长度为 n 的输入序列分成两个长度为 n/2 的子序列;
- 对这两个子序列分别采用归并排序;
- 将两个排序好的子序列合并成一个最终的排序序列。
1.2、动图演示

归并排序动图演示
1.3、C++编码
/**
* @version Copyright (c) 2024 NCDC, Servo。 Unpublished - All rights reserved
* @file MergeSort.hpp
* @brief 归并排序
* @autor 写代码的小恐龙er
* @date 2024/03/05
*/// 【分治法】 & 【递归法】
// 时间复杂度O(n * log n)
// 空间复杂度O(n)/* 将 arr[l..m] 和 arr[m+1..r] 归并 */
void Merge(int arr[], int l, int m, int r) {// 将arr数组分成左右两个 有序序列 再合并在一起int leftSize= m - l + 1; // 包含中间的元素int rightSize= r - m;vector<int> left(leftSize, 0);vector<int> right(rightSize, 0);int i, j, k;// 以 M 为分割线,把原数组分成左右子数组for (i = l; i <= m; i++) left[i - l] = arr[i];for (i = m + 1; i <= r; i++) right[i - m - 1] = arr[i];// 再合并成一个有序数组(从两个序列中选出最小值依次插入)i = 0; j = 0; k = L;while (i < leftSize && j < rightSize) {arr[k++] = left[i] < right[j] ? left[i++] : right[j++];}// 对于超出的部分进行单独填充while (i < leftSize) arr[k++] = left[i++];while (j < rightSize) arr[k++] = right[j++];
}void MergeSort(int arr[], int l, int r) {// 终止条件if (l == r) return;// 将 arr[l..r] 平分为 arr[l..m] 和 arr[m+1..r]int m = (l + r) / 2;// 分别递归地将子序列排序为有序数列MergeSort(arr, l, m);MergeSort(arr, m + 1, r);// 将两个排序后的子序列再归并到 arrMerge(arr, l, m, r);
}1.4 、算法分析
归并排序在实现上,通常采用 Out-place 排序(即需用到 O(n) 的额外空间的排序),在排序过程中属于稳定的排序算法,其时间复杂度均为O(n * log n)。在算法实现上采用了分治法与递归思想。
二、快速排序(Quick Sort)
快速排序(Quick Sort),是冒泡排序的改进版,之所以“快速”,是因为使用了分治法。它也属于交换排序,通过元素之间的位置交换来达到排序的目的。
基本思想:通过一趟排序将待排记录分隔成独立的两部分,其中一部分记录的关键字均比另一部分的关键字小,则可分别对这两部分记录继续进行排序,以达到整个序列有序。
2.1 、算法描述
- 从数列中挑出一个元素,称为 “基准”(pivot);
- 重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作;
- 递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序。
2.2 、动图演示
快速排序动图演示
2.3、C++编码
/**
* @version Copyright (c) 2024 NCDC, Servo。 Unpublished - All rights reserved
* @file QuickSort.hpp
* @brief 快速排序
* @autor 写代码的小恐龙er
* @date 2024/03/05
*/// 【分治法】 & 【递归法】
// 时间复杂度O(n * log n)
// 空间复杂度O(log n)void QuickSort(int *arr[], int begin, int end)
{ // 终止条件if (begin > end) // 递归,直到start = end为止return;// 基准数int pivot = arr[begin]; int i = begin;int j = end;while (i != j){// 从右向左找比基准数小的数 (要先从右边开始找)while (arr[j] >= pivot && i < j) j--;// 从左向右找比基准数大的数while (arr[i] <= pivot && i < j) i++;if (i < j){// 交换两个数在数组中的位置int temp = arr[i];arr[i] = arr[j];arr[j] = temp;}}// 最终将基准数归位arr[begin] = arr[i];arr[i] = pivot;// 递归处理QuickSort(arr, begin, i - 1); // 继续处理左边的,这里是一个递归的过程QuickSort(arr, i + 1, end); // 继续处理右边的 ,这里是一个递归的过程
} 2.4 、算法分析
快速排序是不稳定排序,之所比较快,是因为相比冒泡排序,每次交换是跳跃式的。每次排序的时候设置一个基准点,将小于等于基准点的数全部放到基准点的左边,将大于等于基准点的数全部放到基准点的右边。这样在每次交换的时候就不会像冒泡排序一样每次只能在相邻的数之间进行交换,交换的距离就大的多了。因此总的比较和交换次数就少了,速度自然就提高了。当然在最坏的情况下,仍可能是相邻的两个数进行了交换。因此快速排序的最差时间复杂度和冒泡排序是一样的都是 O(n²),它的平均时间复杂度为 O(n * log n)。和归并排序一样,其在算法实现上采用了分治法与递归思想。
相关文章:

【C++】十大排序算法之 归并排序 快速排序
本次介绍内容参考自:十大经典排序算法(C实现) - fengMisaka - 博客园 (cnblogs.com) 排序算法是《数据结构与算法》中最基本的算法之一。 十种常见排序算法可以分为两大类: 比较类排序:通过比较来决定元素间的相对次序…...

x-pack的破解方式和免费jar包!!可直接用!!
原理介绍 我们平时为es安装x-pack组件,用elasticsearch-plugin install x-pack ,安装成功后。 1.cd $es目录/pulgins/x-pack 里面有一个x-pack-5.6.2.jar ,将jar包反编译,然后将里面的licence的程序改下。再编译成jar包。 2…...

最新版本,Midjourney保姆级教程!
一、认识Midjourney 1.1、MidJourney是什么? 随着ChatGPT的横空出世,人类正式迈入AI元年,其中MidJourney便是AI绘图工具,它能根据用户输入的文字描述(提示词)生成绘画作品,不管是灵动的人物&a…...

Android中的几种定位方式调用详解
目前,移动端大致通过三种方式来进行设备定位:GPS、基站、wifi。本文就详细的讲解一下这几种定位方式和实现方法。 前言 android中我们一般使用LocationManager来获取位置信息,这里面有四中provider: public static final Strin…...
【软件测试】接口调不通排查分析+常遇面试题总结
目录:导读 前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜) 前言 1、接口调不通&am…...
)
c++基础学习第三天(指针,结构体)
c基础学习第三天(指针,结构体) 文章目录 1、指针1.1、指针的基本概念1.2、指针变量的定义和使用1.3、 指针所占内存空间1.4、空指针和野指针1.5、 const修饰指针1.5.1、const修饰指针-常量指针1.5.2、const修饰常量-指针常量1.5.3、const即修…...

【数仓】zookeeper软件安装及集群配置
相关文章 【数仓】基本概念、知识普及、核心技术【数仓】数据分层概念以及相关逻辑【数仓】Hadoop软件安装及使用(集群配置)【数仓】Hadoop集群配置常用参数说明 一、环境准备 准备3台虚拟机 Hadoop131:192.168.56.131Hadoop132ÿ…...
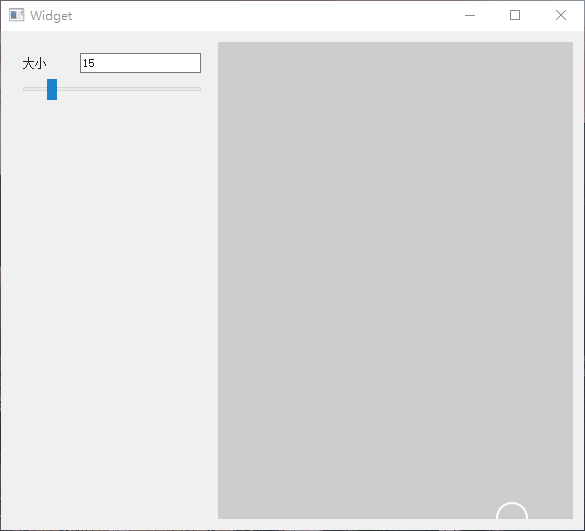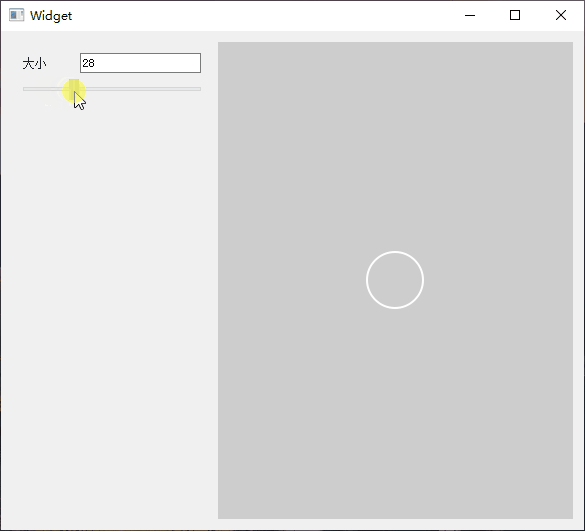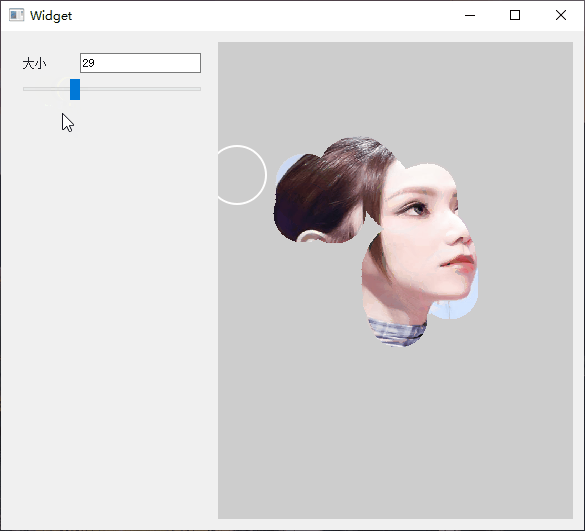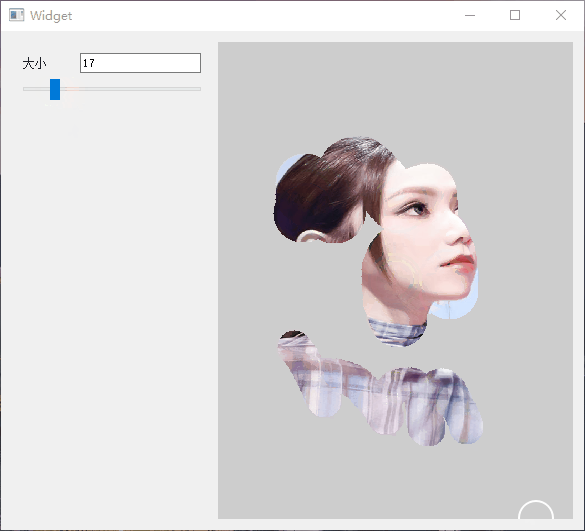
Qt 实现橡皮擦拭显示图片
1.简介 在一些游戏中看见类似解密破案的效果,使用手触摸去擦拭图片上的灰尘,然后显示最终的图片,所以也想试试Qt实现的效果。大家有自己想做的效果,都可以尝试。 以下是效果展示图。 可以控制橡皮擦的大小,进行擦拭…...

Vue3+Element-Plus中ELMessage样式丢失处理
Vu3Element-Plus项目中,element-plus使用按需引入有时会出现样式失效和在vscode中使用会报错[找不到名称“ElMessage”。ts(2304)]错误 ELMessage弹框样式丢失处理方法 使用按需引入就不能手动再引入 import { ElMessage } from "element-plus";ElMessage.success…...
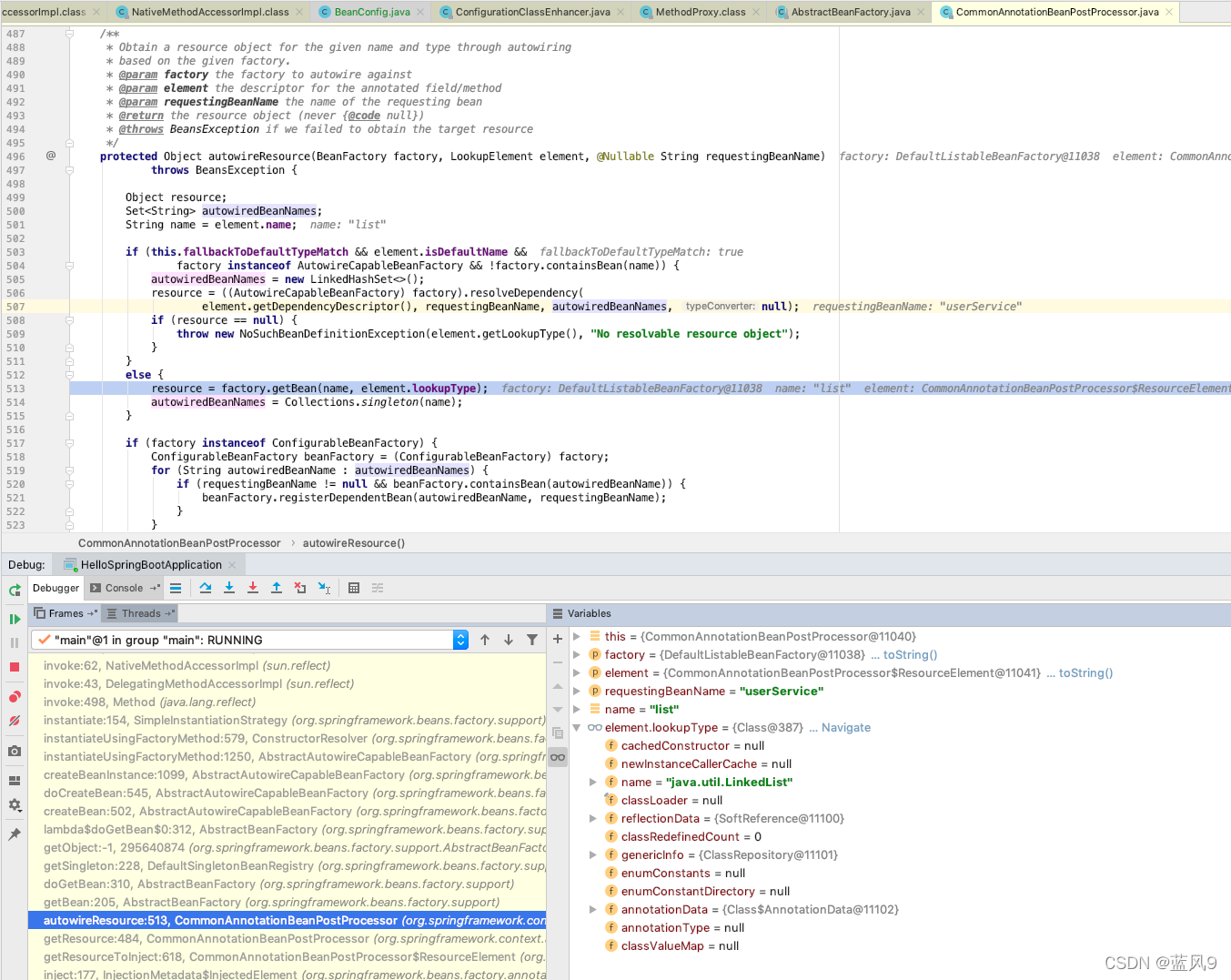
97 spring 中的泛型类型注入
前言 呵呵 同样是 最近同事碰到的一个问题 他不太懂 英语, 看到的说明是 缺少一个 RedisTemplate 的实例, 但是找到了一个 RedisTemplate 的实例 呵呵 和我这里 spring 版本似乎是不太一样, 错误信息 有一些差异 以下环境基于 jdk8 spring-5.0.4-RELEASE 测试用例 BeanCon…...
C++设计模式
单例模式 单例模式保证一个类只能创建一个对象,并提供全局访问点。通常用于全局共享例如日志、数据库连接池等。 Lazy Initialization 优点:需要时才初始化,节省空间 缺点:线程不安全 class Singleton{ private:static Singlet…...

反向代购业务系统|无货源代购中国商品|反向海淘代购系统
什么是淘宝代购 淘宝代购是近年兴起的一种购物模式,是帮国外客户购买中国商品。主要是通过万邦科技的外贸代购模式,把淘宝、 天猫等电商平台的全站商品通过API接入到你的网站上,瞬间就可以架设一个有数亿产品的大型网上商城,而且…...
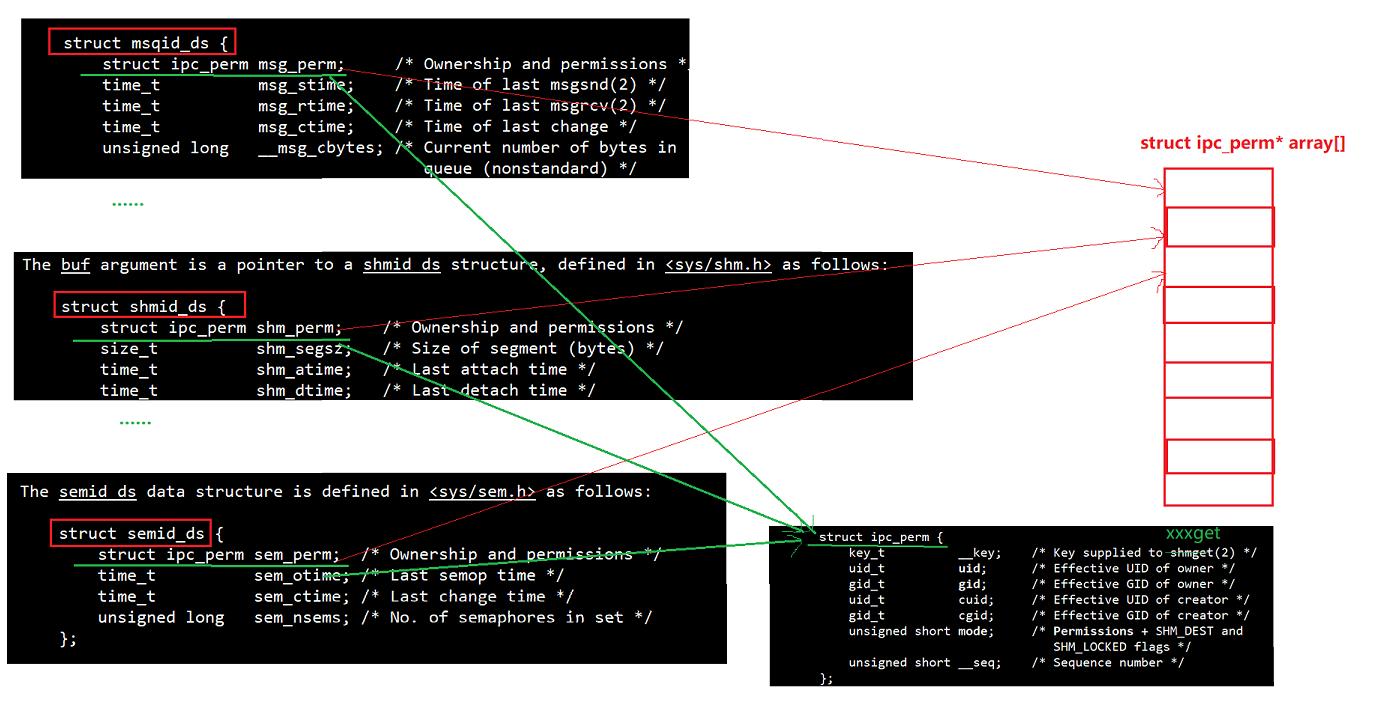
Linux 进程间通信
目录 管道 匿名管道(pipe) 有名管道(fifo) 小结 共享内存 消息队列 信号量 System V IPC的结构设计 Posix与System V的关系 管道 匿名管道(pipe) 我们知道,在Linux中通过fork创建的子…...
hippy 调试demo运行联调-mac环境准备篇
适用对于终端编译环境不熟悉的人看,仅mac端 hippy 调试文档官网地址 前提:请使用node16 联调预览效果图: 编译iOS Demo环境准备 未跑通,待补充 编译Android Demo环境准备 1、正常安装Android Studio 2、下载Android NDK&a…...

【golang】go module依赖的git tag被覆盖 如何处理 | 因测试产生大量的git tag 如何清除 最佳实践
一、场景 当我们把本地和远程git仓库的 tag全部删除,我们另外的项目依赖于这个被删除tag无法更新版本 如何处理? 如上图: 这里我创建了一个 v0.0.1 的tag,然后删除了这个tag,然后又创建了一个新的 v0.0.1的tag…...

Spring Cloud原理详解
Spring Cloud 是基于 Spring Boot 的微服务架构开发工具包,旨在帮助开发人员快速构建分布式系统中的一些常见模式,例如配置管理、服务发现、断路器、智能路由、微代理、控制总线、全局锁、领导选举、分布式会话和集群状态。Spring Cloud 是 Spring 生态系…...
力扣76. 最小覆盖子串(滑动窗口)
Problem: 76. 最小覆盖子串 文章目录 题目描述思路复杂度Code 题目描述 思路 1.定义两个map集合need和window(以字符作为键,对应字符出现的个数作为值),将子串t存入need中; 2.定义左右指针left、right均指向0ÿ…...

使用华为云云函数functiongraph
之前使用腾讯云serverless,但是突然开始收费了。所以改用functiongraph 首先登陆华为云。 目录 1.登录华为云 2.在控制台找到functiongraph并开通 3.添加依赖包: 3.1 制作依赖包 3.2引入依赖包 4.发送请求 4.1直接发送 4.1.1uri 4.1.2 请求头…...
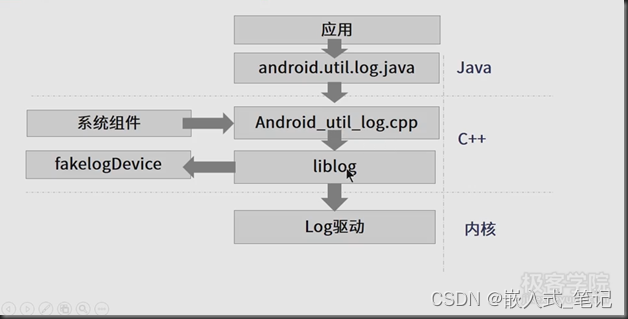
Android logcat系统
一 .logcat命令介绍 android log系统: logcat介绍 : logcat是android中的一个命令行工具,可以用于得到程序的log信息. 二.C/Clogcat访问接口 Android系统中的C/C日志接口是通过宏来使用的。在system/core/include/android/log.h定义了日志的级别: /…...

android 使用协程CoroutineScope 实现定时器
满足延迟执行、立即执行,每次任务间隔时长,总时长的任务 使用1 class TimeViewModel:Viewmodel(){//测试延迟5秒开始执行任务,然后每隔1秒执行1次,总执行时间60秒fun testTime(){var startTime System.currentTimeMillis()log(…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...

FFmpeg avformat_open_input函数分析
函数内部的总体流程如下: avformat_open_input 精简后的代码如下: int avformat_open_input(AVFormatContext **ps, const char *filename,ff_const59 AVInputFormat *fmt, AVDictionary **options) {AVFormatContext *s *ps;int i, ret 0;AVDictio…...

若依登录用户名和密码加密
/*** 获取公钥:前端用来密码加密* return*/GetMapping("/getPublicKey")public RSAUtil.RSAKeyPair getPublicKey() {return RSAUtil.rsaKeyPair();}新建RSAUti.Java package com.ruoyi.common.utils;import org.apache.commons.codec.binary.Base64; im…...

在golang中如何将已安装的依赖降级处理,比如:将 go-ansible/v2@v2.2.0 更换为 go-ansible/@v1.1.7
在 Go 项目中降级 go-ansible 从 v2.2.0 到 v1.1.7 具体步骤: 第一步: 修改 go.mod 文件 // 原 v2 版本声明 require github.com/apenella/go-ansible/v2 v2.2.0 替换为: // 改为 v…...
