C++模拟揭秘刘谦魔术,领略数学的魅力
新的一年又开始了,大家新年好呀~。在这我想问大家一个问题,有没有同学看了联欢晚会上刘谦的魔术呢?
这个节目还挺有意思的,它最出彩的不是魔术本身,而是小尼老师“念错咒语”而导致他手里的排没有拼在一起,当时还一度冲上了热搜。

这个魔术的背后其实是一个数学上的问题,它被称为约瑟夫问题,它是一个计算机科学和数学中的问题,在计算机编程的算法中,类似问题又称为约瑟夫环,又称“丢手绢问题”。
它的故事背景是这样的:
据说著名犹太历史学家Josephus(弗拉维奥·约瑟夫斯)有过以下的故事:在罗马人占领乔塔帕特后,39 个犹太人与Josephus及他的朋友躲到一个洞中,39个犹太人决定宁愿死也不要被敌人抓到,于是决定了一个自杀方式,41个人排成一个圆圈,由第1个人开始报数,每报数到第3人该人就必须自杀,然后再由下一个重新报数,直到所有人都自杀身亡为止。然而Josephus 和他的朋友并不想遵从。首先从一个人开始,越过k-2个人(因为第一个人已经被越过),并杀掉第k个人。接着,再越过k-1个人,并杀掉第k个人。这个过程沿着圆圈一直进行,直到最终只剩下一个人留下,这个人就可以继续活着。问题是,给定了和,一开始要站在什么地方才能避免被处决。Josephus要他的朋友先假装遵从,他将朋友与自己安排在第16个与第31个位置,于是逃过了这场死亡游戏。
在编程上的变形一般是这样的:
N个人围成一圈,从第一个开始报数,第M个出局,第M个出局之后它的下一个又从1开始报数,直到最后剩下一个,其余人都出局。例如N=6,M=5,被杀掉的顺序是:5,4,6,2,3。
给大家模拟一下这个过程:
(第一轮数字5出局,黑色字体的数字 代表n个人,红色字体代表每个人报的数字)
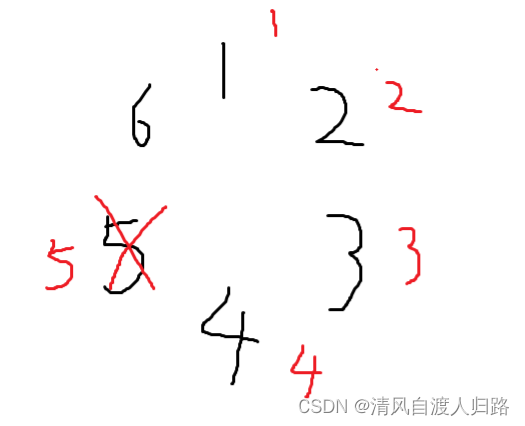
(第一轮数字5出局之后剩下5个数字,从数字6开始从1报数,依次顺下去就是数字4出局)

(第三轮数字依次往后报数,数字6出局)
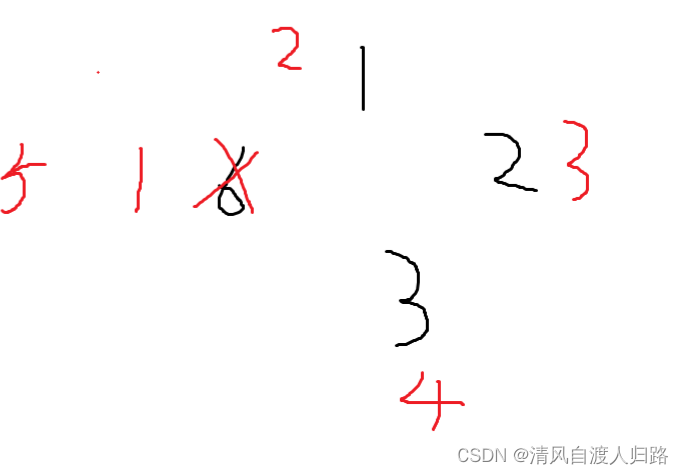
(第四轮数字2出局)

(第五轮数字3出局,第一个人胜利)

这是约瑟夫环问题的模拟过程,那现在大家一起来看一下程序怎么写。
第一种方法:递归
#include<iostream>
using namespace std;
int ysf(int n, int k, int i)//本函数是index=0开始
{if (i == 1)return (n+k-1) % n;if (i != 1)return (ysf(n - 1, k, i - 1) + k) % n;//即为去掉前面的人构成的新环的第i-1次
}
int main()
{int n, k;cin >> n >> k;for (int i = 1; i <= n; i++){cout << ysf(n, k, i)+1 << " ";//加1统一index=1开始}
}
第二种:队列
#include<iostream>
#include<queue>
using namespace std;
queue<int> res;
int n, k;
int main()
{cin >> n >> k;for (int i = 1; i <= n; i++){res.push(i);}int cnt = 0;while (!res.empty()){for (int i = 1; i <= k - 1; i++)//执行k-1次{res.push(res.front());//将队首元素放队尾去res.pop();}//循环结束后输出队首元素cout << res.front() << " ";res.pop();//出局}return 0;
}
第三种:循环链表
#include<iostream>
#include<cstdlib>
using namespace std;
typedef struct node
{int data;struct node* next;
}Node;
int n, k;
void Joseph_ring(int n, int k)
{//开始创建循环链表Node* head = NULL, * p = NULL, * r = NULL;//搞三个指针head = (Node*)malloc(sizeof(Node));//为head头指针申请一片空间((Node*)为强制类型转换为结构体变量指针)head->data = 1;head->next = NULL;p = head;//创建循环链表用,此时p和head指向头结点for (int i = 2; i <= n; i++)//创建剩下的n-1个结点(尾插法顺序插入){r = (Node*)malloc(sizeof(Node));r->data = i;r->next = NULL;p->next = r;p = r;}p->next = head;//首尾相接p = head;//恢复初始状态while (p->next != p)//结束条件是只剩下最后一个(当然用cnt计数也可以){for (int i = 1; i < k; i++){r = p;//用r保存该删结点的上一个结点p = p->next;}//循环结束后p指针的位置是该删结点的位置cout << p->data << " ";r->next = p->next;p = p->next;}//whlie循环结束后还剩最后一个结点要输出cout << p->data;
}
int main()
{cin >> n >> k;Joseph_ring(n,k);return 0;
}
好啦,同学们自己试一试吧~
相关文章:

C++模拟揭秘刘谦魔术,领略数学的魅力
新的一年又开始了,大家新年好呀~。在这我想问大家一个问题,有没有同学看了联欢晚会上刘谦的魔术呢? 这个节目还挺有意思的,它最出彩的不是魔术本身,而是小尼老师“念错咒语”而导致他手里的排没有拼在一起,…...

JAVA语言编写一个方法,两个Long参数传入,使用BigDecimal类,计算相除四舍五入保留2位小数返回百分数。
在Java中,你可以使用BigDecimal类来执行精确的浮点数计算,并且可以指定结果的小数位数。以下是一个方法,它接受两个Long类型的参数,并使用BigDecimal来计算它们的商,然后将结果四舍五入到两位小数,并返回一…...

SQL教学:掌握MySQL数据操作核心技能--DML语句基本操作之“增删改查“
大家好,今天我要给大家分享的是SQL-DML语句教学。DML,即Data Manipulation Language,也就是我们常说的"增 删 改 查",是SQL语言中用于操作数据库中数据的一部分。作为MySQL新手小白,掌握DML语句对于数据库数…...
【性能测试】Jmeter性能压测-阶梯式/波浪式场景总结(详细)
目录:导读 前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜) 前言 1、阶梯式场景&am…...
前端面试 跨域理解
2 实现 2-1 JSONP 实现 2-2 nginx 配置 2-2 vue 开发中 webpack自带跨域 2 -3 下载CORS 插件 或 chrome浏览器配置跨域 2-4 通过iframe 如:aaa.com 中读取bbb.com的localStorage 1)在aaa.com的页面中,在页面中嵌入一个src为bbb.com的iframe&#x…...
JetBrains TeamCity 身份验证绕过漏洞复现(CVE-2024-27198)
0x01 产品简介 JetBrains TeamCity是一款由JetBrains开发的持续集成和持续交付(CI/CD)服务器。它提供了一个功能强大的平台,用于自动化构建、测试和部署软件项目。TeamCity旨在简化团队协作和软件交付流程,提高开发团队的效率和产品质量。 0x02 漏洞概述 JetBrains Team…...

设计模式—单例模式
单例模式(Singleton Pattern)是一种常用的软件设计模式,其核心思想是确保一个类仅有一个实例,并提供一个全局访问点来获取这个实例。单例模式主要用于控制资源的访问,比如配置文件的读取,数据库的连接等&am…...

Android在后台读取UVC摄像头的帧数据流并推送
Android在后台读取UVC摄像头的帧数据流并推送 添加UvcCamera依赖库 使用原版的 saki4510t/UVCCamera 在预览过程中断开可能会闪退,这里使用的是 jiangdongguo/AndroidUSBCamera 中修改的版本,下载到本地即可。 https://github.com/jiangdongguo/AndroidU…...

vue单向数据流介绍
Vue.js 的单向数据流是其核心设计原则之一,也是 Vue 响应式系统的基础。在 Vue.js 中,数据流主要是单向的,从父组件流向子组件。这种设计有助于保持组件之间的清晰通信,减少不必要的复杂性和潜在的错误。 以下是 Vue 单向数据流的…...

OpenMMlab AI实战营第四期培训
OpenMMlab AI实战营第四期培训 OpenMMlab实战营第四次课2023.2.6学习参考一、什么是目标检测1.目标检测下游视觉任务2.图像分类 v.s. 目标检测 二、目标检测实现1.滑窗 Sliding Window2.滑窗的效率问题3.改进思路(1)消除滑窗中的重复计算(2&a…...

React轻松开发平台:实现高效、多变的应用开发范本
在当今快节奏的软件开发环境中,追求高效、灵活的应用开发方式成为了开发团队的迫切需求。React低代码平台崭露头角,为开发人员提供了一种全新的开发范式,让开发过程更高效、更灵活,从而加速应用程序的开发周期和交付速度。 1. 快…...
多域名SSL证书:保护多个网站的安全之选
什么是多域名SSL证书? 多域名SSL证书,顾名思义,是指一张SSL证书可以保护多个域名。与传统的单域名SSL证书相比,多域名SSL证书可以在一个证书中绑定多个域名,无需为每个域名单独购买和安装SSL证书。这样不仅可以节省成…...
HarmonyOS—HAP唯一性校验逻辑
HAP是应用安装的基本单位,在DevEco Studio工程目录中,一个HAP对应一个Module。应用打包时,每个Module生成一个.hap文件。 应用如果包含多个Module,在应用市场上架时,会将多个.hap文件打包成一个.app文件(称…...

金三银四,程序员如何备战面试季
金三银四,程序员如何备战面试季 一个人简介二前言三面试技巧分享3.1 自我介绍 四技术问题回答4.1 团队协作经验展示 五职业规划建议5.1 短期目标5.2 中长期目标 六后记 一个人简介 🏘️🏘️个人主页:以山河作礼。 🎖️…...

VUE3项目学习系列--项目配置(二)
在项目团队开发过程中,多人协同开发为保证项目格式书写格式统一标准化,因此需要进行代码格式化校验,包括在代码编写过程中以及代码提交前进行自动格式化,因此需要进行在项目中进行相关的配置使之代码格式一致。 一、eslint配置 …...
idea:springboot项目搭建
目录 一、创建项目 1、File → New → Project 2、Spring Initializr → Next 3、填写信息 → Next 4、web → Spring Web → Next 5、填写信息 → Finish 6、处理配置不合理内容 7、注意事项 7.1 有依赖包,却显示找不到依赖,刷新一下maven 二…...

如何保证某个程序系统内只运行一个,保证原子性
GetMapping("/startETL") // Idempotent(expireTime 90, info "请勿90秒内连续点击")public R getGaugeTestData6() {log.info("start ETL");//redis设置t_data_load_record 值为2bladeRedis.set("t_data_load_record_type", 2);Str…...

golang常见面试题
1. go语言有哪些优点、特性? 语法简便,容易上手。 支持高并发,go有独特的协程概念,一般语言最小的执行单位是线程,go语言支持多开协程,协程是用户态线程,协程的占用内存更少,协程只…...

探索Python编程世界:从入门到精通
一.Python 从入门到精通 随着计算机科学的发展,编程已经成为了一种必备的技能。而 Python 作为一种简单易学、功能强大的编程语言,越来越受到人们的喜爱。本文将为初学者介绍 Python 编程的基础知识,帮助他们踏入 Python 编程的大门…...
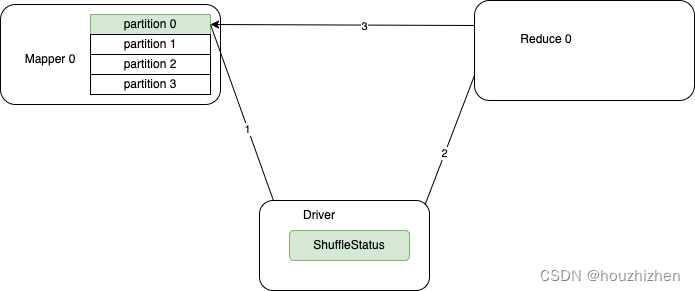
Spark Shuffle Tracking 原理分析
Shuffle Tracking Shuffle Tracking 是 Spark 在没有 ESS(External Shuffle Service)情况,并且开启 Dynamic Allocation 的重要功能。如在 K8S 上运行 spark 没有 ESS。本文档所有的前提都是基于以上条件的。 如果开启了 ESS,那么 Executor 计算完后&a…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...
