一命通关二分搜索

二分法
简介
和双指针一样,二分法也是一种优化方法,或者说二分法就是双指针的一类。不过,二分法的思想比双指针诞生更早也更广泛,在我们日常生活里也无时不刻在使用二分的思想。
比如我们想回顾某些影片,但是只记得影片的大概日期,我们往往会翻到最后一页,根据最后一页的日期再来取中估算出想找的影片可能对应的页数,通过不断重复来不断去定位影片的位置。

对于我们正常人来说,这种索引是灵活的,我们可以根据自己的需求来灵活调整二分的方法。
比如最后一页是100,我们在脑海里估算的时候,如果影片比较早,我们可能会定位到70页;如果影片是最近才出的,我们可能会定位到30页
但是,对于计算机,二分的算法是无法在程序进行的过程中调整的。也正因如此,二分会带来很多细节上的问题——死循环,越界等等,这也是二分最令人头疼的地方。但是二分作为一个将时间复杂度O(n)降为O(log n)的方法,在很多题中都作为了普遍的优化方法,所以单单研究出二分不是为了解决某种具体的问题,而是为将二分的思想运用到很多场景中。
朴素二分
朴素二分,就是我们在初学很多语言,第一次接触到的二分。
举一个很简单的例子704. 二分查找 - 力扣(LeetCode)

从一个有序数组中找到某个确定的值,最简单暴力的方法就是直接遍历,时间复杂度O(n)。但是从双指针的思想里,我们很容易发现,我们可以一边搜寻,一边排除。
比如我们想找到5这个元素,我们一开始便随便选一个元素下标,假设我们选择了元素9的下标。

找到9以后,将9和目标值比较,显然9是比5要大的。但是数组又是升序,我们就不需要考虑9以后的元素,只用在9前面的元素中再去找5。这样做的好处是什么?这样做显然将时间复杂度缩小了一半。
而我们不断重复这个过程,时间复杂度不断缩减为一半,最终时间复杂度就降为了O(log n)
同时,用某种方法可以证明,每次随便选择的数选择最中间的那个数,期望效率是最高的,具体证明方法就不解释了,因为我也不会。

简单用代码实现一下
int l=0;//左边界,从0开始
int r=nums.size()-1;//右边界,从最后一个元素开始while(l<=r)//循环条件:左边界在右边界左边
{int mid=l+(r-l)/2;//二分取中if(nums[mid]==target)//如果找到了,返回该下标return mid;else if(nums[mid]<target)//如果找到的数小于目标值,意味着mid和mid左边的值都不满足条件l=mid+1;//从mid右边继续寻找else//如果找到的数大于目标值,意味着mid和mid右边的值都不满足条件r=mid-1;//从mid左边继续寻找
}
//如果循环结束了,代表所有数都不满足条件,那么退出循环返回-1return -1;但是,既然叫他朴素二分,那自然意味着朴素二分只能解决一小部分问题。朴素二分太过老实了,只要问题场景一换,那么朴素二分就会出很多bug

把例子稍微换一下:

边界二分
此时发现,我们最朴素的二分已经不够用了。但是,是不是二分就完全用不上了呢?
在这里,纠正一个很多人最常见的误区:
二分不是只有数组顺序的时候才可以使用,
而是只要数组能满足区间规律,
就可以用二分来解决。
就比如在这里,虽然朴素二分用不上了,但是因为数组还是满足一个条件:
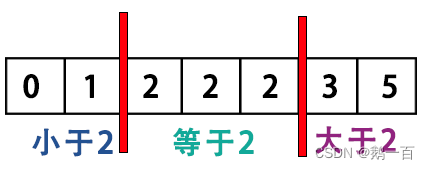
所以还是可以根据二分的思想,来找到每一个区间。
此时,我们想找到等于二的左区间,我们还是取二分中值的元素,发现等于2
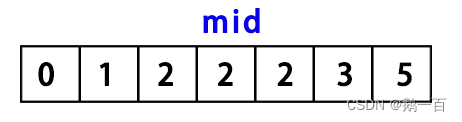
这也代表着,我们找到了等于2的区间中的一个元素,但是这却不一定是左边界,因为这个2可能会有三种情况:
- 为左边界
- 为中间的某个元素
- 为右边界
不过,无论是哪一种情况,都会对应一个结果:mid右边一定不存在我们想找的左边界,我们让right=mid,再来进行一次寻找。
但是,为什么right不能等于mid-1?因为mid可能就是左边界,如果right等于mid-1,那么就越过了左边界找不到结果。
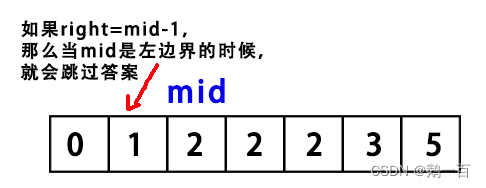
所以,我们可以轻易得到
再来看其他两种情况:
如果mid对应的元素小于target,那答案一定在mid的右边,也就是
如果mid对应的元素大于target,那答案一定在mid的左边,也就是
不过这里还有一个坑点:while循环的条件是什么?

我们来看这个情况:

所以,结束条件只能是:l<r
用代码实现一下:
int l=0;
int r=nums.size();while(l<r)
{int mid=l+(r-l)/2;if(nums[mid]<target)l=mid+1;elser=mid;//因为r=mid-1和r=mid效率几乎没有区别,所以合并成同一种情况
}return l;//出循环的时候一定是l==r,所以返回哪一个都无所谓右边界二分
再把问题变一下

此时上面的方法又行不通了,不过思考的方式还是一样的。
我们找到一个二分中值mid,可能有三种情况:
- nums[mid]==target,那右边界一定不在mid右边
- nums[mid]<target,那右边界一定在mid右边
- nums[mid]>target,那右边界一定在mid左边
总结下来还是那三种:
if(nums[mid]>target)r=mid-1;//如果mid对应的值大于,那么往左边找
elsel=mid;//和找左边界情况一样,为了避免跳过答案,所以一定不能为mid+1那是不是就这么简单解决了呢?当然不是,这又出现了一个新的坑点:

怎么解决这个问题?也很简单,mid=left+(right-left+1)/2就行了。
因为产生这个问题的根本原因,就是当left和right相邻的时候,mid应该是取left还是取right。我们直接从判断式来看
左边界是r=mid,但是为了避免死循环,r一定要产生改变,所以mid一定不能取r
右边界是l=mid,但是为了避免死循环,l一定要产生改变,所以mid一定不能取l
所以在这里,我们的mid一定要取right对应的值,而这个问题说人话就是,向下取整和向上取整的问题。
用代码实现一下:
int l=0;
int r=nums.size();while(l<r)
{int mid=l+(r-l+1)/2;//向上取整if(nums[mid]>target)r=mid-1;elsel=mid;
}return l;//出循环的时候一定是l==r,所以返回哪一个都无所谓边界总结和模板
说了这么多,左边界和右边界其实有着很大的共性:
- 循环条件一定是l<r
- 出循环的时候,最终都会为l==r,无论返回哪一个都一样
但是,我们怎么判断左边界和右边界的区别?什么时候用什么代码?
其实只需要考虑两个问题:
1.是大于等于还是大于
我们来看一下右边界情况的语言描述:

不在右边,也就是>=,代表着包含着当前的元素,也就对应着l=mid
在右边和在左边,也就是>和<,代表着不包含当前的元素,也就对应着l=mid+1和r=mid-1
而说白了,也就是个最简单的数学表达式描述问题,我们只需要看着文字,然后转换成数学式,小学生都会。
2.向上还是向下取整来避免死循环
在右边界二分的时候,就已经详细说明了,我们取mid的不同其实就是为了避免进入死循环,而解决方法就是通过判断是l=mid还是r=mid,来分别向上取整和向下取整。

所以,最终可以总结出求左右边界的模板:
int l=0;
int r=nums.size();while(l<r)
{1.判断mid是向上取整还是向下取整2.列出三种情况,然后分别转化成两个数学判断表达式
}return l;所有二分问题都可以通过这个模板来解决。
而看完了这些,再去尝试这道题,只有自己亲自动手理解和解出来,才表示完全掌握了二分模板。
34. 在排序数组中查找元素的第一个和最后一个位置 - 力扣(LeetCode)![]() https://leetcode.cn/problems/find-first-and-last-position-of-element-in-sorted-array/description/
https://leetcode.cn/problems/find-first-and-last-position-of-element-in-sorted-array/description/

相关文章:

一命通关二分搜索
二分法 简介 和双指针一样,二分法也是一种优化方法,或者说二分法就是双指针的一类。不过,二分法的思想比双指针诞生更早也更广泛,在我们日常生活里也无时不刻在使用二分的思想。 比如我们想回顾某些影片,但是只记得…...

串联所有单词的子串
题目链接 串联所有单词的子串 题目描述 注意点 words[i] 和 s 由小写英文字母组成1 < words.length < 5000可以以 任意顺序 返回答案words中所有字符串长度相同 解答思路 根据滑动窗口哈希表解决本题,哈希表存储words中所有的单词及单词的出现次数&#…...

【会议征稿通知】第四届经济发展与商业文化国际学术会议(ICEDBC2024)
第四届经济发展与商业文化国际学术会议(ICEDBC2024) The 4th International Conference on Economic Development and Business Culture (ICEDBC 2024) 第四届经济发展与商业文化国际学术会议(ICEDBC2024)将于2024年6月21-23日在…...
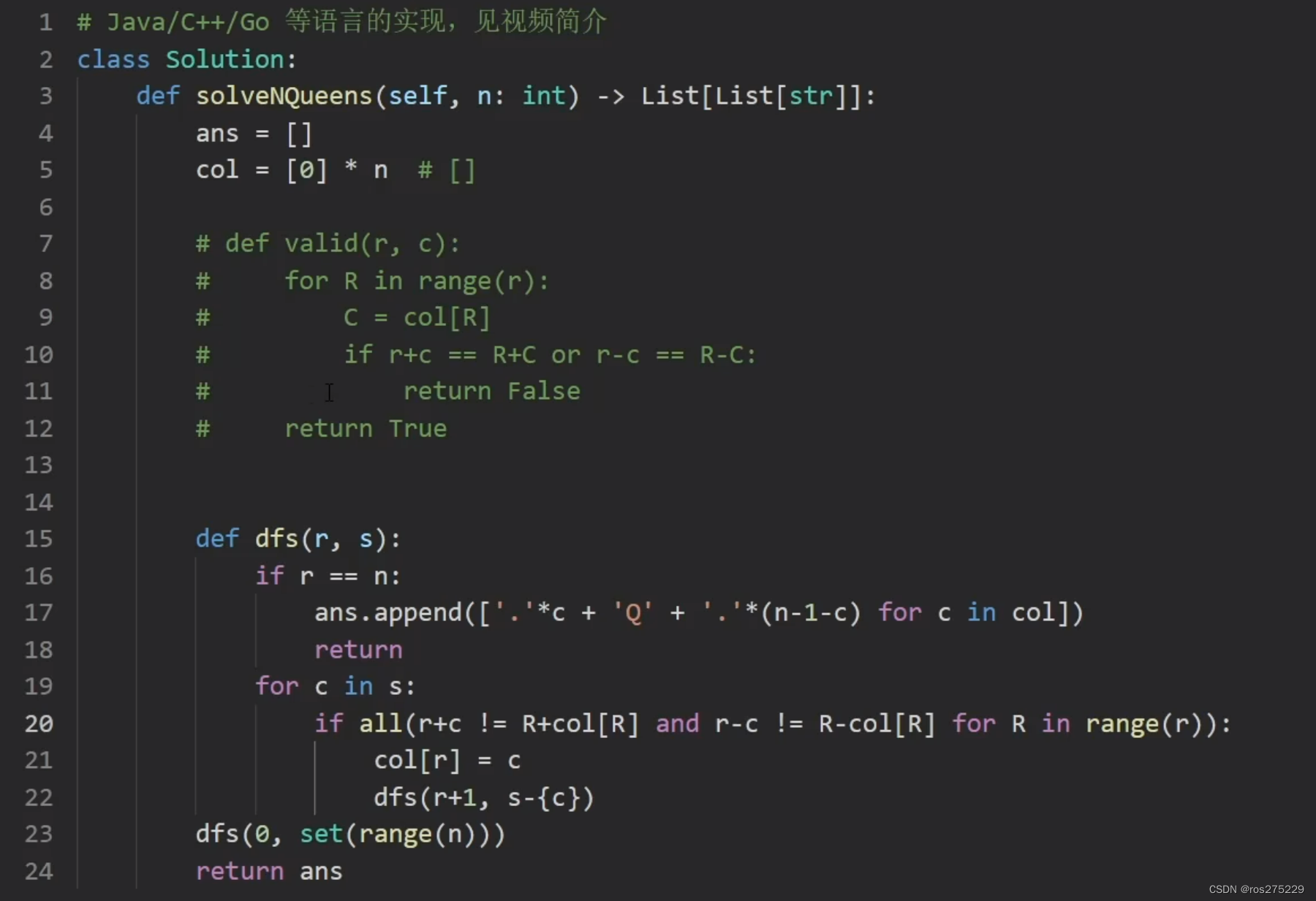
回溯算法套路③排列型回溯+N皇后【基础算法精讲 16】
46 . 全排列 链接 : . - 力扣(LeetCode) 思路 : 那么怎么确定选了那个数呢? 这里设置一个used表示i选没选过 ; class Solution { public:vector<vector<int>> ans;vector<int> path;void backtrack(vector<int>nums,vect…...

MyBatis-Plus 框架中的自定义元对象处理器
目录 一、代码展示二、代码解读 一、代码展示 package com.minster.yanapi.handler;import com.baomidou.mybatisplus.core.handlers.MetaObjectHandler; import org.apache.ibatis.reflection.MetaObject; import org.springframework.stereotype.Component;import java.util…...
)
Node.js_基础知识(fs模块 - 文件操作)
写入 文件操作 流式写入:fs.createWriteStream(path[, options]) 可以减少打开关闭文件的次数适用于:大文件写入、频繁写入参数说明: path:文件路径文件夹操作: 调用mkdir方法:fs.mkdir(./a/b/c, err => {}) 递归创建文件夹:加参数recursive fs.mkdir(./a/b/c, {recu…...

基于C#开发OPC DA客户端——搭建KEPServerEX服务
简介 OPC DA (OLE for Process Control Data Access) 是一种工业自动化领域中的通信协议标准,它定义了应用程序如何访问由OPC服务器提供的过程控制数据。OPC DA标准允许软件应用程序(客户端)从OPC服务器读取实时数据或向服务器写入数据&…...
)
让你的函数,返回你需要的“两个值” (函数传址、结构体作为参数传参)
总结:1.结构体完成你的目标 2.指针传参 方法2. void get_a_b(int* a, int* b) { *a 13; *b 14; //通过解引用,找到并修改 } int main() { int a 0; int b 0; get_a_b(&a, &b); //传地址 prin…...

快速上手:在 Android 设备上运行 Pipy
Pipy 作为一个高性能、低资源消耗的可编程代理,通过支持多种计算架构和操作系统,Pipy 确保了它的通用性和灵活性,能够适应不同的部署环境,包括但不限于云环境、边缘计算以及物联网场景。它能够在 X86、ARM64、海光、龙芯、RISC-V …...

【操作系统学习笔记】文件管理1.3
【操作系统学习笔记】文件管理1.3 参考书籍: 王道考研 视频地址: Bilibili I/O 控制方式 程序直接控制方式中断驱动方式DMA 方式通道控制方式 程序直接控制方式 关键词: 轮询 完成一次读/写操作的流程 CPU 向控制器发出读指令。于是设备启动,并且状态寄存器设…...
基于springboot+vue的酒店管理系统
博主主页:猫头鹰源码 博主简介:Java领域优质创作者、CSDN博客专家、阿里云专家博主、公司架构师、全网粉丝5万、专注Java技术领域和毕业设计项目实战,欢迎高校老师\讲师\同行交流合作 主要内容:毕业设计(Javaweb项目|小程序|Pyt…...

Linux 相关命令
文章目录 目录相关操作vim 编辑器命令行模式插入模式底行模式 目录相关操作 查看当前目录下的文件 ls创建目录 mkdir 目录名进入文件,首先确认位于文件的目录 vi 文件名 vim 编辑器 命令行模式 控制光标的移动,字符或行的删除,移动复制某区域…...
阿里云搭建私有docker仓库(学习)
搭建私有云仓库 首先登录后直接在页面搜索栏中搜索“容器镜像服务” 进入后直接选择个人版(可以免费使用) 选择镜像仓库后创建一个镜像仓库 在创建仓库之前我们先创建一个命名空间 然后可以再创建我们的仓库,可以与我们的github账号进行关联…...
)
MySQL数据库基本操作(一)
数据库的基本概念 1. 数据库的英文单词: DataBase 简称 : DB 2. 什么数据库?* 用于存储和管理数据的仓库。 3. 数据库的特点:1. 持久化存储数据的。其实数据库就是一个文件系统2. 方便存储和管理数据3. 使用了统一的方式操作数…...

【暗月安全】2021年渗透测试全套培训视频
参与培训需要遵守国家法律法规,相关知识只做技术研究,请勿用于违法用途,造成任何后果自负与本人无关。 中华人民共和国网络安全法(2017 年 6 月 1 日起施行) 第二十二条 任何个人和组织不得从事入侵他人网络、干扰他…...

HTML极速入门
HTML基础 什么是HTML HTML(Hyper Text Markup Language),超文本标记语言. 超文本:比文本更强大.通过链接和交互式方式来组织和呈现信息的文本形式.不仅仅有文本,还可能包括图片,音频,或者自己经审阅过它的学者所加的评注,补充或脚注等. 标记语言:由标签构成的语言 HTML的标…...
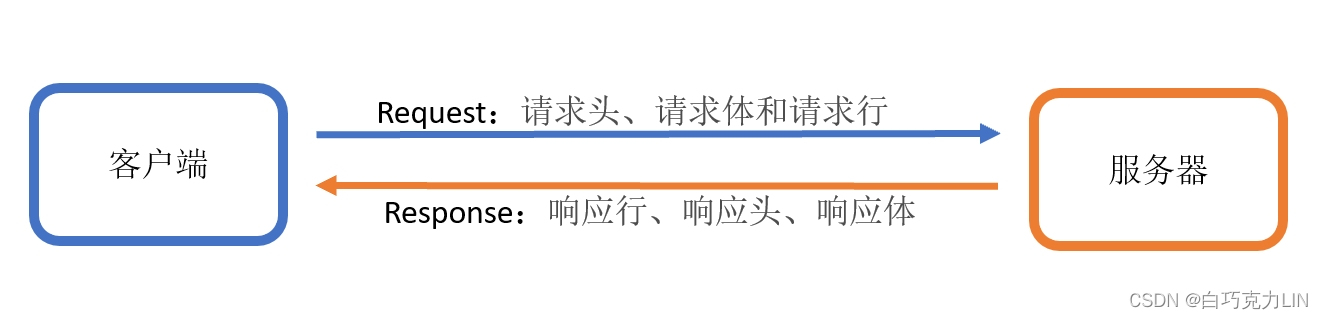
Django框架——请求与响应
上篇文章我们学习了Django框架——配置文件和视图函数,这篇文章我们学习Django框架——请求与响应。 客户端和服务端的请求与响应过程:客户端访问某个网站并发出URL请求,服务器接受到请求后,根据请求内容来返回响应,如…...
)
rearrangement-challenge-2022环境使用学习(一)
搭建了rearrangement-challenge-2022的环境: https://github.com/facebookresearch/habitat-challenge/tree/rearrangement-challenge-2022 habitat最大的缺点是对不同的版本非常的敏感。本文只是针对rearrangement-challenge-2022的学习。 文档一开始会很不完善&a…...
)
[Uniapp]携带参数跳转界面(两种方法)
一、方法1:路由携参 假设现在有两个界面:界面A和界面B。并要由界面A跳转到界面B,则我们可以使用 uni.navigateTo({}) 跳转界面时,将参数附加在URL后,…...
:python常用网络请求库httpx)
Scrapy与分布式开发(2.1.2):python常用网络请求库httpx
Python httpx 模块详细讲解 一、引言 httpx 是一个用于发送 HTTP 请求的 Python 库,它提供了简单易用的 API,支持同步和异步请求,并且具有出色的性能和灵活性。httpx 是 requests 的一个现代替代品,它使用 httpcore 作为底层传输…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...

