运筹学_1.1.4 线性规划问题-解的概念
1.1.4 线性规划问题-解的概念
- 一、可行解与最优解
- 二、基的概念
- 三、基变量、基向量;非基变量、非基向量;基解、基可行解;
- 四、最优解与可行解、基可行解的关系
- 五、用例题(枚举法)巩固基解、基可行解、最优解三个概念
- 1、例1
- 2、例2
- 六、解之间的关系归纳
一、可行解与最优解

可行解:满足所由约束条件的解【全部可行解的集合称为可行域】
最优解:使目标函数最大的可行解
因此最优解包含于可行解
二、基的概念
基:设A是约束方程组(2)的m×n阶系数矩阵(设n>m,变量的个数大于方程的个数),
其秩为m。
B是A中的一个m×m阶的满秩子矩阵(|B|≠0的非奇异子矩阵),则称B为线性规划问题的一个基。
B实际上就是A的一个极大线性无关组
问题1:为什么秩就为m?
实际过程中,在建模时列约束条件,默认列出来的方程为独立方程(而不会出现两个方程化简后相同的无效方程情况)问题2:为什么n>m?
实际情况中,决策变量的个数通常也是大于方程的个数

三、基变量、基向量;非基变量、非基向量;基解、基可行解;
设方程组有m个方程,n个变量,其中n>m.R(A)=m,方程组有n-m个自由未知量,即方程组一定有无穷多个解。
n=m时只有唯一解,实际情况很少出现。

假设:方程组中前m个变量的系数列向量就是它的基向量(极大线性无关组)
则把(n-m)个非基向量移项到右边

非基变量可以是任意常数,因此令所有非基变量为0,又因为|B|≠0,据克莱姆法则,可求出唯一解;
从而得到第一个初始解XB
则X=(XB,XN)


因此,在约束方程组中的系数矩阵中找到一个基,就能求出一组基解

基解不一定是可行解
基解:根据基求得的解
基可行解:基解中所有分量都满足非负条件的解
可行基:对应于基可行解的基
四、最优解与可行解、基可行解的关系
最优解一定在可行解当中,那最优解一定包含在基可行解中吗?
1、当最优解唯一时,最优解也是基最优解;
2、当最优解不唯一时,最优解不一定是基最优解

五、用例题(枚举法)巩固基解、基可行解、最优解三个概念
基的数目为:C(m,n)- 行列式为0的矩阵数,
基可行解为:分量都为非负的基解
1、例1



2、例2

六、解之间的关系归纳
可以用图解法辅助理解

相关文章:

运筹学_1.1.4 线性规划问题-解的概念
1.1.4 线性规划问题-解的概念 一、可行解与最优解二、基的概念三、基变量、基向量;非基变量、非基向量;基解、基可行解;四、最优解与可行解、基可行解的关系五、用例题(枚举法)巩固基解、基可行解、最优解三个概念1、例…...

物联网主机:为智能交通赋能
物联网(IoT)技术的发展为智能交通领域带来了许多创新的解决方案。而在物联网应用中,物联网主机起着关键的作用。本文将为大家介绍一款名为E6000的物联网主机,它是一种多协议、多接口的物联网主机,为智能交通系统的建设…...

「Vue3系列」Vue3简介及安装
文章目录 一、Vue3简介二、Vue3安装三、Vue3应用案例四、package.json详解五、相关链接 一、Vue3简介 Vue3是Vue.js框架的第三个主要版本,于2020年9月18日发布,代号为“One Piece”。Vue3在性能、体积、TypeScript支持、API设计等方面都有显著的提升和改…...

Javascript:分支语句
一、前言 关于分支语句的介绍来啦,开始记笔记。 二、正文 1.分支语句if 分支语句就是通过判断已给的表达式的条件来执行语句,表达式为真才能执行. if(条件){满足条件才要执行的代码} 条件为true时,才能进行大括号的代码。 除了空字符串&am…...
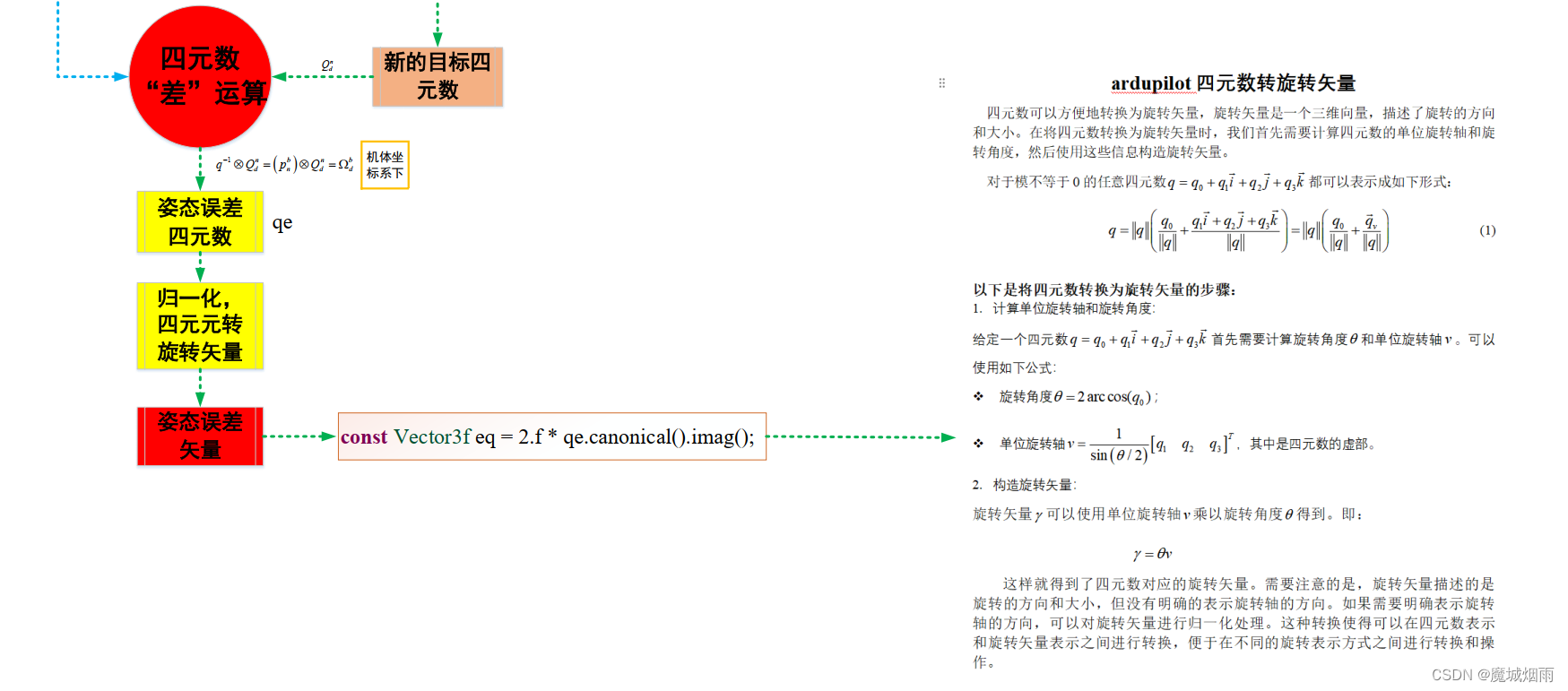
从零开始学习PX4源码2(PX4姿态误差计算)
目录 文章目录 目录摘要1.源码1.1源码路径1.2源码程序1.3源码功能 2.源码分析 摘要 本节主要记录PX4姿态误差计算过程,欢迎批评指正。 1.源码 1.1源码路径 PX4-Autopilot/src/modules/mc_att_control/AttitudeControl/AttitudeControl.cpp1.2源码程序 matrix::…...
git安装与使用4.3
一、git的安装 1、下载git包 下载git包url:https://git-scm.com/download/win 下载包分为:64位和32位 2、点击安装包 2、选择安装路径 3、 点击下一步 4、点击next 5、点击next 6、点击next 7、 8、 9、 10、 11、 12、在桌面空白处,右键…...
Python:关于数据服务中的Web API的设计
搭建类似joinquant、tushare类似的私有数据服务应用,有以下一些点需要注意: 需要说明的是,这里讨论的是web api前后端,当然还有其它方案,thrift,grpc等。因为要考虑到一鱼两吃,本文只探讨web ap…...
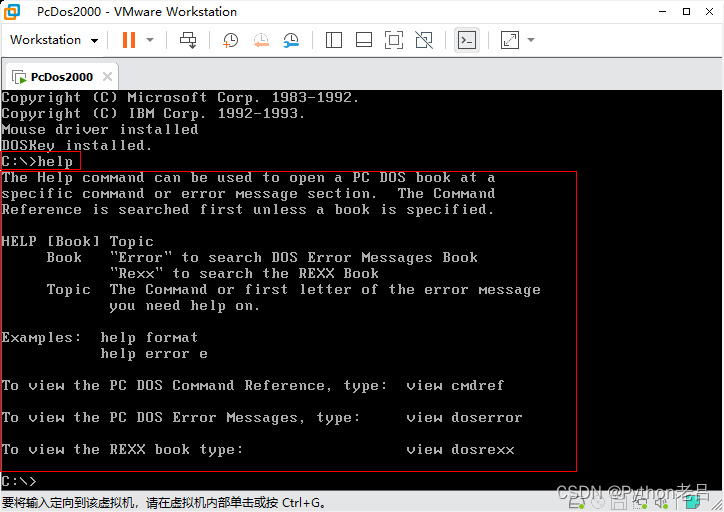
VMwareWorkstation17.0虚拟机安装搭建PcDos2000虚拟机(完整图文详细步骤教程)
VMwareWorkstation17.0虚拟机安装搭建PcDos2000虚拟机(完整图文详细步骤教程) 一、PcDos20001.PcDos2000简介2.PcDos2000下载 二、创建PcDos2000虚拟机1.新建虚拟机2.类型配置3.类型配置4.选择版本5.命名、存位置6.磁盘容量7.调整虚拟配置7.1 调整虚拟配…...
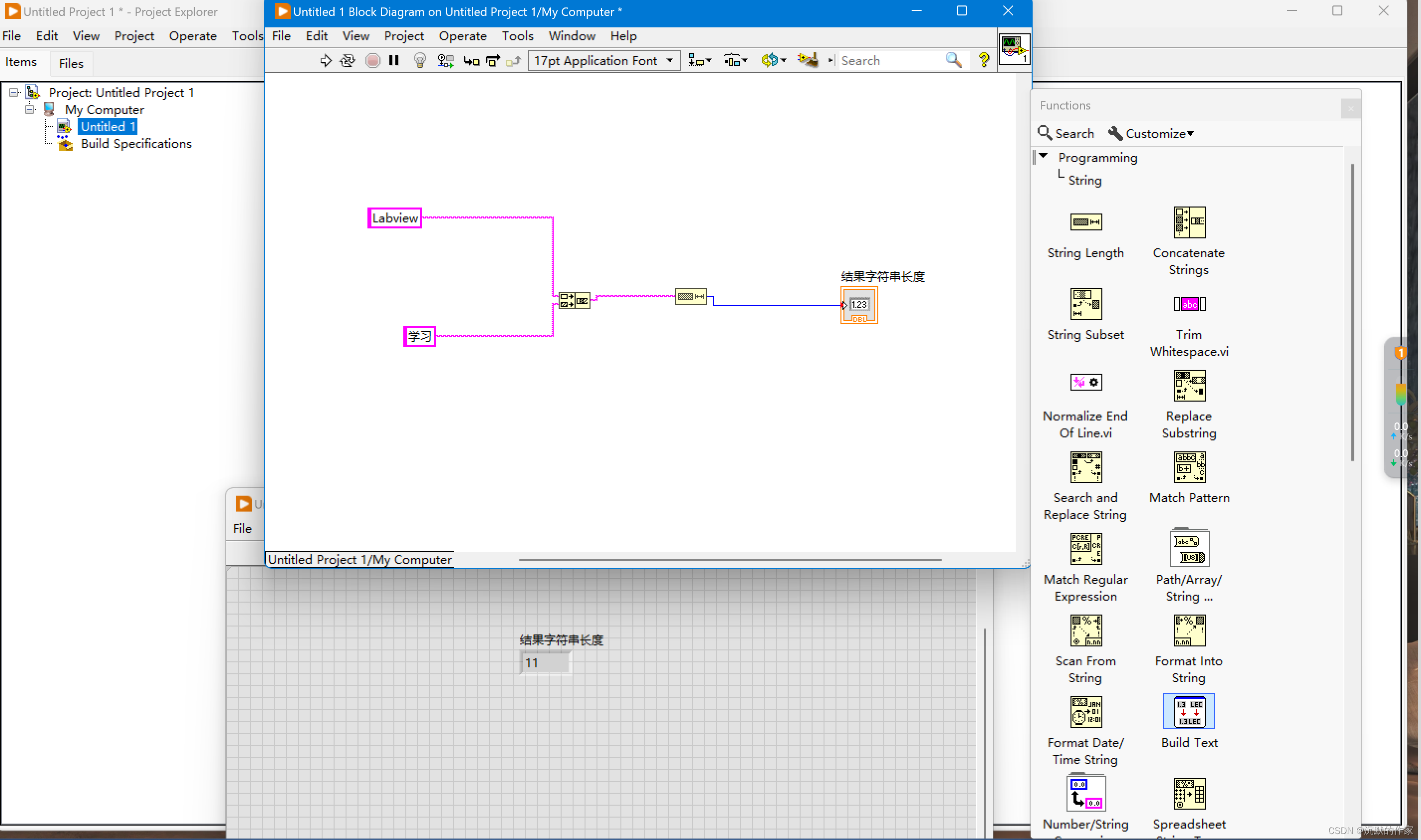
第七个程序:两个字符串连接后计算长度
实验步骤; 第一步:新建项目 第二步:程序编写 第三步:运行结果 Labview一共7个字节,长度为7,一个字母一个字节 汉字为2个字节,图一为4,图二为8 所以结果分别为11和15 视频教学: 字…...

【大数据】-- dataworks 创建odps 的 hudi 外表
文档:创建OSS外部表_云原生大数据计算服务 MaxCompute(MaxCompute)-阿里云帮助中心 举例:创建 odps 的 hudi 外表 CREATE EXTERNAL TABLE IF NOT EXISTS my_project.ods_hudi_mysql_words_h_all (id BIGINT COMMENT 主键id,`words` STRING COMMENT 词…...

ChatGPT与GEE+ENVI+python高光谱,多光谱等成像遥感数据处理技术
原文链接:ChatGPT与GEEENVIpython高光谱,多光谱等成像遥感技术 第一遥感科学与AI基础 一:遥感科学的基本原理和历史 从摄影侦察到卫星图像 遥感的基本原理 遥感的典型应用 最新进展和未来趋势 二:ChatGPT 什么是ChatGPT&a…...

学习linux从0到初级工程师-3
一、LNMP 1.1 搭建LNMP LNMP:LinuxNginxMysqlPHP LNMP优势: 1.web服务器一种,Nginx处理静态文件、索引文件,自动索引的效率非常高; 2.作为代理服务器,Nginx可以实现无缓存的反向代理加速,提高网站运行…...
java实现文件上传到本地
很多时候我们都需要进行文件上传和下载的操作,具体怎么实现网上的代码其实也是挺多的,刚好我的项目中也遇到了文件上传和下载的需求,本篇博文具体讲解上传操作,下篇博文讲解下载操作。 我们具体来想一想要将一个从前端传来的文件…...
基于springboot+vue的多媒体素材库的开发与应用系统
博主主页:猫头鹰源码 博主简介:Java领域优质创作者、CSDN博客专家、阿里云专家博主、公司架构师、全网粉丝5万、专注Java技术领域和毕业设计项目实战,欢迎高校老师\讲师\同行交流合作 主要内容:毕业设计(Javaweb项目|小程序|Pyt…...
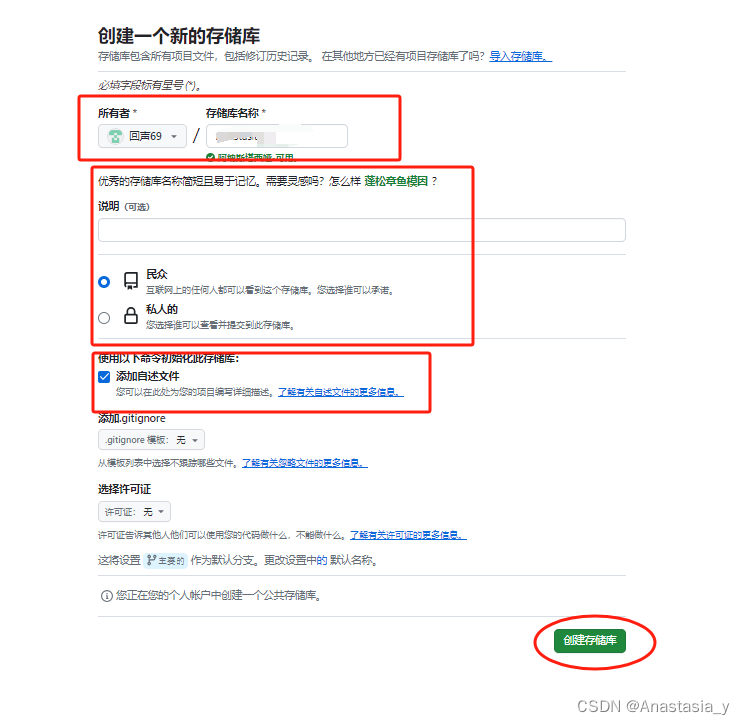
《GitHub新手入门指南:从零开始掌握基本用法》
在现代软件开发和技术社区中,GitHub已经成为了一个不可或缺的平台。它不仅是一个代码托管平台,更是一个技术交流、学习分享的社交平台。但对于初学者来说,GitHub可能会有些令人望而却步。本文将详细介绍GitHub的基本用法,帮助新手快速入门并融入这个充满活力的技术社区。 …...

K8S存储卷与PV,PVC
一、前言 Kubernetes(K8s)中的存储卷是用于在容器之间共享数据的一种机制。存储卷可以在多个Pod之间共享数据,并且可以保持数据的持久性,即使Pod被重新调度或者删除,数据也不会丢失。 Kubernetes支持多种类型的存储卷…...
简答题汇总)
(科目三)简答题汇总
模块一 信息和计算机基础 一、简述信息的的特征 【记忆技巧】普传功夫真驾驶 普遍性:信息是无时不有的,无时不在的载体依附性:信息不能独立存在,必须有载体。价值性:同一则信息,对不同的人来说,价值不同。时效性:同…...

8、Redis-Jedis、Lettuce和一个Demo
目录 一、Jedis 二、Lettuce 三、一个Demo Java集成Redis主要有3个方案:Jedis、Lettuce和Redisson。 其中,Jedis、Lettuce侧重于单例Redis,而Redisson侧重于分布式服务。 项目资源在文末 一、Jedis 1、创建SpringBoot项目 2、引入依赖 …...
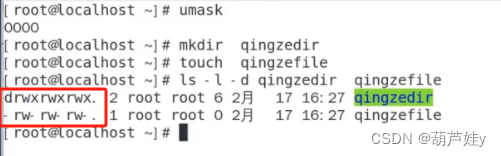
(Linux学习六)用户特殊权限类型,suid,chattr,umask
一、特殊位suid,针对文件/程序时,具备临时提升权限 分析:root运行是超管的权限,普通用户运行时是普通用户的权限 root /usr/bin/cat(root) /root/file1.txt ok alice/usr/bin/cat(alice) /root/file1.txt 无法访问rootchmod us filename …...
)
Mysql 数据类型的转换之 cast()
语法 cast( value as type) value 要进行数据转换的值(可以为任何类型)。type 要转换为的数据类型。type 的常见的类型可以为 : decimal十进制浮点数。可以使用可选的 M 和 D 参数指定最大位数 (M) 和小数点后的位数 (D)float浮点数dou…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...

微服务通信安全:深入解析mTLS的原理与实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、引言:微服务时代的通信安全挑战 随着云原生和微服务架构的普及,服务间的通信安全成为系统设计的核心议题。传统的单体架构中&…...
