(MATLAB)第十二章-数列与极限
目录
12.1 数列
12.1.1 数列求和
1. 累计求和函数sum()
2. 忽略NaN累计求和函数 nansum()
3. 求此元素位置之前的元素和函数cumsum()
4. 求梯形累计和函数cumtrapz()
12.1.2 数列求积
1. 元素连续相乘函数 prod()
2. 求累计积函数 cumprod()
3. 阶乘函数 f=factorial(n) n!,n为非负整数值
4. 伽马函数 gamma()
12.2 极限和导数
12.2.1 极限
12.2.2 导数
12.3 级数求和
12.3.1 有限项级数求和
12.3.2 无穷级数求和
参考资料:
12.1 数列
12.1.1 数列求和
1. 累计求和函数sum()
| 调用格式 | 说明 |
| S=sum(A) | (1)A为向量,返回所有元素和,结果是一个数值; (2)A为矩阵,返回每一列所有元素和,结果为数值个数等于列数的行向量; (3)A为n维阵列,相当于n个矩阵,则返回n个矩阵累和(按列) |
| S=sum(A,dim) | (1)对于向量求和运算:dim=1,不求和,返回原数列;dim=2,求和; (2)对于矩阵求和运算:dim=1,对列求和,结果组成行向量;dim=2,对行求和,结果则称列向量 |
| S=sum(A,vecdim) | 根据向量vecdim中指定的维度对A的元素进行求和 |
| S=sum(A,’all’) | 计算A的所有元素的值,包括行列与维度的和,结果是单个数值 |
| S=sum(…,outtype) | 可以设置特殊格式的累计和值,输出类型outtype包含’defalult’、’double’、’native’ |
| S=sum(…,nanflag) | 若向量或矩阵中包含NaN,在此格式下nanflag可以设置是否计算NaN,nanflag参数设置为’includenan’表示计算,设置为’omitnan’表示忽略 |
2. 忽略NaN累计求和函数 nansum()
| 调用格式 | 说明 |
| S=nansum(A) | 累计和中不包括NaN |
| … | … |
nansum(A)与sum(A,omitnan)可以通用,前者步骤更简洁
3. 求此元素位置之前的元素和函数cumsum()
函数cumsum()求解的是新定义的累计和,即每个位置的新元素值不包括当前项的元素之和。
略,详见MA1.269-270
4. 求梯形累计和函数cumtrapz()
略,详见MA1.270-273
12.1.2 数列求积
1. 元素连续相乘函数 prod()
| 调用格式 | 说明 |
| B=prod(A) | (1)A为向量,返回所有元素和,结果是一个数值; (2)A为矩阵,返回每一列所有元素积,结果为数值个数等于列数的行向量; |
| B=prod(A,dim) | (1)对于向量求和运算:dim=1,不求积,返回原数列;dim=2,求积; (2)对于矩阵求和运算:dim=1,对列求积,结果组成行向量;dim=2,对行求积,结果则称列向量 |
| B=prod(A,vecdim) | 根据向量vecdim中指定的维度对A的元素进行求积,其中不包括NaN |
| B=prod(A,’all’) | 计算A的所有元素的乘积 |
| B=prod(…, type) | 可以设置特殊格式的累计和值,输出类型outtype包含’defalult’、’double’、’native’ |
2. 求累计积函数 cumprod()
略,详见MA1.274
3. 阶乘函数 f=factorial(n) n!,n为非负整数值
4. 伽马函数 gamma()
伽马函数(Gamma Function)也叫欧拉第二积分,是阶乘函数在实数与复数上扩展的一类函数,一般情况下,阶乘是定义在正整数和0(大于等于0)的范围里的,小数没有阶乘,这里将函数gamma()定义为非整数的阶乘,作为阶乘的延拓,是定义在复数范围内的亚纯函数,通常写作Γ(x)
在实数域上伽马函数定义为
在复数域上伽马函数定义为
同时,gamma()也适用于正整数,factorial()同用法
补充:不完全伽马函数gammainc(),其中
12.2 极限和导数
在工程计算中,经常会研究某一函数随自变量的变化趋势与相应的变化率,也就是要研究函数的极限和导数问题。
12.2.1 极限
极限是数学分析最基本的概念和出发点,在工程实际中,其计算往往比较繁琐。在MATLAB中,运用limit命令可以解决。调用格式:
| 调用格式 | 说明 |
| limit(f,x,a) 或 limit(f,a) | 求解 |
| limit(f) | 求解 |
| limit(f,x,a,’right’) | 求解 |
| limit(f,x,a,’left’) | 求解 |
示例1:
>> clear
>> syms x;
>> f=sin(x)/x;
>> limit(f)
ans =1示例2:
>> syms n
>> limit((1+1/n)^n,inf)
ans =exp(1)
示例3:
>> syms x
>> limit(log(1+x)/x,x,0,'right')
ans = 1
示例4:计算,注意此处是二元函数的极限
>> syms x y %定义符号变量x y
>> f=(exp(x)+exp(y))/(cos(x)-sin(y)); %定义符号表达式
>> limit(limit(f,x,0),y,0) %先求x趋近于0时的符号表达式f的极限值,再求y趋近于0的极限值
ans =212.2.2 导数
导数是数学分析的基础内容之一,在工程运用中用来描述各种各样的变化率。可以根据导数的定义,利用limit命令求解,同时MATLAB也提供了专门的函数求导命令diff。调用格式:
| 调用格式 | 说明 |
| Y=diff(X) | 计算沿大小不等于1的第一个数组维度的X相邻元素之间的差分 |
| Y=diff(X,n) | 通过递归应用diff(X)运算n次求n阶导数 |
| Y=diff(X,n,dim) | 求沿dim指定的维度计算的第n个差分 |
示例1:
>> clear
>> syms x
>> f=2^x+x^(1/2)*log(x);
>> diff(f) %求表达式f的一阶导数
ans = log(x)/(2*x^(1/2)) + 2^x*log(2) + 1/x^(1/2)
示例2:
>> syms x
>> f=(1-cos(x))/(3*x^2);
>> diff(f,1) %求表达式f的一阶导数
ans = sin(x)/(3*x^2) + (2*(cos(x) - 1))/(3*x^3)
>> diff(f,2) %求表达式f的二阶导数
ans = cos(x)/(3*x^2) - (4*sin(x))/(3*x^3) - (2*(cos(x) - 1))/x^4>> diff(f,3) %求表达式f的三阶导数
ans = (6*sin(x))/x^4 - sin(x)/(3*x^2) - (2*cos(x))/x^3 + (8*(cos(x) - 1))/x^5
示例3:
>> syms x
>> limit(log(1+x)/x,x,0,'right')
ans = 1
示例4: 计算对x、y的1阶、2阶偏导数
>>clear
>>syms x y %定义符号变量x y
>>f=log(exp(2*(x+y^2))+(x^2+y)+sin(1+x^2)); %定义符号表达式
>>fx=diff(f,x) %计算f对x的1阶导数
fx =(2*x + 2*exp(2*y^2 + 2*x) + 2*x*cos(x^2 + 1))/(y + sin(x^2 + 1) + exp(2*y^2 + 2*x) + x^2)
>>fy=diff(f,y) %计算f对y的一阶导数
fy =(4*y*exp(2*y^2 + 2*x) + 1)/(y + sin(x^2 + 1) + exp(2*y^2 + 2*x) + x^2)
>>fxy=diff(fx,y) %对x求导后,再对y求导
fxy =(8*y*exp(2*y^2 + 2*x))/(y + sin(x^2 + 1) + exp(2*y^2 + 2*x) + x^2) - ((4*y*exp(2*y^2 + 2*x) + 1)*(2*x + 2*exp(2*y^2 + 2*x) + 2*x*cos(x^2 + 1)))/(y + sin(x^2 + 1) + exp(2*y^2 + 2*x) + x^2)^2
>>fyx=diff(fy,x) %对y求导后,再对x求导
fyx =(8*y*exp(2*y^2 + 2*x))/(y + sin(x^2 + 1) + exp(2*y^2 + 2*x) + x^2) - ((4*y*exp(2*y^2 + 2*x) + 1)*(2*x + 2*exp(2*y^2 + 2*x) + 2*x*cos(x^2 + 1)))/(y + sin(x^2 + 1) + exp(2*y^2 + 2*x) + x^2)^2
>>fxx=diff(fx,x) %再次对x求导(等价于求二阶导)
fxx =(2*cos(x^2 + 1) + 4*exp(2*y^2 + 2*x) - 4*x^2*sin(x^2 + 1) + 2)/(y + sin(x^2 + 1) + exp(2*y^2 + 2*x) + x^2) - (2*x + 2*exp(2*y^2 + 2*x) + 2*x*cos(x^2 + 1))^2/(y + sin(x^2 + 1) + exp(2*y^2 + 2*x) + x^2)^2
>>fyy=diff(fy,y) %再次对y求导(等价于求二阶导)
fyy =(4*exp(2*y^2 + 2*x) + 16*y^2*exp(2*y^2 + 2*x))/(y + sin(x^2 + 1) + exp(2*y^2 + 2*x) + x^2) - (4*y*exp(2*y^2 + 2*x) + 1)^2/(y + sin(x^2 + 1) + exp(2*y^2 + 2*x) + x^2)^2
>>fxx=diff(f,x,2) %略
>>fyy=diff(f,y,2) %略
12.3 级数求和
级数是数学分析的重要内容,无论对于数学理论本身还是在科学技术的应用中都是一个有力的工具。
12.3.1 有限项级数求和
求级数命令symsum,调用格式:
| 调用格式 | 说明 |
| F=symsum(f,k) | 返回级数f关于指数k的有限项和 |
| F=symsum(f,k,a,b) | 返回级数f关于指数从a到b的有限项和 |
示例1:
>> syms a b n %定义符号变量
>> s=a^n+b*n; %定义符号表达式
>> symsyn(s,n,0,n) %计算级数关于指数n从0到n共n+1项的有限项和
ans =piecewise(a == 1, n + (b*n)/2 + (b*n^2)/2 + 1, a ~= 1, -(b*n + b*n^2 - 2*a*a^n - a*b*n - a*b*n^2 + 2)/(2*(a - 1)))
示例2:
>> syms n x
>> s=sin(n*x);
>> symsum(s,n,0,n)
ans =piecewise(in(x/(2*pi), 'integer'), 0, ~in(x/(2*pi), 'integer'), (exp(-x*(n + 1)*1i)*(exp(x*(n + 1)*1i) - exp(x*(n + 1)*2i) - exp(x*1i) + exp(x*(n + 1)*1i)*exp(x*1i))*1i)/(2*(exp(x*1i) - 1)))
示例3:计算级数的前n+1项(n从0开始),并求前11项的和
>>syms n
>>s=2*sin(2*n)+4*cos(4*n)+2^n;
>>sum_n=symsum(s)
sum_n =(exp(-2i)^n*1i)/(exp(-2i) - 1) - (exp(2i)^n*1i)/(exp(2i) - 1) + (2*exp(-4i)^n)/(exp(-4i) - 1) + (2*exp(4i)^n)/(exp(4i) - 1) + 2^n
>>sum10=symsum(s,0,10)
sum10 =4*cos(4) + 4*cos(8) + 4*cos(12) + 4*cos(16) + 4*cos(20) + 4*cos(24) + 4*cos(28) + 4*cos(32) + 4*cos(36) + 4*cos(40) + 2*sin(2) + 2*sin(4) + 2*sin(6) + 2*sin(8) + 2*sin(10) + 2*sin(12) + 2*sin(14) + 2*sin(16) + 2*sin(18) + 2*sin(20) + 2051
>> vpa(sum10) %控制级数前1项和的精度ans =2048.2771219312785147716264587939
注:若不知道级数s中的变量是哪个,采用symvar命令:C=symvar(expr),搜索表达式expr,查找除i、j、pi、inf、nan、eps和公共函数之外的标识符。这些标识符是表达式中变量的名称。
12.3.2 无穷级数求和
MATLAB中的symsum命令该可以求无穷级数,此时只需将命令参数中的求和区间改为无穷即可。示例如下:
>> syms n
>> s1=1/n;
>> v1=symsum(s1,n,1,inf) %计算级数s1关于指数n从1到+∞的和
v1 =Inf 实际上,该级数发散>> s2=1/n^3;
>> v2=symsum(s2,n,1,inf)
v2 =zeta(3)
>> vpa(v2) %控制v2的精度
ans =1.2020569031595942853997381615114
zeta(3)表示zeta函数在3处的值,其中函数zeta()的定义是
MATLAB并不是可以计算出所有的级数求和结果,求不出时答案会给出求和形式:
计算级数
>> syms n
>> s1=(-1)^n*sin(n)/(n^2+1);
>> v1=symsum(s1,n,1,inf)
v1 = symsum(((-1)^n*sin(n))/(n^2 + 1), n, 1, Inf)参考资料:
[1] 天工在线. MATLAB2020从入门到精通·实战案例版[M]. 北京: 中国水利水电出版社, 2020.
相关文章:
(MATLAB)第十二章-数列与极限
目录 12.1 数列 12.1.1 数列求和 1. 累计求和函数sum() 2. 忽略NaN累计求和函数 nansum() 3. 求此元素位置之前的元素和函数cumsum() 4. 求梯形累计和函数cumtrapz() 12.1.2 数列求积 1. 元素连续相乘函数 prod() 2. 求累计积函数 cumprod() 3. 阶乘函数 ffactorial(n…...
OJ输入问题+准备
写在之前: 发现题目输入是这样的: 我的问题:如何通过空格分割这些输入的字符串并分别保存!!(C语言scanf好解决一点但我选择C....) C引入了ostringstream、istringstream、stringstream这三个类…...

软考高级:主动攻击和被动攻击概念和例题
作者:明明如月学长, CSDN 博客专家,大厂高级 Java 工程师,《性能优化方法论》作者、《解锁大厂思维:剖析《阿里巴巴Java开发手册》》、《再学经典:《Effective Java》独家解析》专栏作者。 热门文章推荐&am…...
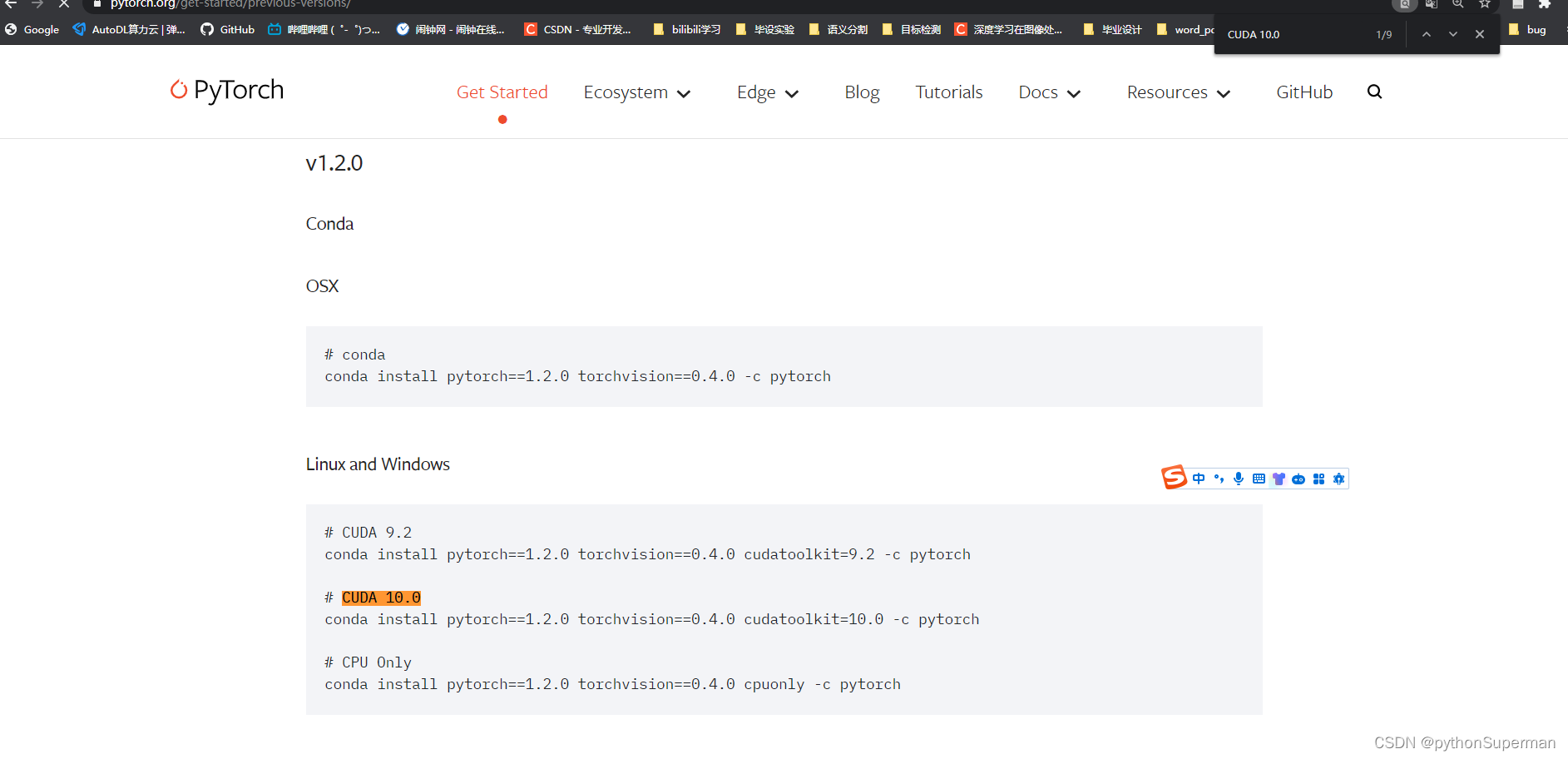
cuda python torch 虚拟环境配置
以下是Pytorch和CUDA对应的版本 以下是Pytorch和Python对应的版本 检查cuda与Python版本是否匹配 import torch print(torch.__version__) print(torch.cuda.is_available()) print(torch.empty(3,4,devicecuda))cuda 删除cuda conda uninstall cudatoolkit --forceconda u…...
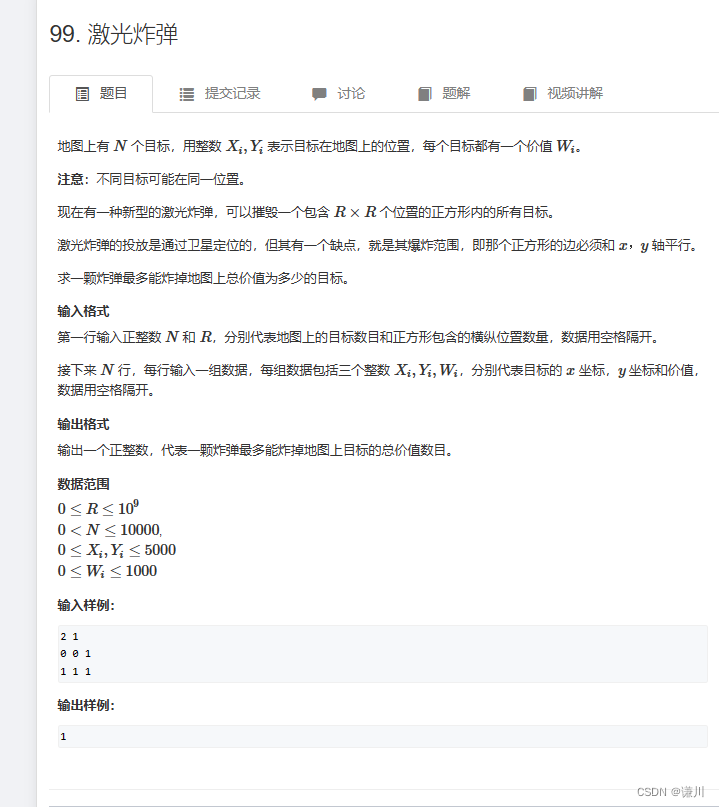
激光炸弹 刷题笔记
前置知识 二维前缀和 子矩阵的和 刷题笔记 {二维前缀和}-CSDN博客 思路 参考二维前缀和 将子矩阵的和 做成动态矩阵 一个个矩阵搜索 符合要求边长 矩阵中的元素和最大值 将x1,y1用i-k,j-k表示即可 x2,y2用i,j表示 代码 #include<iostream> #include<…...

Vue3学习记录(三)--- 组合式API之生命周期和模板引用
一、生命周期 1、简介 生命周期,指的是一个 Vue 实例从创建到销毁的完整阶段,强调的是一个时间段。 生命周期钩子函数,指的是 Vue 实例提供的内置函数,函数的参数为一个回调函数。这些钩子函数会在实例生命周期的某些固定…...
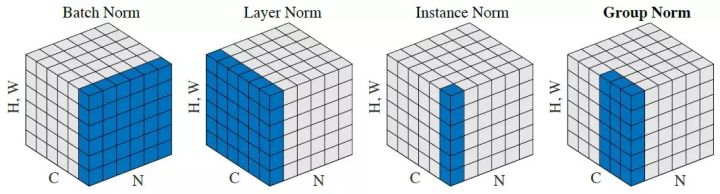
Batch Normalization和Layer Normalization和Group normalization
文章目录 前言一、Group normalization二、批量规范化(Batch Normalization)三、层规范化(Layer Normalization) 前言 批量规范化和层规范化在神经网络中的每个批次或每个层上进行规范化,而GroupNorm将特征分成多个组,并在每个组内…...

命名实体识别NER(综合代码示例)
一、命名实体识别发展方向 二、中文数据集 CCKS2017开放的中文的电子病例测评相关的数据。 评测任务一:https://biendata.com/competition/CCKS2017_1/ 评测任务二:https://biendata.com/competition/CCKS2017_2/ CCKS2018开放的音乐领域的实体识别任务…...

关于jQuery日历插件:daterangepicker
关于options singleDatePicker: false 双日历,true 单日历 timePicker:false 不显示时分秒,true 显示时分秒 timePickerIncreament:1 默认值 {singleDatePicker : false, //是否显示单日历框 dateLimit : { days : 30 }, //起…...

【贪心算法】最大子序和
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。 子数组是数组中的一个连续部分。 示例 1: 输入:nums [-2,1,-3,4,-1,2,1,-5,4] 输出:6…...
爬虫逆向网站案例
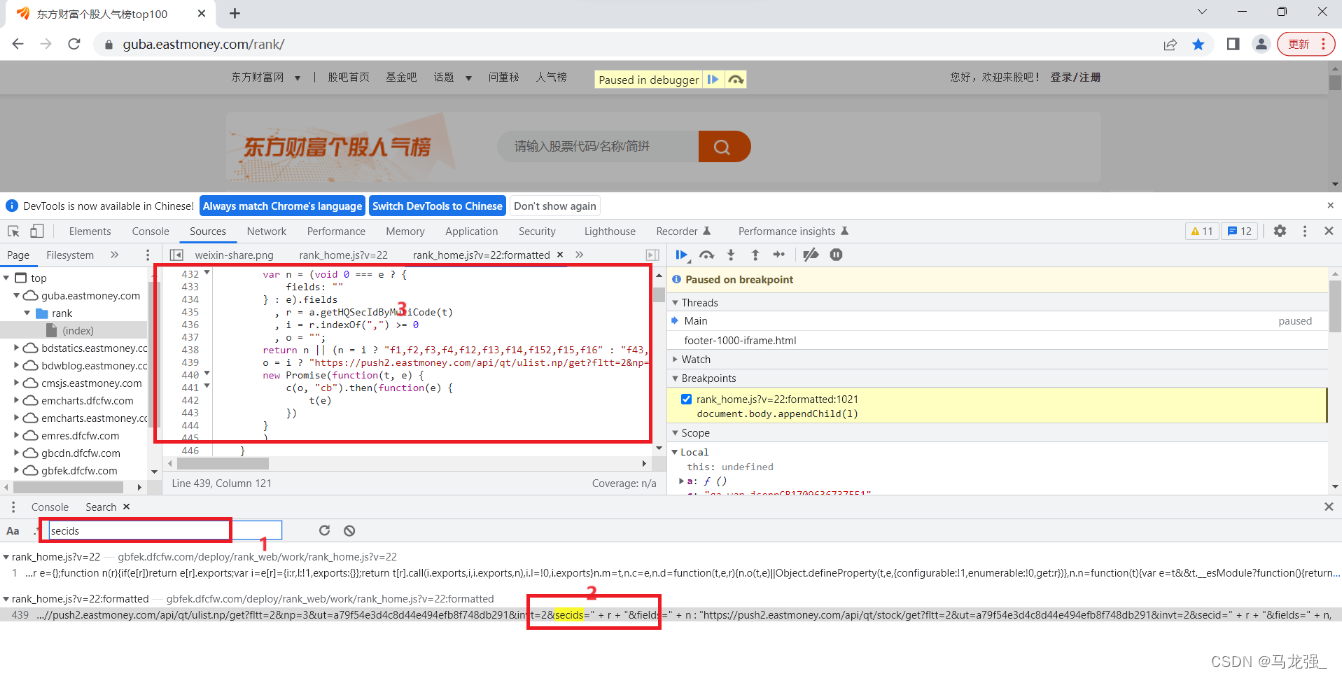
一、相关网页 东方财富人气排行榜 二、查找url 三、寻找curl并复制 四、打开Convert curl commands to code (curlconverter.com) 五、修改并执行代码 import requestscookies {st_si: 73974981954644,st_pvi: 39724919122964,st_sp: 2024-03-05%2018%3A27%3A22,st_inirUrl:…...

蓝桥杯复习之前缀和
题目链接:https://www.luogu.com.cn/problem/P8649 思路: 看到区间和,第一反应肯定是前缀和,我们求出前缀和后对前缀和数组每一个值模k,然后对一个数组的值查看前面有几个相同的,举个例子:…...
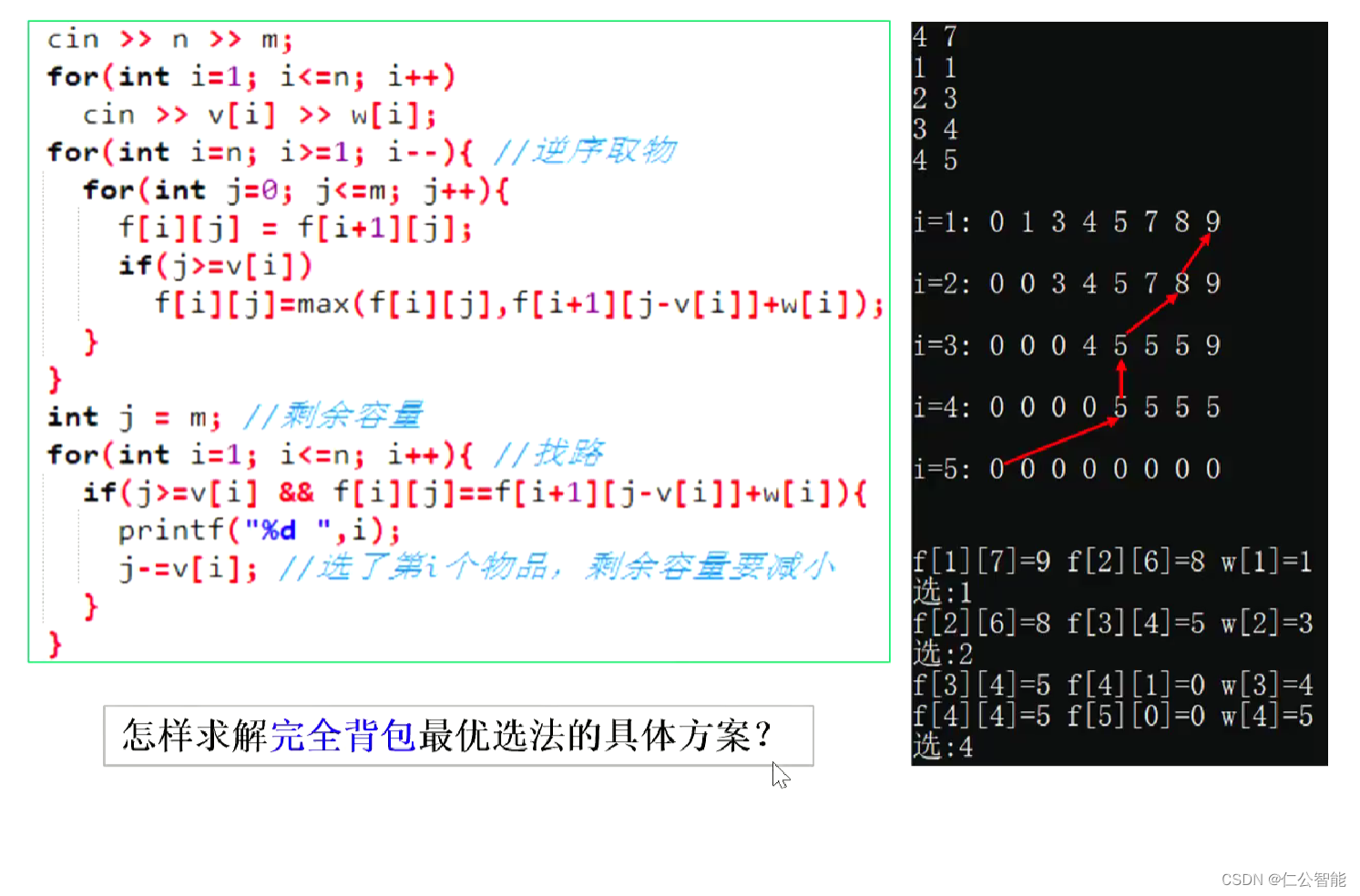
动态规划(算法竞赛、蓝桥杯)--背包DP求具体方案
1、B站视频链接:E20 背包DP 求具体方案_哔哩哔哩_bilibili #include <bits/stdc.h> using namespace std; const int N1010; int v[N],w[N]; int f[N][N],p[N][N];int main(){int n,m;cin>>n>>m;for(int i1;i<n;i)cin>>v[i]>>w[i…...

go写mysql取得自增字段值
场景:有多张表,依据其中一张表的自增字段取得 id 值作为对象ID,然后使用这个Id插入到其他它表中。 如下一张 MySQL 的 innodb 表 X,用 go 编写程序,不指定 a 的值,指定 b 和 c 的值,往表 X 插入…...

Vue 3的Composition API和vue2的不同之处
Vue 3的Composition API是Vue.js框架的一个重要更新,它提供了一种新的组件逻辑组织和复用方式。在Vue 2中,我们通常使用Options API(data、methods、computed等)来组织组件的逻辑,但这种组织方式在处理复杂组件时可能会…...

go语言基础 -- 面向对象编程
go语言面向对象编程思想 面向对象编程离不开封装、继承、多态三个特性,go语言与其他c、java不太一样,没有类的概念,面向对象的实现也有些区别,下面分别描述。 go语言封装 结构体中字段如欲对外隐藏,首字母小写&…...
HarmonyOS—编译构建概述
编译构建是将应用/服务的源代码、资源、第三方库等,通过编译工具转换为可直接在硬件设备上运行的二进制机器码,然后再将二进制机器码封装为HAP/APP软件包,并为HAP/APP包进行签名的过程。其中,HAP是可以直接运行在模拟器或真机设备…...
下载element-ui 资源,图标 element-icons.woff,element-icons.ttf 无法解码文件字体
css下载地址:https://unpkg.com/element-ui2.15.14/lib/theme-chalk/index.css js下载地址:https://unpkg.com/element-ui2.15.14/lib/index.js 图标及文字文件下载地址: element-icons.woff:: https://unpkg.com/element-…...
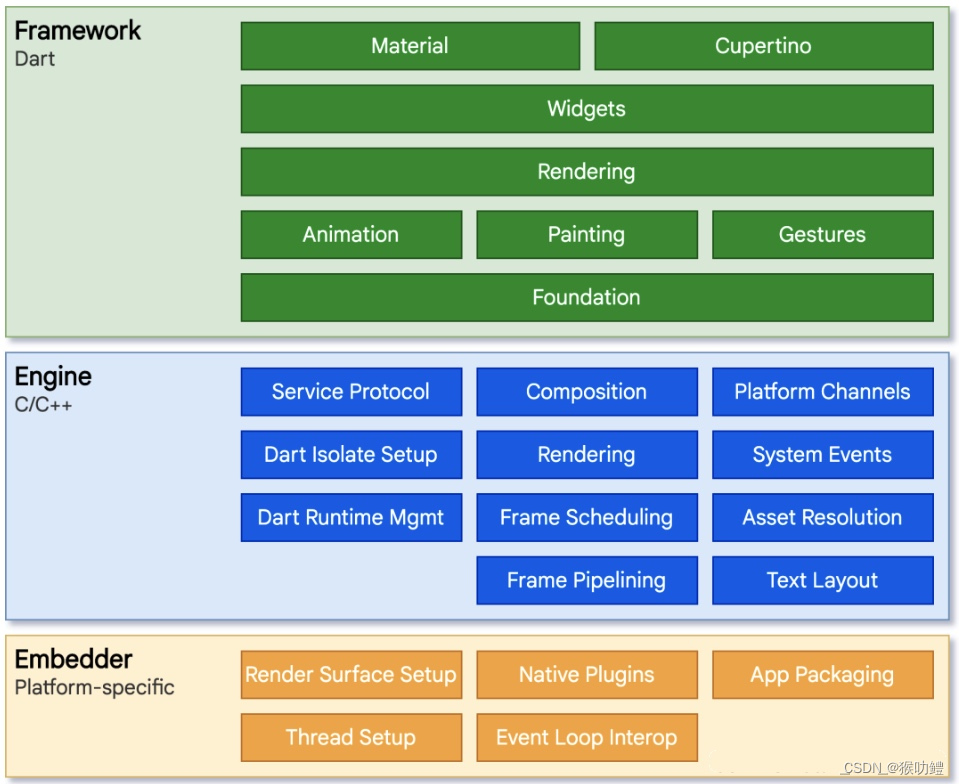
Flutter整体框架
Flutter整体框架由三部分组成:Framework、Engine和Embedder。 Framework Framework提供了一个用 Dart 语言编写的现代、反应式框架,由许多抽象的层级组成。它包括一套丰富的布局、动画、绘制、手势UI组件及配套代码,以及更基础的异步、文件、…...

JVM堆内存中新生代晋升到老年代的条件
1. 一般年龄判断 当对象在Eden区中经过第一次 Minor GC 后,如果仍然存活,则会被移动到 From Survivor 区,并且对象的年龄设为 1。每经过一次 Minor GC,存活下来的对象年龄加 1,若存活对象在 From Survivor 区的年龄达…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...
