倍增算法C++
倍增
倍增算法是一种优化算法,通常用于某些需要高效计算指数幂的场景。它基于分治的思想,通过反复求平方来实现快速计算指数幂的目的。在实际应用中,倍增算法经常用于解决最近公共祖先问题、二分查找等。
1、快速幂详解
ksm核心代码

倍增就是基于二进制的指数倍相乘,使得效率更高。任何一个数的幂都可以看作二进制来计算。
ll ksm(ll a,ll n){ll r=1;while(n!=0){if(n&1){r*=a;}a=a*a;n=n>>1;}return r;
}
简单应用:
- 计算a^n mod m
- 计算斐波那契数列第n项
- 将线性变换重复n次
注:矩阵的乘法计算
2、链式前向星举例
2.1、图
关于图的定义方式:
struct Edge {int next; // 下一条边的编号int to; // 这一条边的终点int w; // 权值
} e[maxn];
一般的输入方式都是:u -> v w 边 边 权
ll tot, head[maxn];
void add(ll u, ll v, ll w) {++tot; // 加入一条新边的编号e[tot].next = head[u]; // 新的边插在原来的第一个位置,所以next指向原来的head[u]e[tot].w = w;e[tot].to = v; // 下一条边head[u] = tot; // 新的边成为第一条变了
}
代码案例:
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);
using namespace std;
using ll = long long;
#define maxn 110001
struct Edge {int next; // 下一条边的编号int to; // 这一条边的终点int w; // 权值
} e[maxn];
ll tot, head[maxn];
void add(ll u, ll v, ll w) {++tot; // 加入一条新边的编号e[tot].next = head[u]; // 新的边插在原来的第一个位置,所以next指向原来的head[u]e[tot].w = w;e[tot].to = v; // 下一条边head[u] = tot; // 新的边成为第一条变了
}
int main() {IOS;// 添加边add(1, 2, 10);add(1, 3, 20);add(2, 4, 30);add(3, 4, 40);add(4, 5, 50); // 打印图的邻接表for (int i = 1; i <= 5; ++i) {cout << "Vertex " << i << ": ";for (int j = head[i]; j != 0; j = e[j].next) {cout << "(" << e[j].to << ", " << e[j].w << ") ";}cout << endl;}return 0;
}
2.2、树
LCA问题
int n;cin>>n;vector<vector<int>> graph(n+1);for(int i=1;i<n;i++){//n-1 条边int u,v;cin>>u>>v;graph[i].push_back(u);graph[i].push_back(v);//邻接矩阵}//倍增数组vector<array<int,21>> fa(n+1);//array<int,21> 固定的数组大小21vector<int> dep(n+1);//深度function<void(int,int)> dfs = [&](int x,int f){fa[x][0]=f;for(int i=1;i<=20;i++){fa[x][i]=fa[fa[x][i-1]][i-1];}//遍历数组for(const auto& tox:graph[x]){if(tox==f)continue;dep[tox]=dep[x]+1;dfs(tox,x);}};dfs(1,0);auto glca = [&](int x,int y){if(dep[x]<dep[y])swap(x,y);int d=dep[x]-dep[y];for(int i=20;i>=0;i--){if(d>>i & 1)x=fa[x][i];}if(x==y)return x;for(int i=20;i>=0;i--){if(fa[x][i] != fa[y][i]){x=fa[x][i];y=fa[y][i];}}return fa[x][0];};
相关文章:

倍增算法C++
倍增 倍增算法是一种优化算法,通常用于某些需要高效计算指数幂的场景。它基于分治的思想,通过反复求平方来实现快速计算指数幂的目的。在实际应用中,倍增算法经常用于解决最近公共祖先问题、二分查找等。 1、快速幂详解 ksm核心代码 倍增就是…...

uniapp制作--进步器的选择
介绍: 进步器的选择,一般用于商城购物选择物品数量的场景 注意:该输入框只能输入大于或等于0的整数 效果展示: 代码展示: 以下是一个简单的购物车页面示例,包括选择商品和显示数量的功能: 在这个示例中…...

前端高频面试--查缺补漏篇
什么是进程和线程,有什么区别 进程:进程是程序的一次执行过程,是动态的过程,有自身产生、存在、消亡的过程。 线程:线程由进程创建,是进程的一个实体。一个进程可以拥有多个线程。 举个例子:…...

【计算机学习】-- 网页视频加速
系列文章目录 文章目录 系列文章目录前言一、开发者选项二、定义和用法1.基础语法:2.什么是uncaught TypeError:Cannot read properties of null? 二、开发者工具面板:1.Elements面板:2.Console面板: 总结 前言 一、开发者选项 …...

系统运维-Linux配置C、C++、Go语言编译环境
C yum install gcc -y #安装gcc编译器 gcc --version #验证环境gcc (GCC) 11.3.1 20221121 (Red Hat 11.3.1-4) Copyright (C) 2021 Free Software Foundation, Inc. This is free software; see the source for copying conditions. There is NO warranty; not even f…...
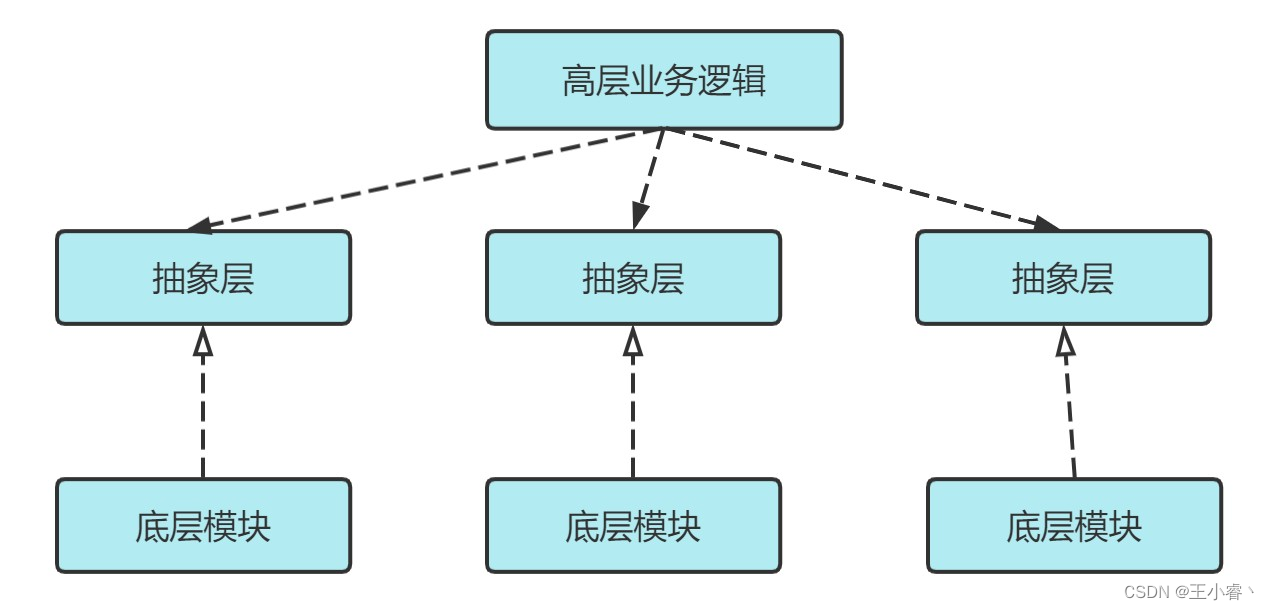
【设计模式】(二)设计模式六大设计原则
一、 设计原则概述 设计模式中主要有六大设计原则,简称为SOLID ,是由于各个原则的首字母简称合并的来(两个L算一个,solid 稳定的),六大设计原则分别如下: 1、单一职责原则(Single Responsibitity Principle&#…...

go-zero官网
go-zero 是一个集成了各种工程实践的 web 和 rpc 框架。通过弹性设计保障了大并发服务端的稳定性,经受了充分的实战检验。 go-zero官网:go-zero 缩短从需求到上线的距离...
)
Redis的应用场景以及常见问题(持续更新)
一、使用场景 1,在大型的秒杀库存扣减,app首页流量高峰,很容易将传统的关系型数据库(mysql,oracle等)给压垮 2,还有很多没必要持久化的数据,比如说短信验证码,点赞数等 3,…...

前端添加压缩包内文件名称校验
1. tar包内文件名称校验 1. 读取tar包内所有的文件名称 export class TarReader {fileInfo: any[]buffer: string | ArrayBufferconstructor() {this.fileInfo []}readFile(file) {return new Promise(resolve > {const reader new FileReader()reader.onload event &g…...
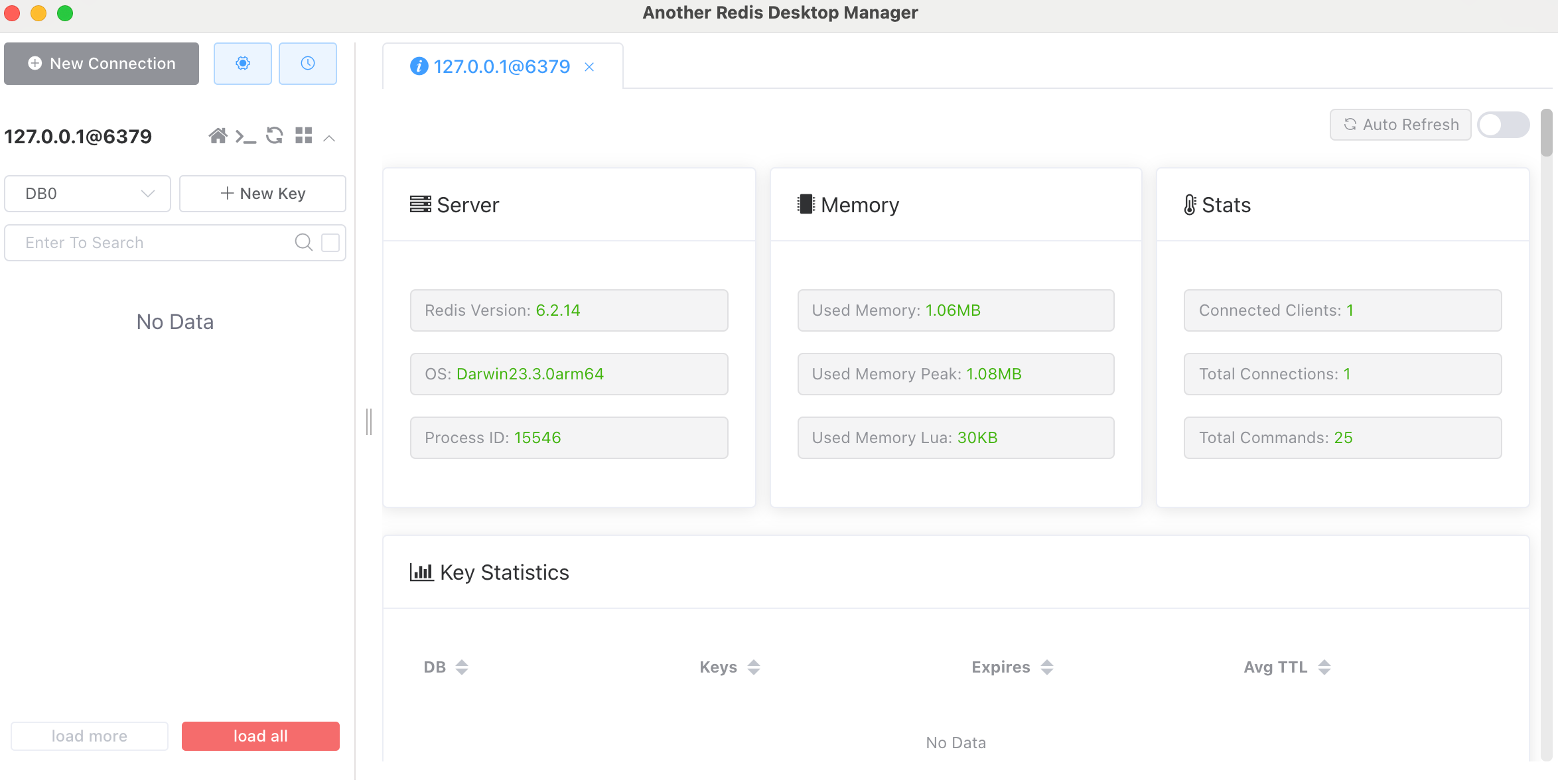
redis02 安装
官网下载 传送门https://redis.io/download/#redis-downloads 安装Redis mac m1安装 下载你需要版本的软件包放到指定的目录下进行解压 cd 到解压好的redis目录 运行下面的命令进行编译测试 sudo make test 中途可能会提示你安装make工具,按提示安装即可&…...
)
#QT(QT时钟)
1.IDE:QTCreator 2.实验 3.记录 qtime(qt的时间类) qtimer(qt的定时类) 4.代码 widget.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QTime> // #include <QTimer&g…...

T-RAG:结合实体检测的增强检索生成模型
内容摘要: T-RAG是一种新的大型语言模型(LLM)应用框架,在保证数据隐私的同时,提高了对私有企业文档的问答系统性能。T-RAG通过结合已有的增强检索生成(RAG)框架、自定义的开源语言模型以及一个实…...

u-boot: NAND 驱动简介
文章目录 1. 前言2. NAND 初始化3. 访问 NAND 设备3.1 查看 NAND 设备信息3.1.1 查看 NAND 设备基本信息3.1.2 查看 NAND 设备 MTD 分区3.1.3 查看 NAND 设备坏块 3.2 NAND 擦除操作3.3 NAND 写操作3.4 NAND 读操作3.5 其它 NAND 操作 1. 前言 限于作者能力水平,本…...

史上最全的大数据开发八股文【自己的吐血总结】
自我介绍 我本硕都是双非计算机专业,从研一下开始学习大数据开发的相关知识,从找实习到秋招,我投递过100公司,拿到过10的offer,包括滴滴、字节、蚂蚁、携程、蔚来、去哪儿等大厂(岗位都是大数据开发&#…...
数据库学习案例20240304-mysql数据库案例总结(碎片,统计信息)
1 表中的碎片 在InnoDB中删除行的时候,这些行只是被标记为“已删除”,而不是真正从物理存储上进行了删除,因而存储空间也没有真正被释放回收。InnoDB的Purge线程会异步地来清理这些没用的索引键和行。但是依然没有把这些释放出来的空间还给操…...

【小白友好】LeetCode 删除并获得点数
基础题 打家劫舍https://leetcode.cn/problems/house-robber/ 小白解法 删除nums[i]就会使得所有nums[i]-1和nums[i]1的值都消失,手写了几个,发现找来找去不方便,还不如先排个序,然后这样nums[i]-1和nums[i]和nums[i]1就能靠在…...

c#委托、lambda、事件
Lambda Lambda表达式是一种匿名函数,Lambda表达式通常以箭头“>”分隔左侧的输入和右侧的输出。 (parameter_list) > { statement_block } parameter_list 是由一个或多个参数组成的逗号分隔列表,每个参数都包括类型和名称,可以为空。…...

每日一练——9×9乘法表
#include<stdio.h>int main() {int i 0; //乘数定义for (i 1; i < 9; i) //循环1到9 {int j 0;//被乘数定义for (j 1; j < i; j) //循环被乘数1到9{printf("%d*%d%2d ", i, j, i * j); 乘法}printf("\n"); 换行} return 0; }...

大白话解析LevelDB:ShardedLRUCache
文章目录 Cache 接口定义ShardedLRUCache 的实现ShardedLRUCache 的构造函数ShardedLRUCache::Insert(const Slice& key, void* value, size_t charge, void (\*deleter)(const Slice& key, void* value))ShardedLRUCache::Lookup(const Slice& key)ShardedLRUCach…...

GDOI2024游记
Day0 中午一点钟从学校出发去东莞,大概坐了一个多小时车,两点半多到酒店。住的八方精选酒店(ljh说他们住九方精选酒店,乐),说的是景区酒店,但打开外窗,近处是简陋的阳台,…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

DiscuzX3.5发帖json api
参考文章:PHP实现独立Discuz站外发帖(直连操作数据库)_discuz 发帖api-CSDN博客 简单改造了一下,适配我自己的需求 有一个站点存在多个采集站,我想通过主站拿标题,采集站拿内容 使用到的sql如下 CREATE TABLE pre_forum_post_…...

高防服务器价格高原因分析
高防服务器的价格较高,主要是由于其特殊的防御机制、硬件配置、运营维护等多方面的综合成本。以下从技术、资源和服务三个维度详细解析高防服务器昂贵的原因: 一、硬件与技术投入 大带宽需求 DDoS攻击通过占用大量带宽资源瘫痪目标服务器,因此…...

倒装芯片凸点成型工艺
UBM(Under Bump Metallization)与Bump(焊球)形成工艺流程。我们可以将整张流程图分为三大阶段来理解: 🔧 一、UBM(Under Bump Metallization)工艺流程(黄色区域ÿ…...

深入浅出WebGL:在浏览器中解锁3D世界的魔法钥匙
WebGL:在浏览器中解锁3D世界的魔法钥匙 引言:网页的边界正在消失 在数字化浪潮的推动下,网页早已不再是静态信息的展示窗口。如今,我们可以在浏览器中体验逼真的3D游戏、交互式数据可视化、虚拟实验室,甚至沉浸式的V…...

拟合问题处理
在机器学习中,核心任务通常围绕模型训练和性能提升展开,但你提到的 “优化训练数据解决过拟合” 和 “提升泛化性能解决欠拟合” 需要结合更准确的概念进行梳理。以下是对机器学习核心任务的系统复习和修正: 一、机器学习的核心任务框架 机…...
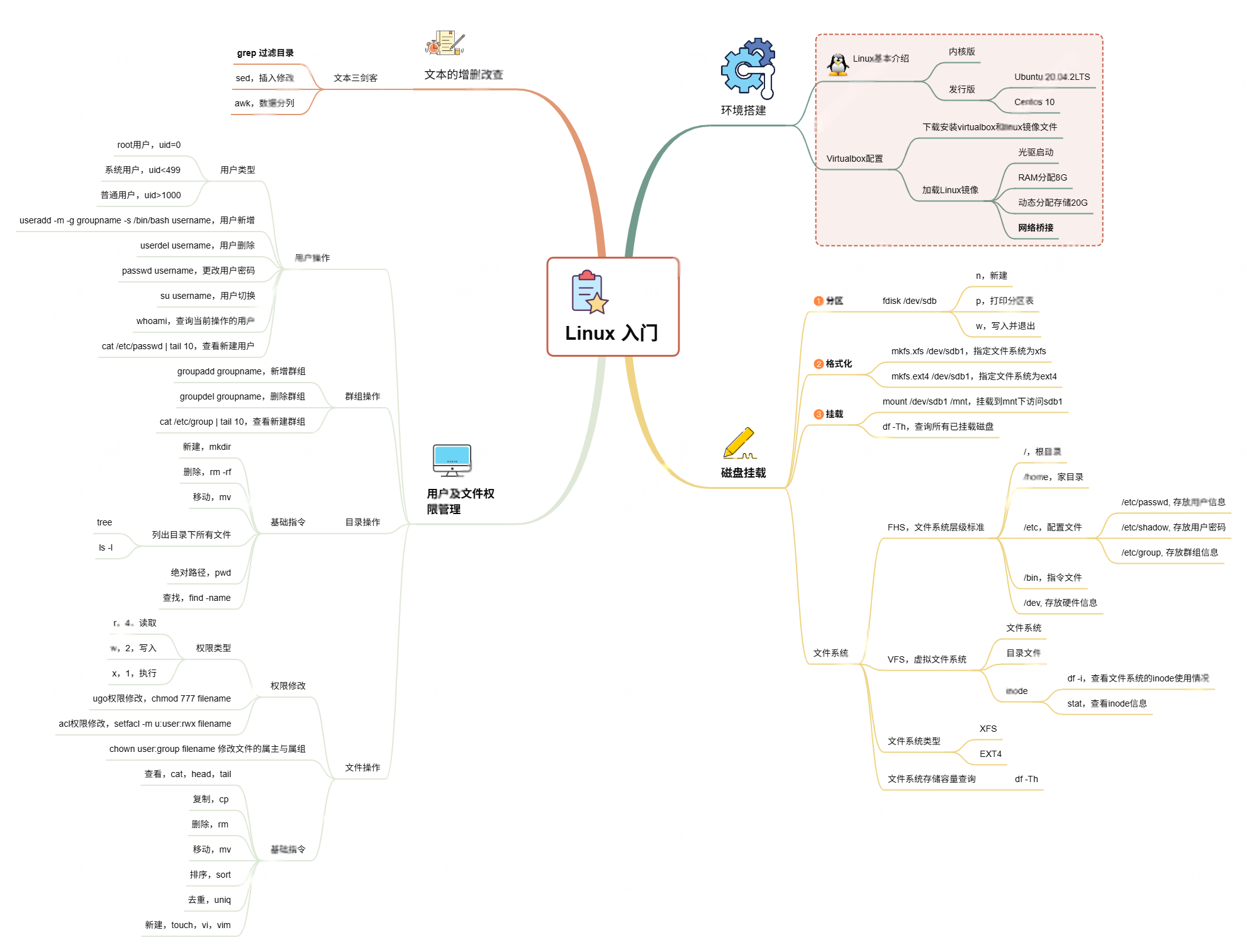
Linux入门课的思维导图
耗时两周,终于把慕课网上的Linux的基础入门课实操、总结完了! 第一次以Blog的形式做学习记录,过程很有意思,但也很耗时。 课程时长5h,涉及到很多专有名词,要去逐个查找,以前接触过的概念因为时…...
加密芯片与MCU协同工作的典型流程)
SE(Secure Element)加密芯片与MCU协同工作的典型流程
以下是SE(Secure Element)加密芯片与MCU协同工作的典型流程,综合安全认证、数据保护及防篡改机制: 一、基础认证流程(参数保护方案) 密钥预置 SE芯片与MCU分别预置相同的3DES密钥(Key1、Key2…...
