浅谈马尔科夫链蒙特卡罗方法(MCMC)算法的理解
1.解决的问题
计算机怎么在任意给定的概率分布P上采样?首先可以想到把它拆成两步:
(1)首先等概率的从采样区间里取一个待定样本x,并得到它的概率为p(x)
(2)然后在均匀分布U[0,1]上取一个值,如果这个值高于了样本出现的概率p(x),那么就舍弃掉这个待定样本,如果低于或等于这个值就保留。
不断重复这个步骤,我们就能得到满足概率分布P的样本X。
这个方法看似有效,但存在一个致命的问题,那就是慢,因为概率p的均值,随着采样的区域增大而减小【如果P是多维概率分布,那么随着维度不断增大,那么这个值将趋近于0,也就是维度灾难】,那么就意味着这个样本被保留下来的概率非常小。
那么怎么改进?
我们把上述的第(2)步改一下,不再用均匀U[0,1]进行采样,而是用U[0,max(p)],而选取的规则变为,如果从均匀分布U[0,max(p)]里取得的值u高于p(x),那么就保留该样本。
这样能够保证,至少有一个可能出现的样本在概率区间接受率为1。
这种改进比第一种的命中率要高上不少,如果p是均匀分布,那么采样命中率将是100%,当然如果采样是均匀分布,那么我直接取就好了,没必要多这么一步。
那么在此之上还有什么改进呢?
你自然能想到,我们不再用均匀分布U来计算样本是否可以保留,我们找一个好实现的概率分布Q,这个Q要和分布P相似,我们放缩该概率密度函数,使得min(q)>max(p)。
这样一来,命中率就又提高了,而且可以预想到,如果概率分布q=p那么采样命中率就会是100%,但这自然不可能。
那么有没有一种方法可以让采样的命中率是100%呢?
有,就是MCMC,在MCMC中,所有样本都是有效采样。而原理则是用频率取代概率。
2.MCMC
假设我们手里有个小球,每隔一秒就会变一种颜色(包括当前颜色),一段时间后,我们统计每种颜色的时间,就可以得到,各颜色出现的概率。
而这就是MCMC的原理,我们要做的是借助马尔可夫链,实现这样一个小球。
我们给小球输入一个指令,给定它每种颜色出现的概率,也就是P。
这时候小球内部有个状态机会来实现这个概率,首先会按照颜色的数量建立状态,同时每种状态之间会有线路连接,且每种状态之间都是相互可达的,即连通。
这时候有钢珠在每种状态里游走,钢珠到了哪种状态,哪种状态代表的灯就会亮起。
好了,如何让小球的灯能够以某种稳定的频率让灯亮起。
研究发现,只要让两两状态之间转换的概率与对方状态的概率乘积相等。
即P(A)Q(A->B)=P(B)Q(B->A),这就是马尔科夫链细致平衡条件,A和B代表任意两个状态。Q(A-B)是状态A到状态B的转移概率。
这时候,我们只要跟随钢珠在各状态之间的游走,记录下状态值即样本值,就能完成采样。
具体步骤如下,
(1)记录钢珠初始值状态X1。
(2)随机选择一个目标状态。
(3)查看抵达目标状态的转移概率。
(4)从U[0,1]中采一个值,如果值大于转移概率,那么状态不变,如果小于或等于转移概率,那么状态转化为目标状态。
重复如上步骤,就能得到一个服从P分布的样本了。
但这个算法虽然没有无效采样,但状态A转移到状态的转移概率过低,那么就会长时间卡在这一种状态。那么有没有方法改进呢。
当然有,那就是等比例缩放平衡方程两边的转移概率,P(A)Q(A->B)=P(B)Q(B->A)。
这里有个限制,那就是不能破坏转移概率小于或等于1概率特性,同时也不能破坏平衡方程本身。
那么我们能找到的一个缩放系数就是MAX[P(B->A),P(A->B)],两边同时除以该系数。
则有P(A)MIN[1,Q(A->B)/Q(B->A)] = P(B)MIN[1,Q(A->B)/Q(B->A)]
这样就能保证至少有一边可以必定转化为另一边。
到这里MCMC就算比较完整了。
问题就是Q怎么选。
这里有两种方案,一个就是Q任取,只要满足转移矩阵的要求,然后补一个系数配平方程
即: P(A)Q(A->B)*[P(B)Q(B->A)]=P(B)Q(B->A)*[P(A)Q(A->B)],
缩放后有:
P(A)Q(B->A)*MIN[1,P(B)Q(B->A)/P(B)Q(B->A)] = P(B)Q(B->A)*MIN[1,P(A)Q(A->B)/P(B)Q(B->A)]
另一种那就是选Q(A->B) = P(B),Q(B->A)=P(A)。
前者是HM的思想,配平的系数的使用方法类比前一节的转移接受率。
后者是Gibbs的思想。
具体实现有很多细节,可以看下面推荐的教学视频,这里推荐先看P6
机器学习-白板推导系列-蒙特卡洛方法5(Monte Carlo Method)- 再回首_哔哩哔哩_bilibili
相关文章:
浅谈马尔科夫链蒙特卡罗方法(MCMC)算法的理解
1.解决的问题 计算机怎么在任意给定的概率分布P上采样?首先可以想到把它拆成两步: (1)首先等概率的从采样区间里取一个待定样本x,并得到它的概率为p(x) (2)然后在均匀分布U[0,1]上取一个值&a…...

2403C++,C++20协程库
原文 基于C20协程的http库--cinatra cinatra是基于C20无栈协程实现的跨平台,仅头,高性能,易用的http/https库(http1.1),包括httpserver和httpclient,功能完备,不仅支持最普通的getpost等请求,还支持restfulapi,websocket,chunked,ranges,multipart,静态文件服务和反向代理等功…...

mybatis动态加载mapper.xml
mybatis动态加载mapper.xml mybatis动态加载mapper.xml、springboot mybatis动态加载mapper.xml 教程连接:https://blog.csdn.net/weixin_44480167/article/details/136356398...
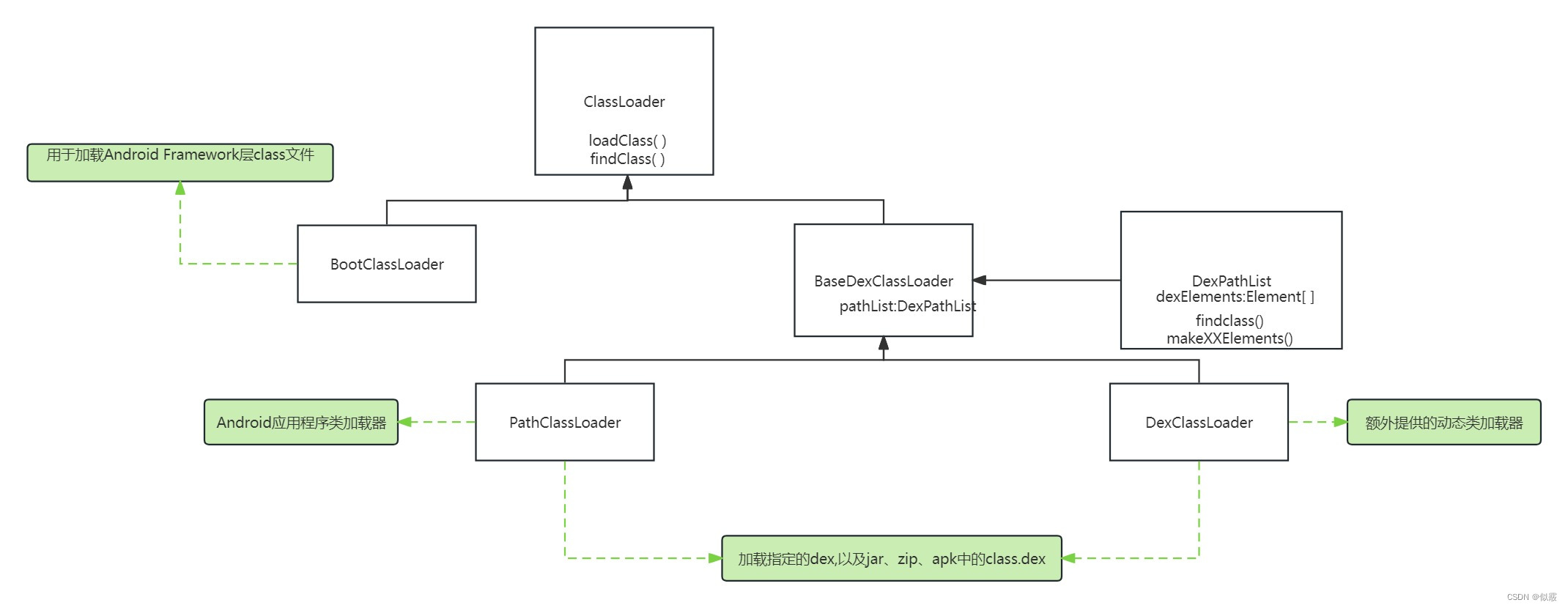
安卓类加载机制
目录 一、ClassLoader介绍二、双亲委托机制三、类的加载过程 一、ClassLoader介绍 任何一个 Java 程序都是由一个或多个 class 文件组成,在程序运行时,需要将 class 文件加载到 JVM 中才可以使用,负责加载这些 class 文件的就是 Java 的类加…...

FPGA高端项目:FPGA基于GS2971的SDI视频接收+HLS图像缩放+多路视频拼接,提供4套工程源码和技术支持
目录 1、前言免责声明 2、相关方案推荐本博已有的 SDI 编解码方案本方案的SDI接收转HDMI输出应用本方案的SDI接收图像缩放应用本方案的SDI接收纯verilog图像缩放纯verilog多路视频拼接应用本方案的SDI接收HLS动态字符叠加输出应用本方案的SDI接收HLS多路视频融合叠加应用本方案…...

[计算机网络]--五种IO模型和select
前言 作者:小蜗牛向前冲 名言:我可以接受失败,但我不能接受放弃 如果觉的博主的文章还不错的话,还请点赞,收藏,关注👀支持博主。如果发现有问题的地方欢迎❀大家在评论区指正 目录 一、五种IO…...
【力扣经典面试题】14. 最长公共前缀
目录 一、题目描述 二、解题思路 三、解题步骤 四、代码实现(C版详细注释) 五、总结 欢迎点赞关注哦!创作不易,你的支持是我的不竭动力,更多精彩等你哦。 一、题目描述 编写一个函数来查找字符串数组中的最长公共前缀。…...
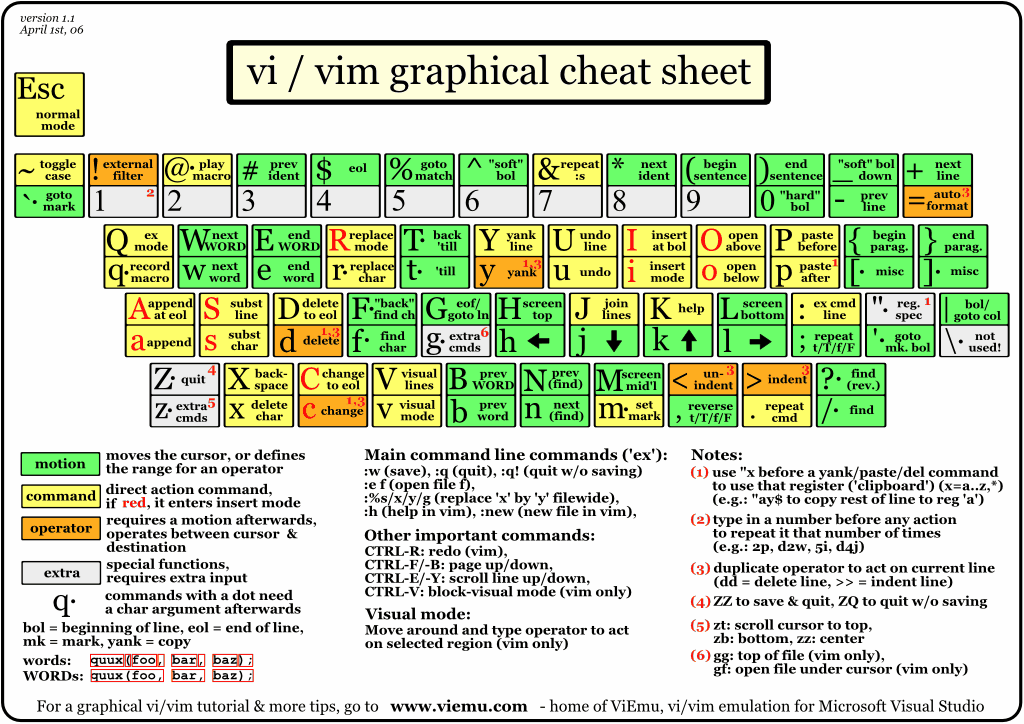
Linux操作系统的vim常用命令和vim 键盘图
在vi编辑器的命令模式下,命令的组成格式是:nnc。其中,字符c是命令,nn是整数值,它表示该命令将重复执行nn次,如果不给出重复次数的nn值,则命令将只执行一次。例如,在命令模式下按j键表…...
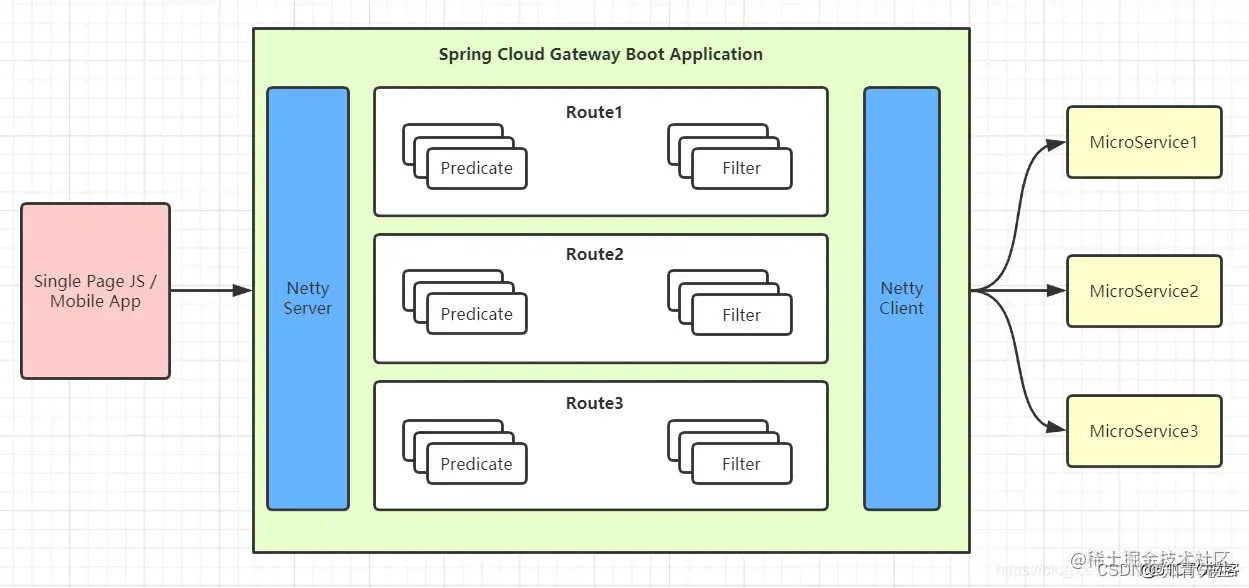
SpringCloudGateway工作原理与链路图
SpringCloudGateway基本介绍 Spring Cloud Gateway 构建于Spring Boot 2.x、 Spring WebFlux和Project Reactor之上。因此,在使用 Spring Cloud Gateway 时,您可能不会应用许多熟悉的同步库(例如 Spring Data 和 Spring Security)和模式。 Spring Cloud Gateway 需要 Sprin…...

VUE2与VUE3之间的主要区别
当谈到 Vue.js 的版本时,Vue 2 和 Vue 3 是最常被提及的两个版本。下面是 Vue 2 和 Vue 3 之间的一些主要区别: 1. 性能提升: Vue 3 在底层核心重写了响应式系统,采用了 Proxy 对象,大幅提高了性能。Vue 3 还引入了静…...

CSS浮动实战,经典好文
零基础学web前端开发要怎么去学? 首先要学习的就是基础知识:html、css和JavaScript。HTML是内容,CSS是表现,JavaScript是行为。前端开发的门槛其实非常低,与服务器端语言先慢后快的学习曲线相比,前端开发的学习曲线是…...
如何搭建Nacos集群
1.搭建Nacos集群 众所周知,在实际的工作中,Nacos的生成环境下一定要部署为集群状态 其中包含3个nacos节点,然后一个负载均衡器代理3个Nacos。这里负载均衡器可以使用nginx。 我们计划的集群结构: 我就直接在本机上开三个Nacos来搭…...
未来已来!AI大模型引领科技革命
未来已来!AI大模型正以惊人的速度引领着科技革命。随着科技的发展,人工智能在各个领域展现出了非凡的能力和潜力,大模型更是成为了科技领域的明星。从自然语言处理到图像识别,从智能推荐到语音识别,大模型的应用正在改…...
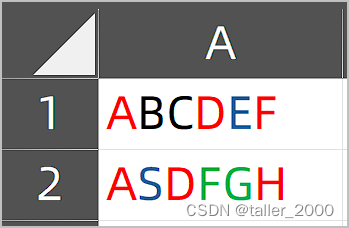
VBA如何记录单元格中字符内容和格式
实例需求:Excel单元格中的字符可以设置不同的字体格式(大小、颜色等),有时需要将这些信息保存起来,以便于后续代码的处理(例如替换后恢复原字体颜色,或者统计某种指定格式字符个数等等ÿ…...
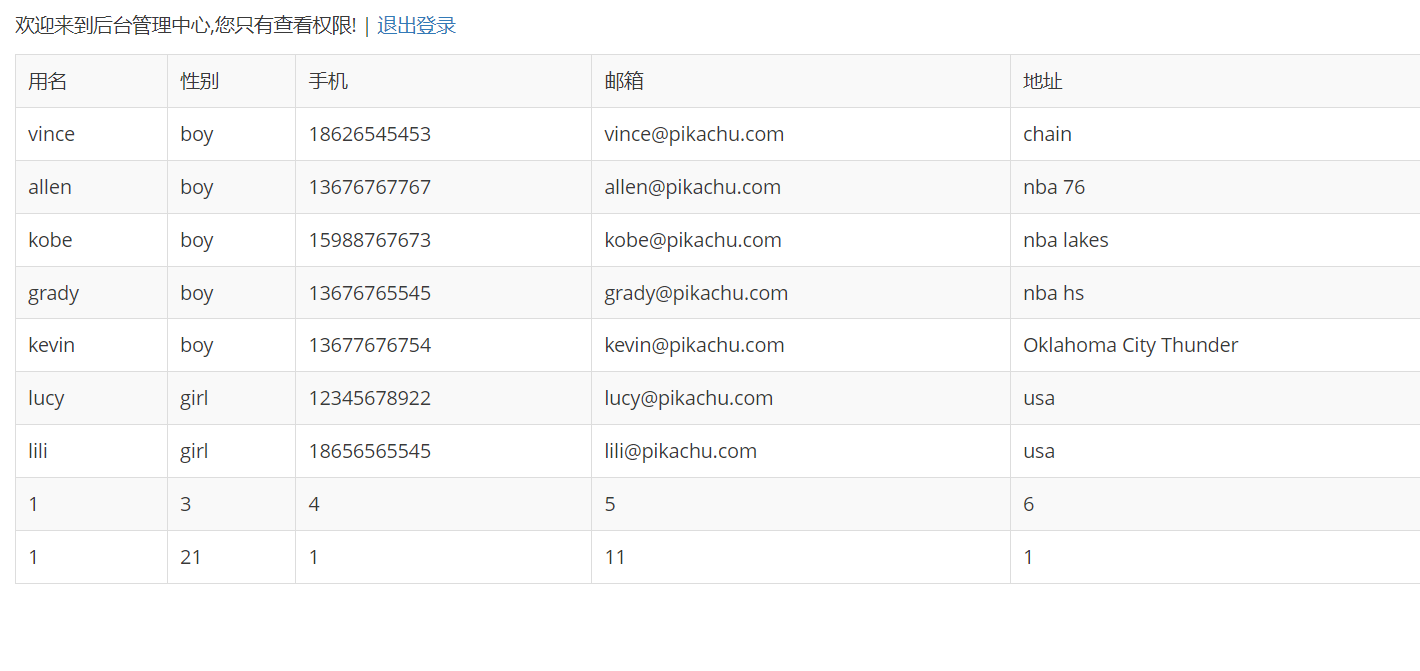
逻辑漏洞(pikachu)
#水平,垂直越权,未授权访问 通过个更换某个id之类的身份标识,从而使A账号获取(修改、删除)B账号数据 使用低权限身份的账号,发送高权限账号才能有的请求,获得其高权限操作 通过删除请求中的认…...
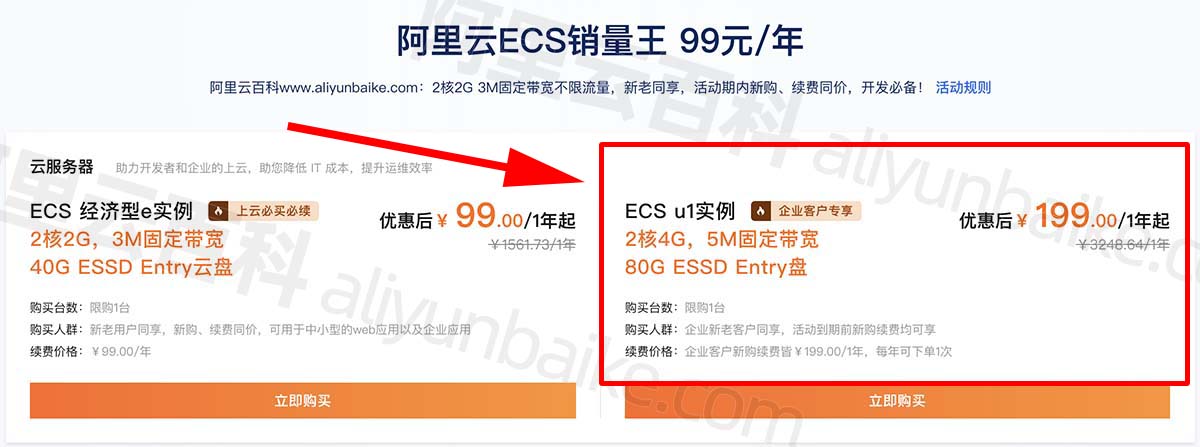
阿里云服务器2核4G多少钱?支持多少在线?并发数性能测试
阿里云2核4G服务器多少钱一年?2核4G配置1个月多少钱?2核4G服务器30元3个月、轻量应用服务器2核4G4M带宽165元一年、企业用户2核4G5M带宽199元一年。可以在阿里云CLUB中心查看 aliyun.club 当前最新2核4G服务器精准报价、优惠券和活动信息。 阿里云官方2…...

粘包与拆包
优质博文:IT-BLOG-CN 一、粘包出现的原因 服务端与客户端没有约定好要使用的数据结构。Socket Client实际是将数据包发送到一个缓存buffer中,通过buffer刷到数据链路层。因服务端接收数据包时,不能断定数据包1何时结束,就有可能出…...
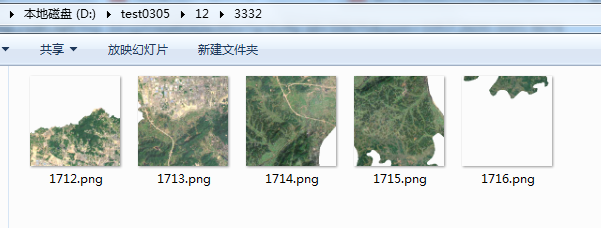
基于QGIS的研究区域遥感影像裁切下载方法-以岳麓区为例
目录 前言 一、数据说明 1、遥感影像 2、矢量范围 二、按矢量范围导出 1、第一步、导出影像 2、第二步、设置输出格式 3、设置裁切范围 4、设置分辨率 三、按矢量范围掩膜 1、第一步、打开裁剪工具 2、第二步、参数设置 编辑 3、执行掩膜 四、webgis支持 1、生成运行…...

YOLOv8-Openvino-ByteTrack【CPU】
纯检测如下: YOLOv5-Openvino和ONNXRuntime推理【CPU】 YOLOv6-Openvino和ONNXRuntime推理【CPU】 YOLOv8-Openvino和ONNXRuntime推理【CPU】 YOLOv9-Openvino和ONNXRuntime推理【CPU】 注:YOLOv8和YOLOv9代码内容基本一致! 全部代码Github&…...
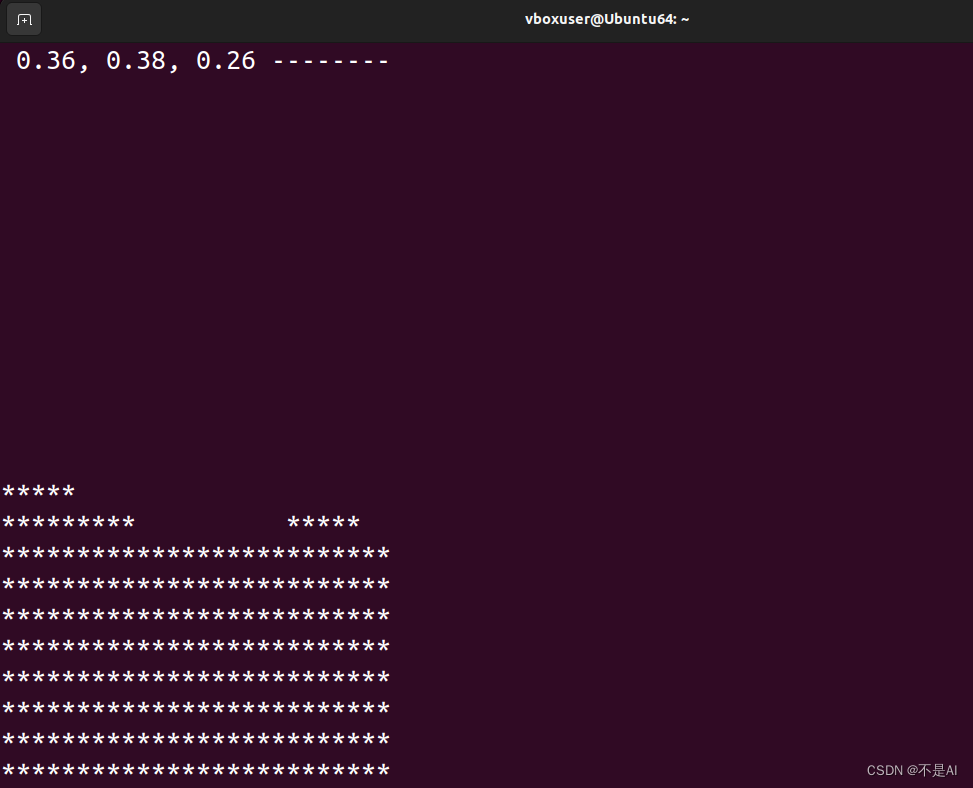
【Linux命令】tload
tload 显示系统负载状况。 详细 tload命令以图形化的方式输出当前系统的平均负载到指定的终端。假设不给予终端机编号,则会在执行tload指令的终端机显示负载情形。 语法 tload (选项)(参数)选项 -s : 指定闲时的…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...
