图论例题解析
1.图论基础概念
概念
(注意连通非连通情况,+1节点)
无向图: 度是边的两倍(没有入度和出度的概念)
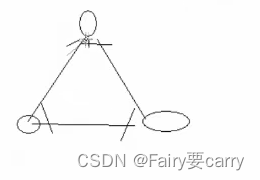
1.完全图: 假设一个图有n个节点,那么任意两个节点都有边则为完全图
2.连通图:是指任意两个结点之间都有一个路径相连。
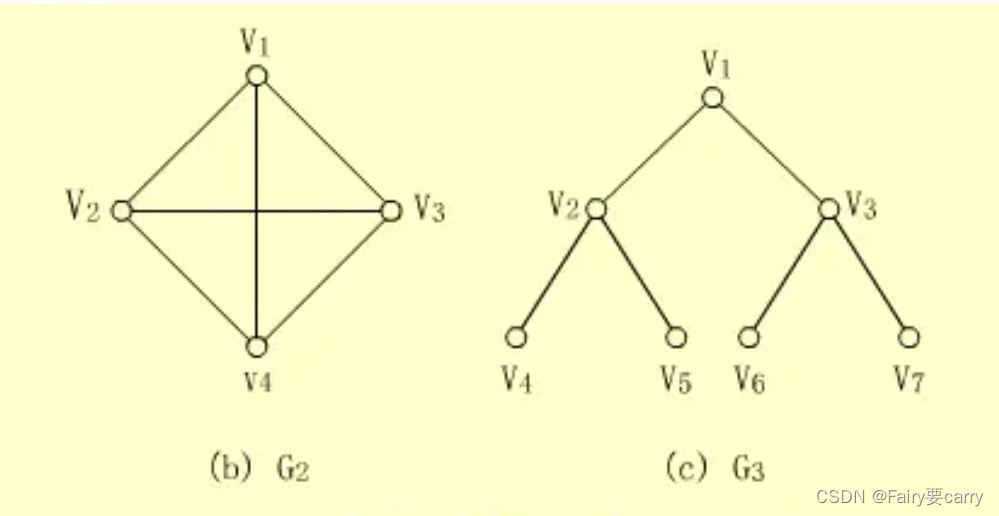
3.区别: n个顶点的完全图有n(n-1)/2条边;而连通图则不一定,但至少有n-1条边。举个例子,四个顶点的完全图有6条边,也就是四条边加上2条对角线;而连通图可以只包含周围四条边就可以了。
4.强连通图:
你到我有路径,我到你有路径——>最少边数为n(环),至多边数为n(n-1);
有向图G中,如果两个顶点vi,vj间(vi>vj)有一条从vi到vj的有向路径,同时还有一条从vj到vi的有向路径,则称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通,称G是一个强连通图。
5.连通分量:
- 子图相通
- 子图极大
与连通图对应,一般书上说的都是特指无向图!!
首先要知道分量,分量其实就是子图,只不过说的高大尚罢了。但连通分量不是简单的子图连通,他还除了要求子图连通,还要求该连通子图极大。说白了,无向图极大连通子图就是连通分量。到这里先往下看极大连通子图再回来看

6.极大连通分量:
从5我们知道他首先是连通子图,并且该连通子图是极大的,主要是这里的极大很不好理解。这里我画图举例

7.极小连通分量:

7.生成树:
连通图的生成树是包含图中全部顶点的一个极小连通子图。

8.生成森林:
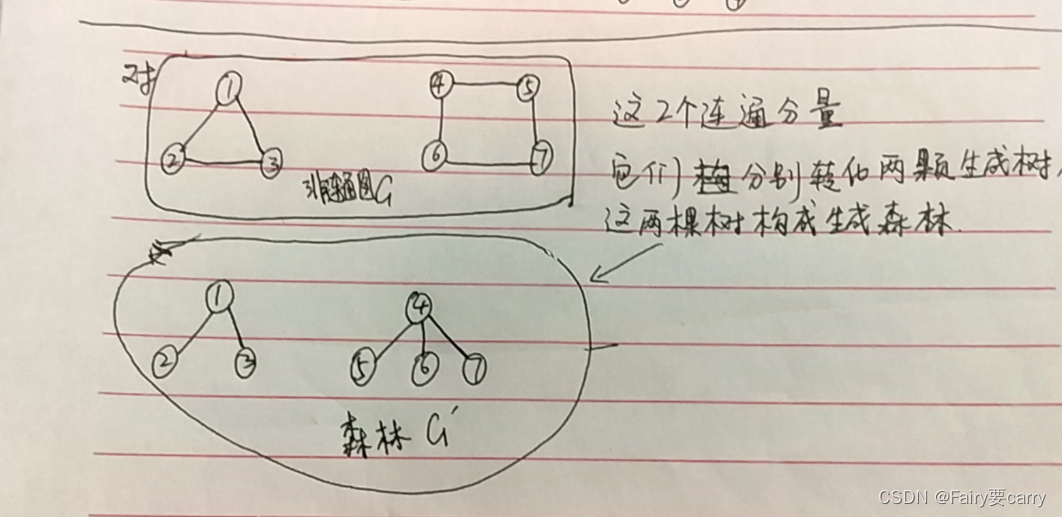
9.有向树
一个顶点的入度为0,其余顶点入度为1的有向图为有向树
例题
1.

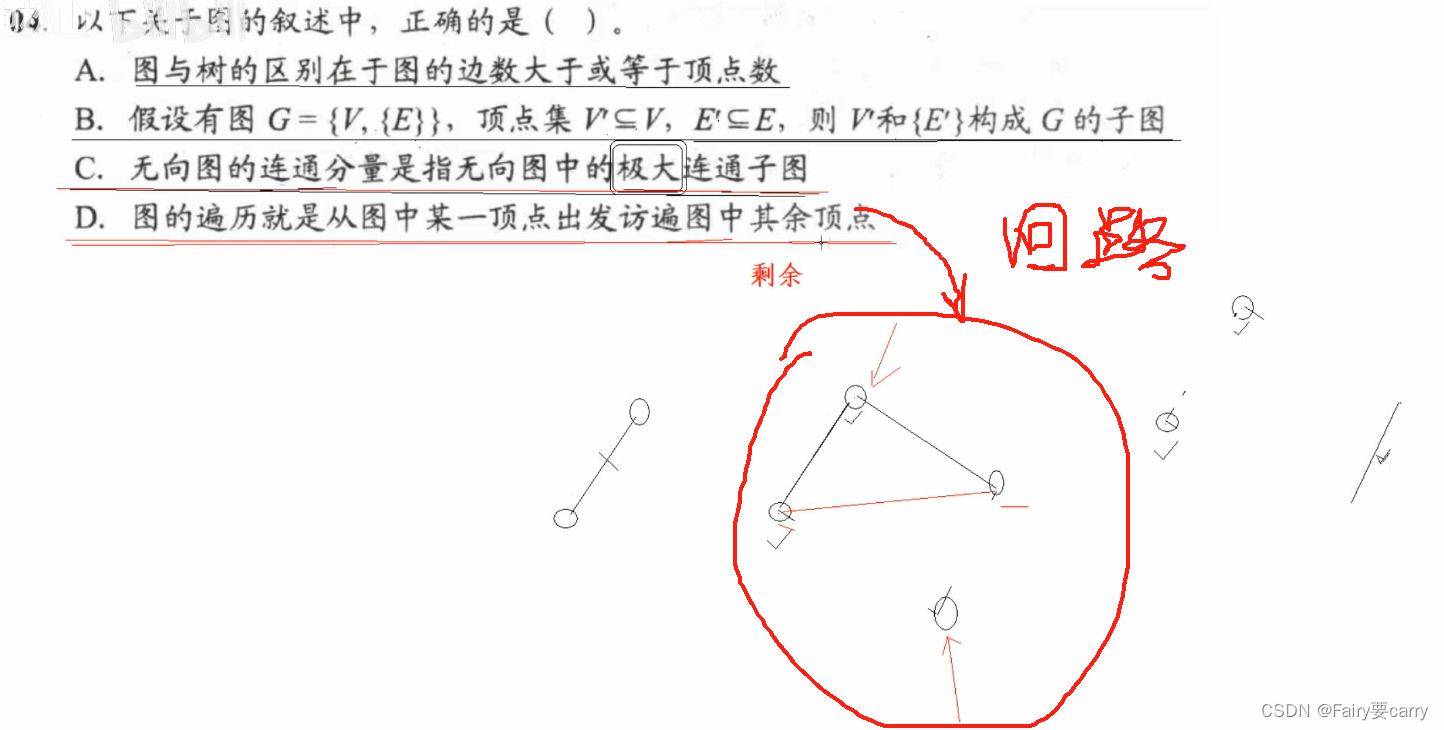
2.
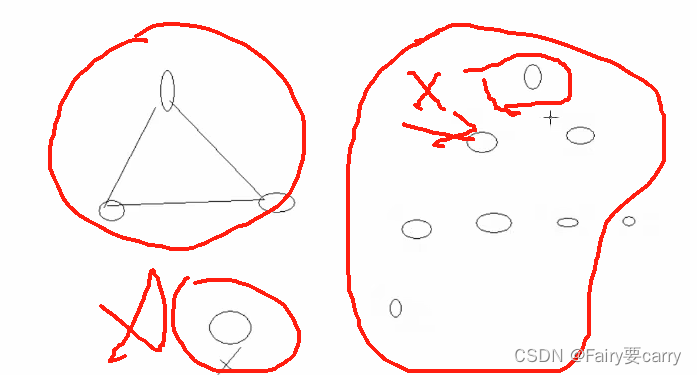
答案选B:
无向图:是没有方向的,而强连通图 强调的是有方向的图
而有回路,也不一定正确,可能会出现以下情况:访问不到其余节点
而一棵树,只有从根节点出发才能访问所有节点

3.
1.子图的概念:
**子图:**假设有两个图G=(V,{E})和g=(v,{e}),如果v⊆V,e⊆E,则称g为G的子图;
例:假设有图G=(V,{E}),顶点集A⊆V,B⊆E,则A和{B}构成G的子图。答:错误,因为A和B未必能构成图。定义中g是G的子图,是因为给条件时已经明确g是图
2.无向完全图和有向完全图的概念:
无向完全图:每个节点之间都有边,为1/2(n(n-1));
有向完全图:任意两个顶点之间都存在方向相反的两条弧。n(n-1);
3.
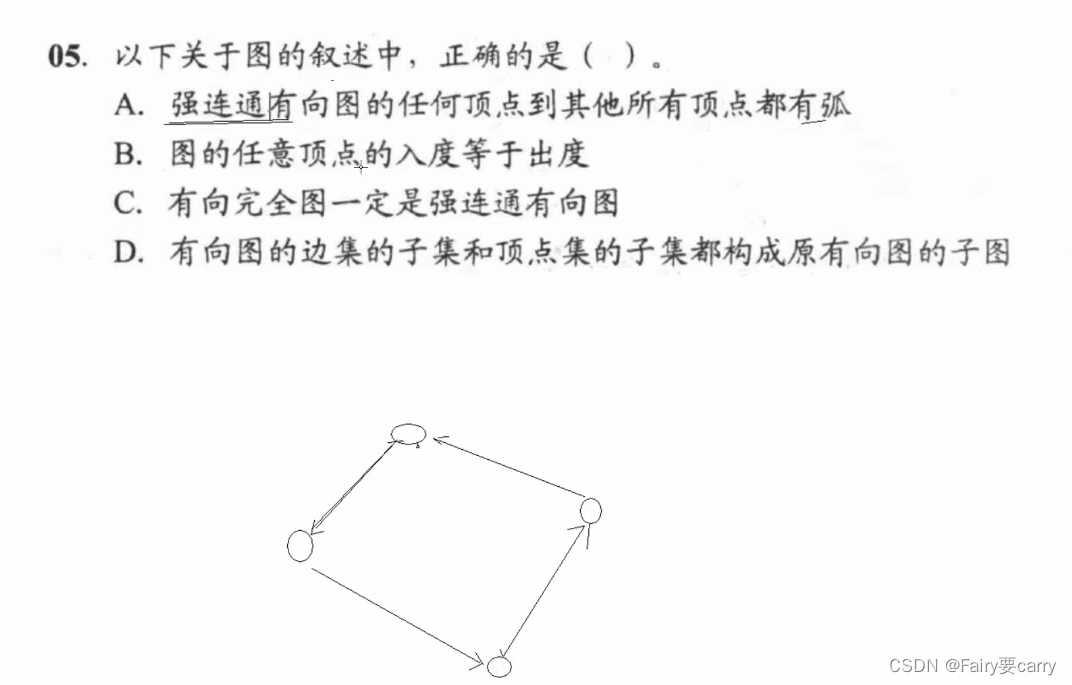
强连通图的概念:
有方向,有边,但是强连通图不能保证任何顶点到其他所有顶点都有弧,可能只与其中之一之间有弧
图的入度和出度:
图的入度和出度不一定相等,入读可能为0
有向完全图:
有边且方向为双向,边数为n(n-1),故有向完全图一定为强连通图 (有边有方向)
有向图边集的子集和顶点的子集不一定能够构成子图:除非明确给出这个子集构成了个图
5.
注意非连通的情况

6.
对于强连通有向图,成一个环,三个节点三条边
你到我有路径,我到你有路径——>最少边数为n(环),至多边数为n(n-1);

7.
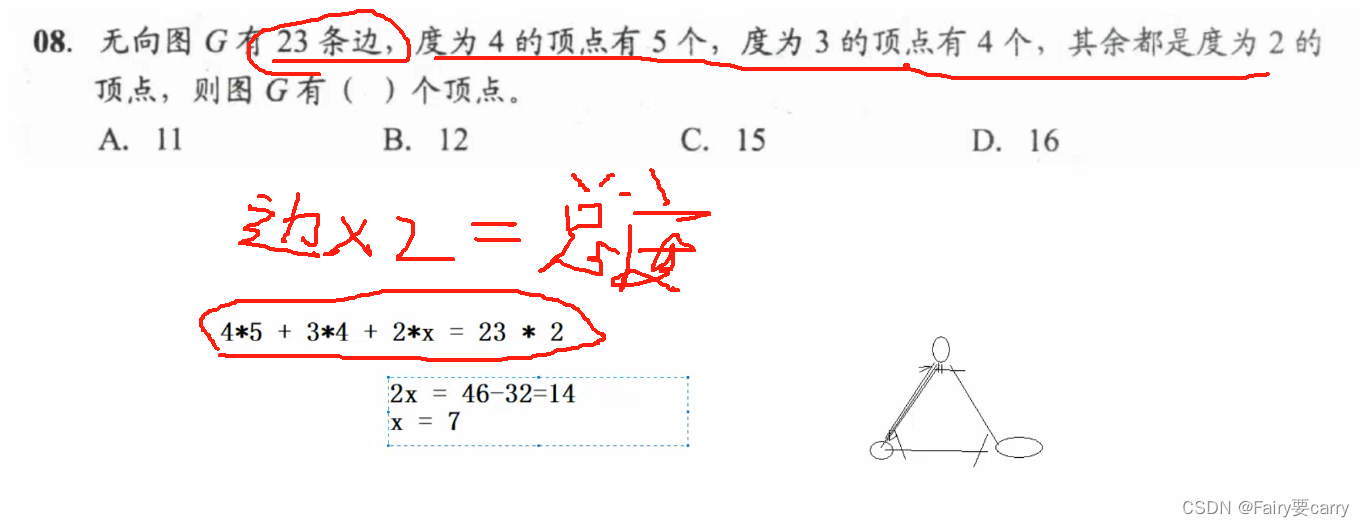
8.
n个顶点最多n-1条边,算入度出度,2*(n-1)

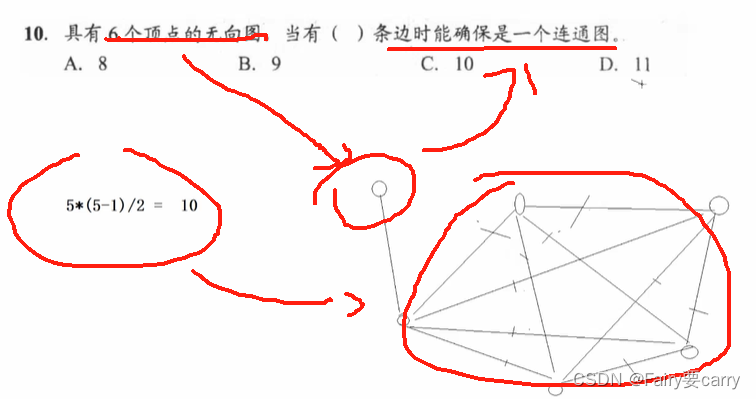
10.
在五个顶点的完全图基础之上再加一个顶点使其为连通图
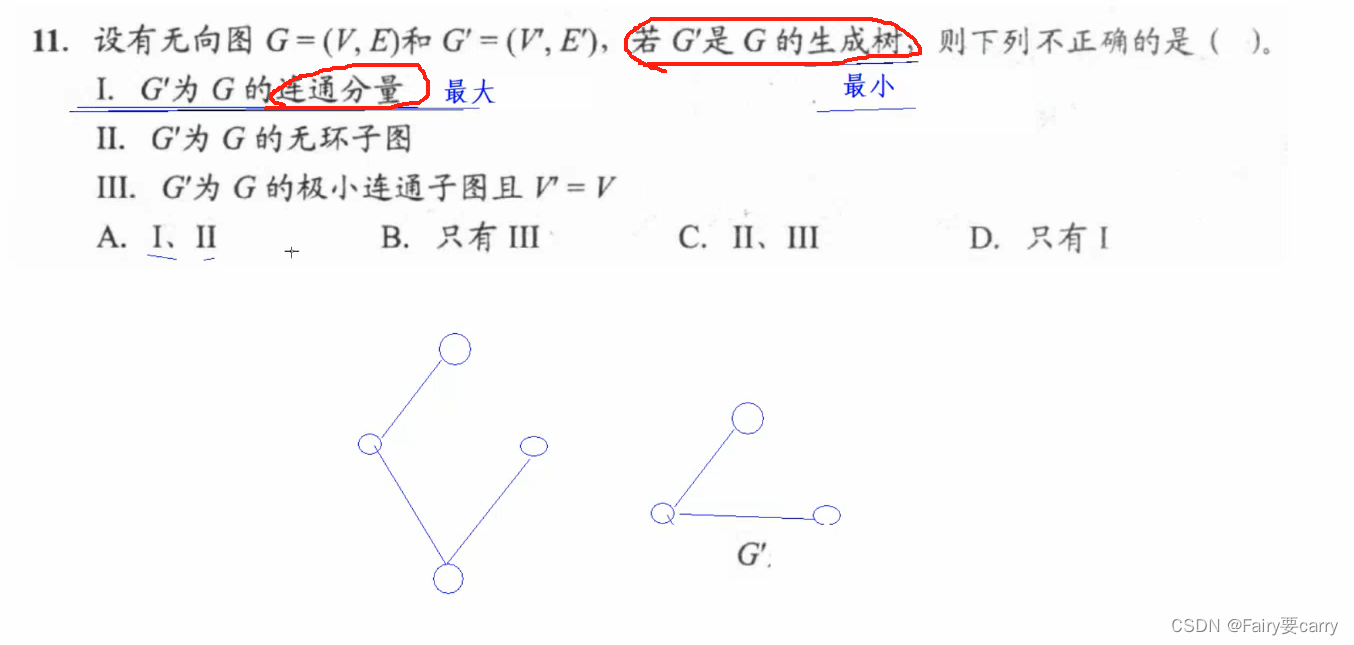
11.
可以知道的是树一定是一个连通图——>所以符合n个节点n-1条边
- 生成树指的是最小连通子树,而连通分量指的是极大连通子树
- 生成树确实是无环的
- 生成树与最下连通子树相关
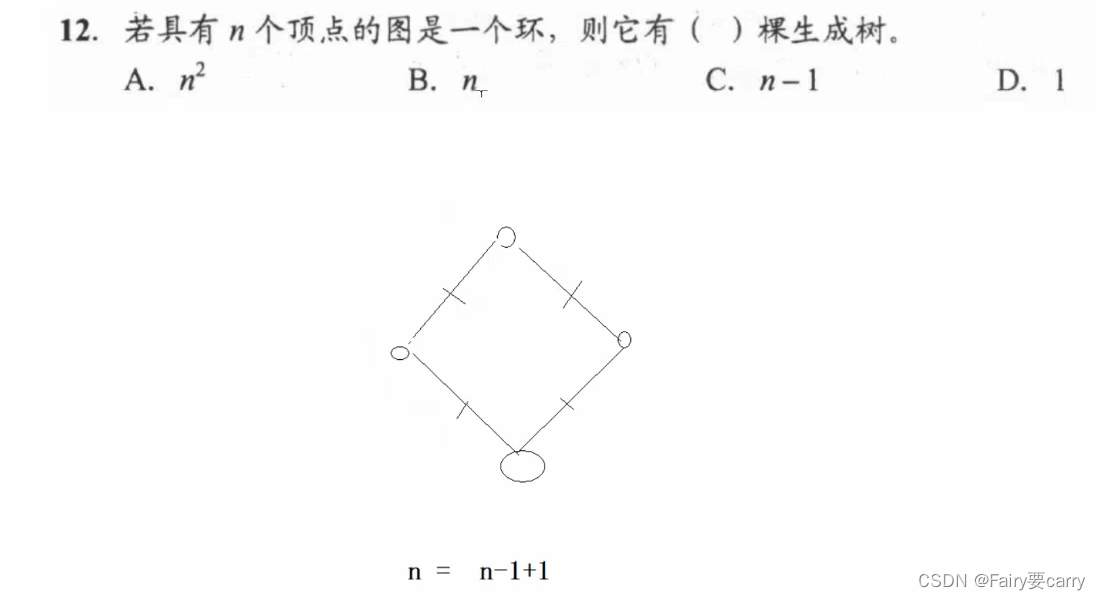
12.
n个顶点,成为一个环,有n个边,n个边有n颗生成树(也可以从度方面思考)
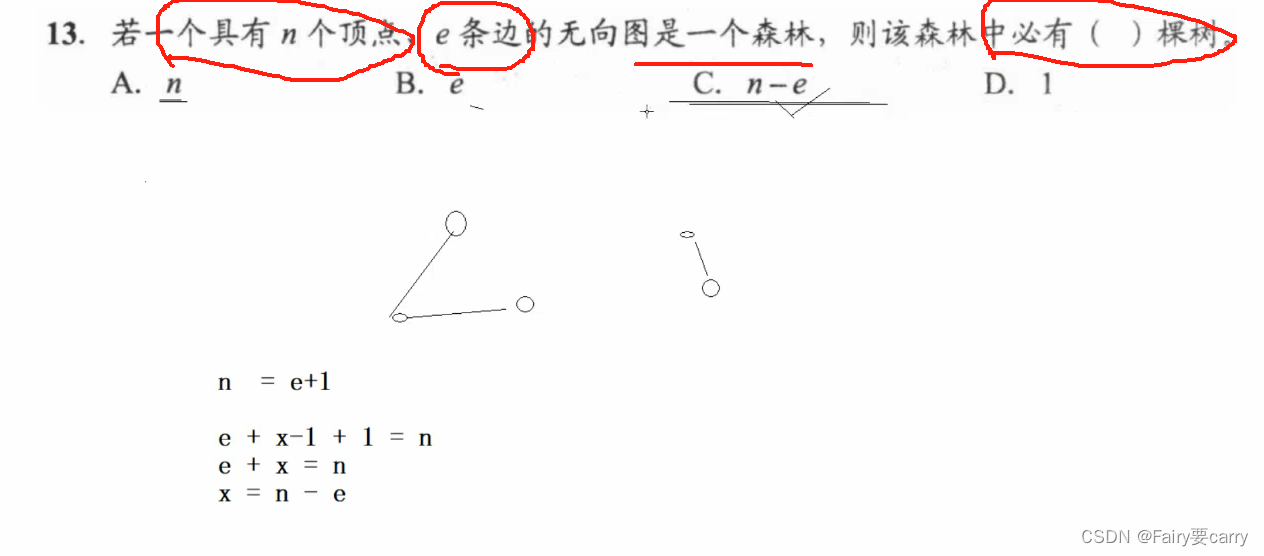
13.
设森林中有s棵树,再用n-1条边就能把所有的树连接成一棵树,此时,边数+1=顶点数,即e+(x-1)+1=n => x=n-e
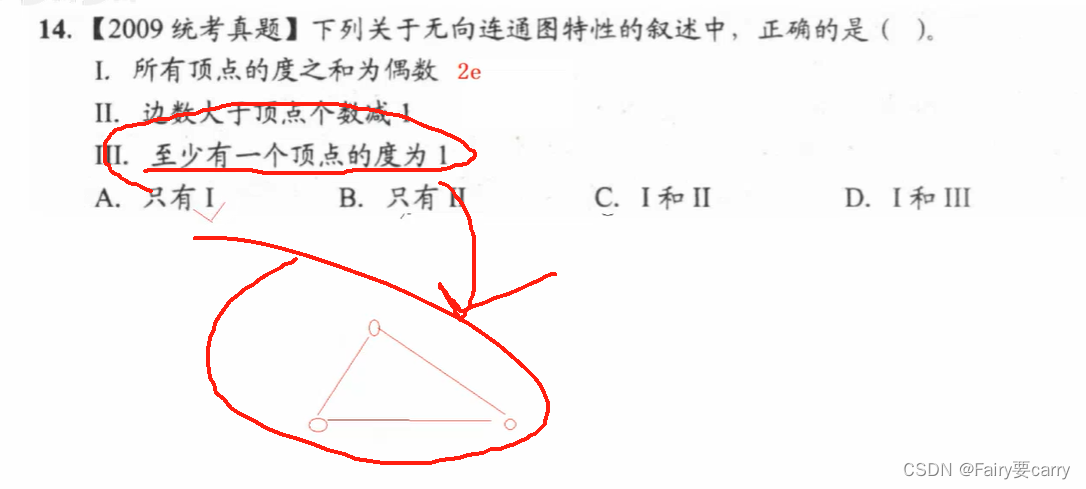
14.
在有向图中,顶点的度为入度与出度之和。n个顶点的有向图中,任一顶点最多还可以与其他n—1个顶点有一对边相连。 2(n-1)*
15.
若图为环,则度最少为2
16.
与上述类似,一个无向图若要有七个节点,要保证它是连通的,说明六个节点的时候是完全图,所以边数为6*(5)/2,但因为要将其变为连通图,所以需要+1条边

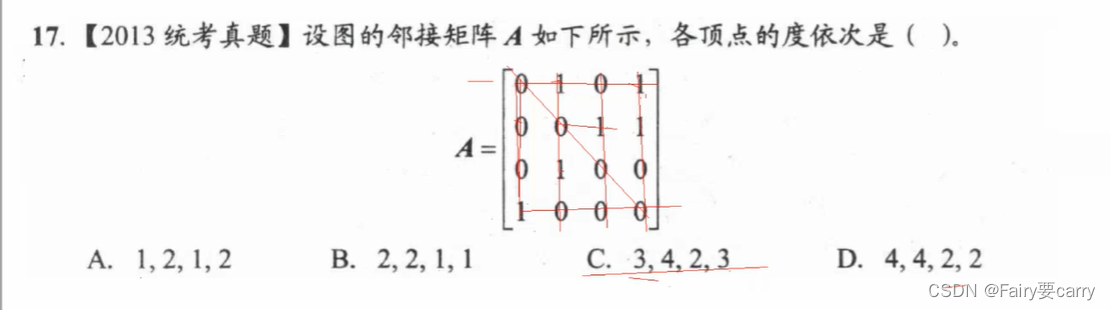
17.邻接矩阵:
非对称的邻接矩阵,说明为有向图,(因为无向图一定是对称的),各顶点的度依次是=入度+出度,为3423
如果是无向图,就要/2;
2.图的存储
邻接矩阵
无向图的邻接矩阵是唯一的;邻接表是唯一的
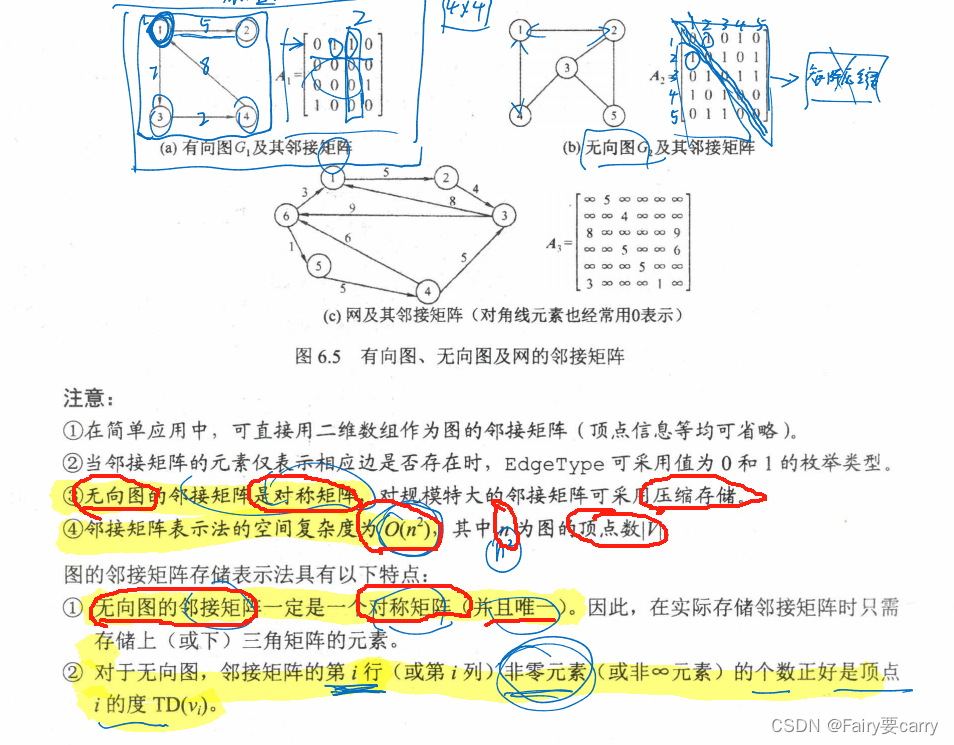
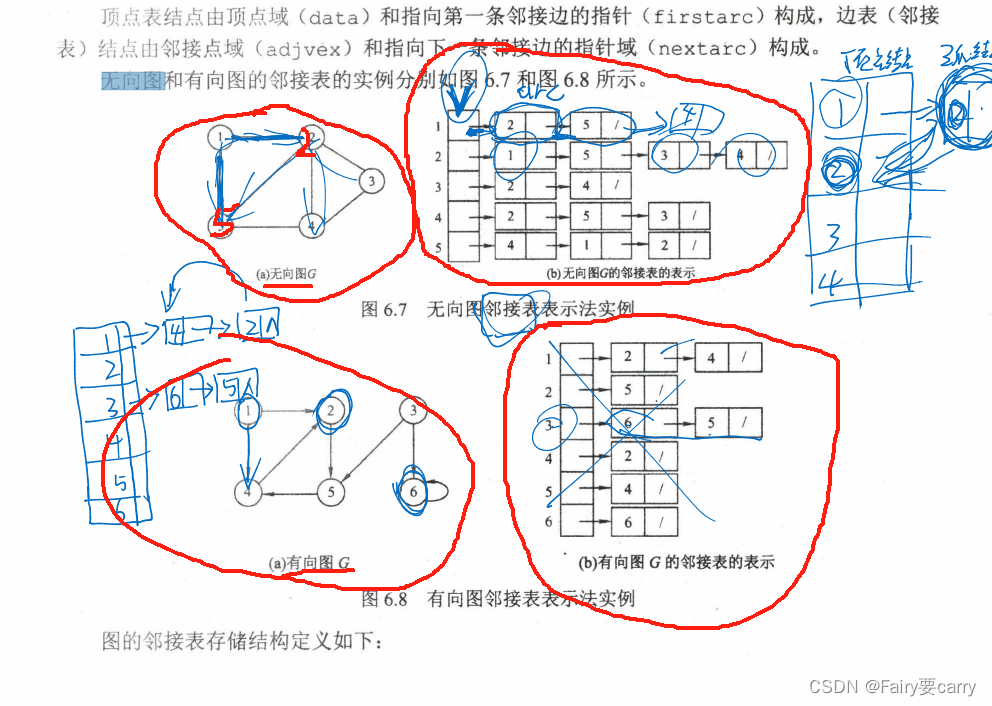
邻接表
**前提:**因为邻接矩阵较为稀疏,所以我们用邻接表法减少空间的消耗
-
有向图,无向图都能够存储
-
邻接表存储有向图时,顶点的出度个数为单链表中的节点个数
-
无向图中,邻接表不唯一,若无向图中有n个顶点、e条边,则其邻接表需要n个头结点和2e个表结点。适宜存储稀疏图。
-

-
无向图和有向图存储空间的比较
**无向图:**顶点数+2*边数;**有向图:**定点数+边数

图的遍历
深度优先DFS:
从上至下遍历,如果到顶了(已经走过的路就不走了),就返回上一步节点
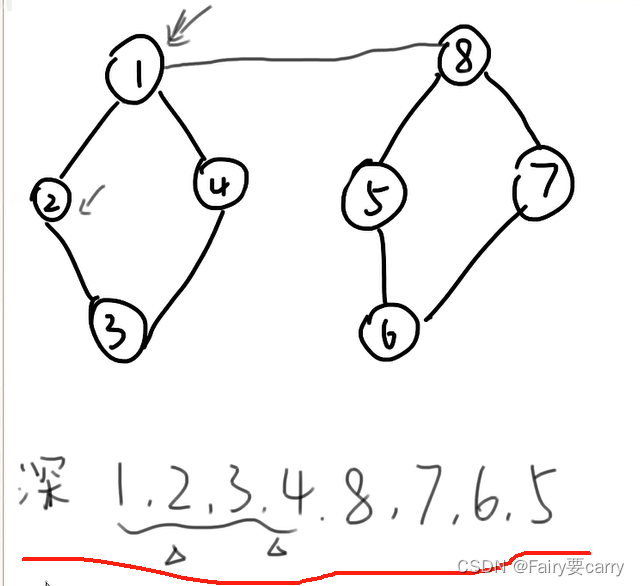
广度优先BFS:
从左到右一层一层遍历,放入(找当前节点距离为1的节点们,放入,然后继续遍历)
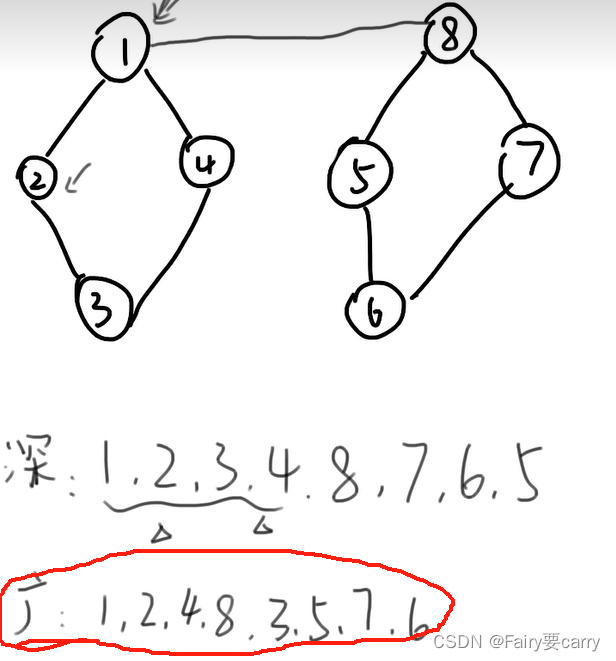
邻接矩阵的遍历:
注意遍历的唯一性
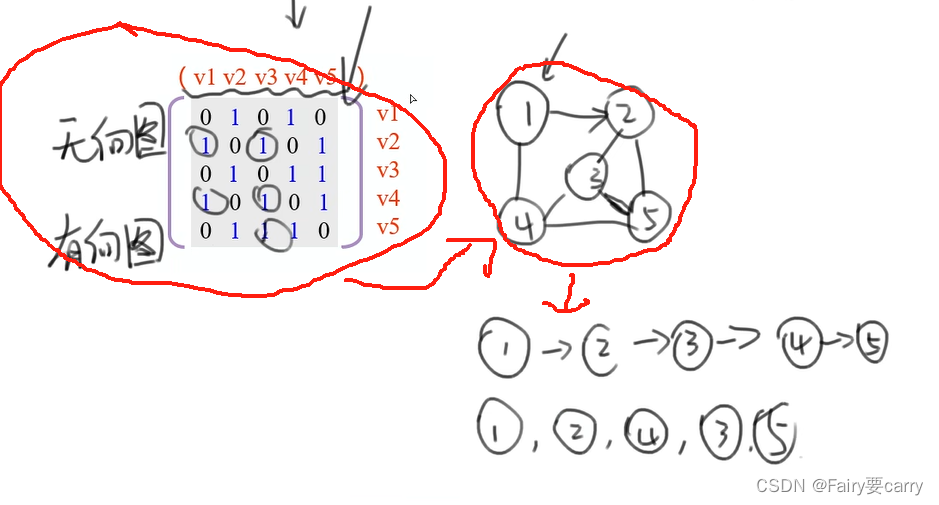
例题
相关文章:

图论例题解析
1.图论基础概念 概念 (注意连通非连通情况,1节点) 无向图: 度是边的两倍(没有入度和出度的概念) 1.完全图: 假设一个图有n个节点,那么任意两个节点都有边则为完全图 2.连通图&…...

图解 TCP 拥塞控制
文章目录 什么是拥塞控制拥塞控制算法慢启动拥塞避免快速恢复 TCP拥塞控制状态机 什么是拥塞控制 拥塞控制是一种 确保网络中的数据包以可持续的速率传输 的机制,避免因为数据包太多而超过网络当前的承载能力,导致网络性能下降,甚至产生大量…...
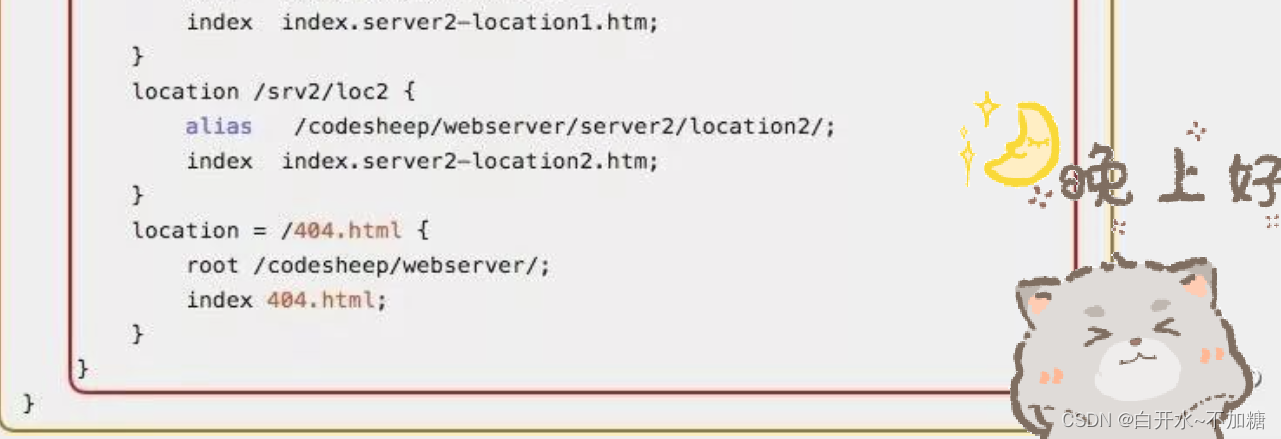
Nginx配置文件的整体结构
一、Nginx配置文件的整体结构 从图中可以看出主要包含以下几大部分内容: 1. 全局块 该部分配置主要影响Nginx全局,通常包括下面几个部分: 配置运行Nginx服务器用户(组) worker process数 Nginx进程PID存放路径 错误…...
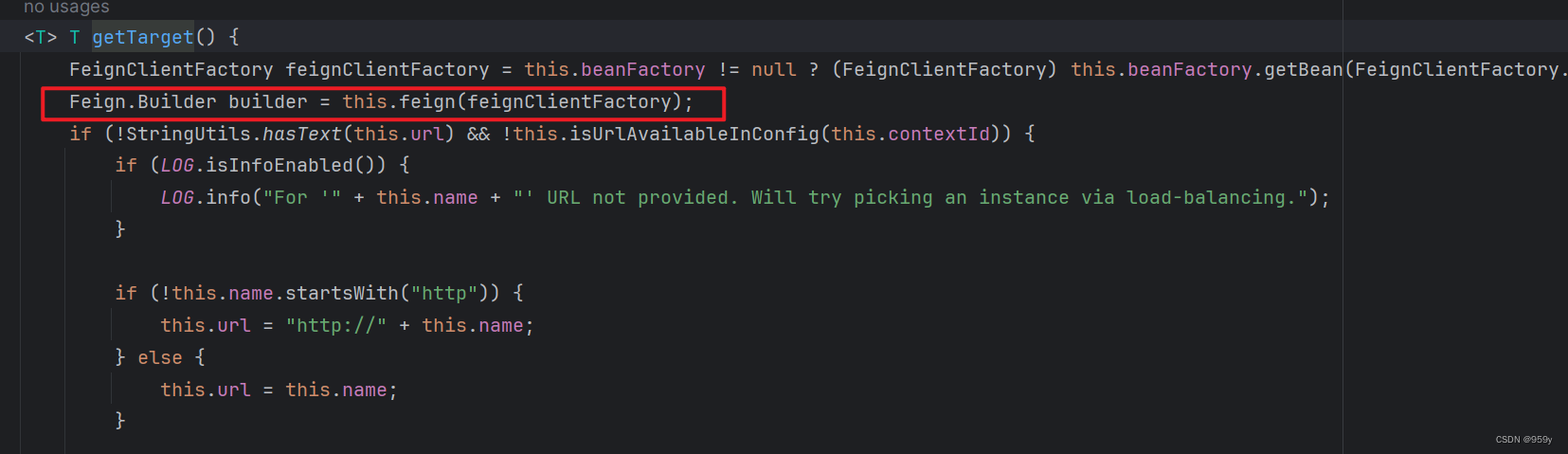
[SpringCloud] OpenFeign核心架构原理 (三)
文章目录 1.SpringCloud是如何整合Feign的1.1 将FeignClient接口注册到Spring中1.2 FeignClientFactoryBean相关 1.SpringCloud是如何整合Feign的 核心组件重新实现, 支持更多的SpringCloud生态的功能。将接口动态代理对象注入到Spring容器中。 1.1 将FeignClient接口注册到S…...

elementUI Table组件点击取当前行索引
在使用element UI Table组件时,需要点击取当前行索引,并删除当前行,看了element UI 文档好象没有这个的,仔细看下发现当前行索引是在scope里的$.index里。 element UI文档:https://www.uihtm.com/element/#/zh-CN/comp…...

组基轨迹建模 GBTM的介绍与实现(Stata 或 R)
基本介绍 组基轨迹建模(Group-Based Trajectory Modeling,GBTM)(旧名称:Semiparametric mixture model) 历史:由DANIELS.NAGIN提出,发表文献《Analyzing Developmental Trajectori…...

解决前端性能问题:如何优化大量数据渲染和复杂交互?
✨✨祝屏幕前的小伙伴们每天都有好运相伴左右,一定要天天开心!✨✨ 🎈🎈作者主页: 喔的嘛呀🎈🎈 目录 引言 一、分页加载数据 二、虚拟滚动 三、懒加载 四、数据缓存 五、减少重绘和回流 …...

【Vue3】深入理解Vue中的ref属性
💗💗💗欢迎来到我的博客,你将找到有关如何使用技术解决问题的文章,也会找到某个技术的学习路线。无论你是何种职业,我都希望我的博客对你有所帮助。最后不要忘记订阅我的博客以获取最新文章,也欢…...

CentOS上安装与配置Nginx
CentOS上安装与配置Nginx Nginx是一款轻量级的Web服务器/反向代理服务器及电子邮件(IMAP/POP3)代理服务器,并在一个BSD-like协议下发行。以下是在CentOS系统上安装和配置Nginx的步骤。 🌟 前言 欢迎来到我的小天地,这…...
DataGrip 连接 Centos MySql失败
首先检查Mysql是否运行: systemctl status mysqld , 如果显示没有启动则需要启动mysql 检查防火墙是否打开,是否打开3306的端口 sudo firewall-cmd --list-all 如果下面3306没有打开则打开3306端口 publictarget: defaulticmp-block-inver…...
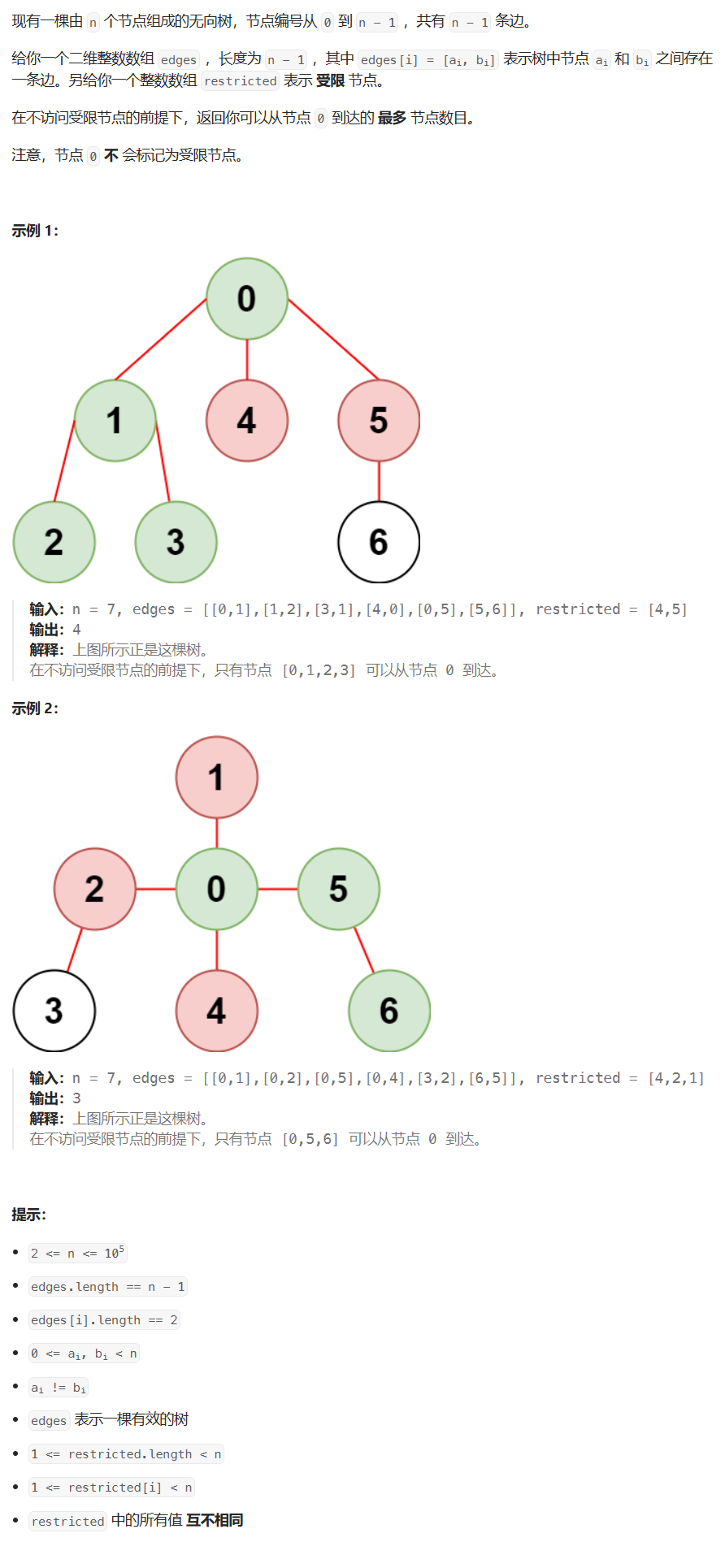
【图论】图的遍历 - 构建领接表(无向图)
文章目录 例题:受限条件下可到达节点的数目题目描述代码与注释模板抽象 例题:受限条件下可到达节点的数目 题目链接:2368. 受限条件下可到达节点的数目 题目描述 代码与注释 func reachableNodes(n int, edges [][]int, restricted []int)…...

Claude 3家族惊艳亮相:AI领域掀起新浪潮,GPT-4面临强劲挑战
🌈个人主页: Aileen_0v0 🔥热门专栏: 华为鸿蒙系统学习|计算机网络|数据结构与算法|MySQL| 💫个人格言:“没有罗马,那就自己创造罗马~” #mermaid-svg-agd7RSCGMblYxo85 {font-family:"trebuchet ms",verdana,arial,sans-serif;f…...

Linux Watchdog 机制是什么
当涉及到Linux操作系统的稳定性和可靠性时,Linux Watchdog机制是一个至关重要的议题。该机制旨在监控系统状态,确保在出现问题时采取适当的措施以维持系统的正常运行。本文将深入探讨Linux Watchdog机制的工作原理、应用范围以及如何配置和使用该机制来提…...

Linux权限问题
1.用户 Linux系统下分为两种用户 a.超级用户(root) b.普通用户 超级用户的命令提示符是“#”,普通用户的命令提示符是“$” 怎么切换用户呢? 命令 su 用户名 其中切换root可以为su 或者su root-----不用密码 普通用户切换…...

python基础练习题目
1. 根据身高体重,判断人的胖瘦 描述: 通过身高和体重,判断一个人的胖瘦。国际上一般采用BMI体重指数,计算公式为BMI 体重 / 身高2(保留小数点后1位),参考标准如下:…...

视频编码标准H.264/AVC,H.265/HEVC,VP8/VP9,AV1的基本原理、优缺点以及适用场景
视频编码标准是用于压缩数字视频数据的技术规范,以减少存储和传输所需的带宽。以下是关于H.264/AVC、H.265/HEVC、VP8/VP9和AV1这些标准的基本原理、优缺点以及适用场景的简要描述: H.264/AVC (Advanced Video Coding) 基本原理: H.264是一…...
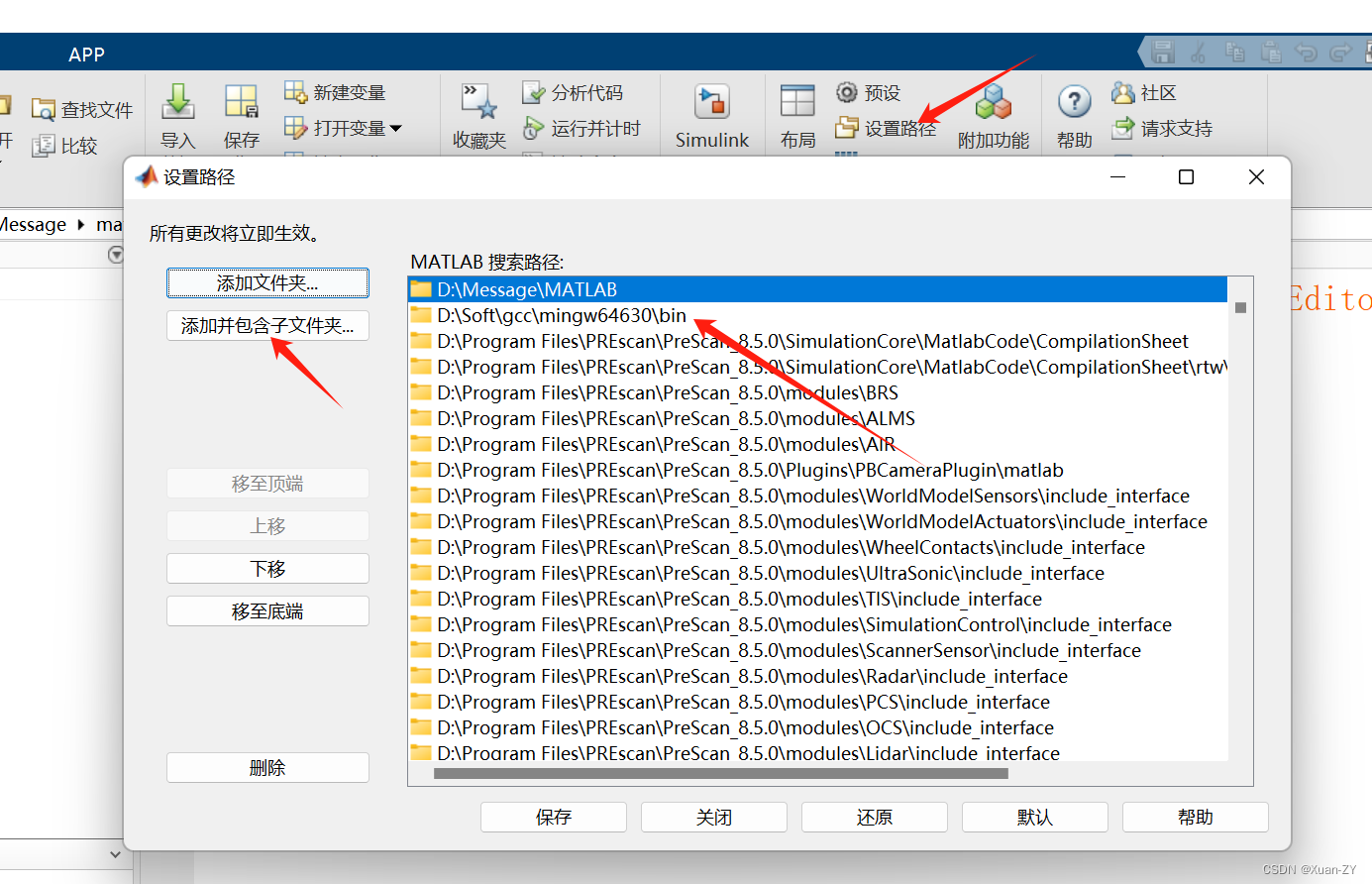
MATLAB2020a安装编译器mingw-64(6.3.0)
MATLAB2020a指定安装mingw-64(6.3.0)版本编译器 记录一下几个要点 mingw-64(6.3.0) 找到对应的mingw-64安装包 设置mingw的bin文件路径到环境变量 变量名:MW_MINGW64_LOC MATLAB设置路径...

Python网络请求高级篇:Requests库的深度运用
在Python网络请求中级篇中,我们了解了如何通过Requests库发送带参数的请求,处理Cookies,使用Session对象,以及设置请求头。在本文中,我们将进一步深入学习Requests库的高级功能,包括处理重定向,…...

AWS认证
AWS新增DEA-C01认证考试知识要点 原创 云计算狂魔 云计算狂魔 2024-03-04 23:58 北京 由于AWS将于3月12日正式启动DEA-C01认证考试,我们整理了相关考试知识要点,请各位考生了解。...
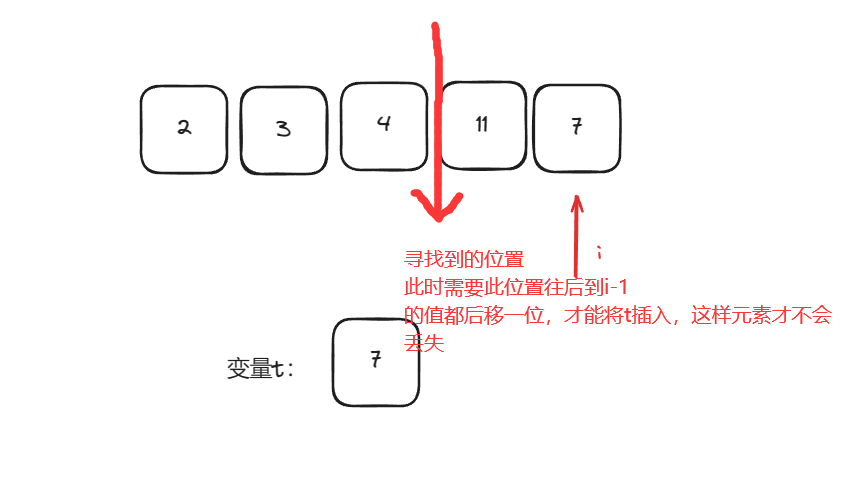
【排序】详解插入排序
一、思想 插入排序是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。具体步骤如下,将数组下标为0的元素视为已经排序的部分,从1开始遍历数组,在遍历的过程中当前元素从…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...
与文本切分器(Splitter)详解《二》)
LangChain 中的文档加载器(Loader)与文本切分器(Splitter)详解《二》
🧠 LangChain 中 TextSplitter 的使用详解:从基础到进阶(附代码) 一、前言 在处理大规模文本数据时,特别是在构建知识库或进行大模型训练与推理时,文本切分(Text Splitting) 是一个…...

Vue 3 + WebSocket 实战:公司通知实时推送功能详解
📢 Vue 3 WebSocket 实战:公司通知实时推送功能详解 📌 收藏 点赞 关注,项目中要用到推送功能时就不怕找不到了! 实时通知是企业系统中常见的功能,比如:管理员发布通知后,所有用户…...
