蓝桥杯备赛 day2 | 4. 付账问题 5. 数字三角形
付账问题,关键是要了解整型的范围,确定获取输入数据的变量类型

 需要注意的是int的十进制范围
需要注意的是int的十进制范围-32768 ~ 32767,那么我们可以知道,人数n是可以用int来装的,需付款数S应该是long long,获取的每个人初始钱数也应该是long long
同时,由于最终结果才要求用小数,在中间计算里尽量不要出现除法(如果可以的话),避免除法丢失精度
#include<iostream>
#include<bits/stdc++.h>
using namespace std;
static bool comp(const long long & a,const long long & b){return a < b;
}
int main(){long long n;long long s;cin>>n>>s;vector<long long> money;for(auto i = 0;i< n;i++){long long a;cin>>a;money.push_back(a);}sort(money.begin(),money.end(),comp);double avg = 1.0 * s / n ;double sum = 0.0;for(auto i = 0;i< n;i++){if(money[i] * (n-i) < s){sum+= (money[i] - avg) * (money[i] - avg); s -= money[i];}else{double finalAvg = 1.0 * s / (n-i) ;sum += (finalAvg -avg)*(finalAvg -avg)* (n-i);break;}}printf("%.4lf",sqrt(sum / n));return 0;
}
不过这道题很奇怪,判题系统在我使用变量S的时候判错,把变量S改为小写的s就正确了;double avg = 1.0 * s / n ;这种语句,1.0在后面乘也是错的,改个顺序又没事了,没搞懂。。。


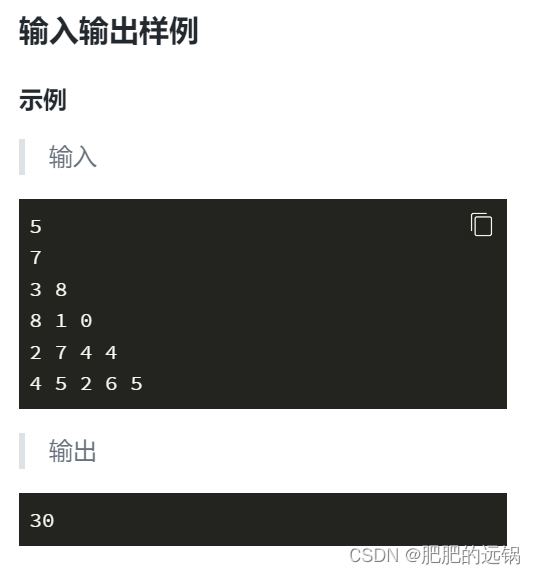
这道题一开始想着数据量小,直接回溯法,没想到这都能超时,只能从回溯递归的暴力解改回动态规划了(不过我这个不是很熟,可以大概讲讲暴力->dp的修改思路)
首先,暴力回溯是有可能不断走前几轮已经走过的路径的,如果强行算下去实际的时间复杂度O(n!)很大,无法接受。这个时候使用dp,其实就是把已经经历过的状态都记录下来,当再次经历这个状态时,就从dp的状态表里获取已有的数据,这样相当于把计算量大大削减,时间复杂度甚至可以到O(n)
想要把算法实现从暴力回溯改到dp,实际上就是从自顶向下的递归改到自底向上的递推,或是从自底向上的递归改到自顶向下的递推。我们首先要找出递归算法中原问题和子问题的自变量是啥,也就是状态,比如dfs里面的自变量就是横纵坐标i和j,然后实际的结果是啥(这个一般就是题目要你求的解,也是你递归函数最后在返回时要得到的东西),那么dp状态表我们就可以知道了,有一个状态,dp状态表就是一维的,两个就是二维,dp[i][j]表示i和j状态变化可以得到的某某结果
然后在dp状态表里填入base case,这就是看是从自顶向下的递归改到自底向上的递推,或是从自底向上的递归改到自顶向下的递推,前者的base case就在后面(因为要改成自底向上的递推),后者就是在前面因为要改成自顶向下的递推)
状态转移方程就看你的递归函数的实现,其实就是递归的逆过程,递归的各个状态咋倒回来
可以看看我这道题的解法,一开始是用的dfs递归,后续写了一个逆过程递推函数traceback,体会一下
#include<bits/stdc++.h>
#include<iostream>
using namespace std;vector<vector<int>> matrix;
vector<vector<int>> dp;
vector<int> nextVec;
int res = INT_MIN;
void resInit(int n){for(int i = 0;i< n;i++){vector<int> vec(n,0);matrix.push_back(vec);dp.push_back(vec);}for(int i = 1;i<= n;i++){for(int j = 0;j< i;j++){cin>>matrix[i-1][j];if(i == n){dp[i-1][j] = matrix[i-1][j]; }}}for(int i = 0;i< 2;i++){nextVec.push_back(i);}}
void traceback(int & n){//base case 在dp初始化时已经做好 -> 第n-1行for(int i = n-2;i>= 0;i--){for(int j = 0;j< n;j++){if(i+1 < n && j+1 < n){dp[i][j] = max(dp[i+1][j] + matrix[i][j],dp[i+1][j+1] + matrix[i][j]);}else if(i+1 < n && j+1 >= n){dp[i][j] = dp[i+1][j] + matrix[i][j];} }}}/*void dfs(vector<int> & chooseList,int sum,int i,int j,int & n){if(i < 0 || i> n-1 ){res = (res < sum) ? sum : res;return; }for(int c : chooseList){dfs(chooseList,sum+matrix[i][j],i+1,j+c,n);}return;
}*/int main(){int n;cin>>n;resInit(n);//dfs(nextVec,0,0,0,n);// printf("%d",res);traceback(n);printf("%d",dp[0][0]);return 0;
}
相关文章:

蓝桥杯备赛 day2 | 4. 付账问题 5. 数字三角形
付账问题,关键是要了解整型的范围,确定获取输入数据的变量类型 需要注意的是int的十进制范围-32768 ~ 32767,那么我们可以知道,人数n是可以用int来装的,需付款数S应该是long long,获取的每个人初始钱数也应…...
2024关于idea激活码报This license xxxx has been suspended
HOSTS文件中增加 0.0.0.0 www.jetbrains.com 0.0.0.0 account.jetbrains.com 然后...
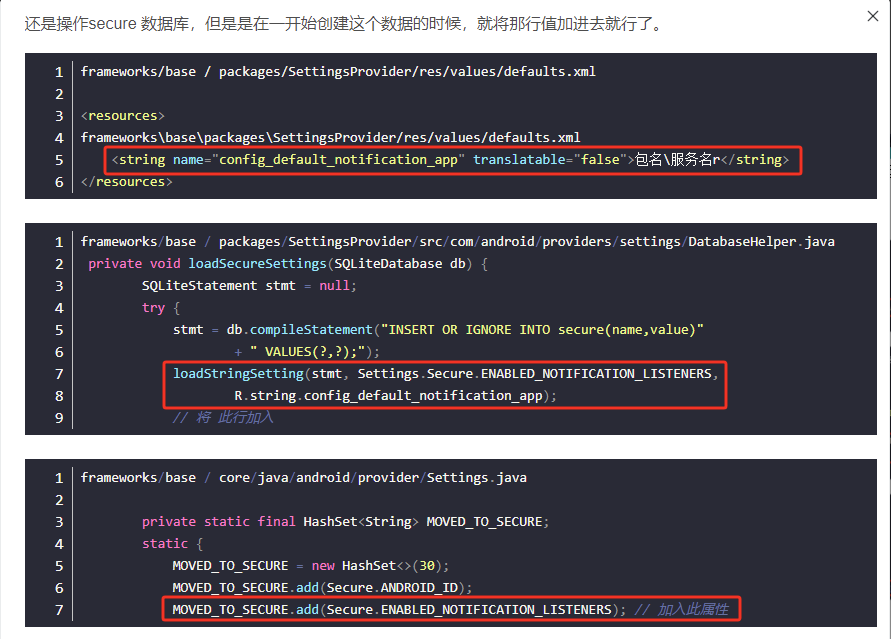
Android9-W517-使用NotificationListenerService监听通知
目录 一、前言 二、前提 三、方案 方案一 方案二 方案三 方案四 方案五 方案六 方案七 四、关于NotificationListenerService类头注释 五、结论 一、前言 NotificationListenerService可以让应用监听所有通知,但是无法获得监听通知的权限,如…...

git的“You can‘t push commits with committe“解决方法
如果使用错误的用户和邮箱执行了git提交,在执行 git push 时将遇到如下错误: ! [remote rejected] feature_116390305_story_0 -> feature_116390305_story_0 (You cant push commits with committer ‘yijian’ or email eyjianqq.com who is not ex…...
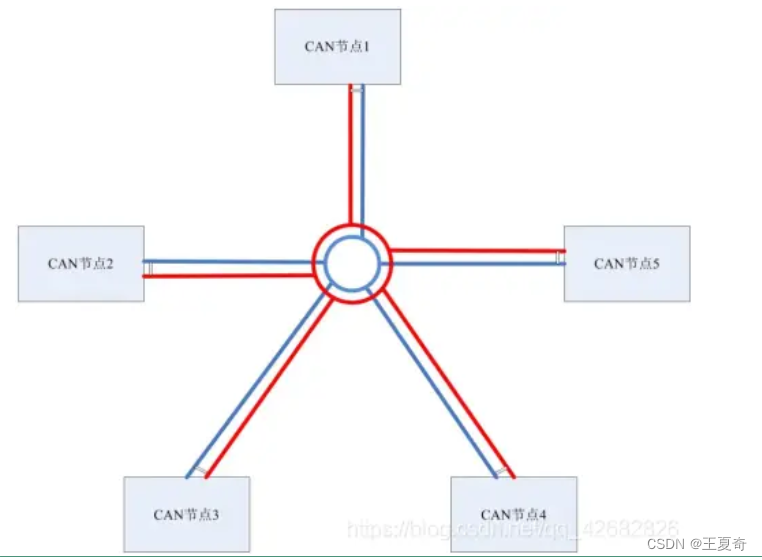
CAN总线的拓扑类型和CAN收发器(原理讲解)
1:CAN收发器(原理讲解) 从原理上来讲CAN_H拉升电压,或CAN_L拉低电压的原理。 以上是TJA1145AT的俯瞰图,此芯片是NXP比较先进的CAN收发器,带SPI总线系统。 回到正题,CAN_H和CAN_L收发器是通过内…...
如何实现WordPress后台显示文章、分类目录、标签等的ID?
我们平时在使用WordPress的过程中,偶尔需要用到文章的ID,或分类目录ID,或标签ID,或媒体库ID,或评论ID,或用户ID等,但是WordPress后台默认是不显示它们的ID的。 今天boke112百科就跟大家分享如何…...
)
【GB28181】SIP协议实践之Windows下VS2019编译eXosip、osip,测试(附工程源码,一键打开编译)
引言 SIP开源库或者GB28181,这里选择了osip和eXosip,但是这两个库的编译使用有些麻烦,源码下来之后编译会出现很多问题,网上也没有找到完整的编译介绍,只能一步一步的找办法解决,以下帮大家整理编译过程。 如果不想编译,可以跳转文章末尾链接直接下载相应工程直接编译即…...

GPT提示语格式——个人自用
总体格式 指令:将 输入 划分为/翻译为/提取出/... 输出 输出格式:... 输入示例:... 输出示例:... 输入:... 输出:基本概述 示例 指令: 提取以下文本中的介词。 输入:“虽然这些发展…...

MCU最小系统电路设计(以STM32F103C8T6为例)
目录 一、何为最小系统? 二、最小系统电路设计 1.电源 (1)各种名词解释 (2)为什么会有VDD_1 _2 _3区分? (3)Mirco USB (4)5v->3.3v滤波电路 &#…...

[JavaWeb学习日记]JSP+Cookie+Filter与登录+CRUD案例
目录 一.JSP 二.EL表达式与JSTL标签 三.Cookie 四.Session 五.Filter 六. 登录CRUD:品牌增删改查案例 Demo一览 1.导包 2.构建包结构 3.创建数据库表tb_brand与user 4.创建实体类 5.mybatis的配置文件和logback配置文件 6.写接口 7.工具类:生成图片与…...

Ruby网络爬虫教程:从入门到精通下载图片
概述 网络爬虫技术在信息时代扮演着重要的角色,它可以自动化地获取互联网上的信息,为用户提供便利的数据服务。本文将带领读者从零开始,通过学习Ruby编程语言,逐步掌握网络爬虫的设计与实现,重点介绍如何利用网络爬虫技…...
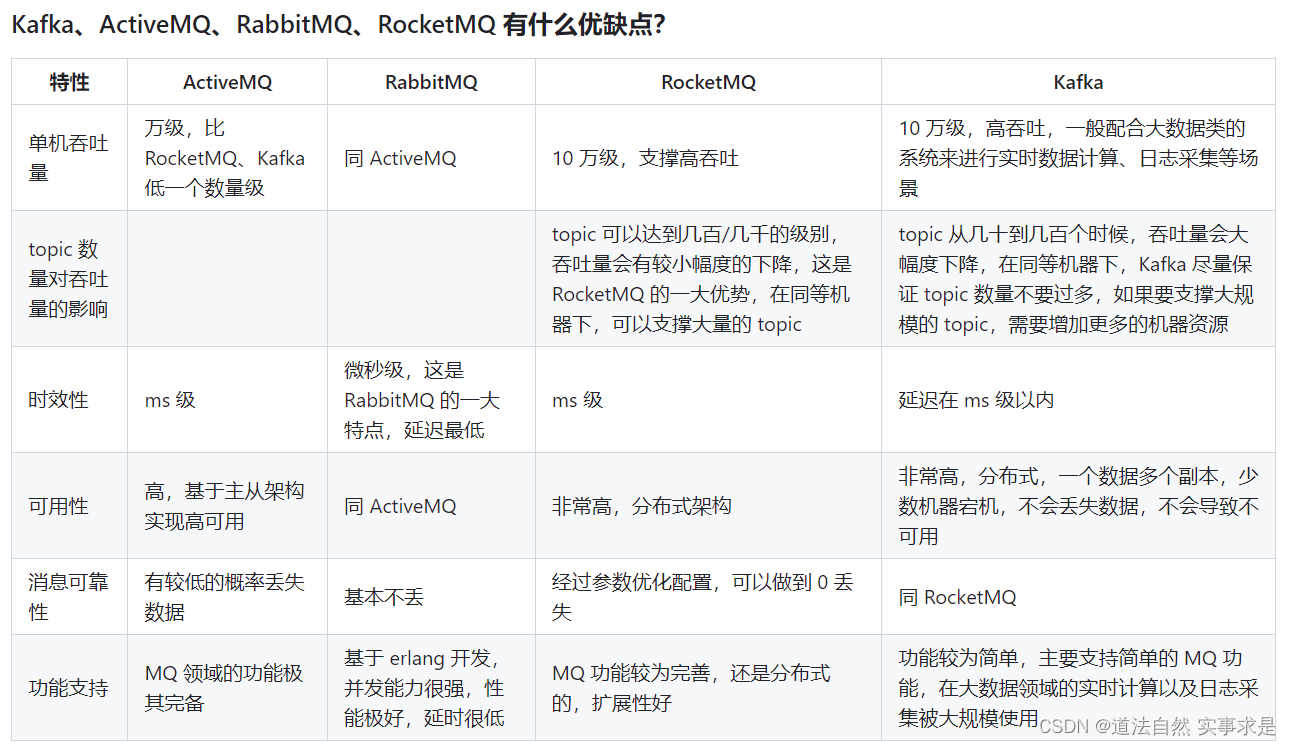
各中间件性能、优缺点对比
参考资料: Kafka、ActiveMQ、RabbitMQ、RocketMQ 有什么优缺点?...

修改表中某个字段等于另一个字段减去 2 小时的 SQL
需求:将表中到达时间按照客户要求改为比赛时间的提前 N 小时,具体如下: 表结构 update contestSchedule SET mainRefereeArrivalTimeDATE_FORMAT(CONCAT(2024-03-04 ,gameTime)- INTERVAL 2 HOUR, %H:%i), assistantRefereeArrivalTimeDAT…...
Jetpack Compose: Hello Android
Jetpack Compose 是一个现代化的工具包,用于使用声明式方法构建原生 Android UI。在本博文中,我们将深入了解一个基本的 “Hello Android” 示例,以帮助您开始使用 Jetpack Compose。我们将探讨所提供代码片段中使用的函数和注解。 入门 在…...
3月3号)
蓝桥每日一题 (差分)3月3号
//3279改变数组元素 自己做TLE:奈何想不出怎么用差分 #include<bits/stdc.h> using namespace std; //3279 改变数组元素(超时) const int N2e510; vector<int>a; int t,n; int main() {cin>>t;while(t--){cin>>n;…...
)
Mybatis和Spring Data Jpa的优缺点比较(八股文)
ORM(Object-Relational Mapping)框架是一种用于实现对象与关系数据库之间映射的工具或库。它可以将数据库中的表和记录映射成对象和属性,使开发人员可以使用面向对象的方式操作数据库,而不需要编写复杂的SQL语句。ORM框架的主要功…...

LeetCode买卖股票的最佳时机
LeetCode买卖股票的最佳时机 121 买卖股票的最佳时机Ⅰ 题目描述 给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。 你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计…...
----->A. Entertainment in MAC)
Codeforces Round 932 (Div. 2)----->A. Entertainment in MAC
一,思路: 简单的字符串处理,当反转字符串后如果字典序减小了,那么肯定不会再执行反转操作,而是执行操作2,将反转后的字符串拼接(这样必定构造一个回文串),那么之后的操作…...

【JavaScript】 短路运算的妙用 ||
短路运算的妙用 下方举例中的写法技巧,在实际开发中,经常用到。这种写法,是一种很好的「容错、容灾、降级」方案,需要多看几遍。 1、JS 中的&&属于短路的与: 如果第一个值为 false,则不会执行后面的…...

密码学之椭圆曲线
引言 DH(Diffie-Hellman)密钥交换算法于1976年提出,是第一个公开密钥交换算法。其基础是数学中的群论,群论也是大多数公开密钥密码的基础。简单来说,群是一组元素的集合以及在这些元素上定义的特殊二元运算。 一个群需要满足如下性质: 封闭性:群中两个元素的运算结果仍…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...

人工智能--安全大模型训练计划:基于Fine-tuning + LLM Agent
安全大模型训练计划:基于Fine-tuning LLM Agent 1. 构建高质量安全数据集 目标:为安全大模型创建高质量、去偏、符合伦理的训练数据集,涵盖安全相关任务(如有害内容检测、隐私保护、道德推理等)。 1.1 数据收集 描…...

Android写一个捕获全局异常的工具类
项目开发和实际运行过程中难免会遇到异常发生,系统提供了一个可以捕获全局异常的工具Uncaughtexceptionhandler,它是Thread的子类(就是package java.lang;里线程的Thread)。本文将利用它将设备信息、报错信息以及错误的发生时间都…...

C# winform教程(二)----checkbox
一、作用 提供一个用户选择或者不选的状态,这是一个可以多选的控件。 二、属性 其实功能大差不差,除了特殊的几个外,与button基本相同,所有说几个独有的 checkbox属性 名称内容含义appearance控件外观可以变成按钮形状checkali…...
