数电学习笔记——逻辑函数及其描述方法
目录
一、逻辑函数
二、逻辑函数的描述方法
1、逻辑真值表
2、逻辑函数式
3、逻辑图
4、波形图
三、逻辑函数的两种标准形式
1、最小项与最大项
最小项
最小项的性质
最大项
最大项的性质
2、最大项与最小项的关系
3、逻辑函数的最小项之和形式
4、逻辑函数的最大项之和形式
一、逻辑函数
以逻辑变量作为输入,以运算结果作为输出,那么当输入确定时,输出也就确定下来了。这是一种函数关系,称为逻辑函数,其写作Y=F(A,B,C,...)
由于该函数的输入与输出只有0/1两种状态,所以它是二值逻辑函数。
二、逻辑函数的描述方法
1、逻辑真值表
此方法不作赘述,在之前的文章已经提到多次。
2、逻辑函数式
将输入与输出之间的逻辑关系式写成与、或、非等运算的组合式,即逻辑代数式,也就得到了逻辑函数式。
例如:Y=A(B+C)
3、逻辑图
将逻辑函数式中各变量之间的与、或、非等逻辑关系用图形符号表示出来,就可以画出描述函数关系的逻辑图。
例如: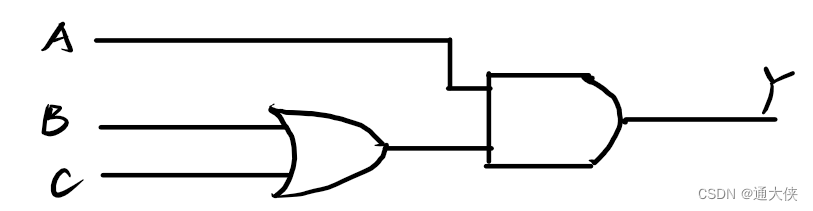
图2.1 逻辑图
4、波形图
如果将逻辑函数输入变量每一种可能出现的取值与对应的输出值按时间顺序依次排序起来,就得到了描述该逻辑函数的波形图,也称时序图。
图2.2 波形图
卡诺图与硬件描述语言后面的文章再讲。
三、逻辑函数的两种标准形式
1、最小项与最大项
最小项
在n变量逻辑函数中,若m为包含n个因子的乘积项,而且这n个变量均以原变量或反变量的形式在m中出现一次,则称m为该组变量的最小项。n变量的最小项个数有 个。
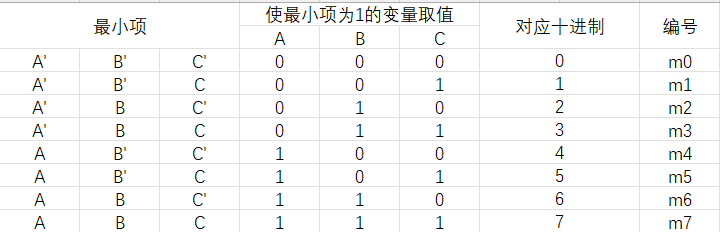
图3.1 三变量最小项的编号表
最小项是与运算,所以要使每一个因子都为1,最终值才能为1。
最小项的性质
①在输入变量的任何取值下必有一个最小项,而且仅有一个最小项的值为1;
②全体最小项之和为1;
③任意两个最小项的乘积为0;
④具有相邻性的两个最小项之和可以合并成一项并消去一对因子。
相邻性:若两个最小项只有一个因子不同,则称这两个最小项聚优品相邻性。比如A'BC'&ABC'就具有相邻性。
A'BC' + ABC' = (A+A')BC'=BC'-------------------------由公式A+A'=1得
最大项
在n变量逻辑函数中,若M为n个变量之和,而且这n个变量均以原变量或反变量的形式在M中出现一次,则称M为该组变量的最大项。

图3.2 三变量最大项的编号表
最大项的性质
①在输入变量的任何取值下必有一个最大项,而且只有一个最大项的值为0;
②全体最大项之和为0;
③任意两个最大项之和为1;
④只有一个变量不同的两个最大项的乘积等于各相同变量之和。
2、最大项与最小项的关系
3、逻辑函数的最小项之和形式
第一步:将给定的逻辑函数化成若干乘积项之和的与或形式(积之和);
第二步:利用公式A+A'=1将缺少的因子补全(凑出ABC)
例1:
也可以写作:Y(A,B,C)=Σm(3,6,7)
4、逻辑函数的最大项之和形式
第一步:将给定的逻辑函数化成若干乘积项之和的或与形式(和之积);
第二步:利用公式A·A'=0将缺少的因子补全(凑出ABC)
例2:Y=A'B+AC=(A+B+C)(A+B+C')(A'+B+C)(A'+B'+C)
也可以写作:Y(A,B,C,D)=ΠM(0,1,4,6)
若文章内容出现错误,恳请各位批评指正,感激不尽!
相关文章:
数电学习笔记——逻辑函数及其描述方法
目录 一、逻辑函数 二、逻辑函数的描述方法 1、逻辑真值表 2、逻辑函数式 3、逻辑图 4、波形图 三、逻辑函数的两种标准形式 1、最小项与最大项 最小项 最小项的性质 最大项 最大项的性质 2、最大项与最小项的关系 3、逻辑函数的最小项之和形式 4、逻辑函数的最…...

2024年护眼台灯哪家品牌好?五款优质品牌专业推荐
护眼台灯几乎是每个孩子书桌上都会有的灯具,但还是有不少家长觉得是“智商税”。其实护眼台灯好处非常多,列如能够提供舒适的照明,缓解用眼疲劳,预防近视等等。所以今天准备了一期护眼台灯测评,并附上护眼台灯的榜单&a…...

搜索iconfont或者阿里图标就可以得到免费的图标
你在搜索过程中就会出现一些无耻,不要脸的网站,比如说下面这个 这个才是阿里图标 看它的网址 都是免费的...

android实战视频教程,细数Android开发者的艰辛历程
缘起 随着互联网企业的不断发展,产品项目中的模块越来越多,用户体验要求也越来越高,想实现小步快跑、快速迭代的目的越来越难,还有应用之间的互相调用等等问题,插件化技术应用而生。如果没有插件化技术,美…...

nav2_gps_waypoint_follower_demo 不能在ros2 humble中直接使用的解决方法
GIT上的nav2_gps_waypoint_follower_demo是基于ros-iron编写的,其中followGpsWaypoints(wps) service只能在Iron上使用。 解决方法: 第一步:将interactive_waypoint_follower.py修改为如下代码: import rclpy from rclpy.node …...

华为OD机试 - 螺旋数字矩阵
1 题目描述 疫情期间,小明隔离在家,百无聊赖,在纸上写数字玩。他发明了一种写法: 给出数字个数 n (0 < n ≤ 999)和行数 m(0 < m ≤ 999),从左上角的 1 开始&…...

Vue响应式内容丢失处理
对数组和对象进行不当的修改会使Vue的对象丢失响应式,这时可以直接console.log丢失的对象,看是否有getter和setter 对于数组和对象,只有使用 Vue 提供的一些方法(如 push()、pop()、splice()、set() 等)进行修改才会触…...

Linux安装Rabbitmq
说明:本文章主要是rabbitmq在Linux系统上的安装,文章中包含了rabbitmq的下载及依赖下载 1.版本选取,这里的选取主要是版本的兼容问题 去这个网址查看mq和erlang版本兼容:RabbitMQ Erlang Version Requirements | RabbitMQ 2.相…...

在nginx 服务器部署vue项目
以人人快速开发的开源项目:renren-fast-vue 为例 注:这里开始认为各位都会使用nginx 打包vue项目 npm run build 测试打包的项目是否可以运行 serve dist 可以正常运行 编译报错请移步到:renren-fast-vue1.2.2 项目编译报错: build g…...
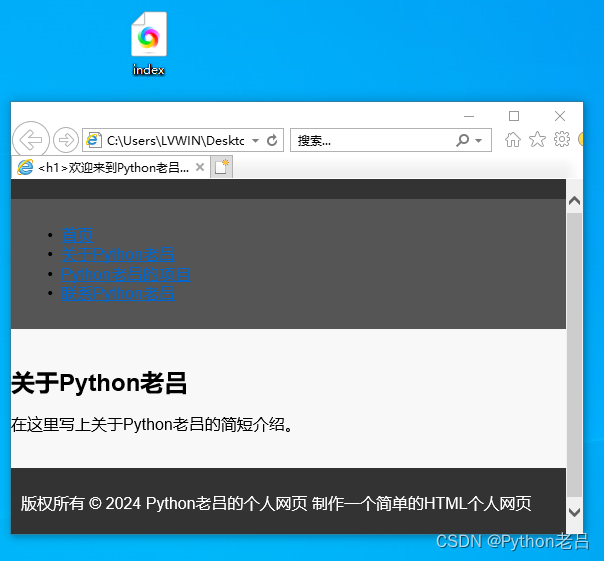
制作一个简单的HTML个人网页
制作一个简单的HTML个人网页 1.1 硬件1.1.1 一台电脑1.1.2 配置要求 1.2 系统1.3 软件 二、制作一个简单的HTML个人网页1.创建一个HTML网页1.1 新建文本文档1.2 另存文本文档1.3 命名为index.html 2.编写HTML代码2.1 打开HTML2.2 复制HTML代码2.3 粘贴HTML代码2.4 保存HTML 3.预…...
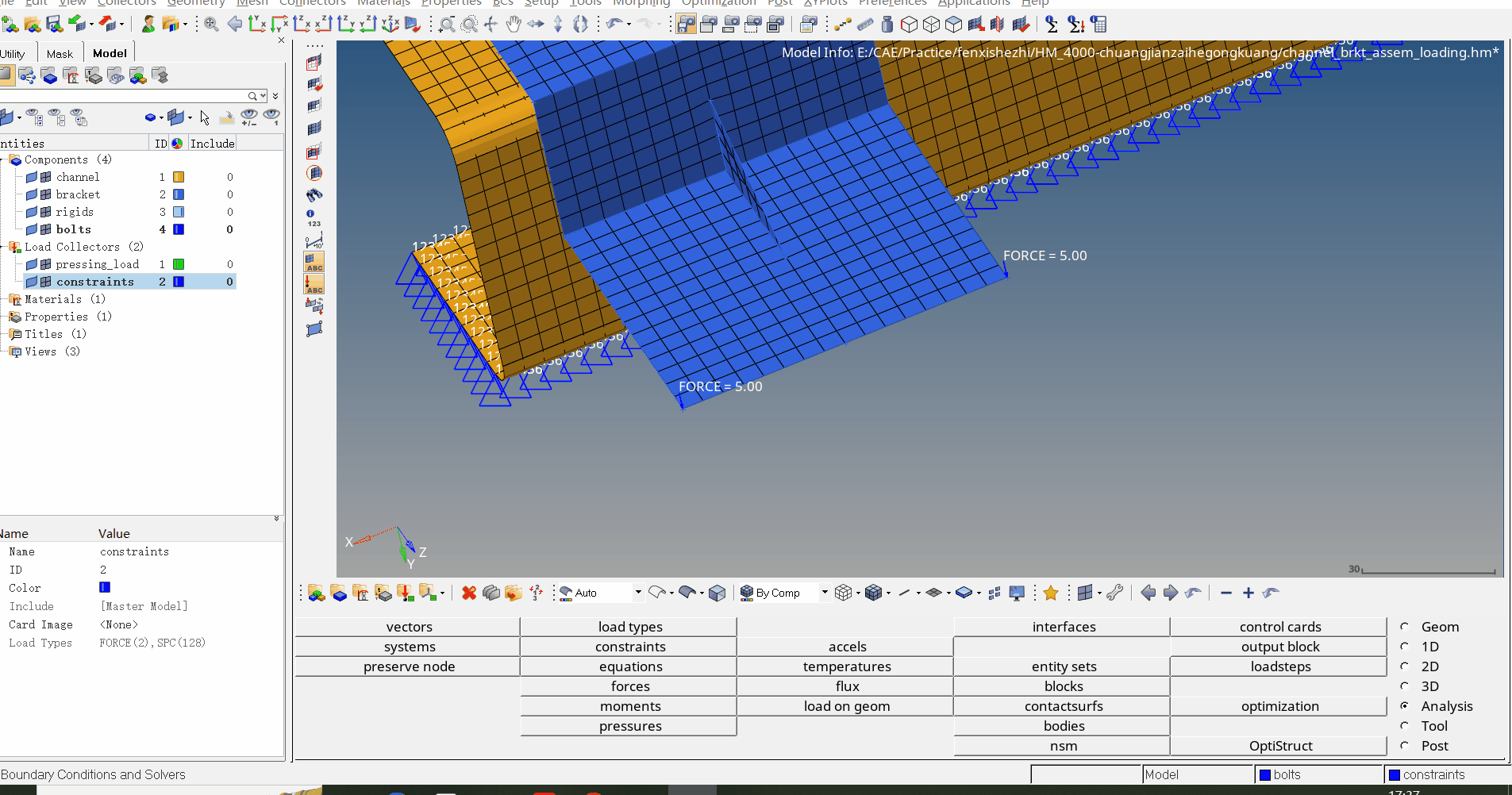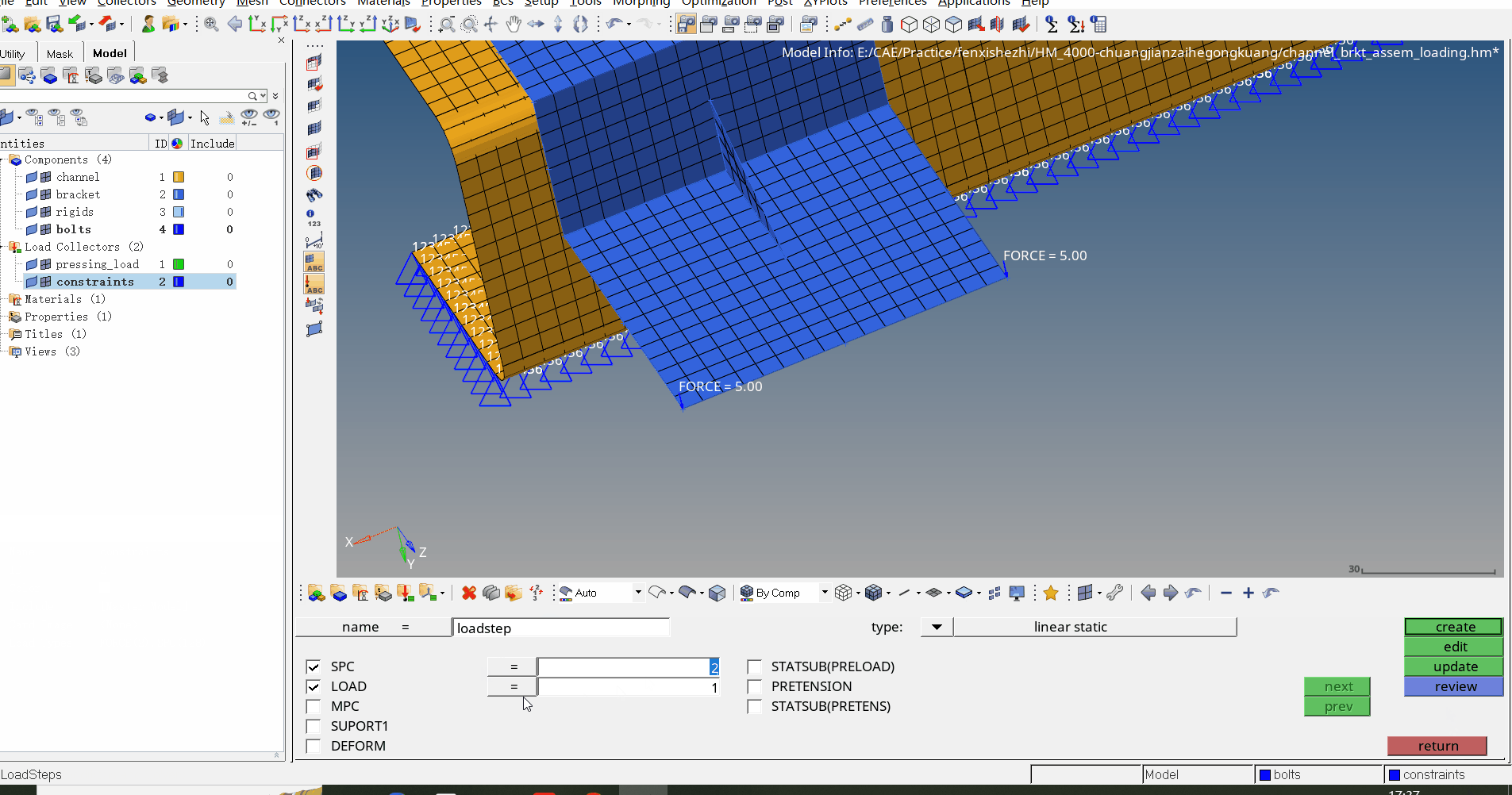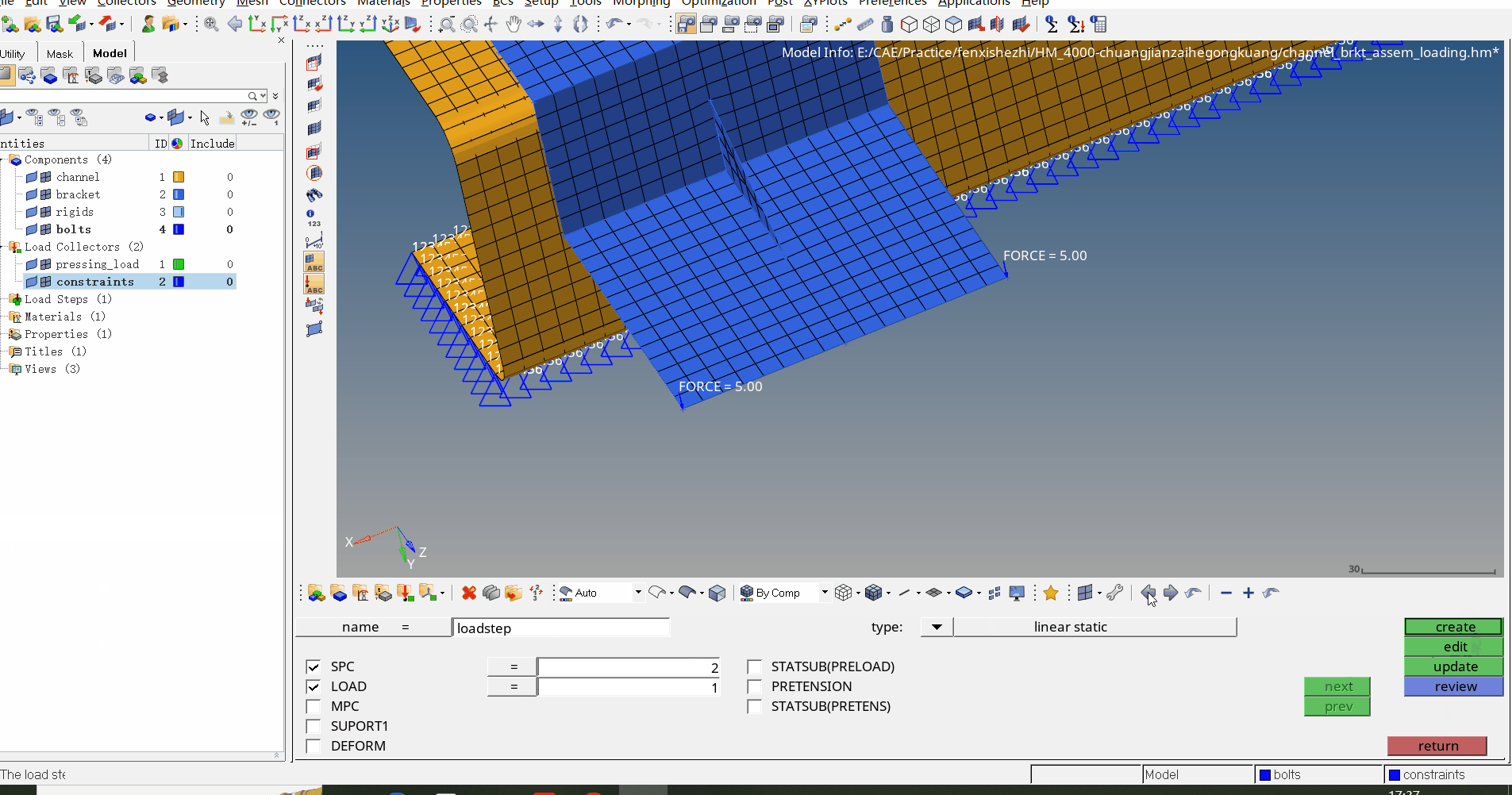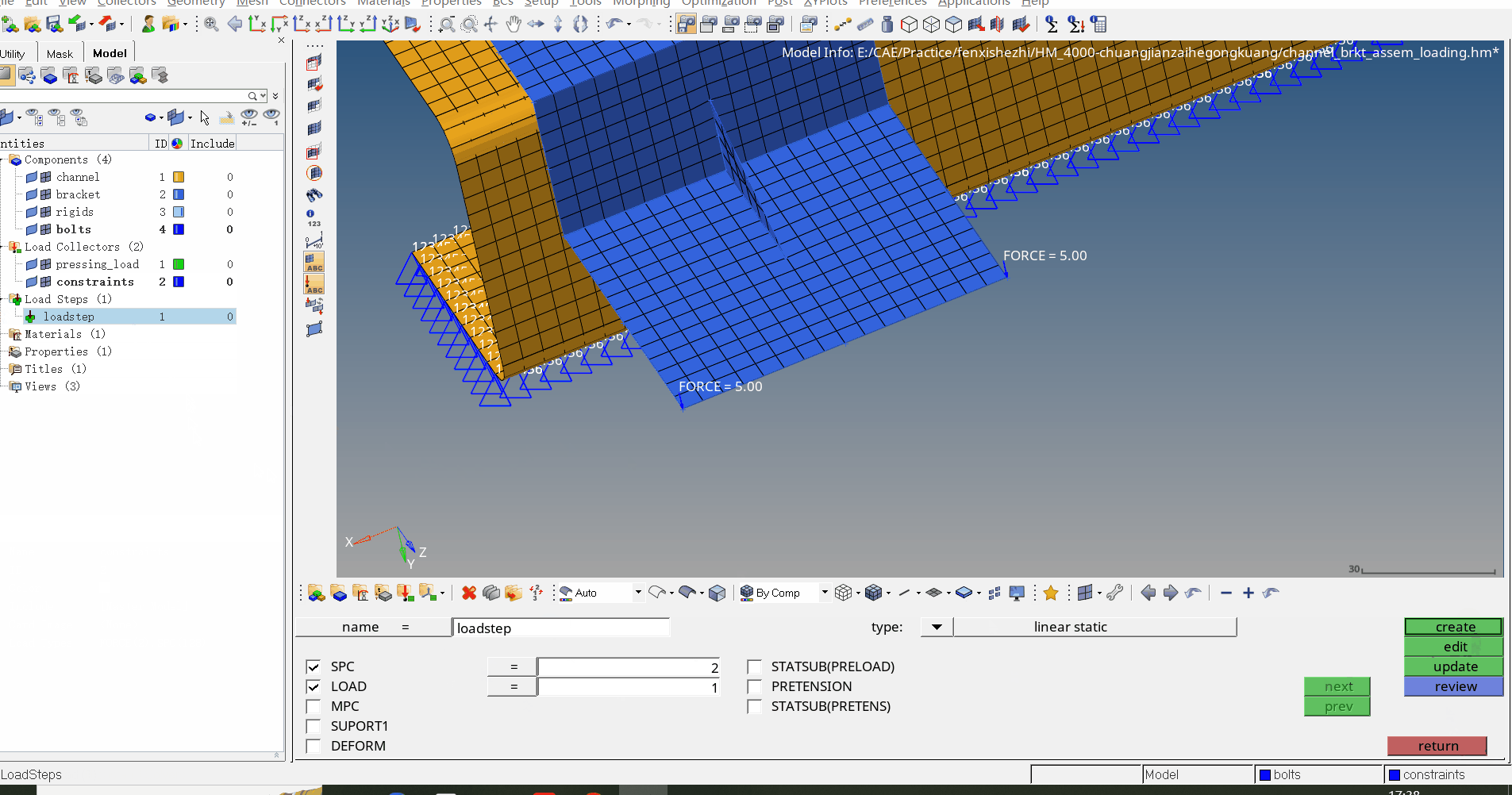
HM2019创建载荷工况
该案例中将介绍载荷、工况、约束的创建 步骤一:首先创建两个载荷集(Load Collector)用来存放载荷和约束 步骤二:在Analysis面板下创建约束(Analysis→constraints) 注意:Load type选择SPC表示统计过程控制(Statistical Process Control) 步…...

Effective C++ 学习笔记 条款14 在资源管理类中小心copying行为
条款13导入这样的观念:“资源取得时机便是初始化时机”(Resource Acquisition Is Initialization,RAII),并以此作为“资源管理类”的脊柱,也描述了auto_ptr和tr1::shared_ptr如何将这个观念表现在heap-base…...
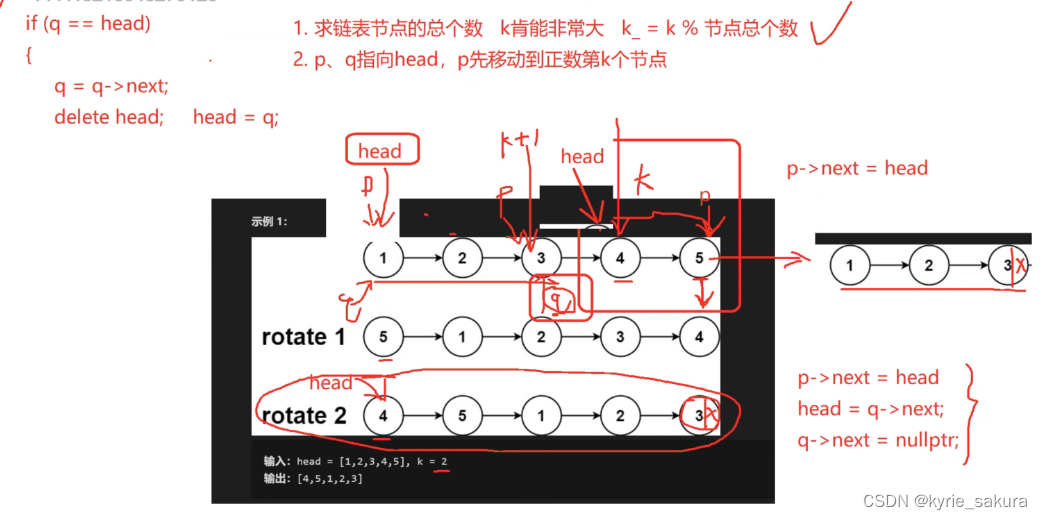
c++数据结构算法复习基础-- 3 --线性表-单向链表-笔试面试常见问题
1、单链表逆序 思路图 代码实现 //著: 链表结构里记得加 friend void ReverseLink(Clink& link); void ReverseLink(Clink& link) {Node* p link.head_->next_;while( p nullptr){return;}Node* q p->next_;link.head_->next_ nullptr;while(p ! nullpt…...

【踩坑专栏】追根溯源,从Linux磁盘爆满排查故障:mycat2与navicat不兼容导致日志暴增
昨天遇到了一个比较奇怪的问题,就是在挂起虚拟机的时候,虚拟机提示我XX脚本正在运行,很奇怪,我没有运行脚本,为什么会提示我这个呢。今天恢复虚拟机,也提示了一下脚本的问题,而且发现Linux明显异…...
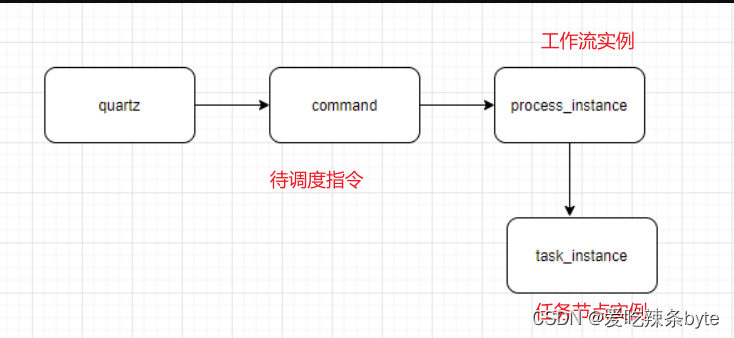
DolphinScheduler——奇富科技的调度实践
目录 一、技术架构 二、业务挑战 2.1 调度任务量大 2.2 运维复杂 2.3 SLA要求高 三、调度优化实践 3.1 重复调度 3.2 漏调度 3.3 Worker服务卡死 3.4 任务重复运行 四、服务监控 4.1 方法耗时监控 4.2 任务调度链路监控 五、用户收益 原文大佬的这篇调度系统案例…...

2024年最全洗地机选购攻略盘点丨希亦、小米、云鲸、海尔洗地机哪款值得入手?
在现代家居清洁中,洗地机是不可或缺的得力助手,它融合了吸尘、拖地等多种功能。面对市场上琳琅满目的洗地机品牌和型号,选择一个可靠的品牌至关重要。优质的品牌能够提供高品质的产品,使您的清洁工作更加轻松高效。本文将向您推荐…...

HTML笔记3
21,label标签 <label for"...">...</label> <label>...</label> <!DOCTYPE html> <html lang"en"> <head> <meta charset"UTF-8"> <meta name"viewport" content&qu…...

利用Python副业赚钱,看完这篇你就懂了!
Python都可以做哪些副业? 1、兼职处理数据Excel整理数据功能虽然很强大,但在Python面前,曾经统治职场的它也的败下阵来。因为Python在搜集数据整理分析数据的过程中更加便捷,通过几行代码还可以实现自动化操作。 如果你学会Pyth…...
、FP32(单精度浮点数)和INT8)
FP16(半精度浮点数)、FP32(单精度浮点数)和INT8
在深度学习和计算机视觉领域中,FP16(半精度浮点数)、FP32(单精度浮点数)和INT8(8 位整数)是常见的数据类型或精度表示方式。它们在不同的场景下有各自的优势和用途。 FP16(半精度浮…...

MySQL数据管理二
1.数据库的完整性 数据库中的数据是从外界输入的,而数据的输入由于种种原因,会发生输入无效或错误信息。保证输入的数据符合规定,成为了数据库系统,尤其是多用户的关系数据库系统首要关注的问题。 它是应防止数据库中存在不符合语…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...

离线语音识别方案分析
随着人工智能技术的不断发展,语音识别技术也得到了广泛的应用,从智能家居到车载系统,语音识别正在改变我们与设备的交互方式。尤其是离线语音识别,由于其在没有网络连接的情况下仍然能提供稳定、准确的语音处理能力,广…...

【Kafka】Kafka从入门到实战:构建高吞吐量分布式消息系统
Kafka从入门到实战:构建高吞吐量分布式消息系统 一、Kafka概述 Apache Kafka是一个分布式流处理平台,最初由LinkedIn开发,后成为Apache顶级项目。它被设计用于高吞吐量、低延迟的消息处理,能够处理来自多个生产者的海量数据,并将这些数据实时传递给消费者。 Kafka核心特…...

C++_哈希表
本篇文章是对C学习的哈希表部分的学习分享 相信一定会对你有所帮助~ 那咱们废话不多说,直接开始吧! 一、基础概念 1. 哈希核心思想: 哈希函数的作用:通过此函数建立一个Key与存储位置之间的映射关系。理想目标:实现…...
