代码随想录算法训练营day38|理论基础、509. 斐波那契数、70. 爬楼梯、746. 使用最小花费爬楼梯
理论基础
代码随想录
视频:从此再也不怕动态规划了,动态规划解题方法论大曝光 !| 理论基础 |力扣刷题总结| 动态规划入门_哔哩哔哩_bilibili
动态规划:如果某一问题有很多重叠子问题,使用动态规划是最有效的。所以动态规划中每一个状态一定是由上一个状态推导出来的,这一点就区分于贪心,贪心没有状态推导,而是从局部直接选最优的
对于动态规划问题,要搞清楚以下几点:
- 确定dp数组(dp table)以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数组
509. 斐波那契数
代码随想录
视频:手把手带你入门动态规划 | LeetCode:509.斐波那契数_哔哩哔哩_bilibili
动态规划五部曲:
1.确定dp[i]的含义:第i个数的斐波那契数值为dp[i]
2.确定递推公式:dp[i] = dp[i-1]+dp[i-2]
3.dp数组如何初始化:dp[0]=0,dp[1]=1
4.遍历顺序:从递归公式dp[i] = dp[i - 1] + dp[i - 2];中可以看出,dp[i]是依赖 dp[i - 1] 和 dp[i - 2],那么遍历的顺序一定是从前到后遍历的
5.举例推导dp数组
按照这个递推公式dp[i] = dp[i - 1] + dp[i - 2],我们来推导一下,当N为10的时候,dp数组应该是如下的数列:
0 1 1 2 3 5 8 13 21 34 55
如果代码写出来,发现结果不对,就把dp数组打印出来看看和我们推导的数列是不是一致的。
class Solution:def fib(self, n: int) -> int:if n < 2:return 0dp = [0]* (n+1)dp[0]=0dp[1]=1for i in range(2,n+1):dp[i] = dp[i-1] + dp[i-2]return dp[n]
也可以只维护两个数值:
class Solution:def fib(self, n: int) -> int:if n <= 1:return ndp = [0, 1]for i in range(2, n + 1):total = dp[0] + dp[1]dp[0] = dp[1]dp[1] = totalreturn dp[1]递归法:
class Solution:def fib(self, n: int) -> int:if n == 0:return 0if n== 1:return 1return self.fib(n-1)+self.fib(n-2)70. 爬楼梯
代码随想录
视频:带你学透动态规划-爬楼梯(对应力扣70.爬楼梯)| 动态规划经典入门题目_哔哩哔哩_bilibili
到第三层楼梯的状态可以由第二层楼梯 和 到第一层楼梯状态推导出来,那么就可以想到动态规划
1.确定dp[i]的含义:爬到第i层楼梯,有dp[i]种方法
2.确定递推公式:dp[i] = dp[i-1]+dp[i-2]
3.dp数组如何初始化:dp[1]=1,dp[2]=2
4.遍历顺序:从递归公式dp[i] = dp[i - 1] + dp[i - 2];中可以看出,dp[i]是依赖 dp[i - 1] 和 dp[i - 2],那么遍历的顺序一定是从前到后遍历的
5.举例推导dp数组
class Solution:def climbStairs(self, n: int) -> int:dp = [0]*(n+1)dp[1] = 1dp[2] = 2for i in range(3,n+1):dp[i] = dp[i-1] + dp[i-2]return dp[n]746. 使用最小花费爬楼梯
代码随想录
视频讲解:动态规划开更了!| LeetCode:746. 使用最小花费爬楼梯_哔哩哔哩_bilibili
1.确定dp[i]的含义:爬到第i层楼梯,有dp[i]种方法
2.确定递推公式:dp[i] = min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2])
3.dp数组如何初始化:dp[0]=0,dp[1]=0
4.遍历顺序:从递归公式dp[i] = dp[i - 1] + dp[i - 2];中可以看出,dp[i]是依赖 dp[i - 1] 和 dp[i - 2],那么遍历的顺序一定是从前到后遍历的
5.举例推导dp数组
class Solution:def minCostClimbingStairs(self, cost: List[int]) -> int:dp = [0]*(len(cost)+1)dp[0] = 0dp[1] = 0for i in range(2,len(cost)+1):dp[i] = min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2])return dp[len(cost)]相关文章:

代码随想录算法训练营day38|理论基础、509. 斐波那契数、70. 爬楼梯、746. 使用最小花费爬楼梯
理论基础 代码随想录 视频:从此再也不怕动态规划了,动态规划解题方法论大曝光 !| 理论基础 |力扣刷题总结| 动态规划入门_哔哩哔哩_bilibili 动态规划:如果某一问题有很多重叠子问题,使用动态规划是最有效的。所以动态…...

夫妻一方名下股权到底归谁?
生效判决摘要:1.夫妻一方在婚姻关系存续期间投资的收益,为夫妻的共同财产,归夫妻共同所有,但是并不能据此否定股权本身可能成为夫妻共同财产。婚姻关系存续期间登记在配偶一方名下的股权能否成为夫妻共同财产,可由司法…...
git根据文件改动将文件自动添加到缓冲区
你需要修改以下脚本中的 use_cca: false 部分 #!/bin/bash# 获取所有已修改但未暂存的文件 files$(git diff --name-only)for file in $files; do# 检查文件中是否存在"use_cca: false"if grep -q "use_cca: false" "$file"; thenecho "Ad…...

SystemVerilog Constants、Processes
SystemVerilog提供了三种类型的精化时间常数: •参数:与最初的Verilog标准相同,可以以相同的方式使用。 •localparameter:与参数类似,但不能被上层覆盖模块。 •specparam:用于指定延迟和定时值&#x…...

交易平台开发:构建安全/高效/用户友好的在线交易生态圈
在数字化浪潮的推动下,农产品现货大宗商品撮合交易平台已成为连接全球买家与卖家的核心枢纽。随着电子商务的飞速发展,一个安全、高效、用户友好的交易平台对于促进交易、提升用户体验和增加用户黏性至关重要。本文将深入探讨交易平台开发的关键要素&…...

Linux系统之部署复古游戏平台
Linux系统之部署复古游戏平台 前言一、项目介绍1.1 项目简介1.2 项目特点1.3 游戏平台介绍二、本次实践介绍二、本地环境介绍2.1 本地环境规划2.2 本次实践介绍三、本地环境检查3.1 安装Docker环境3.2 检查Docker服务状态3.3 检查Docker版本3.4 检查docker compose 版本四、构建…...

开源计算机视觉库opencv-python详解
开源计算机视觉库opencv-python详解 OpenCV-Python的核心功能:安装OpenCV-Python:使用OpenCV-Python的基本步骤:OpenCV-Python的高级应用:注意事项:OpenCV-Python的高级应用示例:1. 人脸识别2. 目标跟踪3. …...

Vue开发实例(十)Tabs标签页打开、关闭与路由之间的关系
创建标签页 一、创建标签页二、点击菜单展示新标签页1、将标签数据作为全局使用2、菜单点击增加标签页3、处理重复标签4、关闭标签页 三、点击标签页操作问题1:点击标签页选中菜单进行高亮展示问题2:点击标签页路由也要跳转 四、解决bug 先展示最终效果 …...

基于51单片机的智能火灾报警系统
基于51单片机的智能火灾报警系统 摘要: 本文提出了一种基于51单片机的智能火灾报警系统。该系统采用烟雾传感器和温度传感器来检测火灾的发生,并通过单片机进行数据处理和报警控制。此外,该系统还具有无线通信功能,可以实时将火灾…...

【数据结构】堆的TopK问题
大家好,我是苏貝,本篇博客带大家了解堆的TopK问题,如果你觉得我写的还不错的话,可以给我一个赞👍吗,感谢❤️ 目录 一. 前言二. TopK三. 代码 一. 前言 TOP-K问题:即求数据结合中前K个最大的元…...

Vue后台管理系统笔记-01
npm(Node Package Manager)和 yarn 是两个常用的包管理工具,用于在 Node.js 项目中安装、管理和更新依赖项。它们有以下几个区别: 性能和速度:在包的安装和下载方面,yarn 通常比 npm 更快速。yarn 使用了并…...
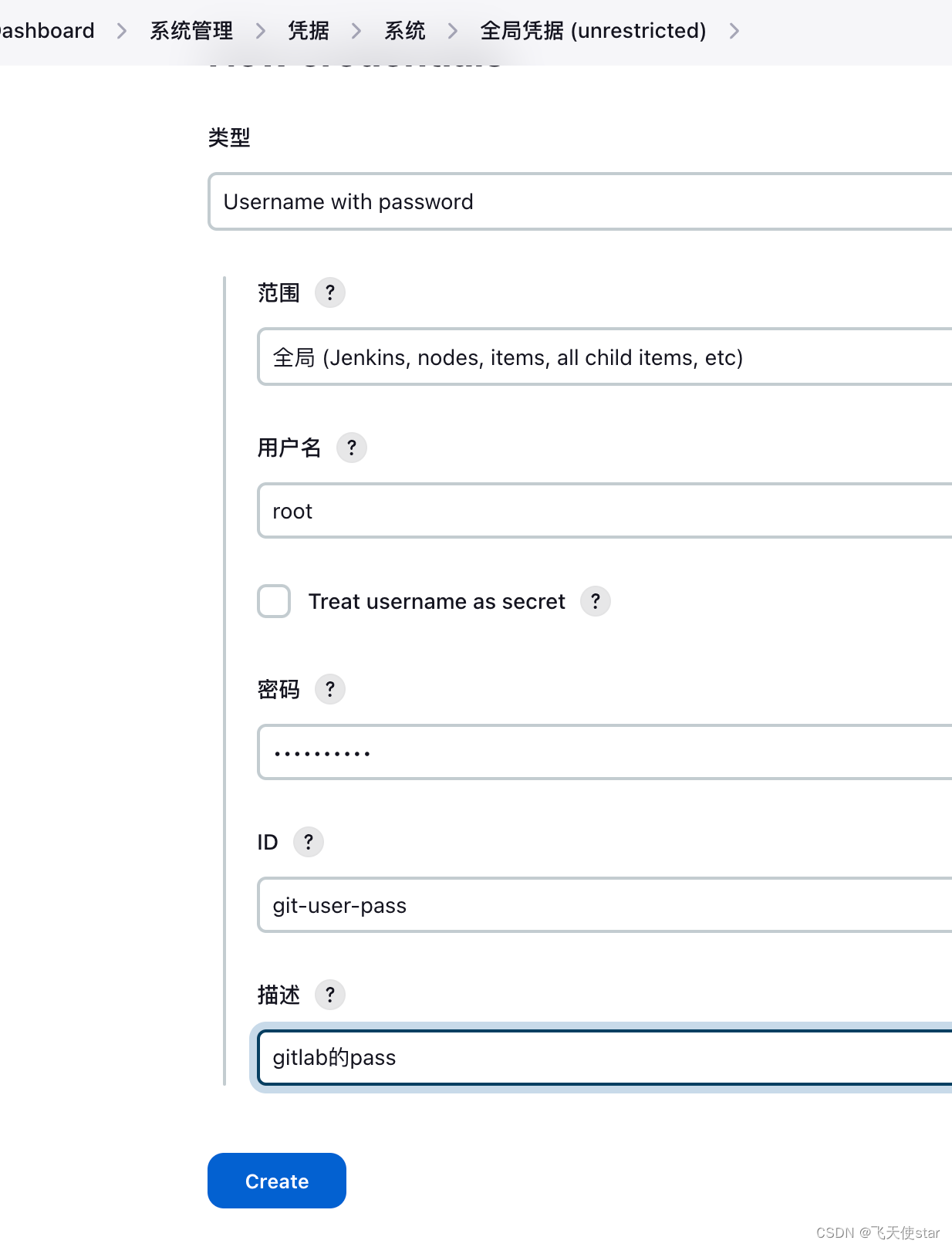
飞天使-学以致用-devops知识点3-安装jenkins
文章目录 构建带maven环境的jenkins 镜像安装jenkinsjenkins yaml 文件安装插件jenkins 配置k8s创建用户凭证 构建带maven环境的jenkins 镜像 # 构建带 maven 环境的 jenkins 镜像 docker build -t 192.168.113.122:8858/library/jenkins-maven:jdk-11 .# 登录 harbor docker …...

08、MongoDB -- MongoDB 的 集合关联($lookup 和 DBRef 实现集合关联)
目录 MongoDB 的 集合关联演示前提:登录单机模式的 mongodb 服务器命令登录【test】数据库的 mongodb 客户端命令登录【admin】数据库的 mongodb 客户端命令 SQL 术语 与 Mongodb 的对应关系使用 $lookup 实现集合关联语法格式添加测试数据1、查询出订单数量大于6&a…...

前方高能,又一波Smartbi签约喜报来袭
近期,交通银行、厦门国际银行、中原农业保险、江苏中天科技等多家知名企业签约Smartbi,携手Smartbi实现数据驱动业务新增长。 Smartbi数10年专注于商业智能BI与大数据分析软件与服务,为各行各业提供提供一站式商业智能平台(PaaS&a…...

蓝桥杯倒计时 41天 - 二分答案-最大通过数-妮妮的月饼工厂
最大通过数 思路:假设左边能通过 x 关,右边能通过 y 关,x∈[0,n],通过二分,在前缀和中枚举右边通过的关卡数,保存 xy 的最大值。 #include<bits/stdc.h> using namespace std; typedef long long ll…...

【JavaSE】泛型
系列文章目录 提示:写完文章后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 系列文章目录前言一、pandas是什么?二、使用步骤 1.引入库2.读入数据总结 前言 学习泛型之前请大家先详细地了解一下,关于Java…...

APS(高级计划与调度系统)难度超高,ERP在它面前就是弟弟。
一、APS定义和功能模块 APS系统是Advanced Planning and Scheduling System(高级计划与调度系统)的缩写。它是一种计划和调度管理软件系统,旨在帮助企业优化生产计划和资源调度,提高生产效率和响应能力。 APS系统利用先进的算法和…...

ArmV8架构
Armv8/armv9架构入门指南 — Armv8/armv9架构入门指南 v1.0 documentation 上面只是给了一个比较好的参考文档 其他内容待补充...

[论文笔记] Open-sora 2、视频数据集介绍 MSR-VTT
MSR-VTT COVE - Computer Vision Exchange 论文参考:https://www.microsoft.com/en-us/research/wp-content/uploads/2016/06/cvpr16.msr-vtt.tmei_-1.pdf 用于视频理解的大规模视频基准,特别是将视频翻译为文本的新兴任务。这是通过从商业视频搜索引擎收集 257 个热门查询…...

【Windows 常用工具系列 14 -- windows 网络驱动映射】
文章目录 windows 网络驱动映射 windows 网络驱动映射 映射网络驱动器的意思是将局域网中的某个目录映射成本地驱动器号。 在windows上将服务器目录映射到本地盘: 进入到服务器执行下面命令既可以看到对应的 IP地址: 将对应的IP地址填入上图中。 映…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...
