回溯算法01-组合(Java)
1.组合
- 题目描述
给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。
你可以按 任何顺序 返回答案。
示例 1:
输入:n = 4, k = 2
输出:
[[2,4],[3,4],[2,3],[1,2],[1,3],[1,4]]
示例 2:
输入:n = 1, k = 1
输出:[[1]]
- 题目分析
根据题目可知,本题是求1-n这n个不同的数的组合问题,我们知道对于n个不同的数中的任意k个数组合,当n很大时通过枚举是很难将它枚举完成的,所以我们可以采用回溯算法来解决这一类问题。
- 回溯算法的模板
1.确立递归函数及返回值
2.确立回溯的终止条件
3.单层递归逻辑
private void backtracking(参数) {//回溯的终止条件if (终止条件) {存放结果;return;}//回溯算法的遍历过程(集合的大小为树的宽度,递归的深度为树的深度)for (选择 :本层集合的元素) {处理节点;backtracking(路径, 选择列表);//递归回溯,撤销处理的结果}
}
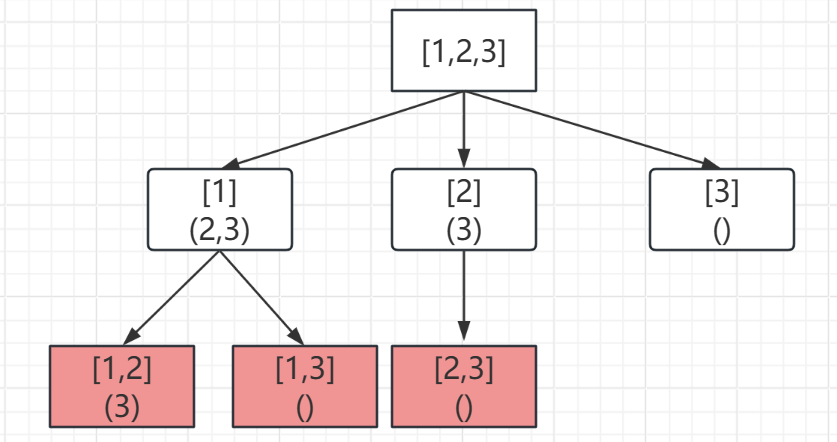
1.首先我们确立递归函数及参数(例子:nums=[1,2,3] k = 2)
根据下图递归操作我们可以看出,每次挑选数组nums中的一个元素加入到集合之中:
第一次:集合元素为[1],剩余元素为[2,3]
第二次:集合元素为[1,2],剩余元素为[3] 此时集合[1,2]满足k = 2的组合条件,将其存储,因为之后不再再取3会使不满足k个数组合的条件,因此要进行回溯,返回到集合元素为[1],剩余元素为[2,3]
第三次:集合元素为[1,3],剩余元素为[] 此时要选择元素3加入到集合,因此我们要设置一个索引来避开元素2,这样才不会有重复
...依次回溯,我们发现每次叶子节点为我们想要的结果所以初始化一个回溯函数
void backtrack(int nums[], int startIndex) {}
nums为要组合的元素集合,startIndex为避免每次重复的指针2.设置终止条件:当我们组合的集合中恰好有k个节点时,表示组合完成3.单层递归逻辑
从startIndex开始,遍历所有可能的元素,将其添加到路径中,并递归调用backtrace方法继续生成下一个元素。完成递归后,需要将最后一个元素从路径中移除,以便尝试其他可能的元素。
- 以nums=[1,2,3,4] k = 2直观感受一下i与startIndex的变化
i = 1 s = 1 [1]
i = 2 s = 2 [1,2]
//i = 2 s = 2 [1]
i = 3 s = 2 [1,3]
//i = 3 s = 2 [1]
i = 4 s = 2 [1,4]
//i = 4 s = 2 [1]
i = 2 s = 1 [2]
i = 3 s = 3 [2,3]
//i = 3 s = 3 [2]
i = 4 s = 3 [2,4]
//i = 4 s = 3 [2]
i = 3 s = 1 [3]
...
- Java代码实现
//list:用于存储一条路径上的元素//result:用于返回最后的元素LinkedList<Integer> path = new LinkedList<>();List<List<Integer>> result = new LinkedList<>();public List<List<Integer>> combine(int n, int k) {backtrace(n, k, 1);return result;}//1.确立递归函数的参数及返回值//n:树的宽度即求n个数的组合数//k:叶子节点即组合个数为k//startIndex:用于开始元素遍历的起点private void backtrace(int n, int k, int startIndex) {//2.确立终止条件if (path.size() == k) {//当最后组成的元素集合为k时返回结果result.add(new LinkedList<>(path));return;}//3.单层递归逻辑for (int i = startIndex; i <= n; i++) {path.add(i);backtrace(n, k, i + 1);path.removeLast();}}
相关文章:

回溯算法01-组合(Java)
1.组合 题目描述 给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。 你可以按 任何顺序 返回答案。 示例 1: 输入:n 4, k 2 输出: [[2,4],[3,4],[2,3],[1,2],[1,3],[1,4]]示例 2: 输入&#x…...
初始网络 --- 网络基础
目录 0、 前言 1、 计算机网络发展背景 1.1. 局域网(LAN) && 广域网(WAN) 2、 认识并理解协议 3、 初始网络协议 3.1. 协议分层 4、 TCP/IP 五层(或四层)模型 4.1. 简单了解TCP/IP层状体系 4.2. TCP/IP协议层状结构和计算机层状结构的关系 5、 OSI七层模型 …...

在Linux/Ubuntu/Debian中计算MD5,SHA256的方法
MD5(消息摘要算法 5)和 SHA-256(安全哈希算法 256 位)等流行的哈希算法广泛用于从任意数据生成固定大小的哈希值或校验和。 以下是这些算法及其计算方式的简要概述: MD5(消息摘要算法5)&#x…...

mybatis mysql insert 主键id为空
错误示范 java代码设置了param参数,但是sql 字段没有带上参数,例如 void insertV2(Param("historyDO") HistoryDO historyDO); <insert id"insertDuplicate" parameterType"com.test.entity.HistoryDO"keyProperty&…...

批次大小对ES写入性能影响初探
问题背景 ES使用bulk写入时每批次的大小对性能有什么影响?设置每批次多大为好? 一般来说,在Elasticsearch中,使用bulk API进行批量写入时,每批次的大小对性能有着显著的影响。具体来说,当批量请求的大小增…...

c语言十大核心用法
当然,以下是十个关于 C 语言用法的代码示例: 指针的基本用法: #include <stdio.h>int main() {int num 10;int *ptr;ptr #printf("The value of num is: %d\n", *ptr);return 0; }结构体的使用: #in…...
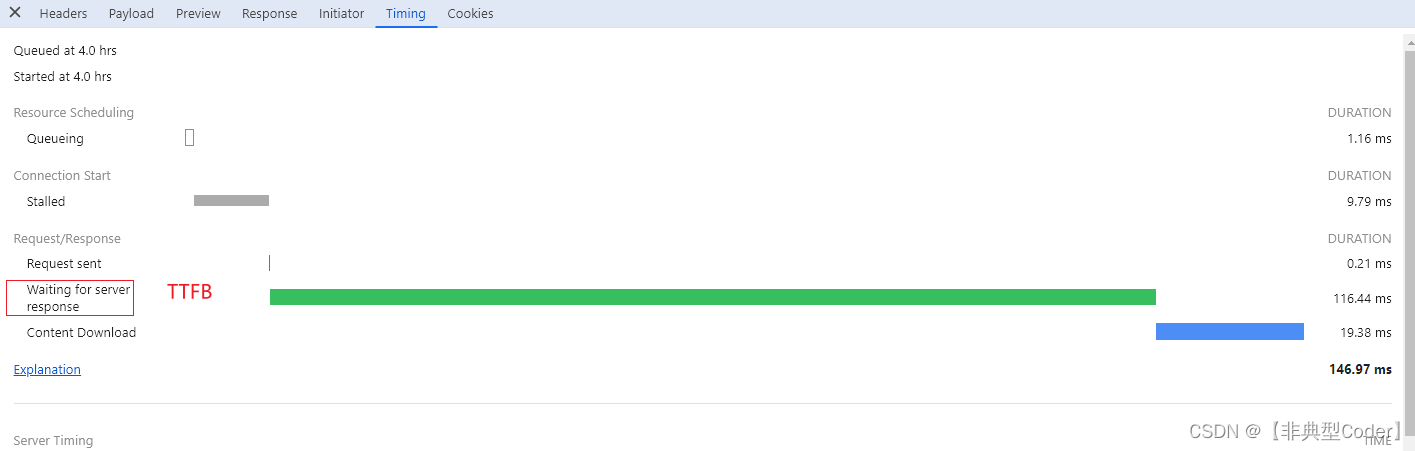
网页打开慢,这锅该谁背?
一、背景 工作中扯皮说不可避免且非常常见的事情. 开发与产品、开发和测试、前端和后端都会产生扯皮现象。今天要聊的一个问题就是前后端之间的扯皮问题。 网页打开太慢或者点击了某个按钮发现数据很久才显示出来,这个锅谁背? 做开发不能无凭据地胡乱甩锅, 我们…...

题目 1538: 蓝桥杯-格子位置
题目描述: 输入三个自然数N,i,j (1< i< N,1< j< N),输出在一个N*N格的棋盘中,与格子(i,j)同行、同列、同一对角线的所有格子的位置。 样例解释…...
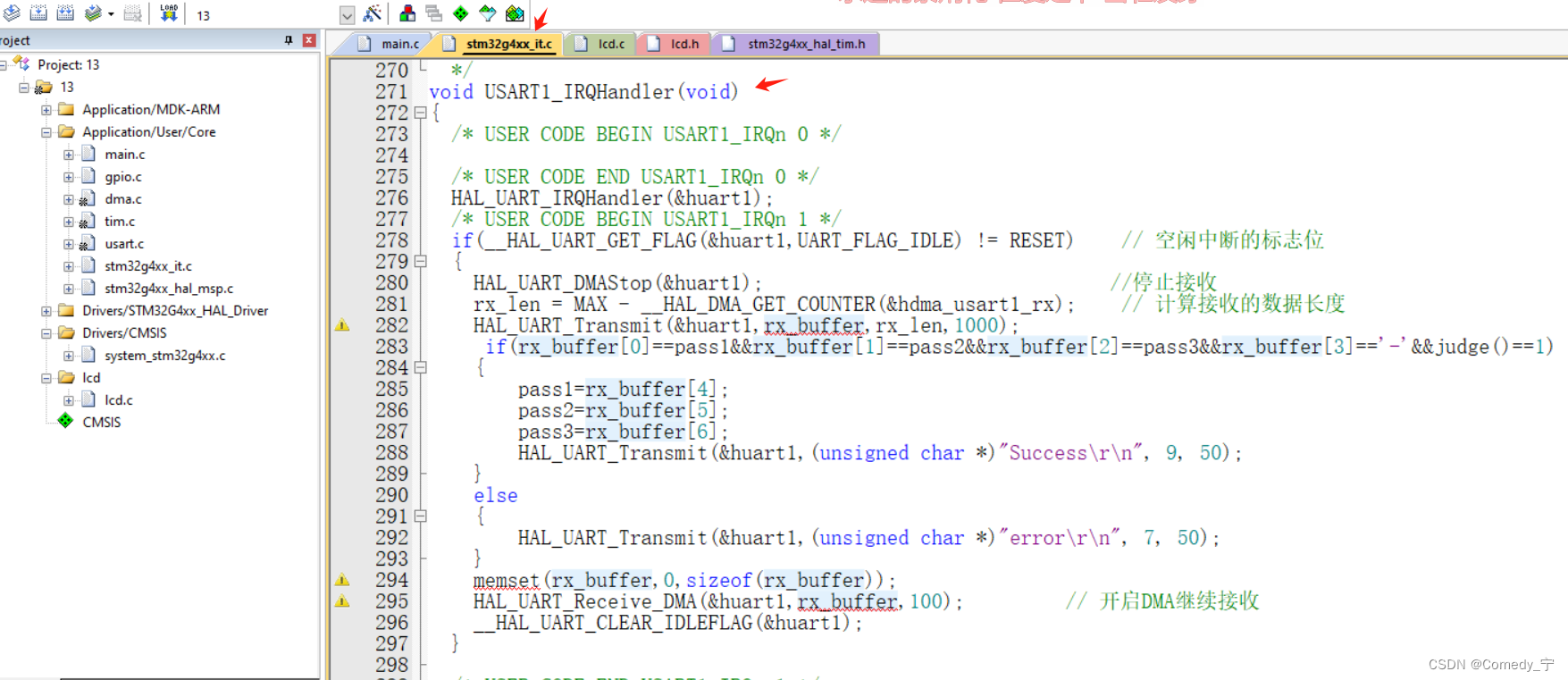
第十三届蓝桥杯嵌入式省赛程序设计详细题解
第十三届蓝桥杯嵌入式省赛题目相对于第十二届较为简单,没有那么多串口的数据处理以及判断! 第十三届省赛主要是制作一个可由串口设置密码的密码锁。本实验中,我们将用到LED模块、按键模块、串口模块、定时器的PWM模块以及官方会提供源码的LC…...

Go 语言指针
1. 什么是指针? 在 Go 语言中,指针是一种特殊的数据类型,它存储了一个变量的内存地址。指针提供了直接访问和修改变量值的能力。 2. 指针的基本操作 2.1 声明指针 在 Go 中声明指针需要使用 * 符号,例如: var p *…...

指针运算笔试题解析
题目1: int main() { int a[5] { 1, 2, 3, 4, 5 }; int* ptr (int*)(&a 1); printf("%d %d", *(a 1), *(ptr - 1)); return 0; } ptr中存放了整个数组的地址,ptr是int*类型,&a1跳到5的地址后又被强制类…...
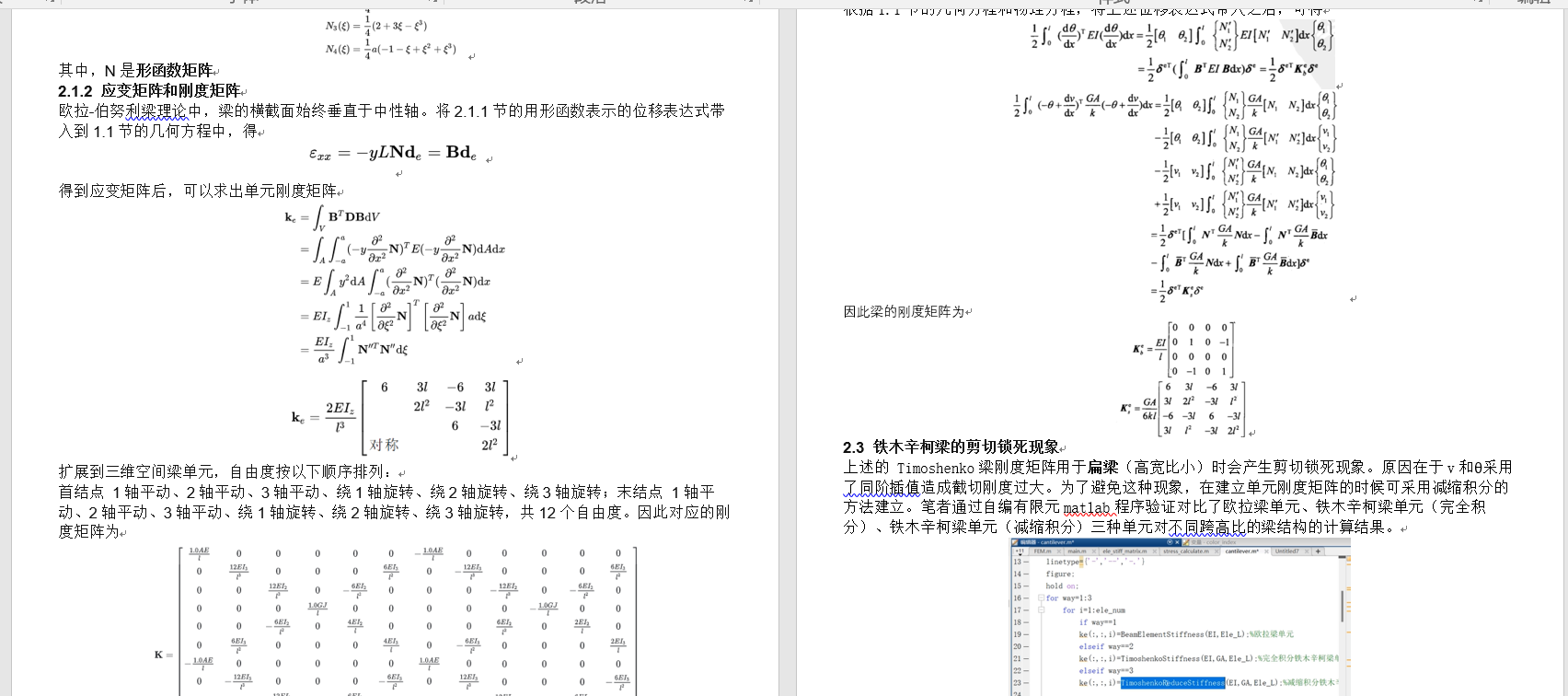
Matlab梁单元有限元编程 | 铁木辛柯梁 | 欧拉梁 | Matlab源码 | 理论文本
专栏导读 作者简介:工学博士,高级工程师,专注于工业软件算法研究本文已收录于专栏:《有限元编程从入门到精通》本专栏旨在提供 1.以案例的形式讲解各类有限元问题的程序实现,并提供所有案例完整源码;2.单元…...
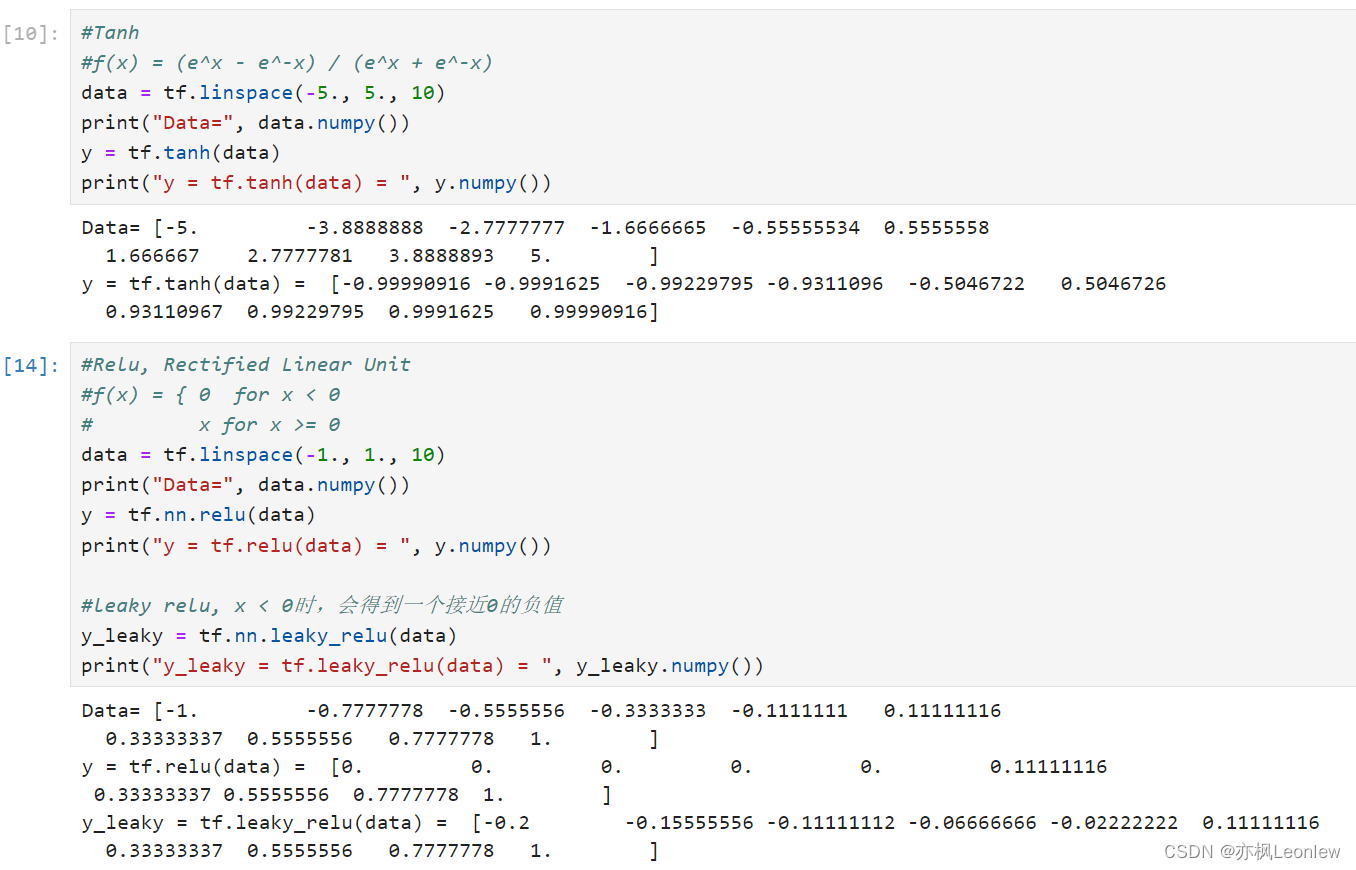
Tensorflow2.0笔记 - 常见激活函数sigmoid,tanh和relu
本笔记主要记录常见的三个激活函数sigmoid,tanh和relu,关于激活函数详细的描述,可以参考这里: 详解激活函数(Sigmoid/Tanh/ReLU/Leaky ReLu等) - 知乎 import tensorflow as tf import numpy as nptf.__ve…...
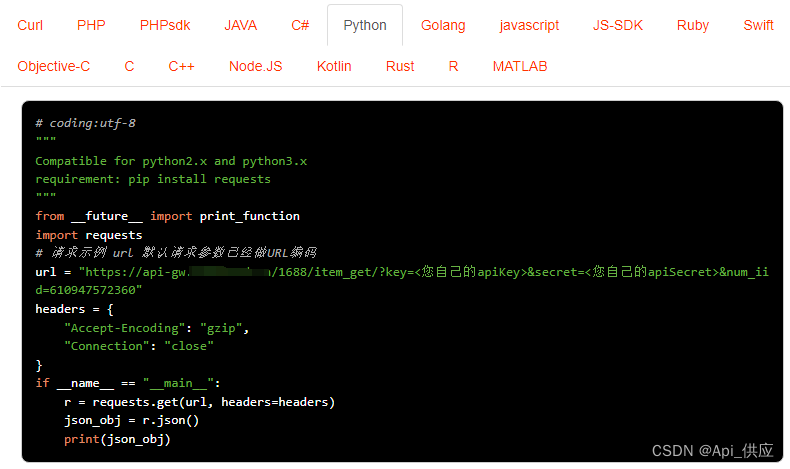
1688商品详情数据采集,工程数据采集丨店铺数据采集丨商品详情数据采集
1688是中国的一个大型B2B电子商务平台,主要用于批发和采购各种商品。对于需要从1688上获取商品详情数据、工程数据或店铺数据的用户来说,可以采用以下几种常见的方法: 官方API接口:如果1688提供了官方的API接口,那么可…...

Flutter(四):SingleChildScrollView、GridView
SingleChildScrollView、GridView 遇到的问题 以下代码会报错: class GridViewPage extends StatefulWidget {const GridViewPage({super.key});overrideState<GridViewPage> createState() > _GridViewPage(); }class _GridViewPage extends State<GridViewPage&g…...

【C++】102.二叉树的层序遍历
题目描述 给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。 示例1: 输入:root [3,9,20,null,null,15,7] 输出:[[3],[9,20],[15,7]]示例 2࿱…...

Java学习笔记006——子类与父类的类型转换
在Java中,类型转换主要涉及到两种类型:向上类型转换(Upcasting)和向下类型转换(Downcasting)。 1. 向上类型转换(Upcasting): 向上类型转换是将子类的对象转换为父类类…...

FedAsync Asynchronous Federated Optimization
文章目录 IntroductionMethodologyConvergence analysisExperiments Introduction 联邦学习有三个关键属性: 不频繁的任务激活。对于弱边缘设备,学习任务只在设备空闲、充电、连接非计量网络时执行.沟通不频繁。边缘设备和远程服务器之间的连接可能经常不可用、缓…...

学习基于 JavaScript 语言 的计算机界三大神书”之一 ——SICP
如何阅读“计算机界三大神书”之一 ——SICP 《计算机程序的构造和解释》(Structure and Interpretation of Computer Programs,简记为SICP)是MIT的基础课教材,出版后引起计算机教育界的广泛关注,对推动全世界大学计算…...

【RISC-V 指令集】RISC-V 向量V扩展指令集介绍(一)-向量扩展编程模型
1. 引言 以下是《riscv-v-spec-1.0.pdf》文档的关键内容: 这是一份关于向量扩展的详细技术文档,内容覆盖了向量指令集的多个关键方面,如向量寄存器状态映射、向量指令格式、向量加载和存储操作、向量内存对齐约束、向量内存一致性模型、向量…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...
