当前位置： 首页 > news >正文

Matlab梁单元有限元编程 | 铁木辛柯梁 | 欧拉梁 | Matlab源码 | 理论文本

news 文章来源：https://blog.csdn.net/u010542847/article/details/136512309 2025/5/10 7:08:17

专栏导读

  • 作者简介：工学博士，高级工程师，专注于工业软件算法研究
  • 本文已收录于专栏：《有限元编程从入门到精通》本专栏旨在提供 1.以案例的形式讲解各类有限元问题的程序实现，并提供所有案例完整源码；2.单元类型包含：杆单元，梁单元，平面三角形单元，薄板单元，厚板单元，壳单元，四/六面体实体单元，金字塔单元等；3.物理场问题涉及：力学、传热学、电磁学及多物理场耦合等问题的稳态（静力学）和瞬态（动力学）求解。专栏旨在帮助有志于有限元工业软件开发的小伙伴，快速上手有限元编程，在案例中成长，摆脱按部就班填鸭式教学。
  • 【所有专栏文章均提供对应视频课】，文本教程+视频教程，双向强化学习！
  • 欢迎订阅专栏，订阅用户可私聊进入有限元编程交流群（知识交流、问题解答），并获赠丰厚的有限元相关学习资料（教材、源码、视频课）
  • 专栏订阅地址：有限元编程从入门到精通_suoge223的博客-CSDN博客

文章目录

专栏导读

文章目录

【总体简介】💻🔍

【代码截图】

【理论文本截图】

【视频教程】

【总体简介】💻🔍

本代码实现了二维悬臂梁结构的matlab有限元编程，涉及的梁单元类型有欧拉梁单元和铁木辛柯梁单元，实现上述两类梁单元静力分析求解，并针对铁木辛柯梁单元剪切自锁问题，开发了两种铁木辛柯梁单元，一种为完全积分的铁木辛柯梁，一种是减缩积分的铁木辛柯梁，并且对比了欧拉梁、铁木辛柯梁（完全积分）、铁木辛柯梁（减缩积分）的计算结果。

你将获得： 欧拉梁vs铁木辛柯梁matlab源码 + 理论文本

获取地址：Matlab梁单元有限元编程 | 铁木辛柯梁 | 欧拉梁 | Matlab源码 | 理论文本

代码运行的结果如下：

（1）L=5000,H=700,B=300的梁的计算结果

（2）L=5000,H=2700,B=300的梁的计算结果

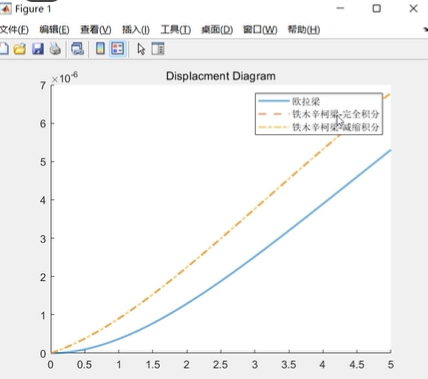
（3）L=5000,H=7,B=300的梁的计算结果

可见，对于（1）所示以弯曲变形为主的梁结构，三种单元均能给出一个较为准确的结果；对于（2）所示的深梁，剪切变形不可忽略，导致欧拉梁与铁木辛柯梁的计算结果相差较大，而且两种铁木辛柯梁均给出较精确的结果；对于（3）所示的扁梁，以受弯变形为主，因此欧拉梁和减缩积分的铁木辛柯梁均能给出合理结果，但是由于完全积分的铁木辛柯梁会发生严重的剪切自锁现象，因此与欧拉梁和减缩积分的铁木辛柯梁的结果相差较大。

【代码截图】

【理论文本截图】

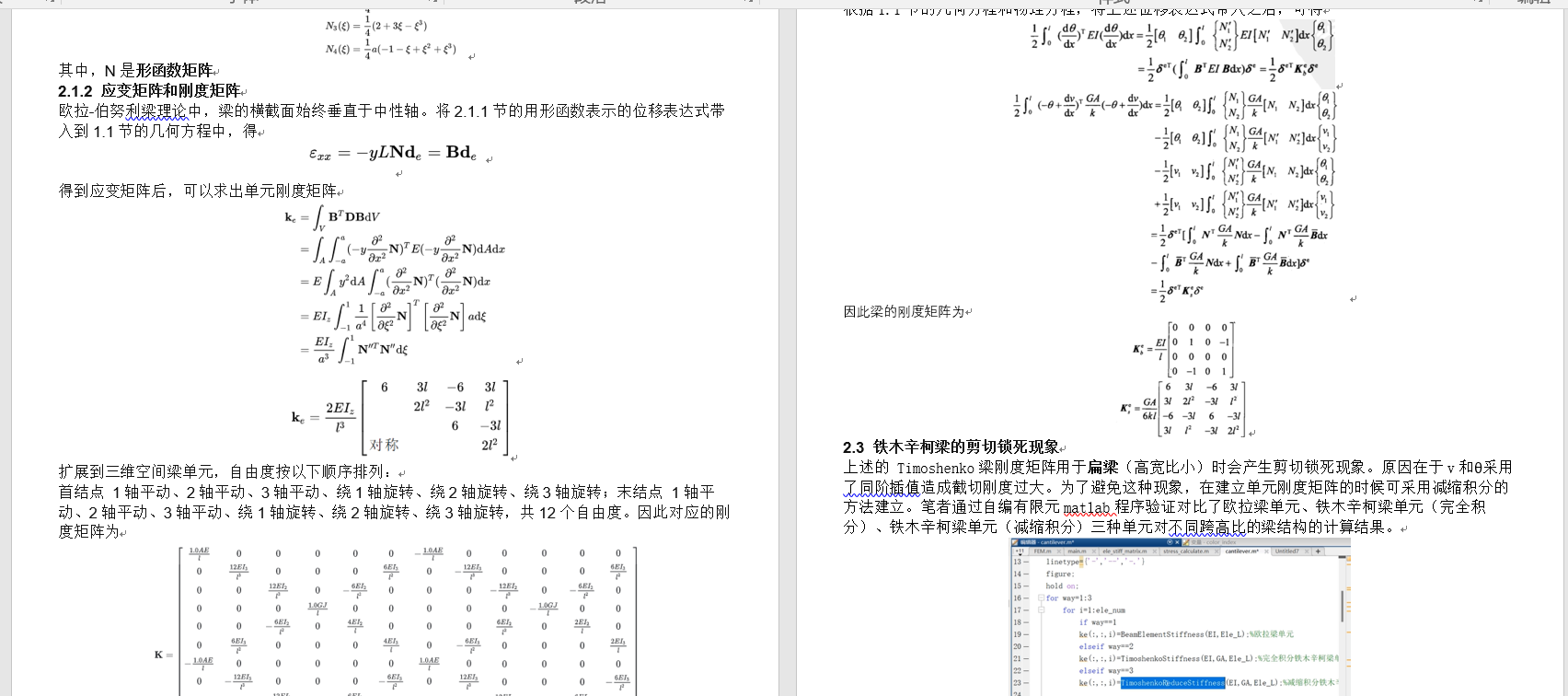
【视频教程】

【Matlab有限元编程从入门到精通/后处理/刚度矩阵/等参单元/高斯积分/Hammer积分/非线性/静力/动力/传热/三维/二维/梁板壳/实体/平面】 Matlab有限元编程从入门到精通/后处理/刚度矩阵/等参单元/高斯积分/Hammer积分/非线性/静力/动力/传热/三维/二维/梁板壳/实体/平面_哔哩哔哩_bilibili

相关文章：

Matlab梁单元有限元编程 | 铁木辛柯梁 | 欧拉梁 | Matlab源码 | 理论文本

专栏导读 作者简介：工学博士，高级工程师，专注于工业软件算法研究本文已收录于专栏：《有限元编程从入门到精通》本专栏旨在提供 1.以案例的形式讲解各类有限元问题的程序实现，并提供所有案例完整源码；2.单元…...

编程日记 2024/3/7 6:05:59

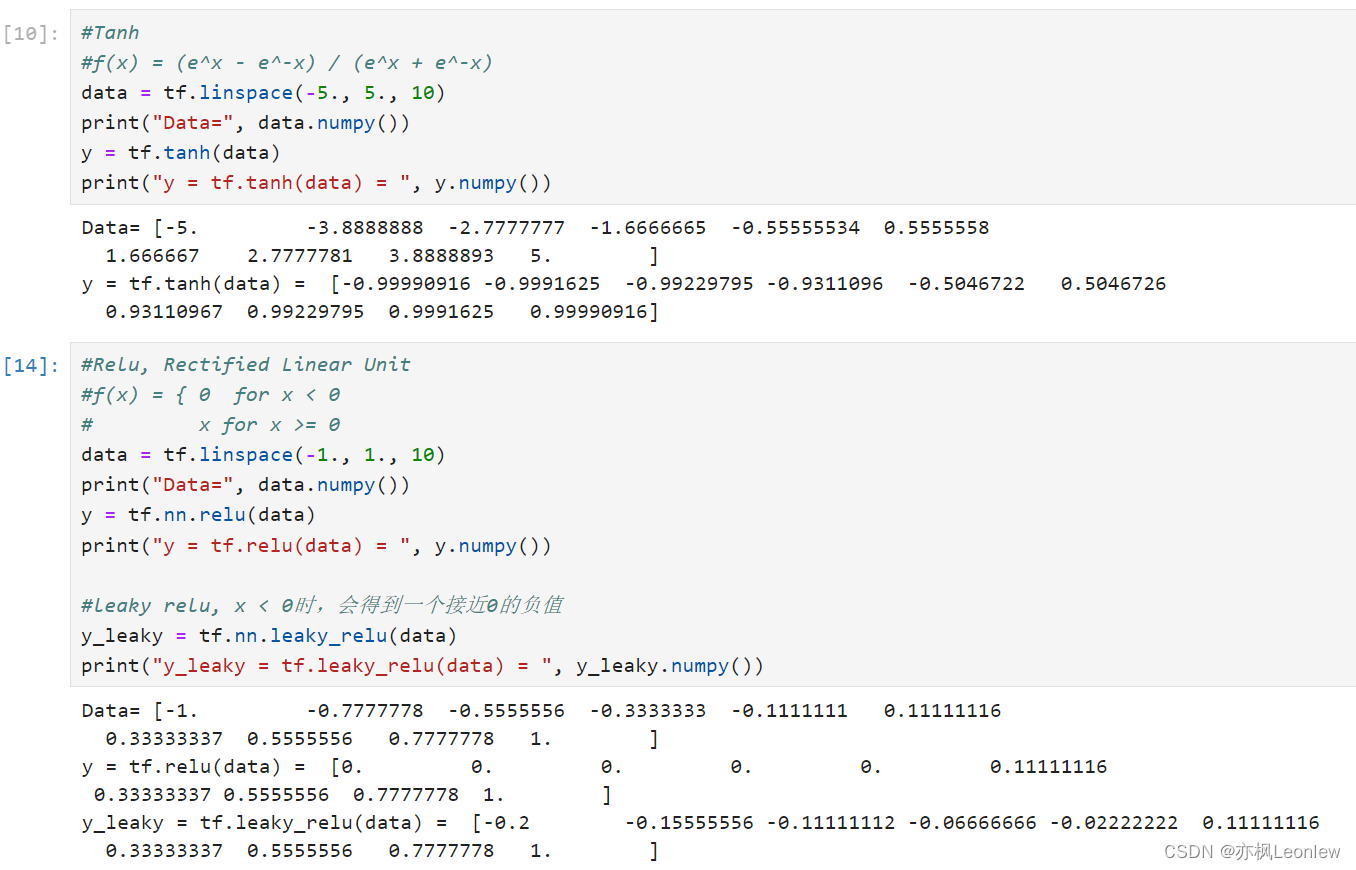
Tensorflow2.0笔记 - 常见激活函数sigmoid，tanh和relu

本笔记主要记录常见的三个激活函数sigmoid，tanh和relu，关于激活函数详细的描述，可以参考这里： 详解激活函数（Sigmoid/Tanh/ReLU/Leaky ReLu等） - 知乎 import tensorflow as tf import numpy as nptf.__ve…...

编程日记 2024/3/7 6:03:57

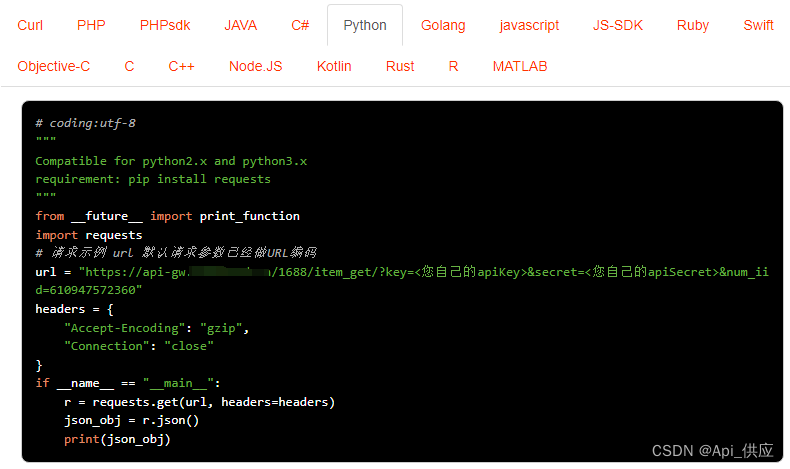
1688商品详情数据采集，工程数据采集丨店铺数据采集丨商品详情数据采集

1688是中国的一个大型B2B电子商务平台，主要用于批发和采购各种商品。对于需要从1688上获取商品详情数据、工程数据或店铺数据的用户来说，可以采用以下几种常见的方法： 官方API接口：如果1688提供了官方的API接口，那么可…...

编程日记 2024/3/7 6:02:56

Flutter（四）：SingleChildScrollView、GridView

SingleChildScrollView、GridView 遇到的问题 以下代码会报错: class GridViewPage extends StatefulWidget {const GridViewPage({super.key});overrideState<GridViewPage> createState() > _GridViewPage(); }class _GridViewPage extends State<GridViewPage&g…...

编程日记 2024/3/7 5:59:53

【C++】102.二叉树的层序遍历

题目描述 给你二叉树的根节点 root &#xff0c;返回其节点值的 层序遍历 。 &#xff08;即逐层地&#xff0c;从左到右访问所有节点&#xff09;。 示例1&#xff1a; 输入&#xff1a;root [3,9,20,null,null,15,7] 输出&#xff1a;[[3],[9,20],[15,7]]示例 2&#xff1…...

编程日记 2024/3/7 5:58:52

Java学习笔记006——子类与父类的类型转换

在Java中&#xff0c;类型转换主要涉及到两种类型&#xff1a;向上类型转换&#xff08;Upcasting&#xff09;和向下类型转换&#xff08;Downcasting&#xff09;。 1. 向上类型转换&#xff08;Upcasting&#xff09;&#xff1a; 向上类型转换是将子类的对象转换为父类类…...

编程日记 2024/3/7 5:57:51

FedAsync Asynchronous Federated Optimization

文章目录 IntroductionMethodologyConvergence analysisExperiments Introduction 联邦学习有三个关键属性: 不频繁的任务激活。对于弱边缘设备&#xff0c;学习任务只在设备空闲、充电、连接非计量网络时执行.沟通不频繁。边缘设备和远程服务器之间的连接可能经常不可用、缓…...

编程日记 2024/3/7 5:56:50

学习基于 JavaScript 语言 的计算机界三大神书”之一 ——SICP

如何阅读“计算机界三大神书”之一 ——SICP 《计算机程序的构造和解释》&#xff08;Structure and Interpretation of Computer Programs&#xff0c;简记为SICP&#xff09;是MIT的基础课教材&#xff0c;出版后引起计算机教育界的广泛关注&#xff0c;对推动全世界大学计算…...

编程日记 2024/3/7 5:55:49

【RISC-V 指令集】RISC-V 向量V扩展指令集介绍(一)-向量扩展编程模型

1. 引言 以下是《riscv-v-spec-1.0.pdf》文档的关键内容&#xff1a; 这是一份关于向量扩展的详细技术文档&#xff0c;内容覆盖了向量指令集的多个关键方面&#xff0c;如向量寄存器状态映射、向量指令格式、向量加载和存储操作、向量内存对齐约束、向量内存一致性模型、向量…...

编程日记 2024/3/7 5:54:49

K8s 镜像缓存管理 kube-fledged 认知

写在前面 博文内容为K8s 镜像缓存管理 kube-fledged 认知内容涉及&#xff1a; kube-fledged 简单介绍部署以及基本使用 理解不足小伙伴帮忙指正 不必太纠结于当下&#xff0c;也不必太忧虑未来&#xff0c;当你经历过一些事情的时候&#xff0c;眼前的风景已经和从前不一样了。…...

编程日记 2024/3/7 5:52:45

ModbusTcp协议

Modbus TCP是一种通信协议&#xff0c;用于工业设备之间的通信。它是Modbus协议家族中的一个成员&#xff0c;最初是为串行通信设计的&#xff0c;但后来扩展到了TCP/IP网络。Modbus TCP/IP是一种公开的标准&#xff0c;由Modbus组织制定&#xff0c;并且被广泛应用于工业自动化…...

编程日记 2024/3/7 5:48:42

常用工具——Gradle

前言 实践是最好的学习方式&#xff0c;技术也如此。 文章目录 前言一、Gradle 简介二、文件结构详解 一、Gradle 简介 Gradle 文件是一个独立于 android 之外的一个东西&#xff1b; 是什么 gradle 就是编译、打包 Android 工程的一个构建工具&#xff1b;build.gradle 文件&…...

编程日记 2024/3/7 5:47:41

OpenHarmony教程指南—Navigation开发 页面切换场景范例

简介 在应用开发时&#xff0c;我们常常遇到&#xff0c;需要在应用内多页面跳转场景时中使用Navigation导航组件做统一的页面跳转管理&#xff0c;它提供了一系列属性方法来设置页面的标题栏、工具栏以及菜单栏的各种展示样式。除此之外还拥有动态加载&#xff0c;navPathSta…...

编程日记 2024/3/7 5:46:40

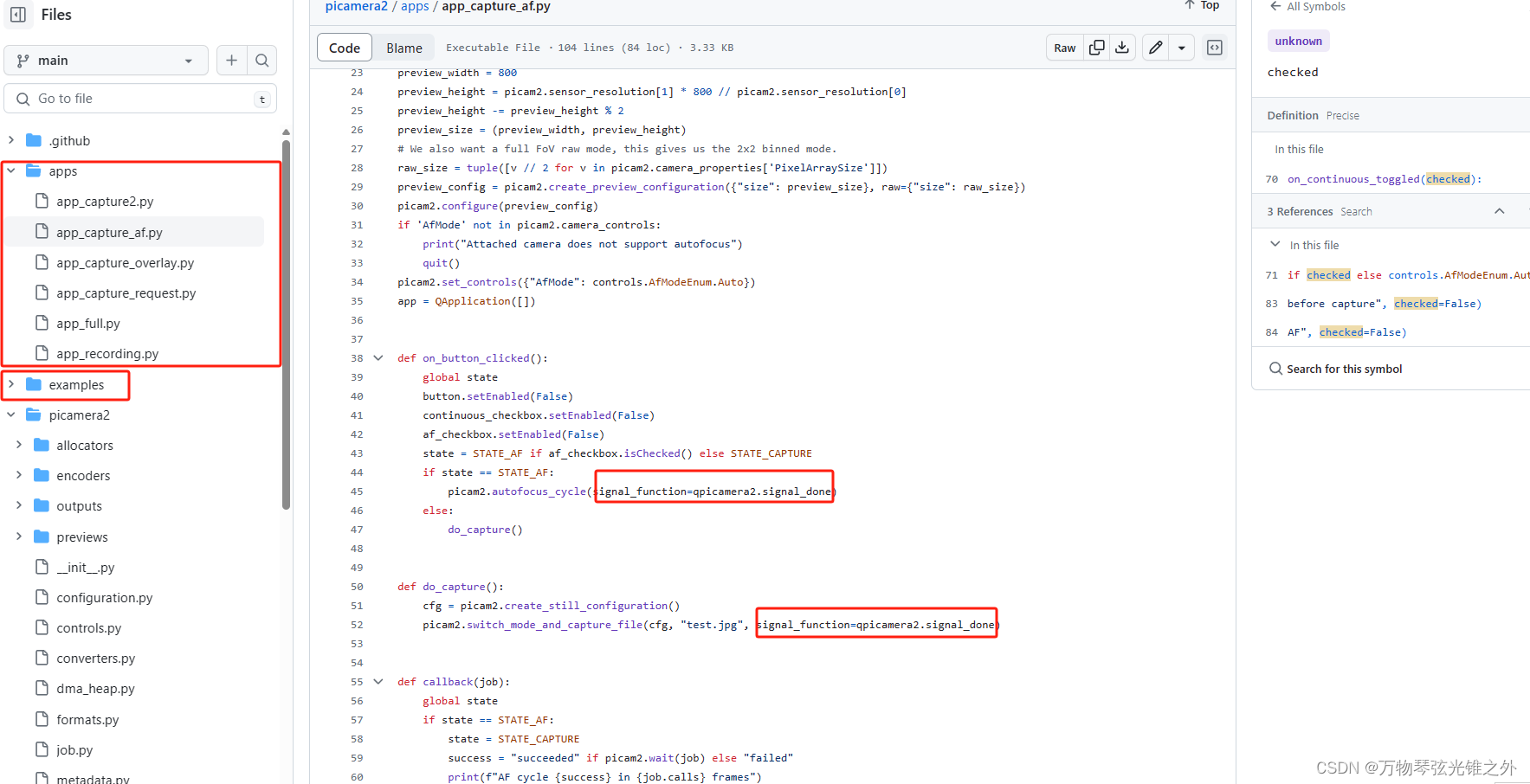
2024-简单点-picamera2除了文档还有哪里可以学习实例？

picamera2学习例子 去github的picamera2库&#xff0c;找app和examples目录&#xff0c;然后学习...

编程日记 2024/3/7 5:42:36

JavaScript实现点击鼠标弹钢琴的效果

思路&#xff1a; 图片设置宽900px&#xff0c;找到鼠标按下时的x坐标和img距离body的x坐标&#xff0c;两个值相减&#xff0c;然后除100取整&#xff0c;赋值给a&#xff0c;通过判断a的值来确定放出那个音乐。 完整代码&#xff1a; <!DOCTYPE html> <html lan…...

编程日记 2024/3/7 5:40:34

docker-compose Install rustdesk

RustDesk RustDesk 是一款开源的远程支持和远程桌面工具，它旨在为用户提供便捷的远程协助和远程访问功能。 默认情况下，hbbs 监听21115(tcp), 21116(tcp/udp), 21118(tcp)，hbbr 监听21117(tcp), 21119(tcp)。务必在防火墙开启这几个端口， 请注意21116同时要开启TCP和UDP。…...

编程日记 2024/3/7 5:38:32

初学C++

注释 变量 作用&#xff1a;给一段指定的内存空间起名&#xff0c;方便操作这段内容 数据类型 变量名 变量初始值; 常量 用于记录程序中不可更改的数据 宏常量&#xff1a; #define 宏常量 常量值 const修饰的变量&#xff1a; const 数据类型 常量名 常量值; 关键字 …...

编程日记 2024/3/7 5:37:31

数据分析-Pandas数据y轴双坐标设置

数据分析-Pandas数据y轴双坐标设置 数据分析和处理中&#xff0c;难免会遇到各种数据&#xff0c;那么数据呈现怎样的规律呢&#xff1f;不管金融数据&#xff0c;风控数据&#xff0c;营销数据等等&#xff0c;莫不如此。如何通过图示展示数据的规律&#xff1f; 数据表&…...

编程日记 2024/3/7 5:34:27

Android多线程实现方式及并发与同步，Android面试题汇总

一. 开发背景 想要成为一名优秀的Android开发&#xff0c;你需要一份完备的知识体系&#xff0c;在这里&#xff0c;让我们一起成长为自己所想的那样。 我们的项目需要开发一款智能硬件。它由 Web 后台发送指令到一款桌面端应用程序&#xff0c;再由桌面程序来控制不同的硬件设…...

编程日记 2024/3/7 5:33:26

2023年全国职业院校技能大赛中职组大数据应用与服务赛项题库参考答案陆续更新中，敬请期待…

2023年全国职业院校技能大赛中职组大数据应用与服务赛项题库参考答案陆续更新中&#xff0c;敬请期待… 武汉唯众智创科技有限公司 2024 年 2 月 联系人&#xff1a;辜渝傧13037102709 题号&#xff1a;试题01 模块三&#xff1a;业务分析与可视化 &#xff08;一&#xff0…...

编程日记 2024/3/7 5:31:22

设计MySQL数据表的几个注意点

最近合作搞项目&#xff0c;发现了很多问题。特别的&#xff0c;数据库层面上的问题更为致命。记录一下&#xff0c;希望后面看到博客的同学们注意。 注意&#xff1a;以下观点只用于一般情况下的单体、微服务&#xff0c;不保证适用所有场景。 一、ID问题 ID名称问题 如下图…...

编程日记 2024/3/7 5:30:22

android 键盘遮挡输入框问题回忆

背景 刚开始做Android的时候&#xff0c;有一次遇到输入框位于页面底部&#xff0c;弹出的键盘老是遮挡输入框&#xff0c;这就给人一种感觉----不咋舒服。当时&#xff0c;网上百度了一遍&#xff0c;后面终于解决了&#xff0c;由于当时天天加班&#xff0c;没时间写博客&…...

编程日记 2024/3/7 5:29:21

ZJGSU 1737 链表

题目描述 请根据输入数据构造一个带头结点的单链表&#xff0c;链表结点的数据结构为struct node {int data; struct node *next;}&#xff0c;试设计算法&#xff1a;按递增次序输出单链表中各结点的数据元素&#xff0c;并释放结点所占用的存储空间。 要求&#xff1a;不允…...

编程日记 2024/3/7 5:26:18

Java开发人员不得不收集的代码，java软件开发面试常见问题

前言 今年的金三银四已经过去一大半了&#xff0c;在这其中参与过不少面试&#xff0c;2021都说工作不好找&#xff0c;这也是对开发人员的要求变向的提高了。 之前在Github上收获15Kstar的Java核心神技&#xff08;这参数&#xff0c;质量多高就不用我多说了吧&#xff09;非…...

编程日记 2024/3/7 5:25:17

浅谈块存储、文件存储、对象存储

**块存储、文件存储和对象存储各自有其独特的特点和适用场景**。具体来说&#xff1a; 1. **块存储**&#xff1a; - 描述&#xff1a;块存储将存储空间分割成固定大小的块&#xff0c;这些块可以直接映射到主机操作系统。它提供的是原始的存储空间&#xff0c;不带文件系统…...

编程日记 2024/3/7 5:22:14

2024年 Python面试热点

当然&#xff0c;以下是一些Python相关的热点面试题&#xff1a; 请解释一下Python中的装饰器&#xff08;Decorators&#xff09;是什么&#xff0c;以及它们的主要用途是什么&#xff1f; 装饰器是Python中的一个高级功能&#xff0c;它允许用户修改或增强函数、方法或类的行…...

编程日记 2024/3/7 5:18:09

Map集合体系——遍历，HashMap，TreeMap，LikedHashMap

认识Map集合 Map集合体系特点 方法 代码示例 package com.zz.Map;import java.util.*;public class Test {public static void main(String args[]){Map<String, Integer> map new HashMap <>();//经典代码&#xff0c;按照键 无序 不重复 无索引map.put("…...

编程日记 2024/3/7 5:13:05

docker mysql主从复制

新建主服务器容器实例3301 mysql 主 3301 docker run -p 3301:3306 --name mysql-master \ -v /mydata/mysql-master/log:/var/log/mysql \ -v /mydata/mysql-master/data:/var/lib/mysql \ -v /mydata/mysql-master/conf:/etc/mysql \ -v /home/mysql/mysql-files:/var/lib/…...

编程日记 2024/3/7 5:12:04

iOS 自动化测试踩坑(一): 技术方案、环境配置与落地实践

移动端的自动化测试&#xff0c;最常见的是 Android 自动化测试&#xff0c;我个人觉得 Android 的测试优先级会更高&#xff0c;也更开放&#xff0c;更容易测试&#xff1b;而 iOS 相较于 Android 要安全稳定的多&#xff0c;但也是一个必须测试的方向&#xff0c;这个系列文…...

编程日记 2024/3/7 5:11:03

Redis的事务

在 Redis 中&#xff0c;事务&#xff08;Transaction&#xff09;是一组命令的集合&#xff0c;可以作为一个单独的操作来执行&#xff0c;保证这组命令要么全部执行成功&#xff0c;要么全部执行失败&#xff0c;具有原子性。在 Redis 中&#xff0c;事务是通过 MULTI、EXEC、…...

编程日记 2024/3/7 5:10:02