01 LM 算法及 Cpp 实现
文章目录
- 01 LM 算法及 Cpp 实现
- 1.1 应用
- 1.2 阻尼法推导
- 1.3 Cpp 算法实现
01 LM 算法及 Cpp 实现
1.1 应用
LM 算法用于解决非线性最小二乘问题
min x F ( x ) = 1 2 ∥ f ( x ) ∥ 2 2 (1) \min _x F(x)=\frac{1}{2}\|f(\boldsymbol{x})\|_2^2 \tag{1} xminF(x)=21∥f(x)∥22(1)
其中, f ( x ) f(\boldsymbol{x}) f(x) 是指各项的残差。
LM 算法有两种推导方式,即 阻尼法 和 置信域 法(见《十四讲》),这里用阻尼法进行推导。
1.2 阻尼法推导
(1)一阶泰勒展开近似
将 f ( x ) f(\boldsymbol{x}) f(x) 在 x n \boldsymbol{x_n} xn 处一阶泰勒展开(把 Δ x \Delta \boldsymbol{x} Δx 看做未知数),
f ( x n + Δ x ) ≈ f ( x n ) + J ( x n ) Δ x (2) f(\boldsymbol{x_n}+\Delta \boldsymbol{x}) \approx f(\boldsymbol{x_n})+\boldsymbol{J}\left(\boldsymbol{x}_n\right) \Delta \boldsymbol{x} \tag{2} f(xn+Δx)≈f(xn)+J(xn)Δx(2)
那么问题转化为,对于每次迭代,求解最优的 Δ x \Delta \boldsymbol{x} Δx 。
Δ x ∗ = arg min Δ x 1 2 ∥ f ( x n ) + J n ( x n ) Δ x ∥ 2 (3) \Delta \boldsymbol{x}^*=\arg \min _{\Delta \boldsymbol{x}} \frac{1}{2}\left\|f\left(\boldsymbol{x}_{\boldsymbol{n}}\right)+\boldsymbol{J}_{\boldsymbol{n}}\left(\boldsymbol{x}_{\boldsymbol{n}}\right) \Delta \boldsymbol{x}\right\|^2 \tag{3} Δx∗=argΔxmin21∥f(xn)+Jn(xn)Δx∥2(3)
(2)加入阻尼项
Δ x ∗ = arg min Δ x M ( Δ x ) = 1 2 ∥ f ( x n ) + J n ( x n ) Δ x ∥ 2 + 1 2 μ Δ x T Δ x (4) \Delta \boldsymbol{x}^*=\arg \min _{\Delta \boldsymbol{x}} M(\Delta \boldsymbol{x})=\frac{1}{2}\left\|f\left(\boldsymbol{x}_{\boldsymbol{n}}\right)+\boldsymbol{J}_{\boldsymbol{n}}\left(\boldsymbol{x}_{\boldsymbol{n}}\right) \Delta \boldsymbol{x}\right\|^2+\frac{1}{2} \mu \Delta \boldsymbol{x}^T \Delta \boldsymbol{x} \tag{4} Δx∗=argΔxminM(Δx)=21∥f(xn)+Jn(xn)Δx∥2+21μΔxTΔx(4)
其中, μ \mu μ 为阻尼系数,阻尼项 1 2 μ Δ x T Δ x \frac{1}{2} \mu \Delta \boldsymbol{x}^T \Delta \boldsymbol{x} 21μΔxTΔx 可以看做是对于过大的 Δ x \Delta \boldsymbol{x} Δx 的惩罚。
(3)求极值
对 Δ x \Delta \boldsymbol{x} Δx 求导,并令其等于零,
J ( x n ) T f ( x n ) + J ( x n ) T J ( x n ) Δ x + μ Δ x = 0 (5) \boldsymbol{J}\left(\boldsymbol{x}_{\boldsymbol{n}}\right)^T f\left(\boldsymbol{x}_{\boldsymbol{n}}\right)+\boldsymbol{J}\left(\boldsymbol{x}_{\boldsymbol{n}}\right)^T \boldsymbol{J}\left(\boldsymbol{x}_{\boldsymbol{n}}\right) \Delta \boldsymbol{x}+\mu \Delta \boldsymbol{x}=\mathbf{0} \tag{5} J(xn)Tf(xn)+J(xn)TJ(xn)Δx+μΔx=0(5)
得
Δ x ∗ = − ( J ( x n ) T J ( x n ) + μ I ) − 1 J ( x n ) T f ( x n ) (6) \Delta \boldsymbol{x}^*=-\left(\boldsymbol{J}\left(\boldsymbol{x}_{\boldsymbol{n}}\right)^T \boldsymbol{J}\left(\boldsymbol{x}_{\boldsymbol{n}}\right)+\mu \boldsymbol{I}\right)^{-1} \boldsymbol{J}\left(\boldsymbol{x}_{\boldsymbol{n}}\right)^T f\left(\boldsymbol{x}_{\boldsymbol{n}}\right) \tag{6} Δx∗=−(J(xn)TJ(xn)+μI)−1J(xn)Tf(xn)(6)
令
J ( x n ) T J ( x n ) = H J ( x n ) T f ( x n ) = g \begin{aligned} \boldsymbol{J}\left(\boldsymbol{x}_{\boldsymbol{n}}\right)^T \boldsymbol{J}\left(\boldsymbol{x}_{\boldsymbol{n}}\right) &=\boldsymbol{H} \\ \boldsymbol{J}\left(\boldsymbol{x}_{\boldsymbol{n}}\right)^T f\left(\boldsymbol{x}_{\boldsymbol{n}}\right) &=\boldsymbol{g} \end{aligned} J(xn)TJ(xn)J(xn)Tf(xn)=H=g
则式(6)可写为
Δ x ∗ = − ( H + μ I ) − 1 g (7) \Delta \boldsymbol{x}^*=-(\boldsymbol{H}+\mu \boldsymbol{I})^{-1} \boldsymbol{g} \tag{7} Δx∗=−(H+μI)−1g(7)
(4)阻尼系数 μ \mu μ 的调节
定义增益系数 ρ \rho ρ
ρ = f ( x + Δ x ) − f ( x ) J ( x ) T Δ x (8) \rho=\frac{f(\boldsymbol{x}+\boldsymbol{\Delta x})-f(\boldsymbol{x})}{\boldsymbol{J}(\boldsymbol{x})^T\Delta \boldsymbol{x}} \tag{8} ρ=J(x)TΔxf(x+Δx)−f(x)(8)
其中,分子是实际下降的值,分母是近似下降的值。若 ρ \rho ρ 接近于 1 ,则近似效果好;若 ρ \rho ρ 太小,则说明实际减小的值远小于近似减小的值,即近似效果较差,需缩小近似范围,即增大阻尼系数 μ \mu μ; 若 ρ \rho ρ 太大,则说明实际减小的值大于近似减小的值,则需放大近似范围,即减小 μ \mu μ。
两种调节方法:
if ρ < 0.25 μ : = μ ∗ 2 else if ρ > 0.75 μ : = μ / 3 \begin{aligned} \text { if } & \rho<0.25 \\ & \mu:=\mu * 2 \\ \text { else if } & \rho>0.75 \\ & \mu:=\mu / 3 \end{aligned} if else if ρ<0.25μ:=μ∗2ρ>0.75μ:=μ/3
也就是, ρ < 0.25 \rho<0.25 ρ<0.25 时增大阻尼系数; ρ > 0.75 \rho>0.75 ρ>0.75 时,减小阻尼系数。
或者:
i f ρ > 0 μ : = μ ∗ max { 1 3 , 1 − ( 2 ρ − 1 ) 3 } ; ν : = 2 e l s e μ : = μ ∗ ν ; ν : = 2 ∗ ν \begin{aligned} if \rho>0 \\ &\mu:=\mu * \max \left\{\frac{1}{3}, 1-(2 \rho-1)^3\right\} ; \quad \nu:=2\\ else\\ &\mu:=\mu * \nu ; \quad \nu:=2 * \nu \end{aligned} ifρ>0elseμ:=μ∗max{31,1−(2ρ−1)3};ν:=2μ:=μ∗ν;ν:=2∗ν
1.3 Cpp 算法实现
两种方法差别在于 ρ \rho ρ 的分母的计算(我的更快?)。
优化目标是待定系数,把他们看做 未知数,需要计算的 step 就是这些待定系数的 step。
(1)我的方法
/*********************************************************** *
* Time: 2022/11/3
* Author: xiaocong
* Function: LM 算法** @ 解决的是最小二乘问题,也就是找到最优的系数使得残差最小* @ obj = A * sin(Bx) + C * cos(D*x) - F* A * sin(Bx) + C * cos(D*x) 是目标函数* F 是实际值* 目标是找到使 obj 最小的系数 A B C D
***********************************************************/#include <Eigen/Dense> // 稠密矩阵
#include <Eigen/Sparse> // 稀疏矩阵
#include <iostream>
#include <cmath>using namespace std;
using namespace Eigen;const double DERIV_STEP = 1e-5;
const int MAX_INTER = 100;#define max(a, b) (((a)>(b))?(a):(b))// 定义目标函数
double func(const VectorXd input, const VectorXd &output, const VectorXd ¶ms, int objIndex)
{// obj = A * sin(Bx) + C * cos(D*x) - Fdouble x1 = params(0); // params 中存储的是系数double x2 = params(1);double x3 = params(2);double x4 = params(3);double t = input(objIndex); // input 中存储的是 xdouble f = output(objIndex); // output 中存储的是实际值return x1 * sin(x2 * t) + x3 * cos(x4 * t) - f; // 返回 objIndex 项的残差
}// 计算残差矩阵
VectorXd objF(const VectorXd &input, const VectorXd &output, const VectorXd ¶ms)
{VectorXd obj(input.rows()); // 存储所有残差,也就是残差矩阵for (int i = 0; i < input.rows(); i++)obj(i) = func(input, output, params, i);return obj; // 返回残差矩阵
}// 残差平方和
double Func(const VectorXd &obj)
{return obj.squaredNorm() / 2.0;
}// 求某个系数在某点的导数
double Deriv(const VectorXd &input, const VectorXd &output, int objIndex, const VectorXd ¶ms, int paraIndex)
{VectorXd para1 = params;VectorXd para2 = params;para1(paraIndex) -= DERIV_STEP;para2(paraIndex) += DERIV_STEP;double obj1 = func(input, output, para1, objIndex);double obj2 = func(input, output, para2, objIndex);return (obj2 - obj1) / (2 * DERIV_STEP); // 该点处的导数,为求雅克比矩阵做准备
}// 计算雅克比矩阵
/***************************** 我们优化的是系数 params,把他们看做未知数,分别求导,得到雅克比矩阵* 维度:(input.rows() x params.rows())* [[df/dA df/dB df/dC df/dD] <--- x1* [df/dA df/dB df/dC df/dD] <--- x2* [.......................]* [df/dA df/dB df/dC df/dD]] <--- xn****************************/
MatrixXd Jacobian(const VectorXd &input, const VectorXd &output, const VectorXd ¶ms)
{int rowNum = input.rows();int colNum = params.rows();MatrixXd Jac(rowNum, colNum);for (int i = 0; i < rowNum; i++)for (int j = 0; j < colNum; j++)Jac(i, j) = Deriv(input, output, i, params, j);return Jac;
}//求 Hessian 矩阵对角线最大值
// Hessian 矩阵:二阶导数
double maxMatrixDiagonale(const MatrixXd &Hessian)
{int max = 0;for (int i = 0; i < Hessian.rows(); i++){if(Hessian(i, i) > max)max = Hessian(i, i);}return max;
}// 近似下降值
double linerDeltaL(const VectorXd &step, const MatrixXd &Jac)
{VectorXd L = Jac * step;return L.norm();
}void levenMar(const VectorXd &input, const VectorXd &output, VectorXd ¶ms)
{double epsilon = 1e-12;int iterCnt = 0; // 迭代计数double tao = 1e-3;long long v = 2;// 求初始的 uMatrixXd Jac = Jacobian(input, output, params); // 得到雅克比矩阵MatrixXd H = Jac.transpose() * Jac; // 得到 Hessian 矩阵,4x4double u = tao * maxMatrixDiagonale(H); // Hessian 矩阵对角线最大值乘 taowhile (iterCnt < MAX_INTER) // double 类型不能直接作比较{VectorXd obj = objF(input, output, params); // 误差矩阵MatrixXd Jac = Jacobian(input, output, params); // 得到雅克比矩阵MatrixXd H = Jac.transpose() * Jac; // 得到 Hessian 矩阵,4x4VectorXd g = Jac.transpose() * obj; // 也就是 g,4x1VectorXd step = (H + u * MatrixXd::Identity(H.rows(), H.cols())).inverse() * g;if(step.norm() < epsilon)break;cout << "H:" << endl << H << endl;cout << "step: " << endl << step << endl;VectorXd paramsNew(params.rows());paramsNew = params - step; // 更新 params// 计算 params 误差obj = objF(input, output, params);// 计算 paramsNew 误差VectorXd obj_new = objF(input, output, paramsNew);double deltaF = Func(obj) - Func(obj_new); // 求差double deltaL = linerDeltaL(step, Jac);// 计算增益系数 rhodouble rho = deltaF / deltaL; // 实际下降值 / 近似下降值cout << "rho is; " << rho <<endl;if(rho > 0){params = paramsNew;u *= max(1.0 / 3.0, 1 - pow(2 * rho - 1, 3));v = 2;} else{u = u * v;v = v * 2;}cout << "u= " << u << "\tv= " << v << endl;iterCnt ++;cout << "Iteration " << iterCnt << " times, result is :" << endl<< params << endl;}
}int main()
{int params_num = 4;int total_data = 100;VectorXd input(total_data);VectorXd output(total_data);double A = 5, B = 1, C = 10, D = 2; // 初始化// 生成数据for (int i = 0; i < total_data; i++){double x = 20.0 * ((rand() % 1000) / 1000.0) - 10.0; // [-10, 10]double deltaY = 2.0 * (rand() % 1000) / 1000.0; // 随机噪声,[0, 2]double y = A * sin(B*x) + C * cos(D*x) + deltaY;input(i) = x;output(i) = y;}VectorXd params_levenMar(params_num);params_levenMar << 3.6, 1.3, 7.2, 1.7;levenMar(input, output, params_levenMar);cout << "**********************************************" << endl;cout << "Levenberg-Marquardt parameter: " << endl << params_levenMar << endl;}
输出
Levenberg-Marquardt parameter:4.85628
0.99790410.05242.003
(2)网络方法
/*********************************************************** *
* Time: 2022/11/2
* Author: xiaocong
* Function: LM 算法** @ 解决的是最小二乘问题,也就是找到最优的系数使得残差最小* @ obj = A * sin(Bx) + C * cos(D*x) - F* A * sin(Bx) + C * cos(D*x) 是目标函数* F 是实际值* 目标是找到使 obj 最小的系数 A B C D
***********************************************************/#include <Eigen/Dense> // 稠密矩阵
#include <Eigen/Sparse> // 稀疏矩阵
#include <iostream>
#include <iomanip> // 控制输入输出格式等
#include <cmath>using namespace std;
using namespace Eigen;const double DERIV_STEP = 1e-5;
const int MAX_INTER = 100;#define max(a, b) (((a)>(b))?(a):(b))// 定义目标函数
double func(const VectorXd input, const VectorXd &output, const VectorXd ¶ms, int objIndex)
{// obj = A * sin(Bx) + C * cos(D*x) - Fdouble x1 = params(0); // params 中存储的是系数double x2 = params(1);double x3 = params(2);double x4 = params(3);double t = input(objIndex); // input 中存储的是 xdouble f = output(objIndex); // output 中存储的是实际值return x1 * sin(x2 * t) + x3 * cos(x4 * t) - f; // 返回 objIndex 项的残差
}// 计算残差矩阵
VectorXd objF(const VectorXd &input, const VectorXd &output, const VectorXd ¶ms)
{VectorXd obj(input.rows()); // 存储所有残差,也就是残差矩阵for (int i = 0; i < input.rows(); i++)obj(i) = func(input, output, params, i);return obj; // 返回残差矩阵
}// 残差平方和
double Func(const VectorXd &obj)
{return obj.squaredNorm() / 2.0;
}// 求某个系数在某点的导数
double Deriv(const VectorXd &input, const VectorXd &output, int objIndex, const VectorXd ¶ms, int paraIndex)
{VectorXd para1 = params;VectorXd para2 = params;para1(paraIndex) -= DERIV_STEP;para2(paraIndex) += DERIV_STEP;double obj1 = func(input, output, para1, objIndex);double obj2 = func(input, output, para2, objIndex);return (obj2 - obj1) / (2 * DERIV_STEP); // 该点处的导数,为求雅克比矩阵做准备
}// 计算雅克比矩阵
/***************************** 我们优化的是系数 params,把他们看做未知数,分别求导,得到雅克比矩阵* 维度:(input.rows() x output.rows())* [[df/dA df/dB df/dC df/dD] <--- x1* [df/dA df/dB df/dC df/dD] <--- x2* [.......................]* [df/dA df/dB df/dC df/dD]] <--- xn****************************/
MatrixXd Jacobian(const VectorXd &input, const VectorXd &output, const VectorXd ¶ms)
{int rowNum = input.rows();int colNum = params.rows();MatrixXd Jac(rowNum, colNum);for (int i = 0; i < rowNum; i++)for (int j = 0; j < colNum; j++)Jac(i, j) = Deriv(input, output, i, params, j);return Jac;
}//求 Hessian 矩阵对角线最大值
// Hessian 矩阵:二阶导数
double maxMatrixDiagonale(const MatrixXd &Hessian)
{int max = 0;for (int i = 0; i < Hessian.rows(); i++){if(Hessian(i, i) > max)max = Hessian(i, i);}return max;
}double linerDeltaL(const VectorXd &step, const VectorXd &gradient, const double u)
{double L = step.transpose() * (u * step - gradient);return L;
}void levenMar(const VectorXd &input, const VectorXd &output, VectorXd ¶ms)
{int errNum = input.rows();int paraNum = params.rows();// initial parametersVectorXd obj = objF(input, output, params); // 得到误差矩阵MatrixXd Jac = Jacobian(input, output, params); // 得到雅克比矩阵MatrixXd H = Jac.transpose() * Jac; // 得到 Hessian 矩阵,4x4VectorXd gradient = Jac.transpose() * obj; // 也就是 g,4x1double tao = 1e-3;long long v = 2;double epsilon1 = 1e-12, epsilon2 = 1e-12;double u = tao * maxMatrixDiagonale(H); // Hessian 矩阵对角线最大值乘 taobool found = gradient.norm() <= epsilon1;if (found) return; // 直接退出程序,不再执行后面的程序double last_sum = 0;int iterCnt = 0; // 迭代计数while (iterCnt < MAX_INTER){VectorXd obj = objF(input, output, params); // 误差矩阵MatrixXd Jac = Jacobian(input, output, params); // 得到雅克比矩阵MatrixXd H = Jac.transpose() * Jac; // 得到 Hessian 矩阵,4x4VectorXd gradient = Jac.transpose() * obj; // 也就是 g,4x1if(gradient.norm() < epsilon1){cout << "stop g(x) = 0 for a local minimizer optimizer." << endl;break;}cout << "H:" << endl << H << endl;VectorXd step = (H + u * MatrixXd::Identity(paraNum, paraNum)).inverse() * gradient;// 求 Delta x = (H + uI)^{-1}g 注意:step 维度(4x1)cout << "step: " << endl << step << endl;if(step.norm() <= epsilon2 * (params.norm()) + epsilon2){cout << "stop because change in x is small" << endl;break;}VectorXd paramsNew(params.rows());paramsNew = params - step; // 更新 params// 计算 params 误差obj = objF(input, output, params);// 计算 paramsNew 误差VectorXd obj_new = objF(input, output, paramsNew);double deltaF = Func(obj) - Func(obj_new); // 求差double deltaL = linerDeltaL(-1 * step, gradient, u);// 计算增益系数 rhodouble rho = deltaF / deltaL; // 实际下降值 / 近似下降值cout << "rho is; " << rho <<endl;if(rho > 0){params = paramsNew;u *= max(1.0 / 3.0, 1 - pow(2 * rho - 1, 3));v = 2;} else{u = u * v;v = v * 2;}cout << "u= " << u << "\tv= " << v << endl;iterCnt ++;cout << "Iteration " << iterCnt << " times, result is :" << endl<< params << endl;}
}int main()
{int params_num = 4;int total_data = 100;VectorXd input(total_data);VectorXd output(total_data);double A = 5, B = 1, C = 10, D = 2; // 初始化// 生成数据for (int i = 0; i < total_data; i++){double x = 20.0 * ((rand() % 1000) / 1000.0) - 10.0; // [-10, 10]double deltaY = 2.0 * (rand() % 1000) / 1000.0; // 随机噪声,[0, 2]double y = A * sin(B*x) + C * cos(D*x) + deltaY;input(i) = x;output(i) = y;}VectorXd params_levenMar(params_num);params_levenMar << 3.6, 1.3, 7.2, 1.7;levenMar(input, output, params_levenMar);cout << "Levenberg-Marquardt parameter: " << endl << params_levenMar << endl << endl << endl;cout << "**********************************************" << endl;}相关文章:

01 LM 算法及 Cpp 实现
文章目录 01 LM 算法及 Cpp 实现1.1 应用1.2 阻尼法推导1.3 Cpp 算法实现 01 LM 算法及 Cpp 实现 1.1 应用 LM 算法用于解决非线性最小二乘问题 min x F ( x ) 1 2 ∥ f ( x ) ∥ 2 2 (1) \min _x F(x)\frac{1}{2}\|f(\boldsymbol{x})\|_2^2 \tag{1} xminF(x)21∥f(x…...

【网络安全架构】互联网正对中国社会、经济、文化等各个领域产生巨大影响‘
摘 要: 中国互联网近年来飞速发展,普及率达到38.4%。已稳居世界第一网民大国的地位。互联网正对社会、经济、文化等各个领域产生巨大影响。2011年12月21日“泄密门”事件,再次敲响网络安全的警钟。网络攻击和入侵都是根据网络模型不同层次的特…...

【笔记】Android ServiceStateTracker 网络状态变化逻辑及SPN更新影响
业务简介 在网络状态变化的时候(数据或WiFi),会更新SPN。 基于Android U的代码分析。 分类:SPN Data_Dic-的博客-CSDN博客 功能逻辑 状态说明 飞行模式下注册上WFC的话,注册状态MD上报 regState: NOT_REG_MT_NOT…...

2PC和3PC的区别是什么
2PC提交协议是什么 二阶段提交是指,在计算机网络一级数据库领域内,为了使基于分布式系统的架构下的所有节点在进行事务提交时保持一致性而设计的一种算法。在分布式系统中,每个节点虽然可以知晓自己操作的成功和失败,但是无法知道…...
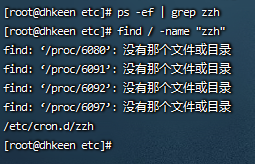
redis未设置密码被植入挖矿脚本
最近一台测试linux响应速度贼慢,检查发现cpu消耗高达100%!查看进程杀死后过段时间又重启了,一时间也摸不到头绪。无意间发现启动redis的时候cpu瞬间拉到了100%,主要就是zzh和newinit.sh两个脚本。百度了一下说是被植入了挖矿脚本&…...

轮询--一起学习吧之架构
一、定义 轮询(Polling)是一种CPU决策如何提供周边设备服务的方式,又称“程控输出入”(Programmed I/O)。这种方式是由CPU定时发出询问,依序询问每一个周边设备是否需要其服务,有即给予服务&am…...
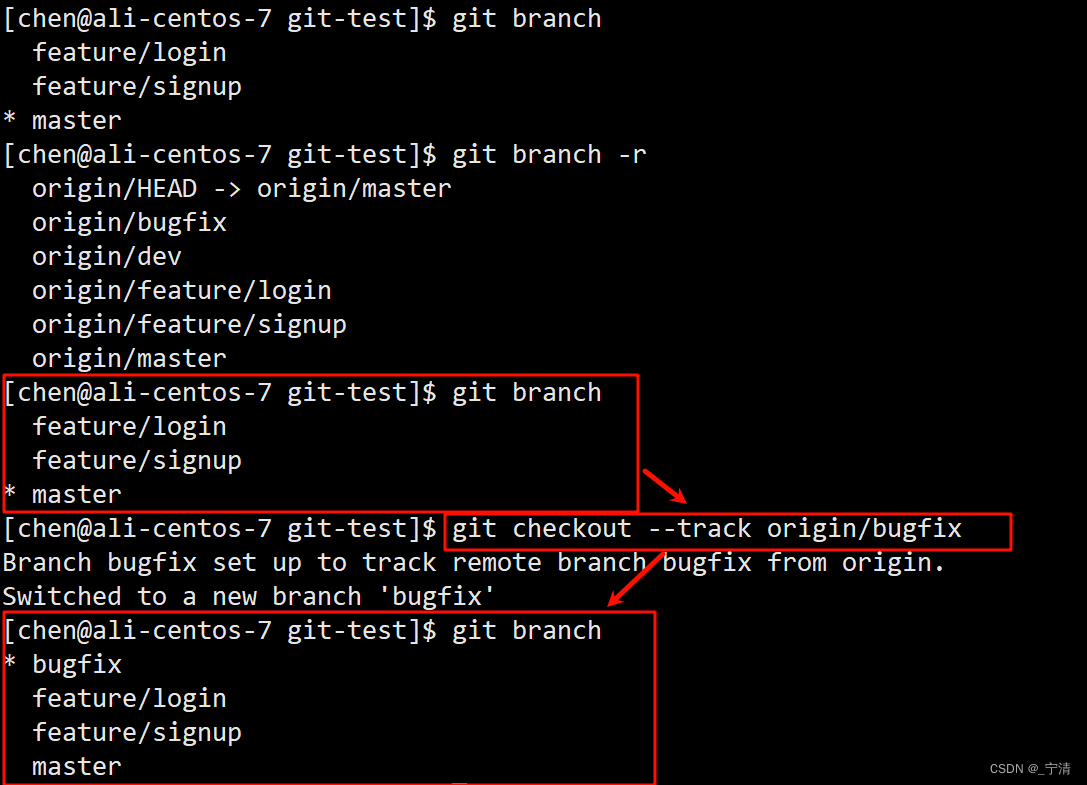
【开发工具】Git模拟多人开发场景理解分支管理和远程仓库操作
我们来模拟一个多人多分支的开发场景。假设你有一个新的空白远程仓库,假设地址是 https://github.com/user/repo.git。 克隆远程仓库到本地 $ git clone https://github.com/user/repo.git这会在本地创建一个 repo 目录,并自动设置远程主机为 origin。 创建本地开发分支并推送…...

从零学习Linux操作系统 第三十一部分 ansible常用模块介绍
一、ansible运行模块的两种方式 Ad-Hoc方式 ##利用ansible命令直接完成管理,主要用于临时命令使用场景 playbook方式 ##ansible脚本,主要用于大型项目场景,需要前期的规划,相当于shell当中的脚本 二、如何查看模块帮助 ansible…...

【Linux C | 网络编程】多播的概念、多播地址、UDP实现广播的C语言例子
😁博客主页😁:🚀https://blog.csdn.net/wkd_007🚀 🤑博客内容🤑:🍭嵌入式开发、Linux、C语言、C、数据结构、音视频🍭 🤣本文内容🤣&a…...

HarmonyOS NEXT应用开发案例——滑动页面信息隐藏与组件位移效果
介绍 在很多应用中,向上滑动"我的"页面,页面顶部会有如下变化效果:一部分信息逐渐隐藏,另一部分信息逐渐显示,同时一些组件会进行缩放或者位置移动。向下滑动时则相反。 效果图预览 使用说明 向上滑动页面…...

ffmpeg 转码过程中参数含义
ffmpeg 转码过程中参数含义 frame 649 fps 73 q28.0 size 3072kB time00:00:25.88 bitrate 972.4kbits/ frame 694 fps 74 q28.0 size 3328kB time00:00:27.68 bitrate 984.9kbits/ frame 732 fps 74 q28.0 size 3584kB time00:00:29.20 bitrate1005.5kbits/ fram…...
探索c++——了解c++的魅力
前言:c是一门既面向对象又面向过程的语言。 不同于java纯粹的面向对象和c纯粹的面向过程。 造成c该特性的原因是c是由本贾尼大佬在c的基础上增添语法创建出来的一门新的语言。 它既兼容了c, 身具面向过程的特性。 又有本身的面向对象的特性。 面向对象和…...

Oracle常用语句语法
1 第一章Oracle命令 转载至 Oracle常用语句语法汇总 https://www.modb.pro/db/1759752946170548224 a) 系统管理员连接 conn */* as sysdba b) 查询当前用户 show user c) 创建新用户 create user 用户名 identified by 密码(密码不能以数字开头)。例如…...

时隔n年再度会看Vue,Git
时隔n年再度会看Vue,Git 曾经沧海难为水,除却巫山不是云。不知道这句话用在这里合不合适,好多东西在记忆中都淡化了。但是互联网确是有记忆的。研究以前项目的时候,翻看到gitee码云上托管的项目,就像是自己的孩子重新又回来了一样…...

SpringCloud-Zuul网关的使用
在SpringCloud中网关Zuul起什么作用? 在Spring Cloud中,Zuul 是一个边缘服务网关,起着以下作用:反向代理:Zuul 可以作为应用程序的反向代理服务器,接收客户端请求并将请求转发给相应的服务。这使得客户端可…...

mysql 中的一些重要函数
show create table user_profile 查看表结构 1.datediff(end_date,start_date)函数,now(), curdate() curtime() date_add(日期,interval num 时间) date_format(日期,格式) 4.select IFNULL(null,0); oracle 中nvl 函数 5.select IF(2 > 1, 2,0)ÿ…...
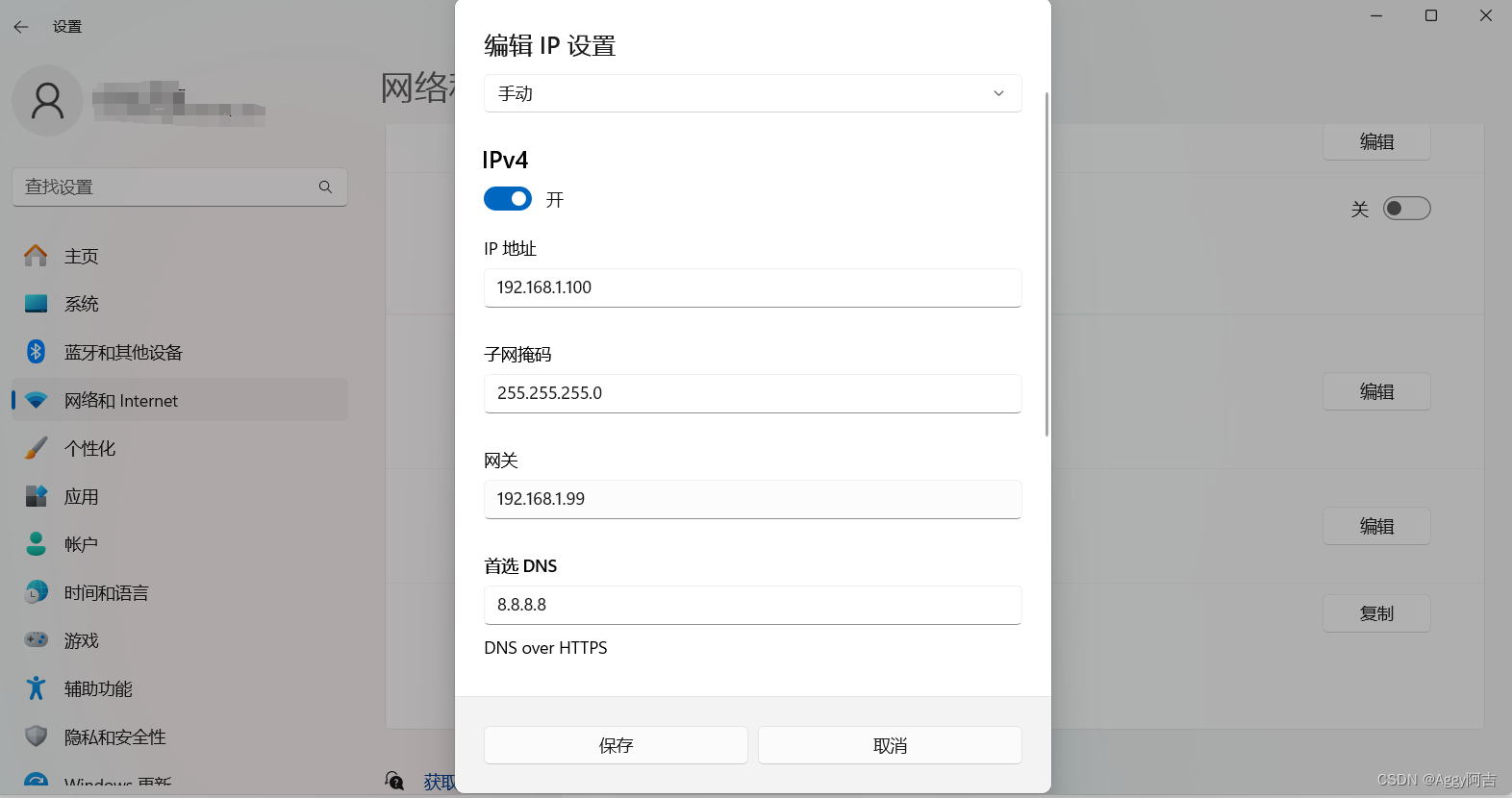
windows11配置电脑IP
windows11配置电脑IP 选择"开始>设置>“网络&Internet >以太网”。在 "属性"下,编辑IP地址,子网掩码,网关以及DNS。...

【JavaEE】_前端POST请求使用json向后端传参
目录 1. 关于json 2. 通过Maven仓库,将Jackson下载导入到项目中 3. 使用Jackson 3.1 关于readValue方法 3.2 关于Request.class类对象 3.3 关于request对象的属性类型 3.4 关于writeValueAsString 前端向后端传递参数通常有三种方法: 第一种&…...

大语言模型系列-GPT-2
文章目录 前言一、GPT-2做的改进二、GPT-2的表现总结 前言 《Language Models are Unsupervised Multitask Learners,2019》 前文提到,GPT-1利用不同的模型结构微调初步解决了多任务学习的问题,但是仍然是预训练微调的形式,GPT-…...
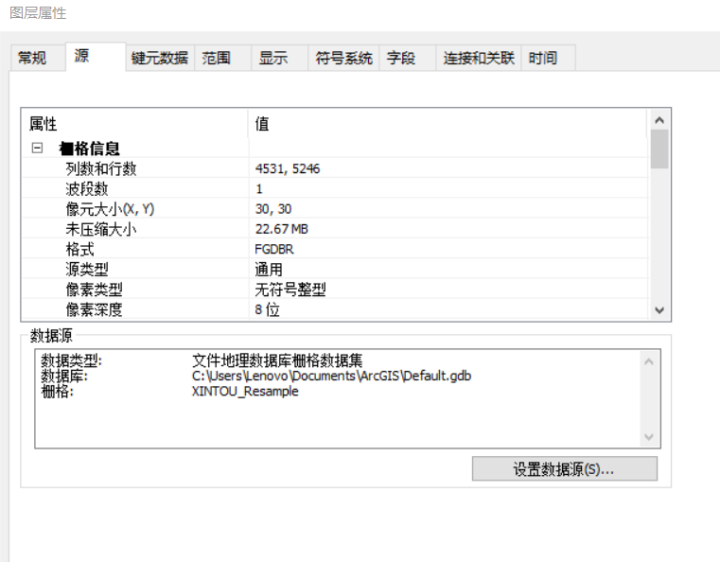
30m二级分类土地利用数据Arcgis预处理及获取
本篇以武汉市为例,主要介绍将土地利用数据转换成武汉市内各区土地利用详情的过程以及分区统计每个区内各地类面积情况,后面还有制作过程中遇到的面积制表后数据过小的解决方法以及一些相关的知识点: 示例数据下载链接:数据下载链…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...
