C语言题目练习
目录
前言
1、转置矩阵
1.1 题目
描述
输入描述:
输出描述:
1.2解题
分析:
程序:
2、KiKi判断上三角矩阵
2.1 题目
描述
输入描述:
输出描述:
2.2 解题
分析:
程序:
3、有序序列判断
3.1 题目
描述
输入描述:
输出描述:
3.2解题
分析:
程序:
结语
前言
纸上得来终觉浅,觉知此事要躬行。C语言的学习不仅要了解理论知识,更要不断练习,在练习中成长。下面我将给出几到例题,并分析讲解,帮助我们在实践中了解C语言。
1、转置矩阵
1.1 题目
描述
KiKi有一个矩阵,他想知道转置后的矩阵(将矩阵的行列互换得到的新矩阵称为转置矩阵),请编程帮他解答。
输入描述:
第一行包含两个整数n和m,表示一个矩阵包含n行m列,用空格分隔。 (1≤n≤10,1≤m≤10)
从2到n+1行,每行输入m个整数(范围-231~231-1),用空格分隔,共输入n*m个数,表示第一个矩阵中的元素。
输出描述:
输出m行n列,为矩阵转置后的结果。每个数后面有一个空格。

1.2解题
分析:
此题就是一个对二维数组的操作,只需要在输入时按照行和列的顺序输入,输出时按照列到行反过来输出即可。
程序:
int main()
{int a[10][10] = { 0 };int n = 0;int m = 0;scanf("%d%d", &n, &m);for (int i = 0;i < n;i++){for (int j = 0;j < m;j++){scanf("%d", &a[i][j]);}}for (int i = 0;i < m;i++){for (int j = 0;j < n;j++){printf("%d ", a[j][i]);}printf("\n");}return 0;
}2、KiKi判断上三角矩阵
2.1 题目
描述
KiKi想知道一个n阶方矩是否为上三角矩阵,请帮他编程判定。上三角矩阵即主对角线以下的元素都为0的矩阵,主对角线为从矩阵的左上角至右下角的连线。
输入描述:
第一行包含一个整数n,表示一个方阵包含n行n列,用空格分隔。 (2≤n≤10)
从2到n+1行,每行输入n个整数(范围-231~231-1),用空格分隔,共输入n*n个数。
输出描述:
一行,如果输入方阵是上三角矩阵输出"YES"并换行,否则输出"NO"并换行。

2.2 解题
分析:
此题先输入数据,然后对左下角的数据进行判断,只要出现非0则不为上三角矩阵,输出NO。如果判断完成后未发现问题,则为上三角矩阵,输出YES
程序:
#include <stdio.h>
int main()
{int n = 0;scanf("%d", &n);int arr[10][10] = { 0 };int i = 0;int j = 0;int p = 1; //标记,如果是上三角矩阵,则为1,否则为0.for (i = 0;i < n;i++) //输入{for (j = 0;j < n;j++){scanf("%d", &arr[i][j]);}}for (i = 0;i < n;i++) //判断{for (j = 0;j < n;j++){if (((i - j) > 0) && (arr[i][j] != 0)){p = 0;goto end;}}}
end:if (p == 1){printf("YES\n");}else{printf("NO\n");}return 0;
}3、有序序列判断
3.1 题目
描述
输入一个整数序列,判断是否是有序序列,有序,指序列中的整数从小到大排序或者从大到小排序(相同元素也视为有序)。
数据范围:3≤n≤50 序列中的值都满足 1≤val≤100
输入描述:
第一行输入一个整数N(3≤N≤50)。
第二行输入N个整数,用空格分隔N个整数。
输出描述:
输出为一行,如果序列有序输出sorted,否则输出unsorted。
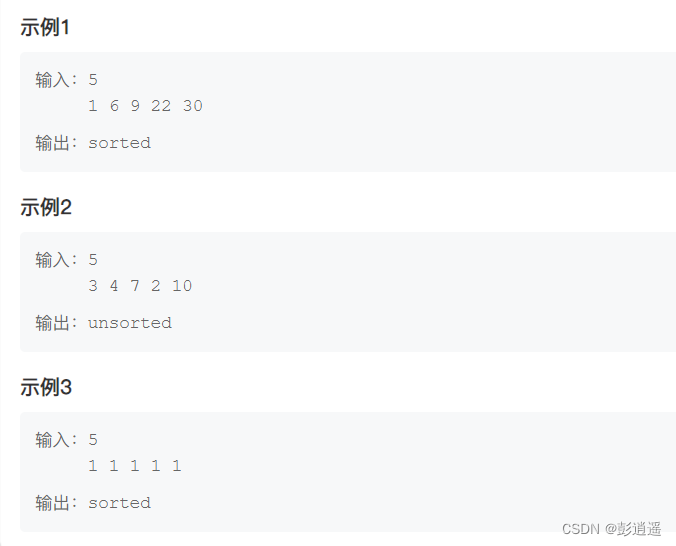
3.2解题
分析:
此题需要从两种情况进行分析:升序和降序。
用一个变量(我用的p)来标记升序和降序以及不升不降,然后看整个数列的升降情况是否统一,也就是在遍历整个数组时p是否改变。这里要注意的是,当前后两个数据相同时,并没有破坏数列的有序性,所以需要特别判断。
程序:
#include<stdio.h>
int main()
{int n = 0;scanf("%d", &n);int arr[50] = { 0 };int i = 0;int p = 0;int f = -1;int k = 1;for (i = 0;i < n;i++){scanf("%d", &arr[i]);}for (i = 1;i < n;i++){if (arr[i] > arr[i - 1]){p = 0; //降序标记}else if (arr[i] < arr[i - 1]){p = 1; //升序标记}else{p = -1; //未改变标记}if ((f != p) && (f != -1)){k = 0;}f = p;}if (k == 1){printf("sorted");}else{printf("unsorted");}return 0;
}结语
不要小瞧每一次练习,每天保持练习,持之以恒,我们的C语言技术才会越发熟练。希望大家都能越来越好,不辜负自己的努力。
相关文章:

C语言题目练习
目录 前言 1、转置矩阵 1.1 题目 描述 输入描述: 输出描述: 1.2解题 分析: 程序: 2、KiKi判断上三角矩阵 2.1 题目 描述 输入描述: 输出描述: 2.2 解题 分析: 程序: 3、…...

物联网安全|TrustAsia助力PSWG应对全球物联网产品安全合规挑战
万物互联时代,随着物联网连接数快速增长,物联网设备的潜在网络安全隐患也日益增长,可能导致设备故障、数据被盗、篡改、隐私泄露等问题的发生,甚至成为网络攻击的跳板,对互联网基础设施构成严重威胁。 我们看到&#…...
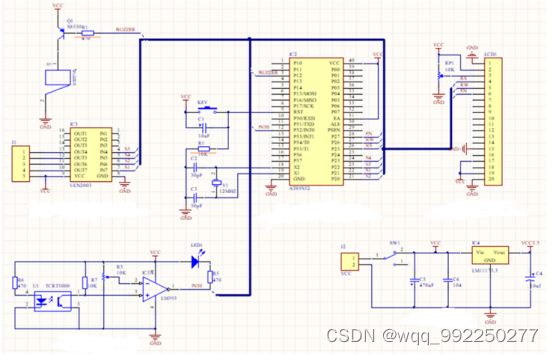
基于单片机的医院输液系统设计
目 录 摘 要 Ⅰ Abstract Ⅱ 引 言 1 1系统方案设计与论证 3 1.1系统硬件结构总体设计方案 3 1.2点滴速度测量电路方案的选择与论证 3 1.3液面检测电路方案的选择与论证 4 1.4通过电机控制滴速电路的方案与论证 4 1.5显示器接口电路方案选择与论证 5 1.6键盘接口电路方案选择与…...
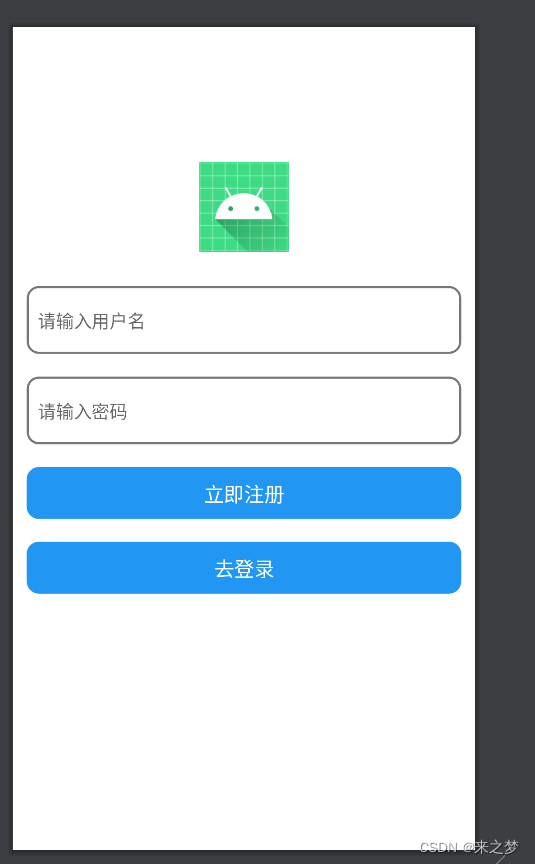
安卓简单登录
注意 有的朋友不知道登录咋写,这里我就简单给出相应代码,用的本地存储,没用网络请求,有需要可以替换成想要的,废话不多上代码 登录 import androidx.appcompat.app.AppCompatActivity;import android.content.Context…...

【计算机网络】DNS/ICMP协议/NAT技术
文章目录 一、DNS(Domain Name System)1.DNS背景2.域名3.浏览器中输入url后,发生的事情 二、ICMP协议1.什么是ICMP协议2.ICM功能3.ICMP的报文格式4.ping命令5.traceroute命令 三、NAT技术1.NAT技术背景2.NAT IP转换过程3.NAPT4.NAT技术的缺陷5.NAT和代理服务器 四、TCP/IP五层模…...

2403C++,C++20协程通道
原文 通道是一个可用来连接协程,实现不同协程间通信的并发安全队列. Test fun test know channel() runBlocking<Unit> {val channel Channel<Int>()//生产者val producer GlobalScope.launch {var i 0while (true) {delay(1000)channel.send(i)println("…...

C语言从入门到实战——预处理详解
预处理详解 前言一、预定义符号1.1 __FILE__1.2__LINE__1.3 __DATE__1.4__TIME__1.5__STDC__ 二、 #define定义常量三、 #define定义宏四、 带有副作用的宏参数五、 宏替换的规则六、宏函数的对比七、 #和##7.1 #运算符7.2 ##运算符 八、 命名约定九、 #undef十、命令行定义十一…...
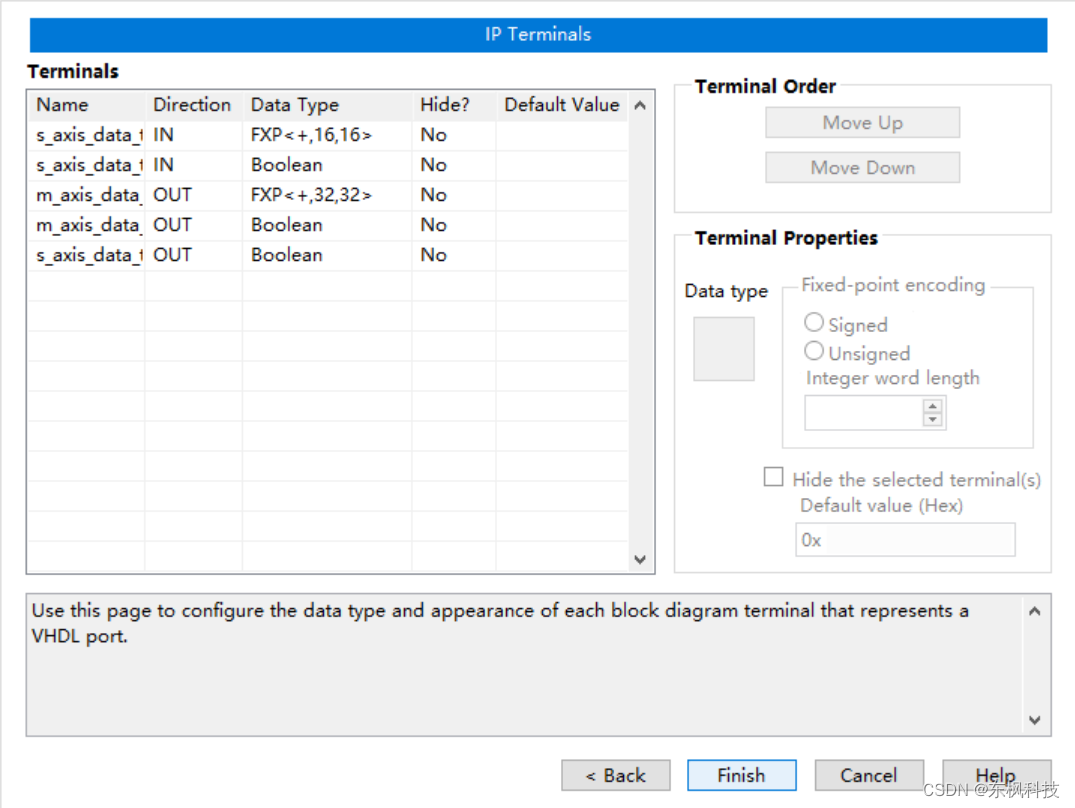
【LabVIEW FPGA】CIC滤波器
一、CIC滤波器应用概述 在通信数字信号上下变频时,经常会用到对数字信号的升采样和降采样,即通过CIC数字速率器实现变采样率。 二、滤波器IP 首先设置滤波器基本参数(filter specification) 滤波器类型(Filter Type…...

砝码称重 蓝桥杯
在C中,fabs()和abs()都用于计算数字的绝对值,但它们之间有一些区别。 fabs(double x):计算浮点数x的绝对值,返回一个double类型的结果。 abs(int x):计算整数x的绝对值,返回一个int类型的结果。 数组的默…...
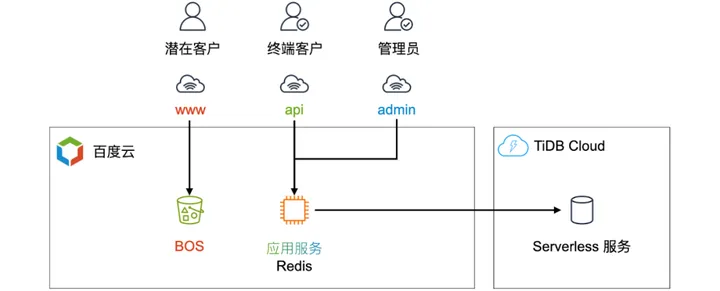
AmzTrends x TiDB Serverless:通过云原生改造实现全局成本降低 80%
本文介绍了厦门笛卡尔数据(AmzTrends)在面临数据存储挑战时,选择将其数据分析服务迁移到 TiDB Serverless 的思路和实践。通过全托管的数据库服务,AmzTrends 实现了全局成本降低 80% 的效果,同时也充分展示了 TiDB Ser…...
[最佳实践] Windows上构建一个和Linux类似的Terminal
感谢大佬批评指正,现已更新 preview Target:致力打造最赏心悦目Window下的终端,同时能够很接近Linux的使用习惯 key word:windows终端美化 windows terminal windows powershell 类似Linux下的Window终端 Window也能用ll windows…...
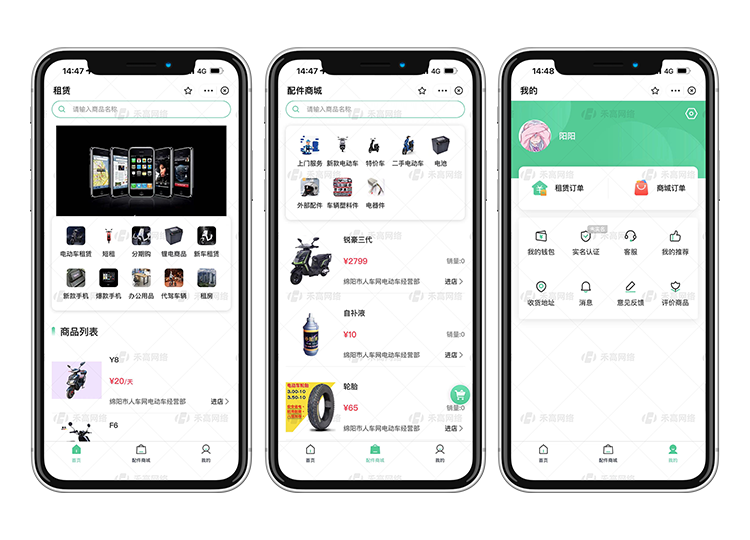
租赁系统|手机租赁软件|租赁系统功能开发
当如今的生活用品越来越多、交流更加便捷时,人们的消费需求也变得越来越丰富。不可避免地,我们会遇到这样一种情况:需要新的手机,但资金有限。此时,手机租赁小程序呼之欲出。这种创意不仅使我们能够充分利用各类闲置物…...
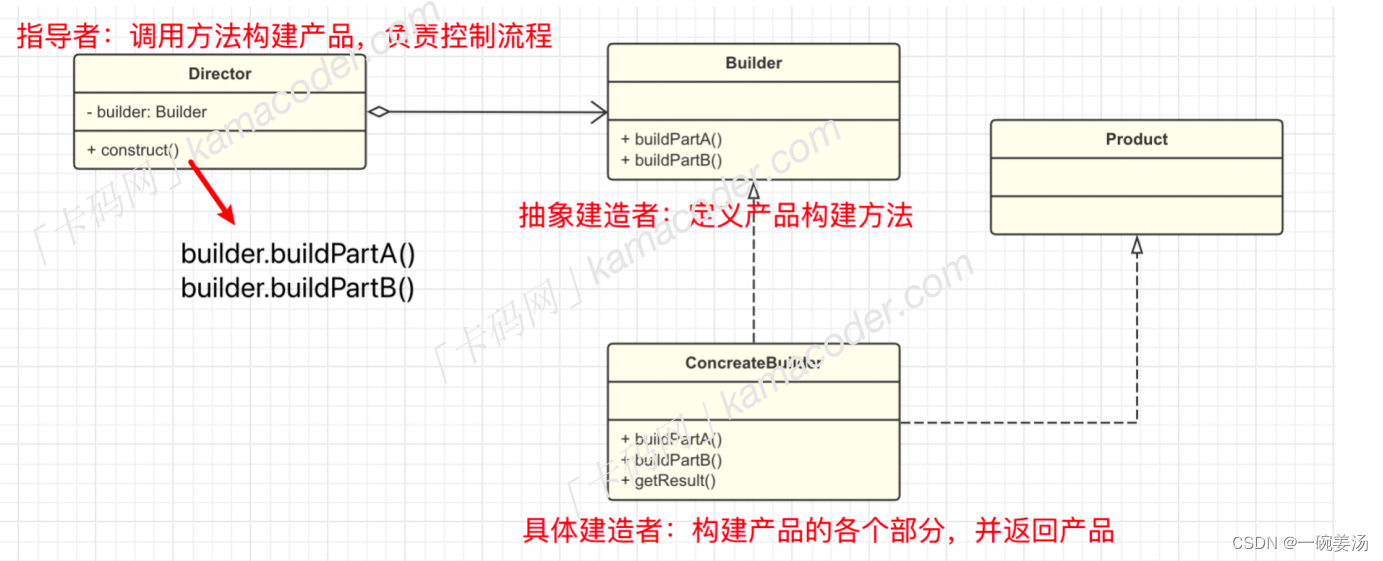
【设计模式 04】建造者模式
如果要构建的对象很复杂,那么可以将整个构建过程拆分成多个步骤,并为每一个步骤定义一个抽象的接口。并添加一个指导者用来控制构建产品的顺序和步骤。 Java实现: // 产品类 class Product {private String part1;private String part2;pub…...

Python使用错误总结
【1】cannot import name ‘ParameterSource’ from ‘click.core’ 其根本原因在于是black模块,其模块版本可能过时,升级black模块版本即可: pip install black --upgrade【2】partially initialized module ‘charset_normalizer’ has n…...
【Java EE初阶三十】JVM的简单学习
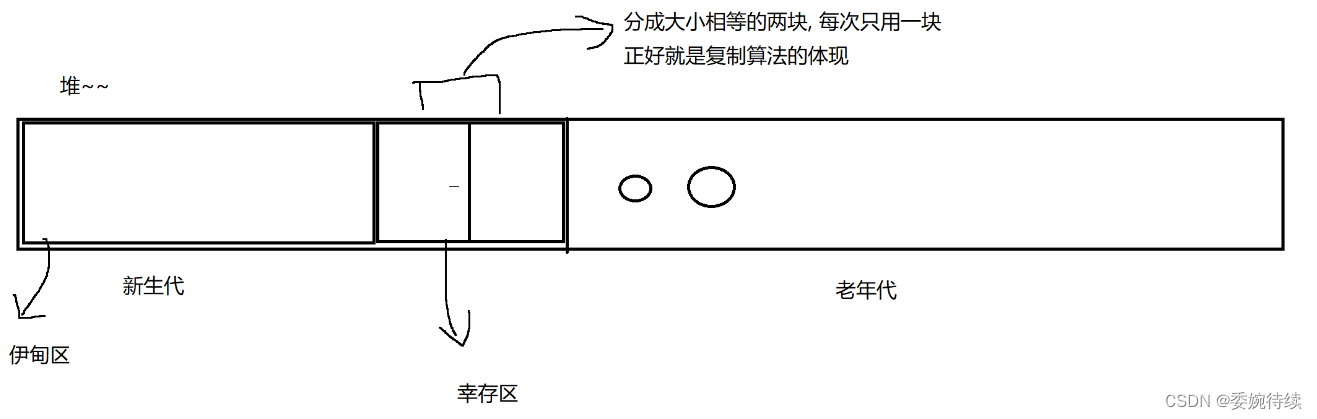
1. JVM 内存区域划分 一个运行起来的 Java 进程,就是一个 JVM 虚拟机,需要从操作系统申请一大块内存,就会把这个内存,划分成不同的区域,每个区域都有不同的作用. JVM 申请了一大块内存之后,也会划分成不同的内…...

thinkphp5水平分割表partition,以及查询操作
前言 先交代下背景,在一个项目中,有一个数据表有水平分表的需求。当时想找到一种方法,把对数据库的操作,写到一个模型里,通过去换模型属性中的table来达到代码不变操作的数据表变化的效果。 我们都知道,模型要想关联数据表的话&a…...
docker部署aria2-pro
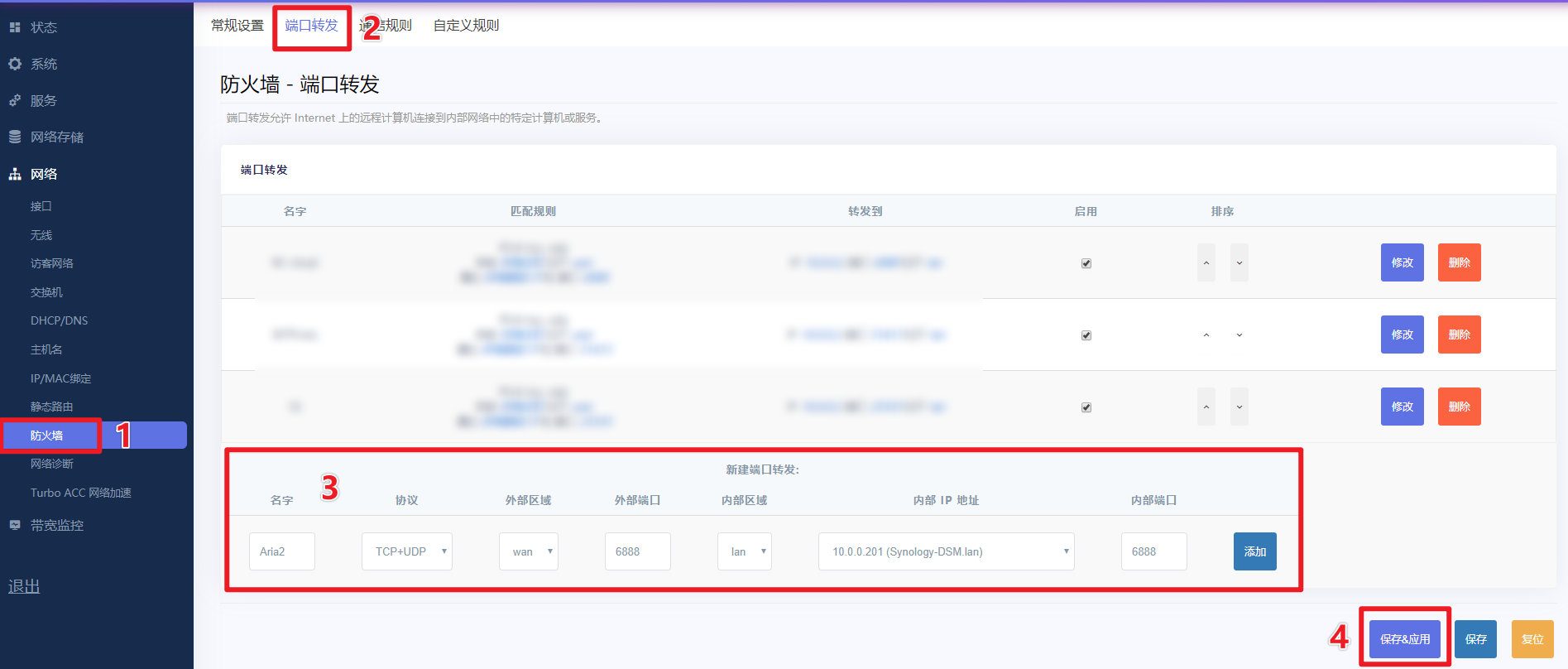
前言 我平时有一些下载视频和一些资源文件的需求,有时候需要离线下载,也要速度比较快的方式 之前我是用家里的玩客云绝育之后不再写盘当下载机用的,但是限制很多 我发现了aria2 这个下载器非常适合我,而有个大佬又在原来的基础…...
vue中Mixins
使用 Mixins 的主要优点包括: 代码复用: 可以将常用的逻辑封装在 Mixin 中,然后在多个组件中重复使用。逻辑分离: 将不同功能的代码分开管理,使代码更加清晰和易于维护。灵活性: Mixins 允许你在组件中引入多个 Mixin,并且可以根…...
)
linux常用指令(定期更新)
linux常用指令 1.页相关页大小 2.系统参数3.启动参数4.网络参数查询网卡所属numa节点信息网络测速相关iperf测试sar监控网卡流量查看网卡txqueuelen和mtu抓包tcpdump 网络数据收发状态snmp协议栈netstat -i所有网口TX-OK、RX-OKnetstat-s查看各个协议的收发数据ethtool -S单个网…...

【项目】图书管理系统
目录 前言: 项目要求: 知识储备: 代码实现: Main: Books包: Book: BookList: Operate包: Operate: addOperate: deleteOperate: exitOperate: findOperate:…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...

Pydantic + Function Calling的结合
1、Pydantic Pydantic 是一个 Python 库,用于数据验证和设置管理,通过 Python 类型注解强制执行数据类型。它广泛用于 API 开发(如 FastAPI)、配置管理和数据解析,核心功能包括: 数据验证:通过…...
