无人机|LQR控制算法及其无人机控制中的应用仿真
前言
LQR全称Linear Quadratic Regulator(线性二次调节器),顾名思义用于解决形如
x ˙ = A x + B u y = C x + D u \begin{aligned}\dot{x}&=Ax+Bu\\y&=Cx+Du\end{aligned} x˙y=Ax+Bu=Cx+Du
线性时不变系统的一种线性控制方法,是最优控制方法的一种。
LQR通过全状态反馈将不同状态加权求和得到最优控制量,本文所讨论的是无限时间LQR问题,即可以保证系统是渐进稳定的,不考虑收敛时间。该方法主要思想是构造以状态量以及控制量相关的二次代价函数,通过最小化该代价函数寻找成本最低的解。
LQR基本原理
考虑形如
x ˙ = A x + B u y = C x + D u \begin{aligned}\dot{x}&=Ax+Bu\\y&=Cx+Du\end{aligned} x˙y=Ax+Bu=Cx+Du的系统
其中控制量满足
u = − K x u=-Kx u=−Kx
K为反馈矩阵
考虑无穷时间内的代价函数,由于系统无稳态误差,故时间趋于无穷时终端约束项为0
构造代价函数为
m i n J = 1 2 ∫ 0 ∞ ( x T Q x + u T R u ) d t , Q = Q T , R = R T , Q ≥ 0 , R > 0 min J=\frac1{2}\int_0^\infty(x^TQx+u^TRu)dt,Q=Q^T,R=R^T,Q\geq0,R>0 minJ=21∫0∞(xTQx+uTRu)dt,Q=QT,R=RT,Q≥0,R>0
一般地,Q和R均为正定对角阵。
求解该代价函数最小时所对应的K矩阵,即可求得最优控制量。
matlab中可以直接使用工具包求解,如
K=lqr(A,B,Q,R)
公式推导
利用拉格朗日乘子法构造增广泛函
J , = ∫ 0 ∞ ( 1 2 ( x T Q x + u T R u ) + λ T ( A x + B u − x ˙ ) ) d t J^{,}=\int_0^\infty(\frac1{2}(x^TQx+u^TRu)+\lambda^T(Ax+Bu-\dot{x}))dt J,=∫0∞(21(xTQx+uTRu)+λT(Ax+Bu−x˙))dt
定义纯量函数,及哈密尔顿函数
H ( x , u , λ , t ) = 1 2 ( x T Q x + u T R u ) + λ T ( A x + B u ) H(x,u,\lambda,t)=\frac1{2}(x^TQx+u^TRu)+\lambda^T(Ax+Bu) H(x,u,λ,t)=21(xTQx+uTRu)+λT(Ax+Bu)
则有
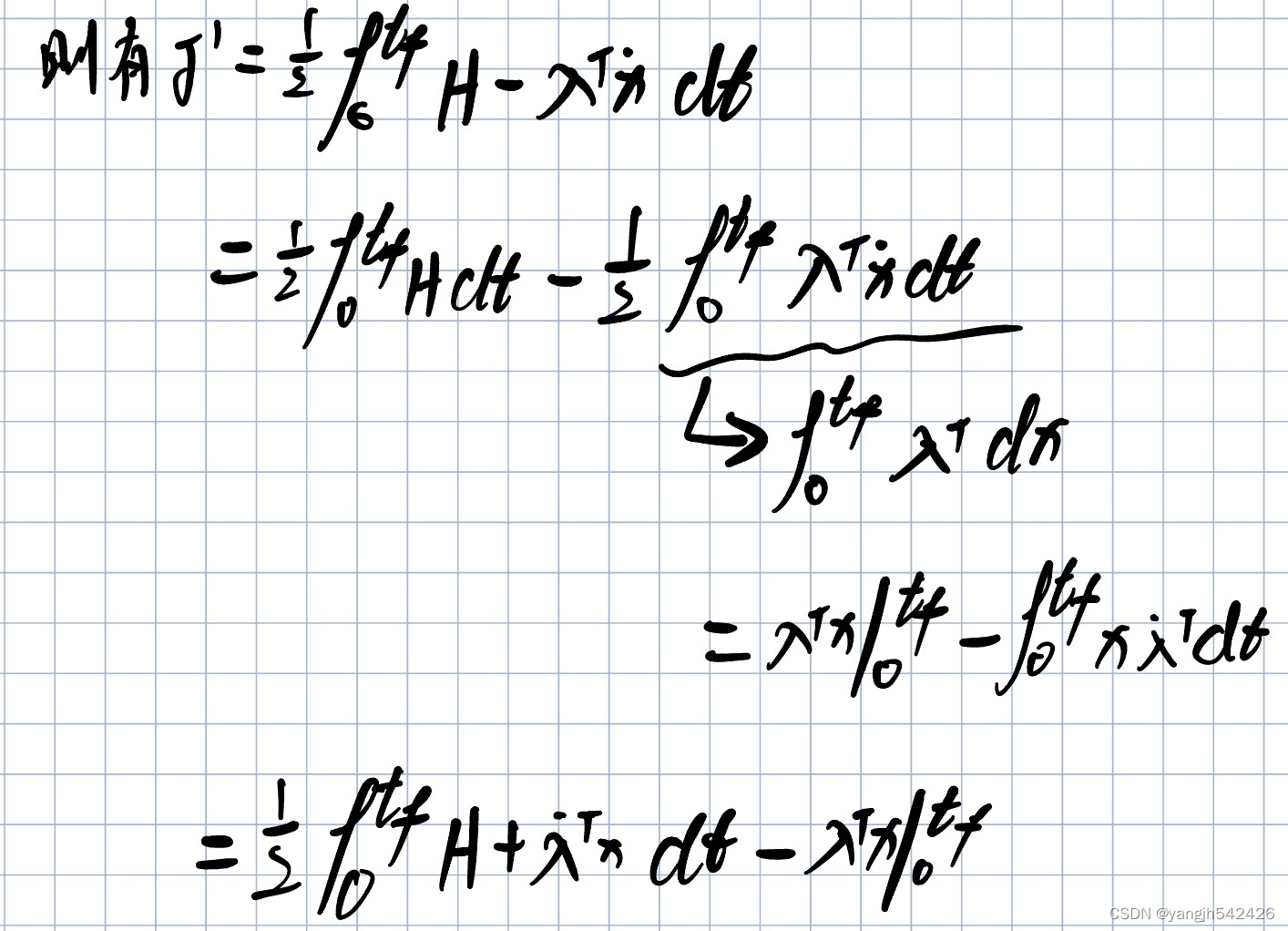
由变分法可得取极值时应满足控制方程
∂ H ∂ u = 0 \frac{\partial H}{\partial u}=0 ∂u∂H=0
则有
∂ H ∂ u = R u + B T λ = 0 \frac{\partial H}{\partial u}=Ru+B^T\lambda=0 ∂u∂H=Ru+BTλ=0
得
u ∗ = − R − 1 B T λ u^*=-R^{-1}B^T\lambda u∗=−R−1BTλ
又u应为关于x得线性表达,且由上式可得此时u为 λ \lambda λ的线性表达,故 λ \lambda λ也应为x的线性表达。
设
λ = P x \lambda=Px λ=Px
则有
u ∗ = − R − 1 B T P x u^*=-R^{-1}B^TPx u∗=−R−1BTPx
又根据正则方程
∂ H ∂ x + λ ˙ = 0 \frac{\partial H}{\partial x}+\dot\lambda=0 ∂x∂H+λ˙=0
∂ H ∂ λ = x ˙ \frac{\partial H}{\partial \lambda}=\dot x ∂λ∂H=x˙
得
λ ˙ = − ∂ H ∂ x = − Q x − A T λ = − Q x − A T P x \dot\lambda = -\frac{\partial H}{\partial x} = -Qx-A^T\lambda=-Qx-A^TPx λ˙=−∂x∂H=−Qx−ATλ=−Qx−ATPx
x ˙ = ∂ H ∂ λ = A x − B R − 1 B T P x \dot x=\frac{\partial H}{\partial \lambda}=Ax-BR^{-1}B^TPx x˙=∂λ∂H=Ax−BR−1BTPx
又对 λ = P x \lambda=Px λ=Px两边求导,得
λ ˙ = P ˙ x + P x ˙ \dot\lambda=\dot Px+P\dot x λ˙=P˙x+Px˙
P为常数矩阵时,则有
− Q x − A T P x = P A x − P B R − 1 B T P x -Qx-A^TPx = PAx-PBR^{-1}B^TPx −Qx−ATPx=PAx−PBR−1BTPx
又x为非零矩阵,则有
P A + A T P − P B R − 1 B T P + Q = 0 PA+A^TP-PBR^{-1}B^TP+Q=0 PA+ATP−PBR−1BTP+Q=0
即为riccati方程
求解该方程可得P
由此可解得 u ∗ = − R − 1 B T P x u^*=-R^{-1}B^TPx u∗=−R−1BTPx
仿真
在上篇基础上进行控制器修改
TODO
相关文章:
无人机|LQR控制算法及其无人机控制中的应用仿真
前言 LQR全称Linear Quadratic Regulator(线性二次调节器),顾名思义用于解决形如 x ˙ A x B u y C x D u \begin{aligned}\dot{x}&AxBu\\y&CxDu\end{aligned} x˙yAxBuCxDu 线性时不变系统的一种线性控制方法,…...
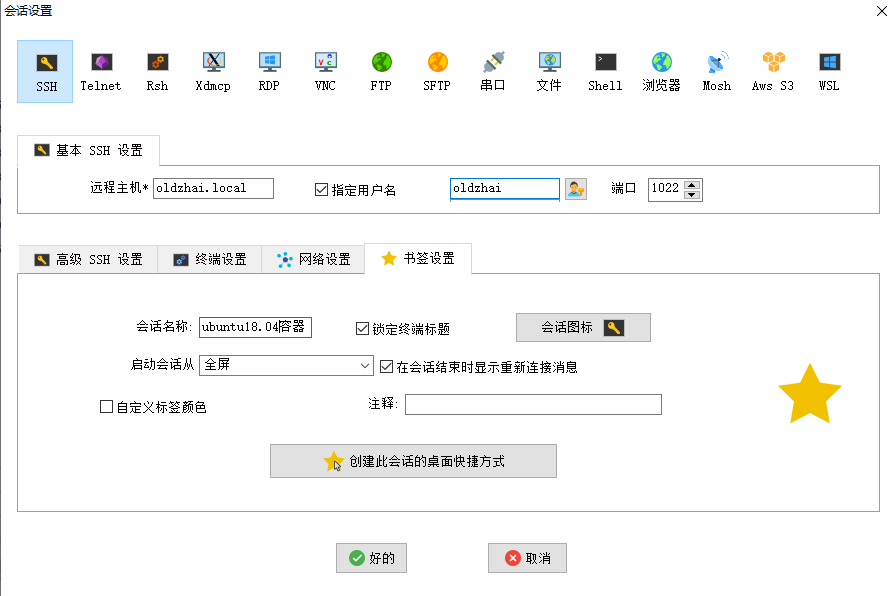
ubuntu环境下docker容器详细安装使用
文章目录 一、简介二、ubuntu安装docker1.删除旧版本2.安装方法一3. 安装方法二(推荐使用)4.运行Docker容器5. 配置docker加速器 三、Docker镜像操作1. 拉取镜像2. 查看本地镜像3. 删除镜像4. 镜像打标签5. Dockerfile生成镜像 四、Docker容器操作1. 获取…...

vue2源码分析-vue入口文件global-api分析
文章背景 vue项目开发过程中,首先会有一个初始化的流程,以及我们会使用到很多全局的api,如 this.$set this.$delete this.$nextTick,以及初始化方法extend,initUse, initMixin , initExtend, initAssetRegisters 等等那它们是怎么实现,让我们一起来探究下吧 源码目录 global-…...

Javascript原型 ,原型链如何理解使用 ?有什么特点?
文章目录 图解原型原型链总结有需要的请私信博主,还请麻烦给个关注,博主不定期更新,或许能够有所帮助!!请关注公众号 图解 原型 常被描述为 — 种基于原型的语言–每个对象拥有一个原型对象 当试图访问 一个对象的属性…...
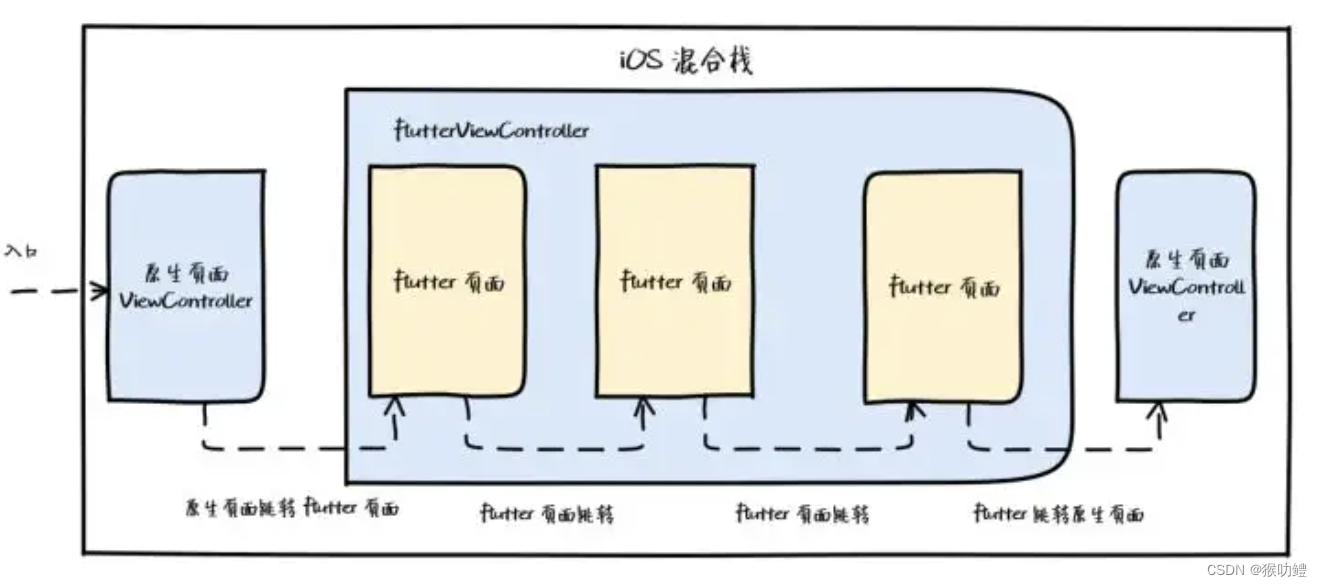
Flutter混合栈管理方案对比
1.Google官方(多引擎方案) Google官方建议的方式是多引擎方案,即每次使用一个新的FlutterEngine来渲染Widget树,存在的主要问题是每个引擎都要有比较大的内存等资源消耗,虽然Flutter 2.0之后的FlutterEngineGroup通过在…...

Asp .Net Core 集成 Newtonsoft.Json
简介 Newtonsoft.Json是一个在.NET环境下开源的JSON格式序列化和反序列化的类库。它可以将.NET对象转换为JSON格式的字符串,也可以将JSON格式的字符串转换为.NET对象。这个类库在.NET开发中被广泛使用,因为它功能强大、易于使用,并且有良好的性能。 使用Newtonsoft.Json,…...

GPT对话知识库——ARM-Cortex架构分为哪几个系列?每个系列有几种工作模式?各种工作模式之间的定义和区别?每种架构不同的特点和应用需求?
目录 1,问: 1,答: 2,问: 2,答: Cortex-A系列 Cortex-R系列 Cortex-M系列 3,问: 3,答: ARM Cortex-A架构 ARM Cortex-R架构…...
)
795. 前缀和(acwing)
文章目录 795.前缀和题目描述前缀和 795.前缀和 题目描述 输入一个长度为n的整数序列。 接下来再输入m个询问,每个询问输入一对l, r。 对于每个询问,输出原序列中从第l个数到第r个数的和。 输入格式 第一行包含两个整数n和m。 第二行包含n个整数&a…...
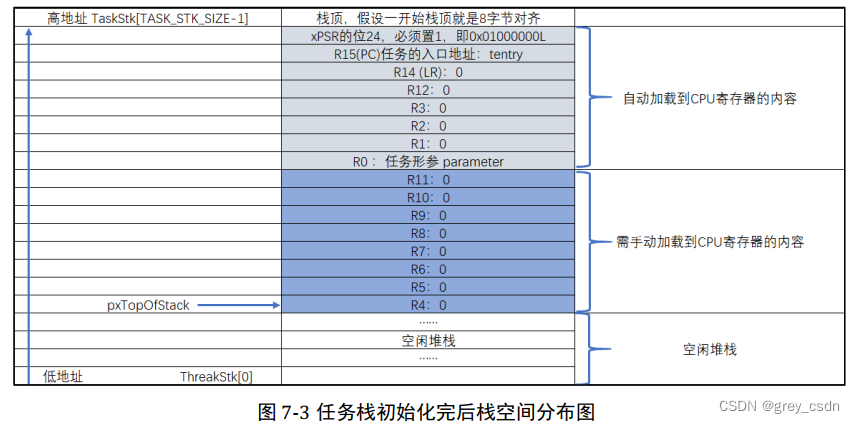
1910_野火FreeRTOS教程阅读笔记_prvStartFirstTask函数
1910_野火FreeRTOS教程阅读笔记_prvStartFirstTask函数 全部学习汇总: g_FreeRTOS: FreeRTOS学习笔记 这是教程中的一个函数,通过汇编来实现的。注释部分以及结合后面的讲解部分,可能还是有一点点细节的地方让初学者疑惑。我结合我自己的理解…...
图论练习5
Going Home Here 解题思路 模板 二分图最优匹配,前提是有完美匹配(即存在一一配对)左右集合分别有顶标,当时,为有效边,即选中初始对于左集合每个点,选择其连边中最优的,然后对于每…...

[C++] Volatile 和常量Const优化
Volatile的作用 volatile 表明某个变量的值可能在外部被改变,因此对这些变量的存取不能缓存到寄存器,每次使用时需要重新存取。 Const 和 Volatile的示例 示例1 int main() {const int a 1;int* pa const_cast<int*>(&a);*pa 4;cout &l…...

嵌入式学习day32 网络
htons();//host to network short 将端口号转换为网络通信中的大端存储 eg:htons(50000); ntohs();//host to network short 将大端存储转换为主机端口号 inet_addr();将IP地址转换为二进制 eg:inet_addr(192.168.1.170); inet_ntoa()…...

算法D33 | 贪心算法3 | 1005.K次取反后最大化的数组和 134. 加油站 135. 分发糖果
1005.K次取反后最大化的数组和 本题简单一些,估计大家不用想着贪心 ,用自己直觉也会有思路。 代码随想录 Python: class Solution:def largestSumAfterKNegations(self, nums: List[int], k: int) -> int:nums.sort(keylambda x: abs(x), reverseT…...

html地铁跑酷
下面是一个简单的HTML代码来展示一个地铁跑酷游戏: <!DOCTYPE html> <html> <head><title>地铁跑酷</title><style>#player {position: absolute;top: 0;left: 0;width: 50px;height: 50px;background-color: red;}</style…...
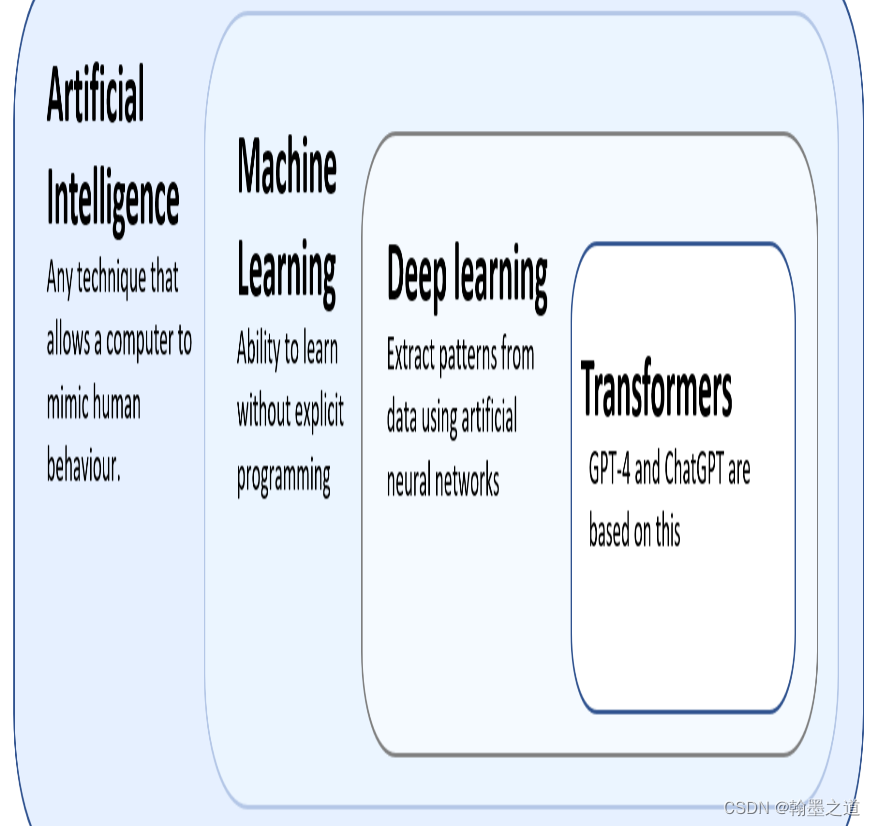
利用GPT开发应用001:GPT基础知识及LLM发展
文章目录 一、惊艳的GPT二、大语言模型LLMs三、自然语言处理NLP四、大语言模型LLM发展 一、惊艳的GPT 想象一下,您可以与计算机的交流速度与与朋友交流一样快。那会是什么样子?您可以创建哪些应用程序?这正是OpenAI正在助力构建的世界&#x…...

Golang Ants 构建协程池
构建的协程池实现两个目标: 1、限制协程池里开启的协程数量 2、当任务数大于协程数时,一个协程可以同时处理多个任务 3、监控是哪个协程ID处理了具体的任务 package mainimport ("fmt""runtime""strconv""string…...
)
【金三银四】面试题汇总(持续编写中)
Java八股文面试题汇总(持续编写中~) Java基础集合JUCJVM 数据库MySQLRedis 框架篇SSMSpringBoot 数据结构与算法数据结构与算法--汇总篇27道基础算法题,学完让你对算法有豁然开朗的感觉(推荐小白) 消息中间件RabbitMQK…...

Hive的数据存储
Hive的数据存储在HDFS的:/user/hive/warehouse中 The /user folder in HDFS is a directory typically used to store user-specific data and configurations. It serves as the home directory for Hadoop users, analogous to the /home directory in Unix-like …...
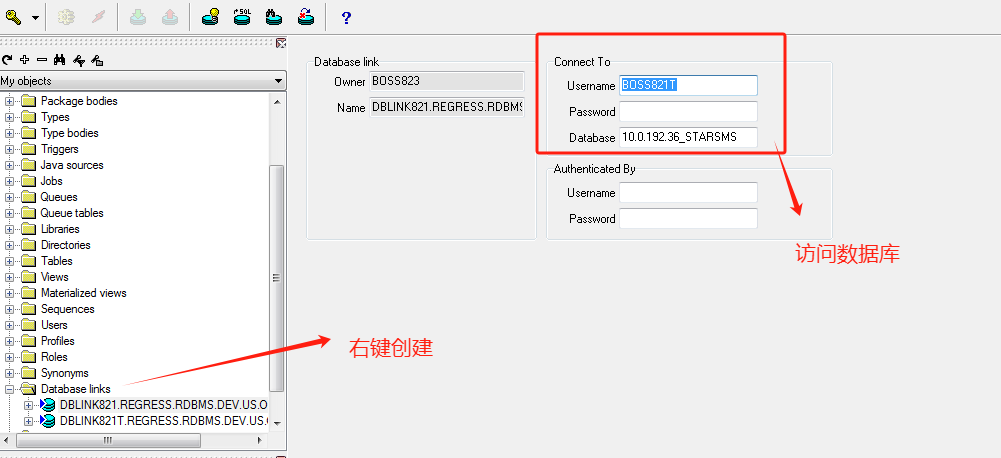
ORACLE 如何使用dblink实现跨库访问
dbLink是简称,全称是databaselink。database link是定义一个数据库到另一个数据库的路径的对象,database link允许你查询远程表及执行远程程序。在任何分布式环境里,database都是必要的。另外要注意的是database link是单向的连接。在创建dat…...
Sentinel 面试题及答案整理,最新面试题
Sentinel的流量控制规则有哪些,各自的作用是什么? Sentinel的流量控制规则主要包括以下几种: 1、QPS(每秒查询量)限流: 限制资源每秒的请求次数,适用于控制高频访问。 2、线程数限流…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...
