【数据结构与算法】常见排序算法(Sorting Algorithm)
文章目录
- 相关概念
- 1. 冒泡排序(Bubble Sort)
- 2. 直接插入排序(Insertion Sort)
- 3. 希尔排序(Shell Sort)
- 4. 直接选择排序(Selection Sort)
- 5. 堆排序(Heap Sort)
- 6. 快速排序(Quick Sort)
- 6.1 hoare快排(最早的快排方法)
- 优化快排(重要)
- 1. 减少函数递归的栈帧开销(虽然不用,但必须了解)
- 2.三位取中法取基准值(重点)
- 6.2 挖坑法快排
- 6.3 双指针法快排
- 6.4 非递归快排
- 快速排序的排序速度比较(包含测试代码)
- 7. 归并排序(Merge Sort)
- 7.1 递归版
- 7.2 非递归版
- 8. 计数排序
相关概念
- 排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
- 稳定性:说简单点就是有相同值时,排序后这些相同值互相顺序没发生变化则称为稳定的排序算法。假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
- 内部排序:数据元素全部放在内存中的排序(重点)。
- 外部排序:数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序(了解)。
常见排序算法时间、空间、稳定性:
- 直接插入排序:O(n2),正常情况下最快的O(n2)排序算法,稳定。
- 希尔排序:O(n1.3),比O(n*log2n)慢一点点,不稳定。
- 直接选择排序:O(n2),比冒泡快,比插入慢,不稳定。
- 堆排序:O(n*log2n),不稳定。
- 冒泡排序:O(n2),稳定。
- 快速排序: O(n*log2n),不稳定,空间O(log2n)。
- 归并排序 O(n*log2n),稳定,空间O(n)。
排序不特别说明,则排序以升序为例。
时间复杂度不特别说明,则默认最坏时间。
空间复杂度不特别说明,则默认O(1)。
1. 冒泡排序(Bubble Sort)
思想:两两比较,再交换。前一个值比后一个值大,交换两个值。


优化冒泡排序,冒泡排序优化版:

void BubbleSort(int* a, int n)
{int sortBorder = n - 1;int lastExchange = 0; for (int i = 0; i < n - 1; ++i) {bool isSorted = true; for (int j = 0; j < sortBorder; ++j) {if (a[j] > a[j + 1]) {Swap(&a[j], &a[j + 1]);isSorted = false;lastExchange = j;}}if (isSorted) {break;}sortBorder = lastExchange;}
}
void Swap(int* px, int* py)
{int tmp = *px;*px = *py;*py = tmp;
}
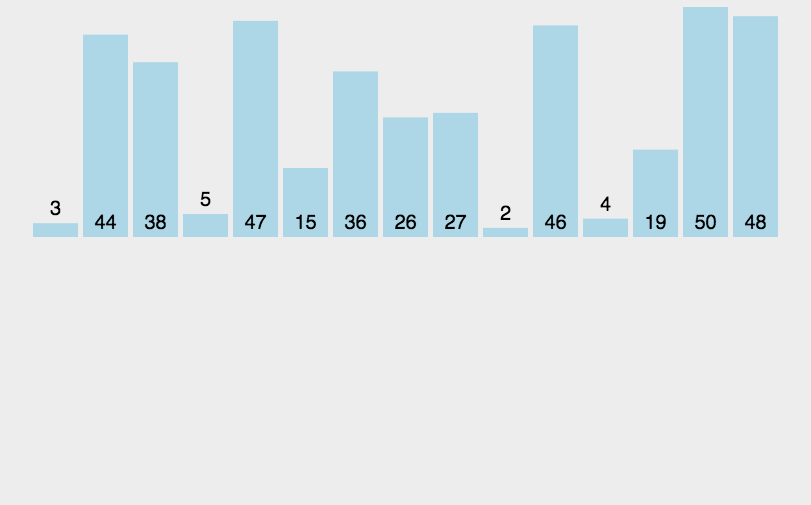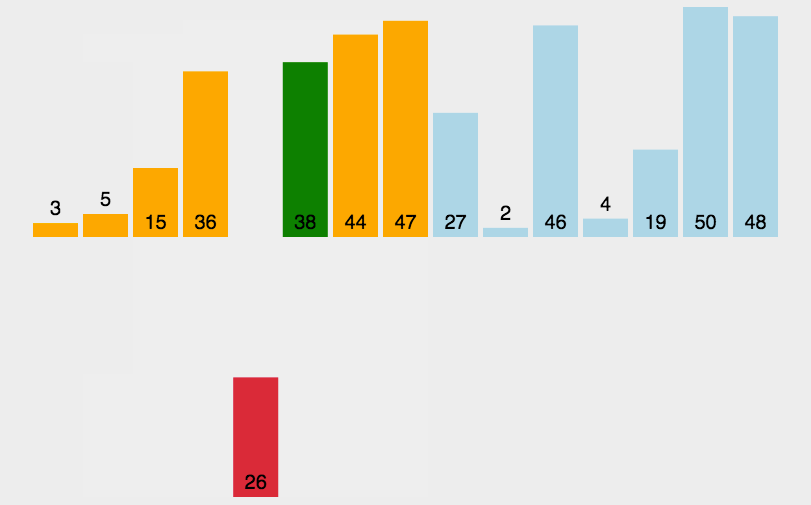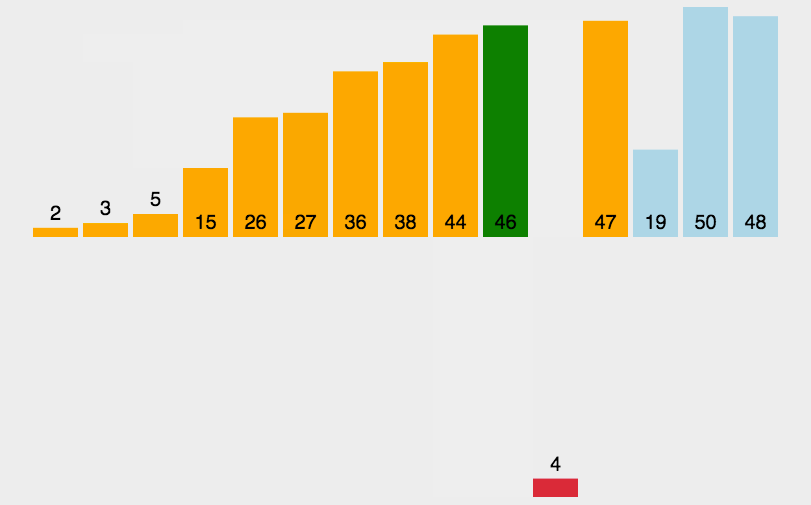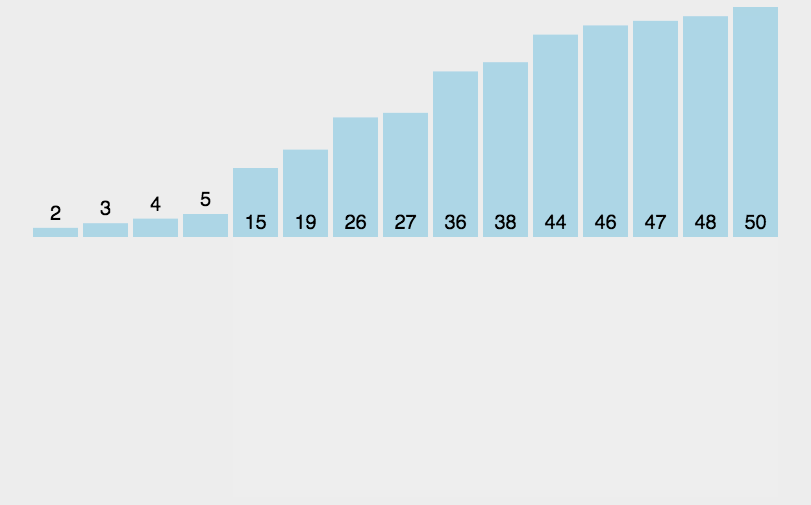
2. 直接插入排序(Insertion Sort)
思想:类似将扑克牌排序的过程,数据越有序,排序越快。

void InsertionSort(int* a, int n)
{for (int i = 0; i < n - 1; ++i){int end = i;int insertVal = a[end + 1];while (end >= 0 && insertVal < a[end]){a[end + 1] = a[end];--end;}a[end + 1] = insertVal;}
}
直接插入排序O(n*n),n方的排序中,直接插入排序是最有价值的。其它的如冒泡,直接选择排序等与直接插入排序一样N方的排序都是五十步和百步的区别,总体来看没啥区别,都不如直接插入排序,看以下几点分析以及排序时间比较,再就是大家自己编一串数据走查一下排序过程即可发现。
1.排升序而数据大致是降序,或排降序而数据大致是升序情况下,直接插入排序的时间复杂度是O(n*n),因为比较挪数据次数是等差数列之和。
2.数据大致有序,且排序顺序与数据顺序一致情况下,直接插入排序的时间复杂度是O(n),因为比较挪数据次数较少(不进入while循环)。比如排升序,而数据也大致也是升序状态(较为有序 或 直接就是有序的)。
3.虽然直接插入排序与冒泡排序的时间复杂度是同一个量级,但不谈上面第一种情况,
正常大多都是数据随机排列情况下前者比后者快很多,这时比较挪数据次数不会是等差数列之和,中间一般多少会有一部分是有序的,有那么几趟是不进入while循环的,比较挪数据次数当然是比等差数列之和要少的。虽然还是O(n*n)的量级,但明显是比冒泡快,至于快多少则是看有序的数据多不多(极限就是第二种情况)。
10w个数据 排序速度对比:

release环境是发布版本环境,对代码是有很大优化的,优化点大致是:
- 相比于debug环境,release环境生成的目标文件包含很少调试信息甚至没有调试信息。
- 减少了很多消耗性能或不必要的操作,不对代码进行边界检查,空指针检查、assert断言检查等。
- 特别是对递归优化巨大,也就是对函数栈帧的创建/栈的消耗优化很大,比如对于debug环境下栈溢出的程序,切换成release则不会造成栈溢出。
博主水平有限,不知道更多相关细节或是底层原理,如有错误恳请指正。
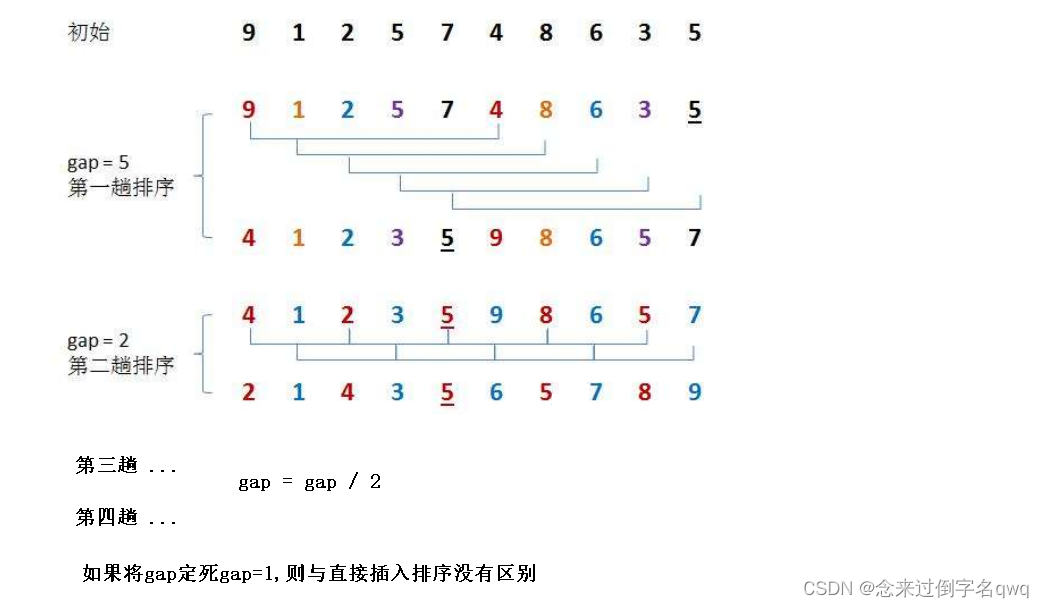
3. 希尔排序(Shell Sort)
希尔排序是直接插入排序的优化版,对于直接插入排序而言,数据越有序,排序越快,希尔排序正是借助直接插入排序的特点进行了优化。
思想:先对数据分组进行几次预排序(对数据分组进行直接插入排序),使数据形成较为有序的情况,最后整体进行一趟直接插入排序即可完成排序。
void ShellSort(int* a, int n)
{int gap = n; while (gap > 1) {gap = gap / 3 + 1; // gap / 2也可for (int j = 0; j < n - gap; ++j) {int end = j;int insertVal = a[end + gap];while (end >= 0 && insertVal < a[end]) {a[end + gap] = a[end];end -= gap;}a[end + gap] = insertVal;}}
}
-
希尔排序不好计算确切的时间复杂度,有牛人通过大量实验证明平均时间复杂度大致为O(n^1.3),比O(n*logn)要慢一点点,但两者差不多是同一量级。
-
gap>1时是预排序,gap=1时等于直接插入排序。
-
gap的取值,gap/2或gap/3+1是当前主流,也被认为是gap最好的取值。gap相当于划分多少组进行预排序,如果定死gap=1则与直接插入排序无异。gap/2或gap/3+1则是划分每组多少个数进行预排序,gap/3+1中的+1是因为要保证最后一组排序时gap=1进行直接插入排序操作。严格来说只要能保证最后一趟gap=1,无论gap除以几加几,都算是希尔排序。
-
每一组预排序后,都会逐渐加大数据的有序情况。后面几组预排序虽然每组划分的数据多了(gap逐渐减小间隔变小了),也就是比较次数变多了,但经过前面的预排序后数据渐渐有序,实际不会进行过多的比较挪数据操作,每前一次预排序都为后一次预排序减轻压力。
速度对比(毫秒):

4. 直接选择排序(Selection Sort)
每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,逐步向后存放。
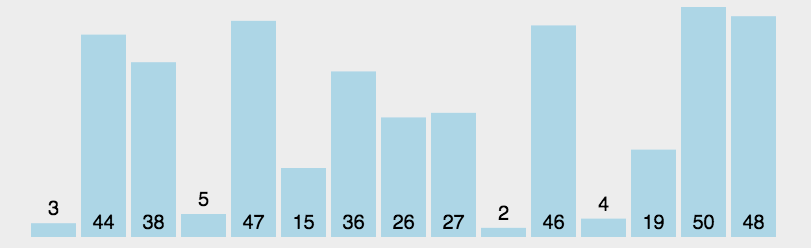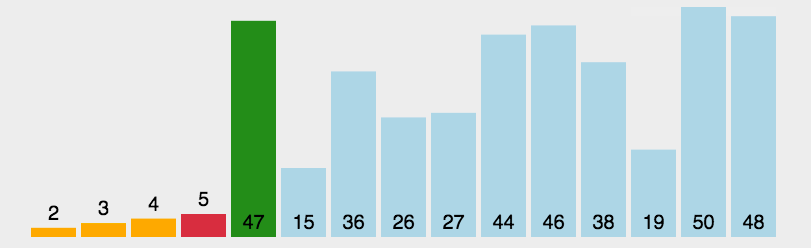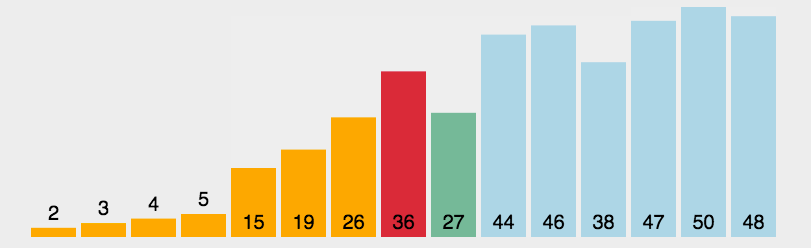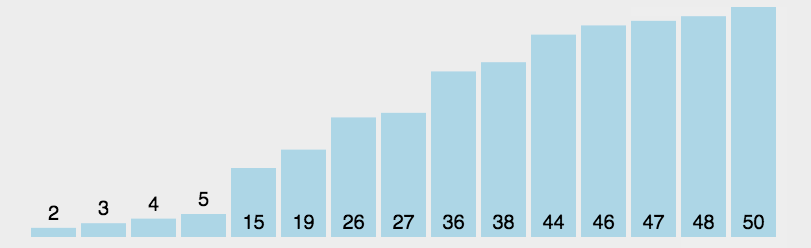

数据较为有序的情况下,直接选择排序选要比冒泡、直接插入排序慢。
void SelectionSort(int* a, int n)
{int begin = 0, end = n - 1;while (begin < end){int min = begin, max = end;for (int i = begin; i <= end; ++i){if (a[i] < a[min]) min = i;if (a[i] > a[max]) max = i;}Swap(&a[begin], &a[min]);if (max == begin){max = min;}Swap(&a[end], &a[max]);++begin; --end;}
}
在优化版中,必须有这样一个判断max==begin,并更新max的下标值!最小的数a[min]换到了左边begin位置,如果最大的数的下标max正好等于begin,那就出现这种问题:最大的数a[max]已经被换到min下标位置了,即a[min]才是最大数;而本来a[max]是最大的数,由于max==begin,而经过前面a[begin]与a[min]交换的影响,导致a[begin]/a[max]变成了最小的数,不加判断并更新max的后果是把最小的数放在右边end位置了。
5. 堆排序(Heap Sort)
了解堆请看:文章 堆 / 堆排序 / TopK问题(Heap)
时间复杂度O(nlog2n),排序速度与希尔差不多。也可以向上调整建堆,但比向下调整建堆要慢一些。
void HeapSort(int* a, int n)
{for (int parent = (n - 1 - 1) / 2; parent >= 0; --parent) {AdjustDown(a, n, parent);}for (int end = n - 1; end > 0; --end){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);}
}
/* 将堆向下调整为大堆 */
void AdjustDown(int* a, int size, int parent)
{int child = parent * 2 + 1; // 选出较大子节点child = child + 1 < size && a[child + 1] > a[child]? child + 1 : child;while (child < size && a[child] > a[parent]){Swap(&a[child], &a[parent]);parent = child; // 重复往下child = parent * 2 + 1;child = child + 1 < size && a[child + 1] > a[child]? child + 1 : child;}
}
parent初始为最后一个非叶子节点(多一个 -1 的原因),
向下调整(建大堆),往堆顶方向走把所有非叶子结点调整一遍。
堆顶最大值与堆底较小值交换,然后排除这个堆底的最大值(a[end]),
剩下的作为堆,从堆顶较小值开始向下调整为大堆(–end一步步排除新的最大值a[end])。
10w个数据,排序速度对比:

堆排序时间复杂度严格来算:
- 向上调整建堆O(nlogn) + 排序O(nlong):O(2n*2logn)。
- 向下调整调整建堆O(n) + 排序O(nlogn):O(2n*logn)。
所以说希尔排序O(n1.3)比O(n*log2n)要慢些,但却是同一量级。不过堆排序的时间复杂度严格来说比真正的O(nlog2n)要慢一点点,所以希尔排序与堆排序的速度相同。
6. 快速排序(Quick Sort)
快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法。
6.1 hoare快排(最早的快排方法)
基本思想:取待排序数据中的某个元素作为基准值,将数据分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后左右子序列重复该过程进行分割,直到所有元素都排列在相应位置上为止。
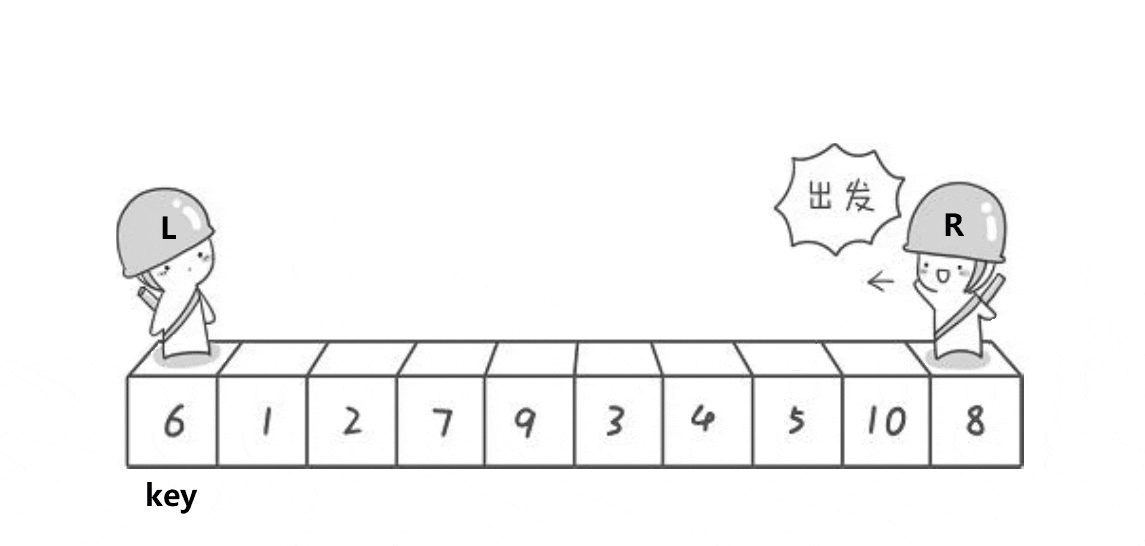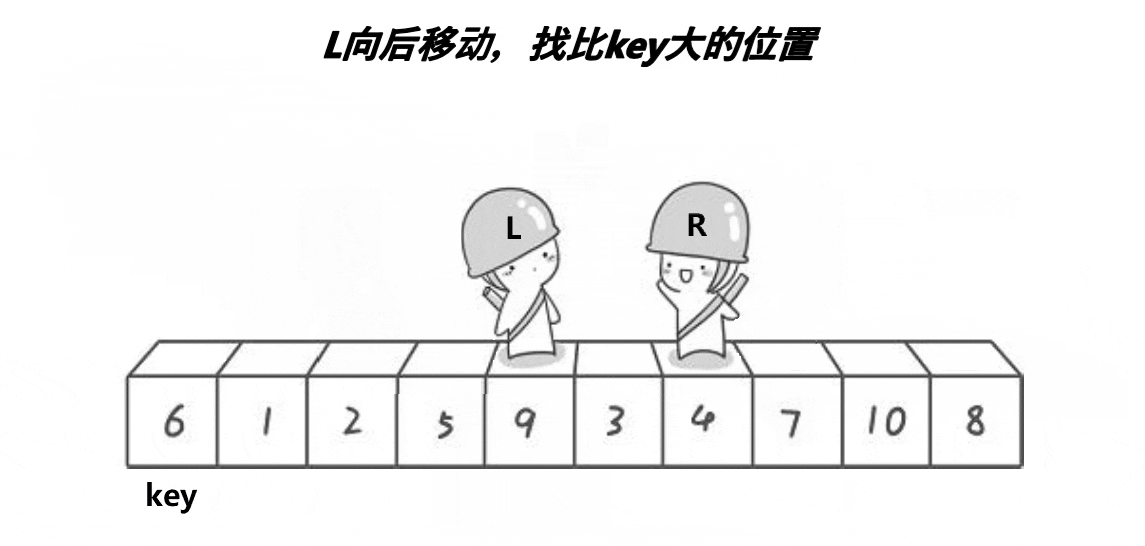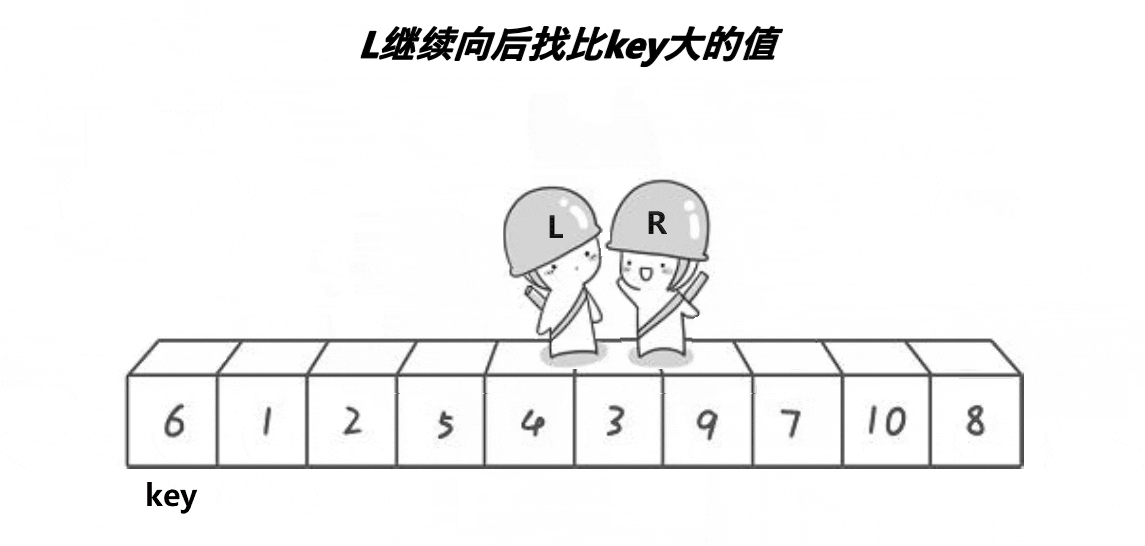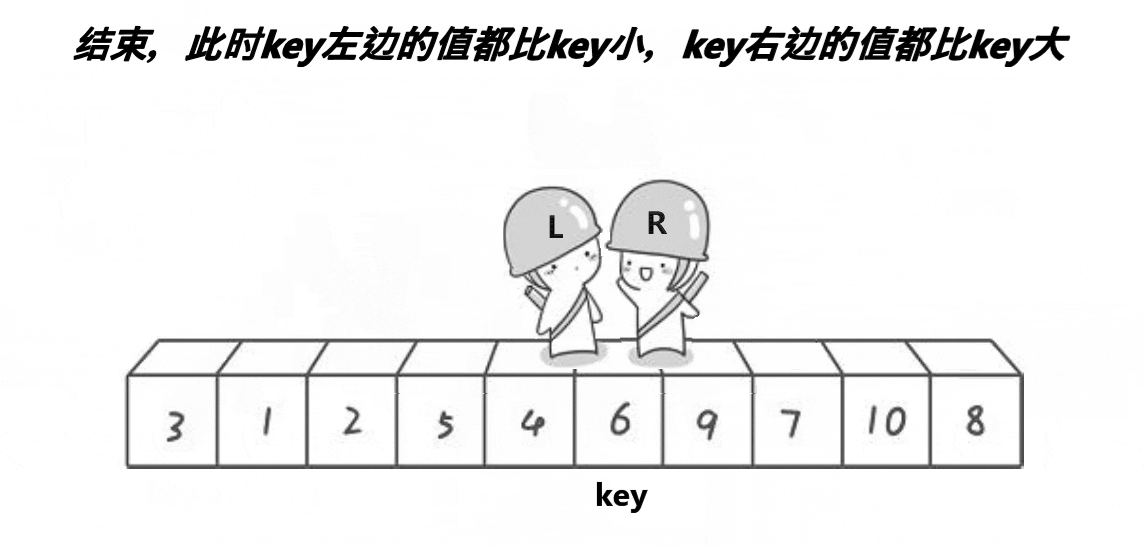
// 1.hoare递归(最早的快排方法)
void QuickSort1(int* a, int begin, int end)
{if (begin < end) {int left = begin;int right = end;int keyi = begin; // 基准值(下标)while (left < right) { /* 必须加上left<right防止内循环越界;>=而不是>,<=而不是<,防止重复值死循环。*/while (left < right && a[right] >= a[keyi]) {--right; // 找小的}while (left < right && a[left] <= a[keyi]) {++left; // 找大的}Swap(&a[left], &a[right]);}Swap(&a[left], &a[keyi]);QuickSort0(a, begin, left - 1); // 左区间序列QuickSort0(a, left + 1, end); // 右区间序列}
}
基准值的取法:
- 取序列第一个数据,需要右指针right先走(学习时往往采用的方式,上面动图演示也是基于这个方式);或取序列最后一个数据,需要左指针left先走(本质与前者没区别)。
- 三位取中法:key、left和right中取第二大的值作为基准值。(这是优化版,推荐)
优化快排(重要)
1. 减少函数递归的栈帧开销(虽然不用,但必须了解)
优化hoare快排的递归开销:递归树最后两三层(小区间)改用插入排序,减少大量函数栈帧内存消耗。该优化在debug环境下确实能优化,在逻辑上也确实能优化,但release环境同样也对递归进行了优化,而且优化力度只会更大,所以小区间使用插入排序减少递归栈帧的优化方案或许起不到效果。
例如一颗满二叉树,可以看到最后两三层的数量是最多的:
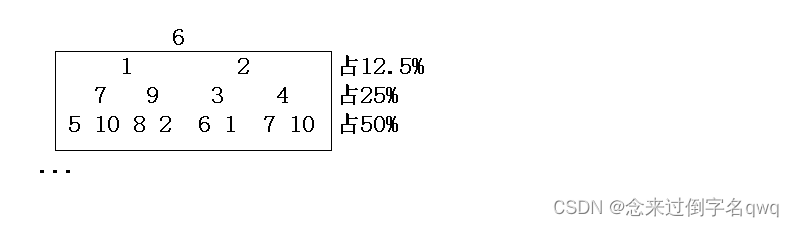
对于hoare快排划分左右区间同理:

#define RECUR_MAX 10
void QuickSortX(int* a, int begin, int end)
{if (begin < end){if (end - begin + 1 <= RECUR_MAX){InsertionSort(a, end - begin + 1);}else{int left = begin;int right = end;int keyi = begin; // 基准值(下标)while (left < right){ /* 必须加上left<right防止内循环越界;>=而不是>,<=而不是<,防止重复值死循环。*/while (left < right && a[right] >= a[keyi]) {--right; // 找小的}while (left < right && a[left] <= a[keyi]) {++left; // 找大的}Swap(&a[left], &a[right]);}Swap(&a[left], &a[keyi]);QuickSort0(a, begin, left - 1); // 左区间序列QuickSort0(a, left + 1, end); // 右区间序列}}
}
2.三位取中法取基准值(重点)
该优化提升非常大,主要是优化对较为有序的数据进行排序的情况。先看例子:一个较为有序的序列 1 2 3 4 7 6 8 10 9 对于这组数据,对于现在没有使用三位取中的快排而言,前面几趟排序是比较难受的。
比如第一趟,right一直不到比key要大的值,找最后搞得–right来到了key的位置,这就导致没有左区间,右区间从2开始,数据越是有序,快排速度越慢,最慢时退化到O(n2)。
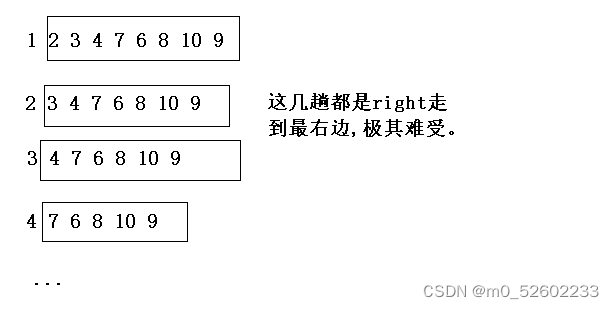
解决办法就是不要直接取第一位作为基准值,从begin、mid和end之间选出第二大的值作为基准值。

每趟排序前先三位取中做交换,这样就不至于面对这种情况,每趟排序right都走到最右边。
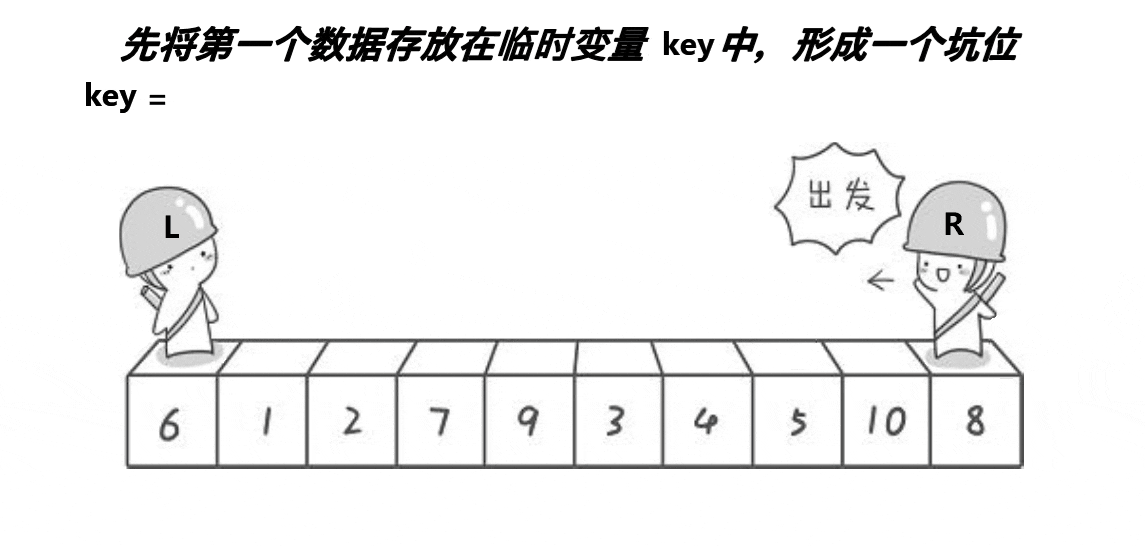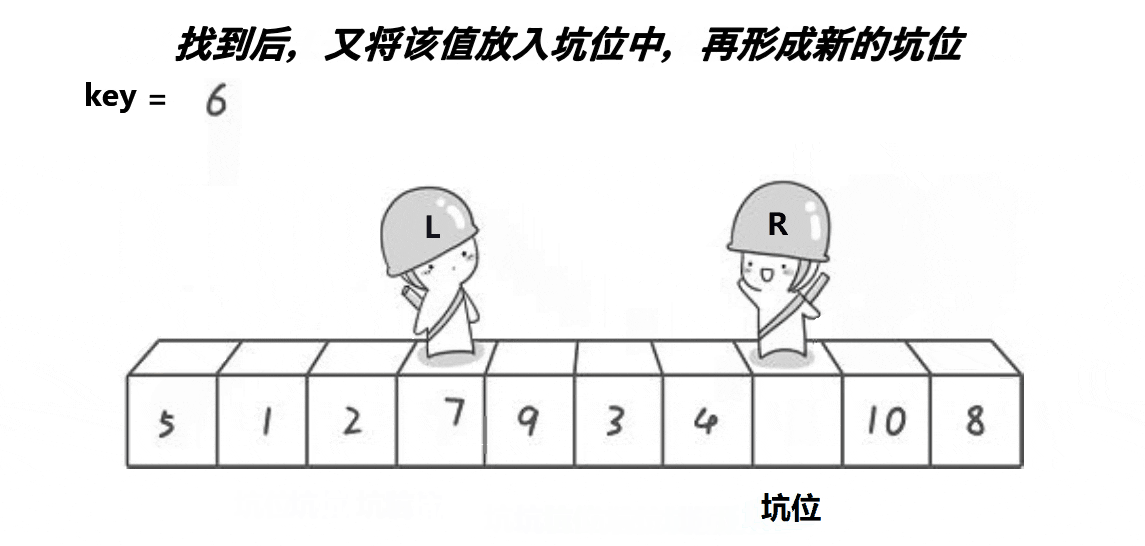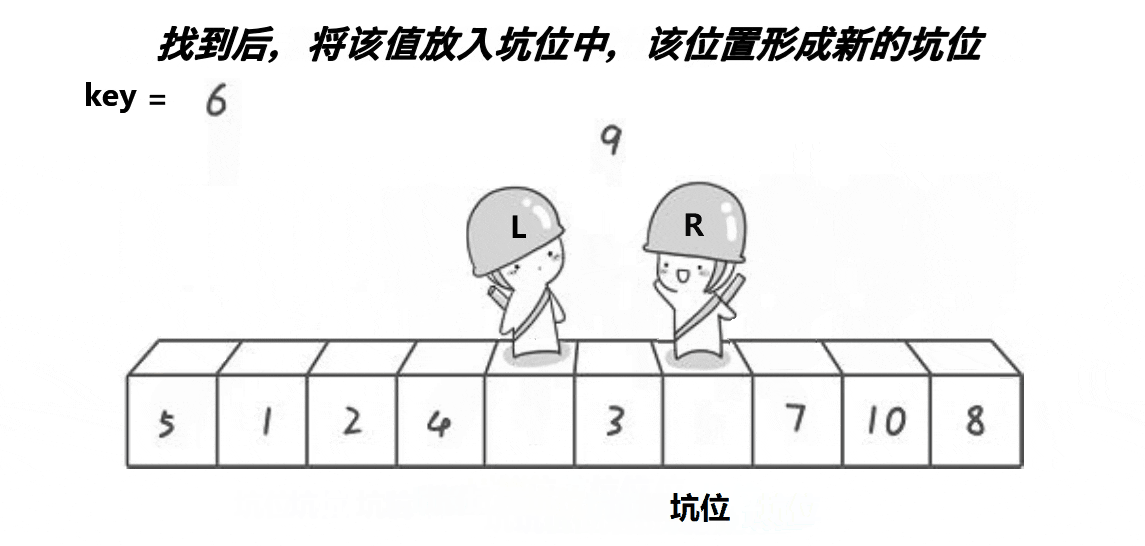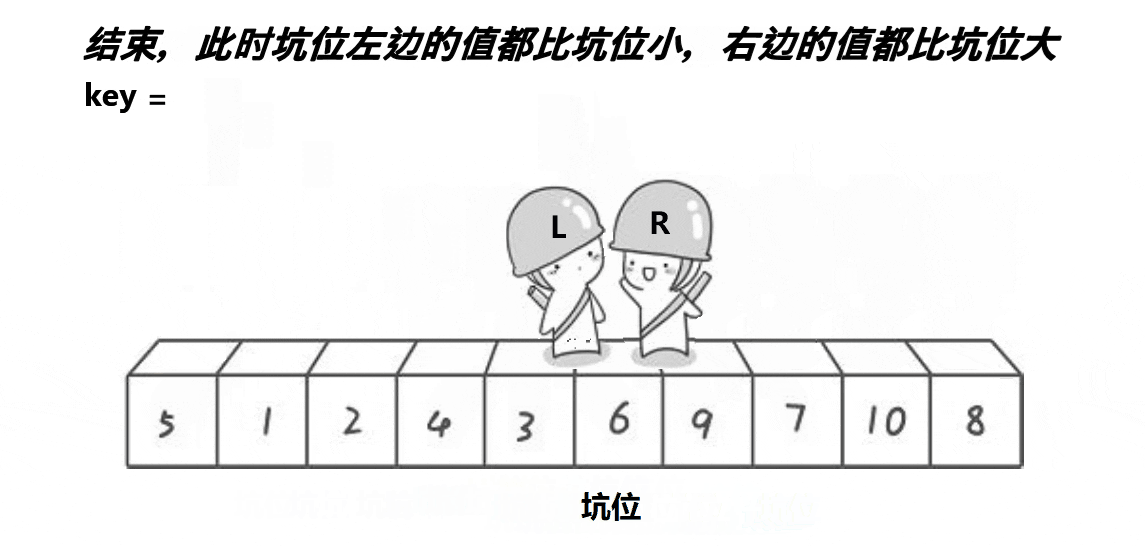
6.2 挖坑法快排
该方法思想与hoare版差不多,算是hoare版的改进,可能更好理解一些,但排序速度比起hoare版没啥大变化,差不多。
void QuickSort2(int* a, int begin, int end)
{if (begin < end){if ((end - begin) + 1 <= RECUR_MAX) {InsertionSort(a + begin, (end - begin) + 1);}else{int midi = MidIndex(a, begin, end);Swap(&a[begin], &a[midi]);int left = begin;int right = end;int key = a[begin];int pos = begin;while (left < right){while (left < right && a[right] >= key) {--right;}a[pos] = a[right];pos = right;while (left < right && a[left] <= key) {++left;}a[pos] = a[left];pos = left;}a[pos] = key;QuickSort2(a, begin, pos - 1);QuickSort2(a, pos + 1, end);}}
}
6.3 双指针法快排
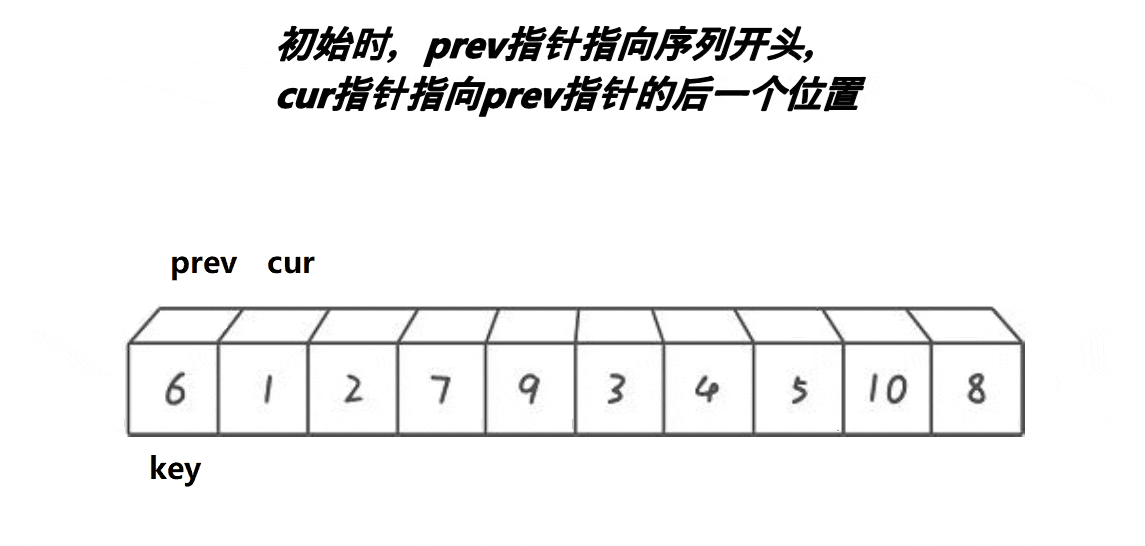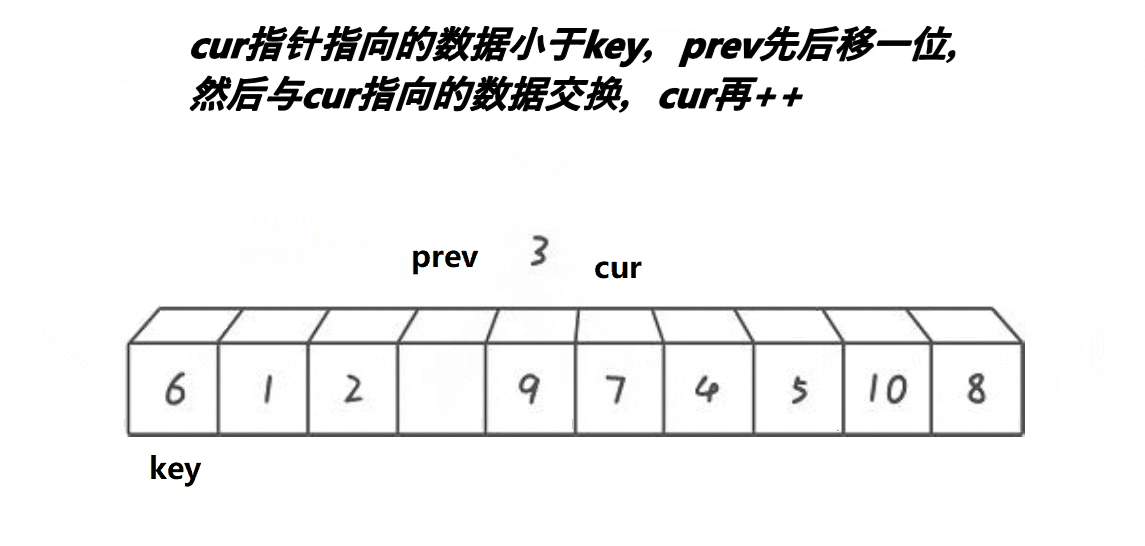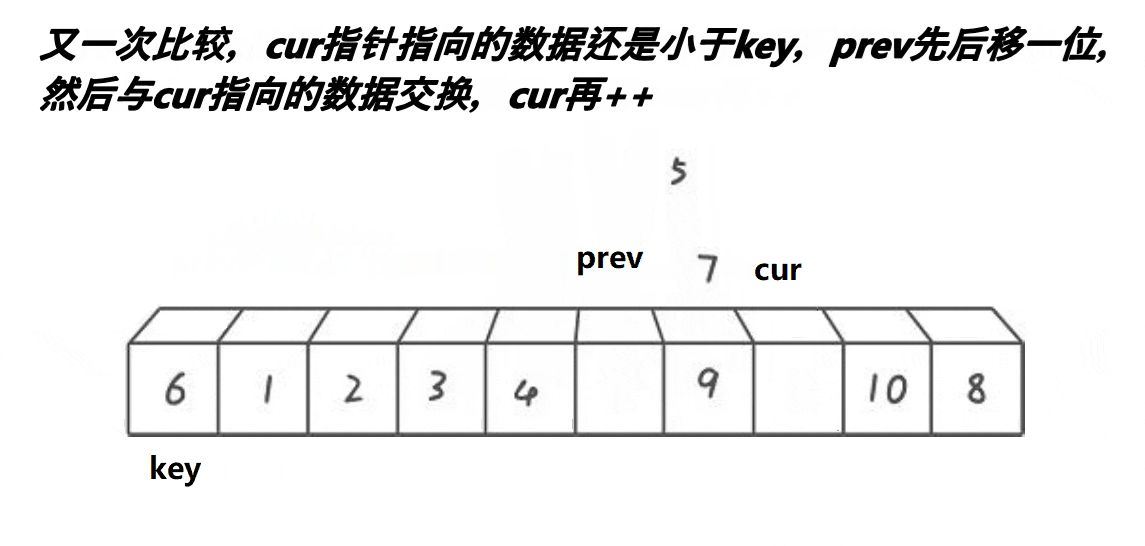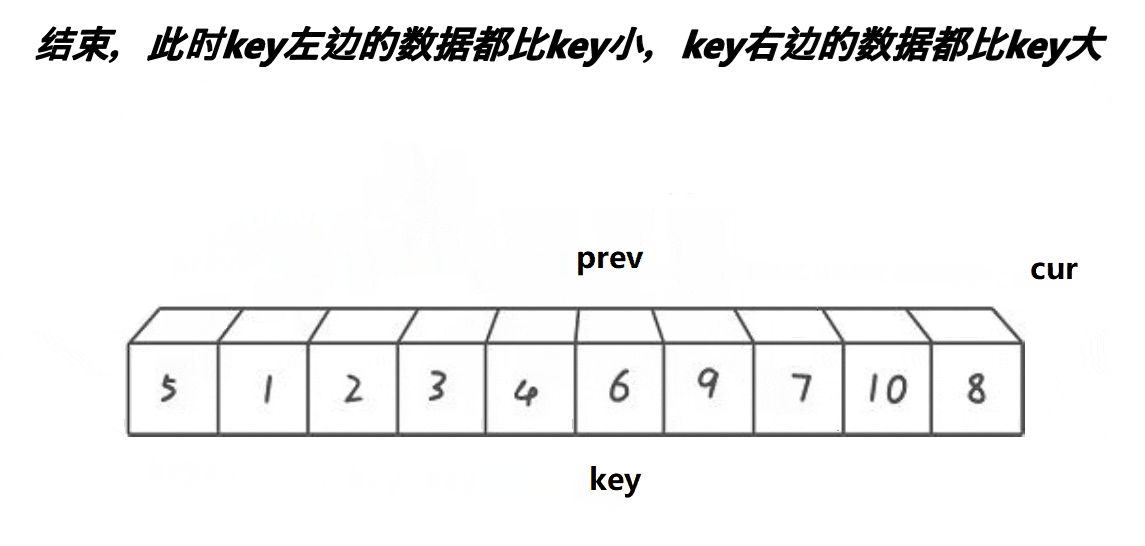
void QuickSort3(int* a, int begin, int end)
{if (begin < end){int midi = MidIndex(a, begin, end);Swap(&a[begin], &a[midi]);int keyi = begin;int pre = begin;int cur = begin + 1;while (cur <= end){if (a[cur] <= a[keyi]) {++pre;Swap(&a[pre], &a[cur]);}++cur;}Swap(&a[keyi], &a[pre]);keyi = pre;QuickSort3(a, begin, keyi - 1);QuickSort3(a, keyi + 1, end);}
}
6.4 非递归快排
需要借助栈(Stack),本质与递归一样,递归也是栈帧的开辟与销毁。
void QuickSortNonRecur(int* a, int begin, int end)
{assert(begin < end);Stack stack;Init(&stack);Push(&stack, begin); Push(&stack, end);// 类似递归while (!Empty(&stack)){// 出栈int right = Top(&stack); Pop(&stack);int left = Top(&stack); Pop(&stack);if (left < right){// 一趟快排int keyi = left;int previ = left;int curi = left + 1;while (curi <= right){if (a[curi] <= a[keyi]){++previ;Swap(&a[previ], &a[curi]);}++curi;}Swap(&a[keyi], &a[previ]);keyi = previ;// 入栈if (left < keyi - 1){Push(&stack, left);Push(&stack, keyi - 1);}if (keyi + 1 < right){Push(&stack, keyi + 1);Push(&stack, right);}}}Destroy(&stack);
}
快速排序的排序速度比较(包含测试代码)
单位为毫秒。
500w个数据:
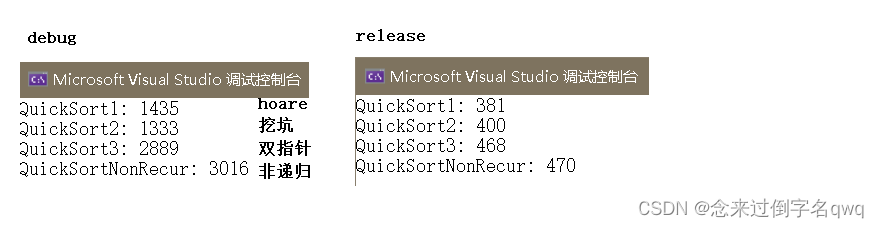
1000w个数据:
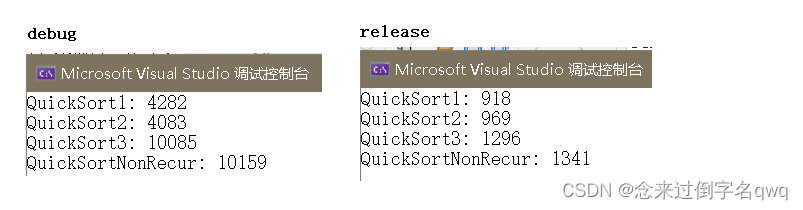
#include "Sort.h"void TestPerformance();int main() {TestPerformance();
}void TestPerformance() {const int N = 10000000;//int* a1 = (int*)malloc(sizeof(int) * N);//int* a2 = (int*)malloc(sizeof(int) * N);int* a3 = (int*)malloc(sizeof(int) * N);//int* a4 = (int*)malloc(sizeof(int) * N);int* a5 = (int*)malloc(sizeof(int) * N);int* a6 = (int*)malloc(sizeof(int) * N);int* a10 = (int*)malloc(sizeof(int) * N);int* a11 = (int*)malloc(sizeof(int) * N);int* a12 = (int*)malloc(sizeof(int) * N);srand((unsigned int)time(0));for (int i = 0; i < N; i++) {//a1[i] = rand();//a2[i] = a1[i];a3[i] = rand();//a4[i] = a1[i];a5[i] = a3[i];a6[i] = a3[i];a10[i] = a3[i];a11[i] = a3[i];a12[i] = a3[i];}//int begin1 = clock();//BubbleSort(a1, N);//int end1 = clock();//int begin2 = clock();//InsertionSort(a2, N);//int end2 = clock();int begin3 = clock();ShellSort(a3, N);int end3 = clock();//int begin4 = clock();//SelectionSort(a4, N);//int end4 = clock();int begin5 = clock();HeapSort(a5, N);int end5 = clock();int begin6 = clock();QuickSort1(a6, 0, N - 1);int end6 = clock();int begin10 = clock();QuickSort2(a10, 0, N - 1);int end10 = clock();int begin11 = clock();QuickSort3(a11, 0, N - 1);int end11 = clock();int begin12 = clock();QuickSort3(a12, 0, N - 1);int end12 = clock();//printf("BubbleSort: %d\n", end1 - begin1);//printf("InsertionSort: %d\n", end2 - begin2);printf("ShellSort: %d\n", end3 - begin3);//printf("SelectionSort: %d\n", end4 - begin4);printf("HeapSort: %d\n", end5 - begin5);printf("QuickSort1: %d\n", end6 - begin6);printf("QuickSort2: %d\n", end10 - begin10);printf("QuickSort3: %d\n", end11 - begin11);printf("QuickSortNonRecur: %d\n", end12 - begin12);
}7. 归并排序(Merge Sort)
7.1 递归版
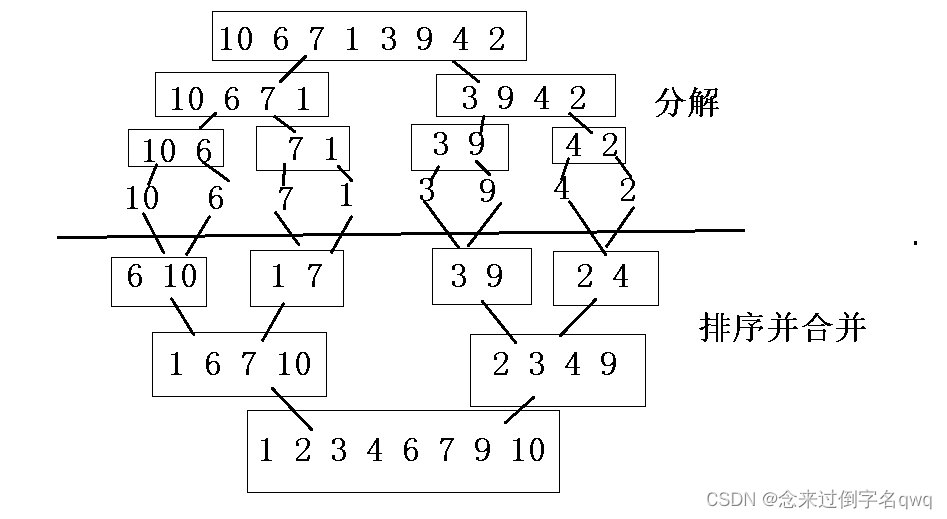
思想:分治法(Divide and Conquer),递归分治后小规模两两排序,逐渐合并大规模两两排序,最后到两个子序列合并成一个有序列表,该方法也称“二路归并”,时间复杂度为O(nlogn)。
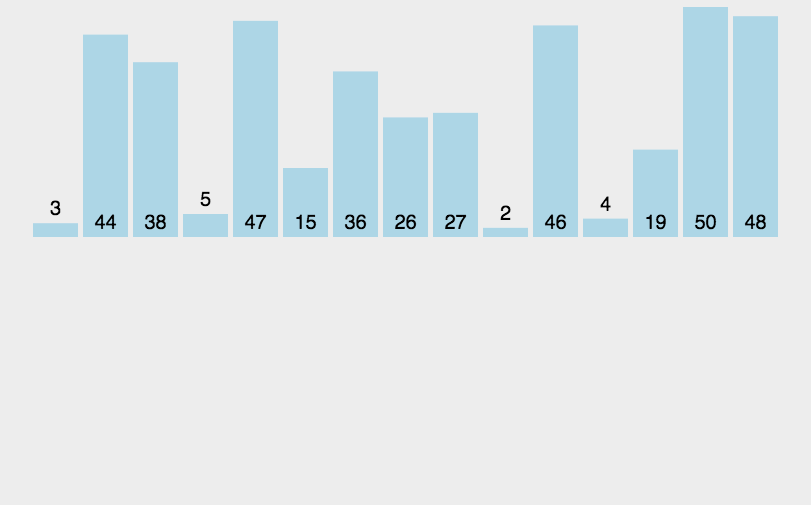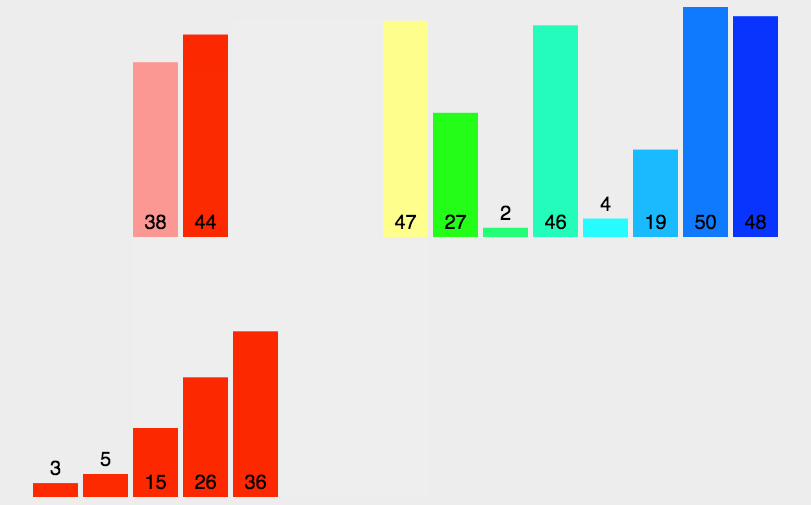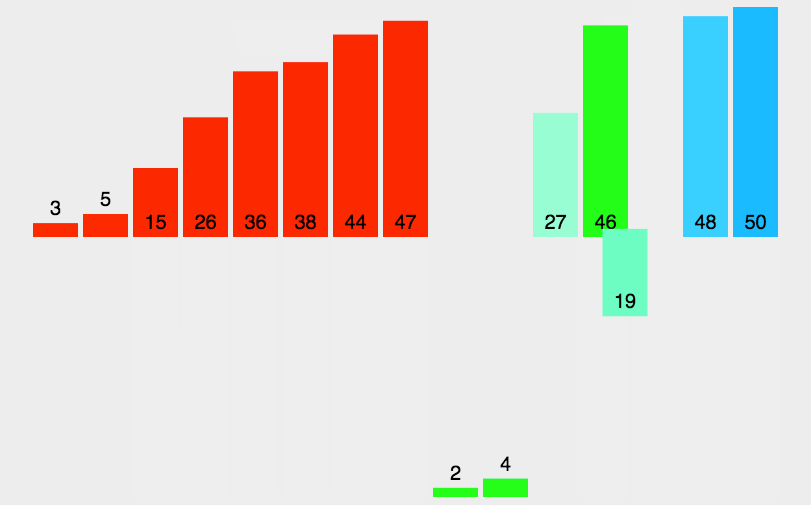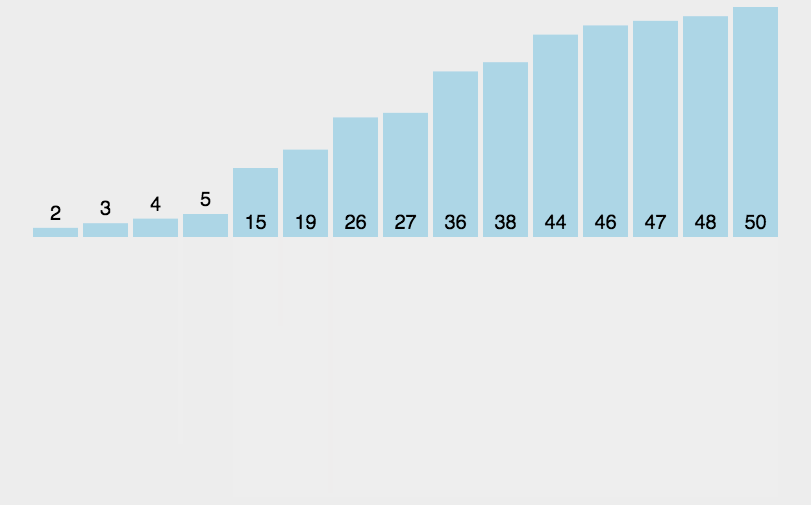
归并排序需要借助一个额外的数组,因此空间复杂度为O(n),在这个临时数组中排好序后,将排好序的数据复制回原序列。
// 二路归并排序
void Merge(int* a, int begin, int end, int* tmpArr);
void MergeSort(int* a, int begin, int end)
{if (begin < end){int* tmpArr = (int*)malloc(sizeof(int) * (end + 1));if (tmpArr == NULL){perror("MergeSort malloc failed.");return;}Merge(a, begin, end, tmpArr);free(tmpArr);tmpArr = NULL;}
}
void Merge(int* a, int begin, int end, int* tmpArr)
{// 分解int mid = (begin + end) / 2;if (begin < end){Merge(a, begin, mid, tmpArr);Merge(a, mid + 1, end, tmpArr);}// 排序,合并存入临时数组int begin1 = begin;int begin2 = mid + 1;int k = begin;while (begin1 <= mid && begin2 <= end){if (a[begin1] < a[begin2]) tmpArr[k++] = a[begin1++];elsetmpArr[k++] = a[begin2++];}// 两个序列中某一个可能有剩余while (begin1 <= mid) {tmpArr[k++] = a[begin1++];}while (begin2 <= end) {tmpArr[k++] = a[begin2++];}// 临时数组中排好序的数组,拷贝回原数组for (int i = begin; i <= end; i++) {a[i] = tmpArr[i];}
}
归并排与快排的排序速度比较:

7.2 非递归版
void MergeSortNonRecur(int* a, int n)
{int* tmpArr = (int*)malloc(sizeof(int) * n);if (tmpArr == NULL){perror("MergeSortNonRecur malloc failed.");return;}// gap:区间间隔for (int gap = 1; gap < n; gap *= 2){for (int i = 0; i < n; i += 2 * gap){// 划区间int begin1 = i;int end1 = i + gap - 1;int begin2 = i + gap;int end2 = i + (2 * gap) - 1;// 处理可能越界的区间if (end2 >= n) {end2 = n - 1;}if (end1 >= n || begin2 >= n) {break;}// 排序int k = begin1;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2])tmpArr[k++] = a[begin1++];elsetmpArr[k++] = a[begin2++];}// 两个序列中某一个可能有剩余while (begin1 <= end1) {tmpArr[k++] = a[begin1++];}while (begin2 <= end2) {tmpArr[k++] = a[begin2++];}// 临时数组中排好序的数组,拷贝回原数组for (int j = i; j <= end2; ++j) {a[j] = tmpArr[j];}}}
}
8. 计数排序
特点:效率极高。
缺点:适用范围有限,小数、结构体数据无法排序。
时间复杂度:O(MAX(n, range)),range = max - min(最大值-最小值)。
空间复杂度:O(range)。
计数排序是稳定排序算法。
排序思想:需要借助一个临时数组,在临时数组中统计原数组中每个值出现的次数。
void CountSort(int* a, int n)
{int min = a[0];int max = a[0];for (int i = 0; i < n; ++i){if (a[i] < min) {min = a[i];}if (a[i] > max) {max = a[i];}}int range = max - min + 1;int* count = (int*)calloc(range, sizeof(int));if (count == NULL){perror("CountSort malloc failed.");return;}// 计数for (int i = 0; i < n; ++i){count[a[i] - min]++;}// 排序int k = 0;for (int i = 0; i < range; ++i){for (int j = 0; j < count[i]; ++j){a[k++] = i + min;}}
}相关文章:

【数据结构与算法】常见排序算法(Sorting Algorithm)
文章目录 相关概念1. 冒泡排序(Bubble Sort)2. 直接插入排序(Insertion Sort)3. 希尔排序(Shell Sort)4. 直接选择排序(Selection Sort)5. 堆排序(Heap Sort)…...

Unity3D学习之XLua实践——背包系统
文章目录 1 前言2 新建工程导入必要资源2.1 AB包设置2.2 C# 脚本2.3 VSCode 的环境搭建 3 面板拼凑3.1 主面板拼凑3.2 背包面板拼凑3.3 格子复合组件拼凑3.4 常用类别名准备3.5 数据准备3.5.1 图集准备3.5.2 json3.5.3 打AB包 4 Lua读取json表及准备玩家数据5 主面板逻辑6 背包…...

前端技术研究越深入,越觉得技术不是决定录用唯一条件。
一、拒绝抬杠 我说技能不是唯一条件,不是说技能不重要,招聘前端条件是1X,其中1是技能,X是其他条件。 如果X条件很优秀,1这个条件可以降格为0.8、0.5,甚至更低。 有人就抬杠,那为啥不招聘清洁工来干前端&…...

vue组件的重新渲染的问题
目录 1.方式1 2.方式2 1.方式1 修改组件上的key属性 Vue是通过diffing算法比较虚拟DOM和真实DOM,来判断新旧 DOM 的变化。key是虚拟DOM对象的标识,在更新显示时key表示着DOM的唯一性。 DOM是否变化的核心是通过判断新旧DOM的key值是否变化,…...
opengl 学习(二)-----你好,三角形
你好,三角形 分类demo效果解析 分类 opengl c demo #include "glad/glad.h" #include "glfw3.h" #include <iostream> #include <cmath> #include <vector>using namespace std;/** * 在学习此节之前,建议将这…...

mongodb4.2升级到5.0版本,升级到6.0版本, 升级到7.0版本案例
今天一客户想把自己当前使用的mongodb数据库4.2版本升级到7.0版本。难道mongodb能直接跳跃升级吗? 经过几经查找资料,貌似真不行呀。确定升级流程如下: 还得从mongo4.2升级到5.0。其次再从5.0升级到6.0。最后再从6.0升级到7.0。 开始升级之前将数据进行备份 这一步…...

CPU处理器模式与异常
ARM架构中的Exception Level(EL) 在ARM架构中,Exception Level(EL)是一个关键概念,它表示了处理器当前处理异常或中断的层次。ARMv8-A架构定义了四个Exception Levels:EL0、EL1、EL2和EL3&…...

Day 53 |● 1143.最长公共子序列 ● 1035.不相交的线 ● 53. 最大子序和
1143.最长公共子序列 class Solution { public:int longestCommonSubsequence(string text1, string text2) {vector<vector<int>> dp(text1.size()1,vector<int>(text2.size()1,0));int res 0;for(int i 1; i < text1.size(); i){for(int j 1; j <…...

ant-desgin charts双轴图DualAxes,柱状图无法立即显示,并且只有在调整页面大小(放大或缩小)后才开始显示
摘要 双轴图表中,柱状图无法立即显示,并且只有在调整页面大小(放大或缩小)后才开始显示 官方示例代码 在直接复制,替换为个人数据时,出现柱状图无法显示问题 const config {data: [data, data],xFiel…...
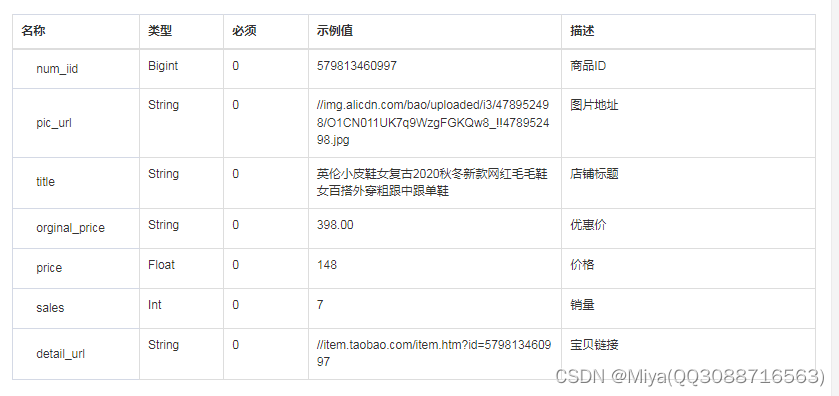
获取别人店铺的所有商品API接口
使用淘宝淘口令接口的步骤通常包括: 注册成为淘宝开放平台的开发者:在淘宝开放平台网站上注册账号并完成认证。 创建应用以获取API密钥:在您的开发者控制台中创建一个应用,并获取用于API调用的密钥,如Client ID和Clie…...

成都正信:亲戚借了钱一直不还怎么委婉的说
在中国传统文化中,亲情关系往往被视为最为重要和敏感的部分。当亲戚间发生借贷时,若出现拖欠不还的情形,处理起来尤为棘手。面对这样的尴尬局面,采取委婉而有效的沟通方式至关重要。 张华最近就遇到了这样的困扰。他的表弟去年因急…...
Truenas入门级教程
Truenas入门教程 前言:系统相关配置 采用I3 4160,采用了2块500G的硬盘,内存为8G,两个网卡只用了其中一个,系统安装的是core版本 硬件采用DELL3020MT机箱,自带3个SATA网口,后期网口不够&#…...
 over(条件))
窗口函数dense() over(条件)
力扣题目连接 https://leetcode.cn/problems/rank-scores/ 在 SQL 中,DENSE_RANK() 是一个窗口函数,用于计算结果集中每行的稠密排名(dense rank)。DENSE_RANK() 函数会为具有相同排序字段值的行分配相同的排名,但不会…...

蓝牙APP开发实现汽车遥控钥匙解锁汽车智能时代
在现代社会,随着科技的不断发展,汽车已经不再是简单的交通工具,而是与智能科技紧密相连的载体。其中,通过开发APP蓝牙程序实现汽车遥控钥匙成为了一种趋势,为车主带来了便捷与安全的体验。虎克技术公司作为行业领先者&…...
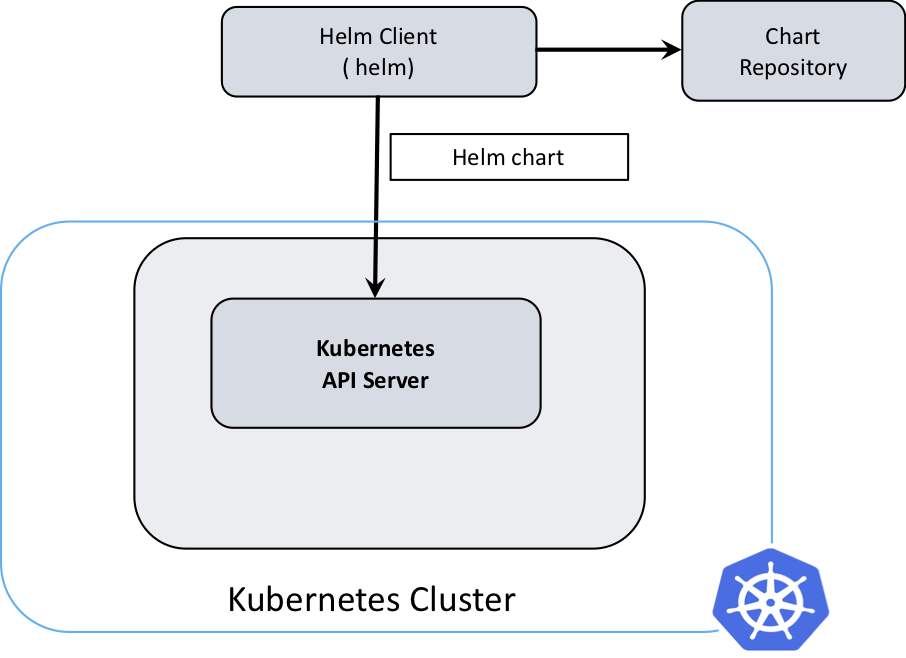
第三天 Kubernetes进阶实践
第三天 Kubernetes进阶实践 本章介绍Kubernetes的进阶内容,包含Kubernetes集群调度、CNI插件、认证授权安全体系、分布式存储的对接、Helm的使用等,让学员可以更加深入的学习Kubernetes的核心内容。 ETCD数据的访问 kube-scheduler调度策略实践 预选与…...

redis小结
1.mysql是数据库,redis是数据库,那么什么时候使用应该使用哪种数据库? redis做缓存是为了缓解mysql的压力,在数据库表数据量上千万,并且访问频繁时,mysql压力增大,在有索引的情况下依旧效果不佳,需要使用…...

PHP伪协议详解
PHP伪协议详解 一、前言1.什么是PHP伪协议?2.什么时候用PHP伪协议? 二、常见的php伪协议php://inputphp://filterzip://与bzip2://与zlib://协议data://phar:// 一、前言 1.什么是PHP伪协议? PHP伪协议是PHP自己支持的一种协议与封装协议,…...
进程:守护进程
一、守护进程的概念 守护进程是脱离于终端控制,且运行在后端的进程。(孤儿进程)守护进程不会将信息显示在任何终端上影响前端的操作,也不会被终端产生的任何信息打断,例如(ctrlc).守护进程独立…...

千里马平台项目管理理念
软件项目的成功和失败和技术关系不大,尤其是应用型软件,不可能有技术难关卡死了项目,大部分问题还是出现在项目管理层面。公司的业务形态是帮助客户构建自己的信息化生态圈,项目管理咨询也是其中的核心内容。 我们的软件项目管理理…...

GB 2312字符集:中文编码的基石
title: GB 2312字符集:中文编码的基石 date: 2024/3/7 19:26:00 updated: 2024/3/7 19:26:00 tags: GB2312编码中文字符集双字节编码区位码规则兼容性问题存储空间优化文档处理应用 一、GB 2312字符集的背景 GB 2312字符集是中国国家标准委员会于1980年发布的一种…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...
