【LeetCode】升级打怪之路 Day 14:二叉树的遍历
今日题目:
- 144. 二叉树的前序遍历
- 94. 二叉树的中序遍历
- 145. 二叉树的后序遍历
- 102. 二叉树的层序遍历
- 107. 二叉树的层序遍历 II
- 199. 二叉树的右视图
- 637. 二叉树的层平均值
- 429. N 叉树的层序遍历
- 515. 在每个树行中找最大值
- 116. 填充每个节点的下一个右侧节点指针
- 117. 填充每个节点的下一个右侧节点指针 II
- 104. 二叉树的最大深度
- 111. 二叉树的最小深度
目录
- Problem 1:二叉树的递归遍历 【easy】
- Problem 2:二叉树的迭代遍历 【classic】
- 2.1 前序遍历 迭代版
- 2.2 中序遍历 迭代版
- 2.3 后序遍历 迭代版 【必背】
- Problem 3:二叉树的层次遍历 【classic】
- LC 102. 二叉树的层序遍历
- 其他例题
今天主要学习了二叉树的递归遍历、迭代遍历和层序遍历,其中递归遍历和层序遍历都很简单,而迭代遍历的代码写起来稍有困难,这部分需要在理解的基础上,把伪代码背过。
Problem 1:二叉树的递归遍历 【easy】
递归遍历二叉树很简单了,可以拿这三个遍历题练练手:
- 144. 二叉树的前序遍历
- 94. 二叉树的中序遍历
- 145. 二叉树的后序遍历
Problem 2:二叉树的迭代遍历 【classic】
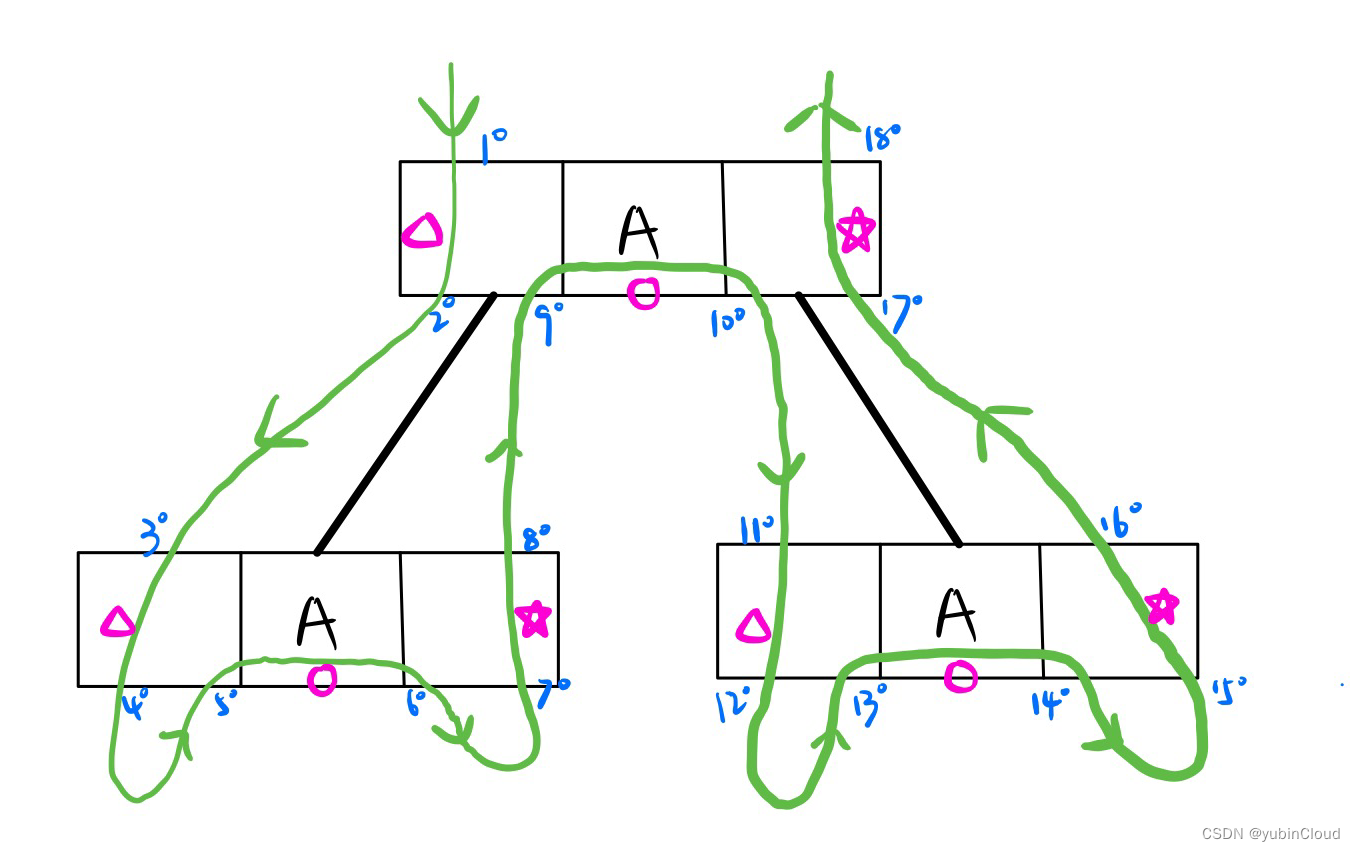
2.1 前序遍历 迭代版
144. 二叉树的前序遍历
伪代码思路:
void preOrder2(TreeNode T) {Stack S;TreeNode p = T;while (p !=null && !S.empty()) {if (p) {visit(p); // 第一次经过时访问之S.push(p); p = p.left(); // 一路向左} else {S.pop(p);p = p.right(); // 向右走(step 10)}}
}
Java 代码实现:
class Solution {public List<Integer> preorderTraversal(TreeNode root) {if (root == null) {return Collections.emptyList();}List<TreeNode> stack = new ArrayList<>();List<Integer> result = new ArrayList<>();TreeNode p = root;while (p != null || !stack.isEmpty()) {if (p != null) {result.add(p.val);stack.addLast(p);p = p.left;} else {p = stack.removeLast();p = p.right;}}return result;}
}
2.2 中序遍历 迭代版
94. 二叉树的中序遍历
伪代码如下:
void inOrder2(TreeNode T) {Stack S;TreeNode p = T; // p 是遍历指针while (p != null || !S.empty()) { // 栈不空或者 p 不空时循环// 一路向左直到空节点if (p) {S.push(p); // 当前节点入栈p = p.left; // 向左走}// 遇到空节点else {S.pop(p); // 访问栈顶元素(step9),由于接下来要访问之,故 popvisit(p); // 访问之p = p.right; // 向右子树走(step10)}}
}
2.3 后序遍历 迭代版 【必背】
145. 二叉树的后序遍历
这个建议直接背过,掌握这个算法思路后,并不难背,大不了多写几遍代码。
算法思路:① 一路向左走并入栈,直到空节点;② 碰到空节点后,读取栈顶元素但不弹出(step9):如果存在右孩子并且未访问过(为了确定之前是从左孩子返回过来的),则向右走;否则,栈顶元素出栈并访问之。
- 为了区分返回到一个节点时是从左子树回来的还是从右子树回来的,代码设定了辅助指针 recent,它指向最近访问过的节点,当 p.right != recent 时,表示这是从左子树回来的,还没有访问过右子树。
后序遍历迭代版特点:
- 当一个节点的左右子树都被访问后才能出栈(pop)。
- 实际上,当访问一个节点 p 时,栈中节点恰好是 p 节点的所有祖先,从栈底到栈顶再加上 p 节点,刚好构成从根节点到 p 节点的一条路径。很多算法设计都利用了这一思想,比如求根到某节点的路径,求两个节点的最近公共祖先等。
伪代码如下:
void postOrder2(TreeNode T) {Stack S;TreeNode p = T, recent = null;while (p != null && !S.empty()) {if (p) {S.push(p);p = p.left;} else { // 向右p = S.top(); // 读取栈顶节点if (p.right && p.right != recent) { // 若存在右孩子,且未被访问过p = p.right; // 向右走} else { // 否则弹出节点并访问之S.pop(p);visit(p);recent = p; // 更新最近访问的节点p = null; // 节点访问完后,重置 p 指针}} // end else} // end while
}
代码实现:
class Solution {public List<Integer> postorderTraversal(TreeNode root) {List<TreeNode> stack = new ArrayList<>();List<Integer> result = new ArrayList<>();TreeNode p = root, recent = null;while (p != null || !stack.isEmpty()) {if (p != null) {stack.addLast(p);p = p.left;} else {p = stack.getLast();if (p.right != null && recent != p.right) {p = p.right;} else {result.add(p.val);recent = p;stack.removeLast();p = null;}}}return result;}
}
Problem 3:二叉树的层次遍历 【classic】
层序遍历的模板可以解决一大类问题,需要谨记。
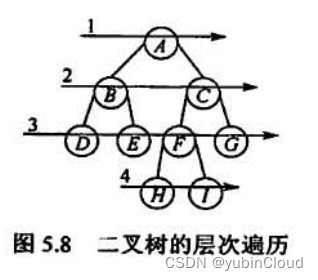
算法思想:
- 初始化一个辅助队列 Q;
- 根节点入队;
- 若 Q 非空,则队头节点出队并访问之,并将其左右孩子入队(如果有的话);
- 重复 3 直至队空。
伪代码实现:
void levelOrder(TreeNode T) {Queue Q; // 1. 初始化一个辅助队列TreeNode p;Q.offer(T); // 2. 根节点入队while (!Q.empty()) { // 3. 若 Q 非空,则int sz = Q.size(); // 这一层的节点个数// 依次将这一层的节点出队for (int i = 0; i < sz; i++) {var curr = Q.poll();visit(curr); // 访问之// 将左右子节点加入队列if (curr.left != null) {Q.offer(curr.left);}if (curr.right != null) {Q.offer(curr.right);}}} // 4. 重复直至队空return;
}
LC 102. 二叉树的层序遍历
102. 二叉树的层序遍历
这是经典使用层序遍历来获取二叉树的层序遍历顺序,基本与模板一致:
class Solution {public List<List<Integer>> levelOrder(TreeNode root) {if (root == null) {return Collections.emptyList();}Deque<TreeNode> queue = new LinkedList<>(); // 队列queue.addLast(root);List<List<Integer>> result = new ArrayList<>();while (!queue.isEmpty()) {int sz = queue.size();List<Integer> levelNums = new ArrayList<>();for (int i = 0; i < sz; i++) {var node = queue.removeFirst();levelNums.add(node.val);// 将左右子节点加入队列if (node.left != null) {queue.addLast(node.left);}if (node.right != null) {queue.addLast(node.right);}}result.add(levelNums);}return result;}
}
其他例题
借助二叉树的层序遍历的模板,可以一口气解决下面十个题目:
- 102. 二叉树的层序遍历
- 107. 二叉树的层序遍历 II
- 199. 二叉树的右视图
- 637. 二叉树的层平均值
- 429. N 叉树的层序遍历
- 515. 在每个树行中找最大值
- 116. 填充每个节点的下一个右侧节点指针
- 117. 填充每个节点的下一个右侧节点指针 II
- 104. 二叉树的最大深度
- 111. 二叉树的最小深度
相关文章:

【LeetCode】升级打怪之路 Day 14:二叉树的遍历
今日题目: 144. 二叉树的前序遍历94. 二叉树的中序遍历145. 二叉树的后序遍历102. 二叉树的层序遍历107. 二叉树的层序遍历 II199. 二叉树的右视图637. 二叉树的层平均值429. N 叉树的层序遍历515. 在每个树行中找最大值116. 填充每个节点的下一个右侧节点指针117. …...
[Unity实战]使用NavMeshAgent做玩家移动
其实除了Character Controller, Rigidbody,我们还可以使用NavMeshAgent去做。这么做的好处是能避免玩家去莫名其妙的地方(毕竟基于烘焙过的导航网格),一般常见于元宇宙应用和mmo。 根据Unity手册,NavMeshAgent 也有和…...

官网:随便搞个?那不如不搞,搞不好就给公司减分了。
官网建设确实需要认真对待,不能随便搞。一个粗制滥造的官网可能会给公司带来负面影响,降低品牌形象和用户体验。以下是一些官网建设的重要原则: 专业性:官网应该展示公司的专业性和专业知识。它应该以专业的设计、内容和功能来展示…...
Ansible 基础入门
2)Ansible 介绍 Ansible 基本概念 Ansible 是一种自动化运维工具,基于 Paramiko 开发的,并且基于模块化工作,Ansible 是一种集成 IT 系统的配置管理、应用部署、执行特定任务的开源平台,它是基于 Python 语言…...
讨论:5万官网是建站界的劳斯莱斯了吧,到了软件开发领域呢?
如题,所以赛道选择很重要,当然难度系数也不一样。能花5万元做官网的,凤毛麟角,如果是做软件开发,5万元顶多算个起步价,老铁们,是这样吗?...
手写分布式配置中心(三)增加实时刷新功能(短轮询)
要实现配置自动实时刷新,需要改造之前的代码。代码在https://gitee.com/summer-cat001/config-center 服务端改造 服务端增加一个版本号version,新增配置的时候为1,每次更新配置就加1。 Overridepublic long insertConfigDO(…...
【RabbitMQ】WorkQueue
📝个人主页:五敷有你 🔥系列专栏:MQ ⛺️稳中求进,晒太阳 Work Queues Work queues任务模型,简单来说就是让多个消费者绑定到一个队列,共同消费队列中的消息 当消息处理比较耗时的时候&…...

国内免费好用 Chat GPT推荐
无论您是寻找技术洞见还是灵感激发,此网站是您的绝佳去处。探索着名作家的精彩观点和创意解决方案,它不仅是知识的源泉,更是思维的驱动力。在这里,您将发现无尽的学习资源和启发,助您不断前行这是一款基于OpenAi开发的…...
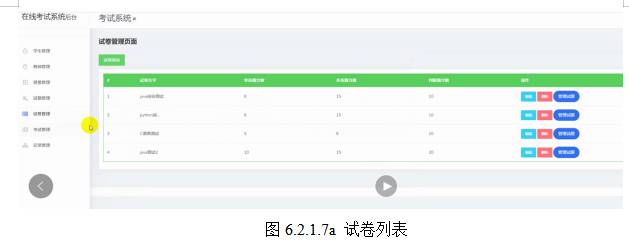
基于springboot实现在线考试系统项目【项目源码+论文说明】
基于springboot实现在线考试系统演示 摘要 时代在变化,科技技术以无法预测的速度在达到新的高度,并且被应用于社会生活的各个领域,随着生活的加快,也使很多潜在的点逐渐突显出来,社会对于人才的要总是非常迫切的&…...

golang中go build 后读取配置文件
golang打包后读取配置文件 在用go写代码的时候,为了好用经常使用go build 打包,如果我们用到了配置文件,就总是导致不能找到文件所在位置了出现bug,所以以下代码就解决了这个问题。 核心代码: file, err : exec.Look…...

为raspberrypi编译bpftrace调试工具
基于eBPF的嵌入式应用调试 笔者之前写过几篇有关于使用eBPF调试Linux内核和应用的博客,其中提到,在嵌入式设备上使用BCC或bpftrace是不可行的;主要原因在于嵌入式设备的资源有限,而这两个调试工具依赖python/clang/llvm等库&…...

分段线性化问题探析
目录 1 使用0-1变量将分段函数转换为线性约束 2 连续函数采用分段线性化示例 3 matlab程序测试 4 matlab测试结果说明 5 分段线性化应用 1 使用0-1变量将分段函数转换为线性约束 2 连续函数采用分段线性化示例 3 matlab程序测试 clc;clear all; gn10;tn1; x_pfsdpvar(1, t…...

从零学算法2917
2917.给你一个下标从 0 开始的整数数组 nums 和一个整数 k 。 nums 中的 K-or 是一个满足以下条件的非负整数: 只有在 nums 中,至少存在 k 个元素的第 i 位值为 1 ,那么 K-or 中的第 i 位的值才是 1 。 返回 nums 的 K-or 值。 注意 …...
[HackMyVM] 靶场 Wave
kali:192.168.56.104 主机发现 arp-scan -l # arp-scan -l Interface: eth0, type: EN10MB, MAC: 00:0c:29:d2:e0:49, IPv4: 192.168.56.104 Starting arp-scan 1.10.0 with 256 hosts (https://github.com/royhills/arp-scan) 192.168.56.1 0a:00:27:00:00:05 (Un…...

云渲染平台都开始涨价了?2024年性价比高的云渲染平台推荐
最近部分云渲染平台开始涨价,不论是通过调整机器性能,还是直接提价,都会对成本产生影响。这对已经习惯了平台价格的用户来说,并不是一件好事。这里举一些例子: 比如平台A,原“首小时渲染0.66元模式”已经下…...
)
搜索-BFS Meteor Shower S(流星雨)
Meteor Shower S(流星雨) 题目连接 题目描述 贝茜听说一场特别的流星雨即将到来:这些流星会撞向地球,并摧毁它们所撞击的任何东西。她为自己的安全感到焦虑,发誓要找到一个安全的地方(一个永远不会被流星…...

RabbitMQ实战:Springboot集成RabbitMQ并验证五种消息模型
这目录 一、添加依赖二、配置文件中添加RabbitMQ访问配置三、消息生产者代码四、消息消费者代码五、验证参考资料 一、添加依赖 <!--AMQP依赖,包含RabbitMQ--><dependency><groupId>org.springframework.boot</groupId><artifactId>s…...
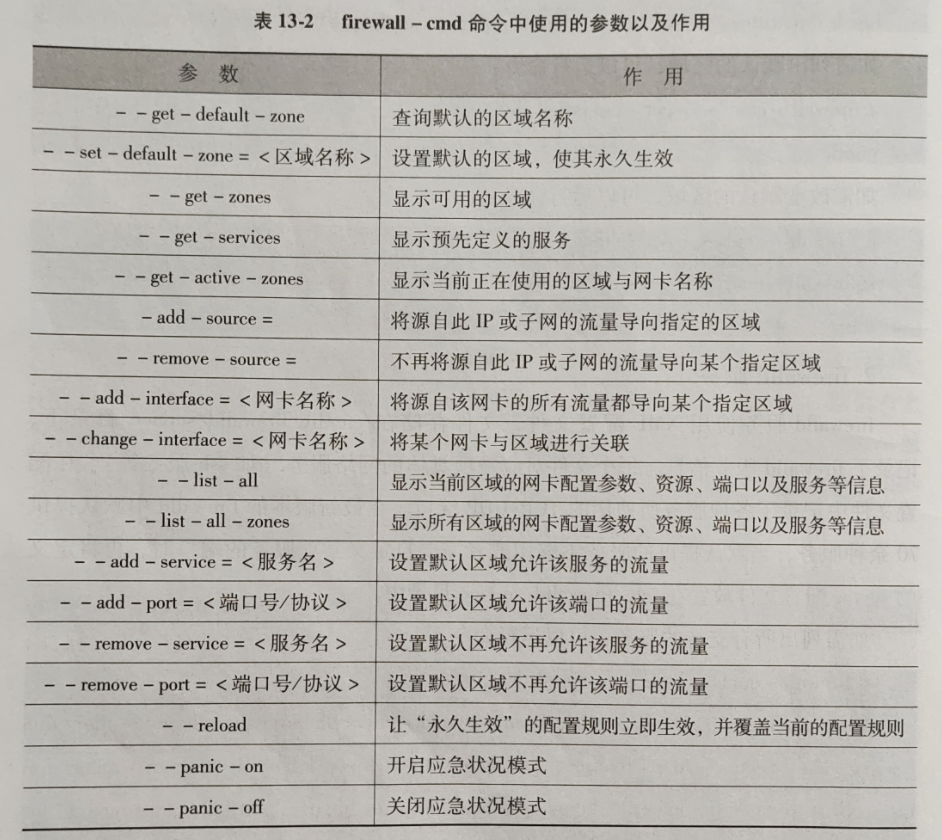
配置与管理防火墙
配置与管理防火墙 1,概念:设置在不同网络或网络安全域之间的一系列部件的组合。 2,功能:保护内网中易手攻击的服务;控制内外网之间网络系统的访问;隐藏内网的IP地址及结构的细节,提高网络保护…...
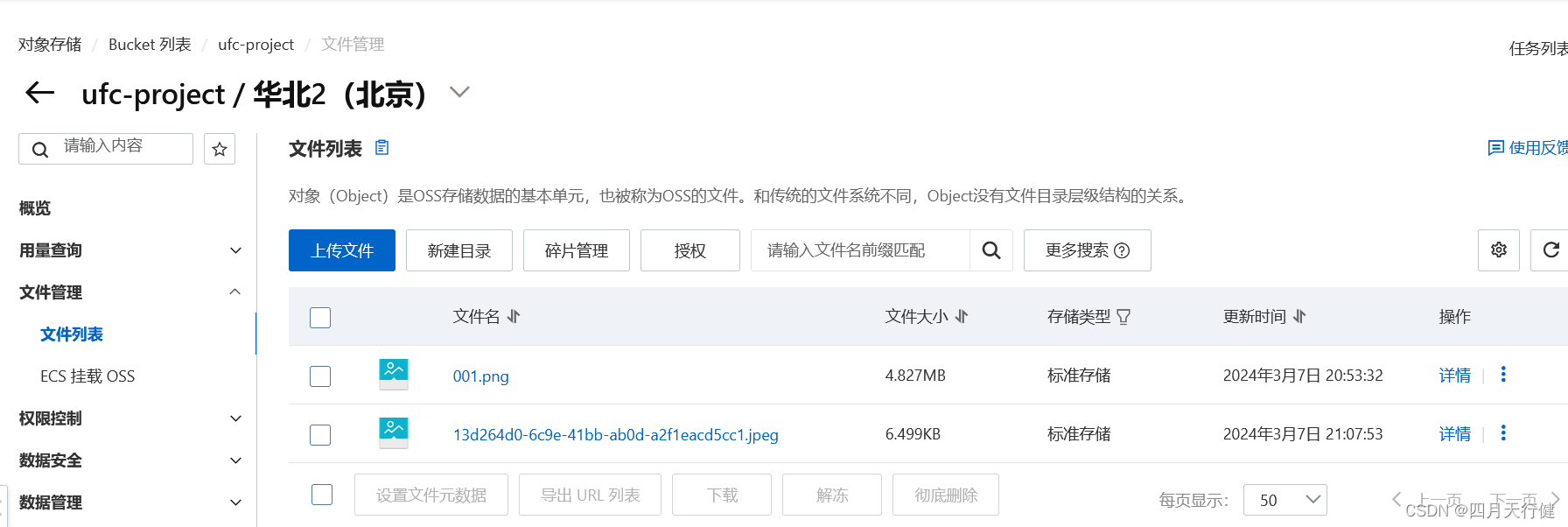
【SpringBoot】-- 实现本地文件/图片上传到服务器生成url地址
在java项目中你可能会有以下需求:用户上传本地图片,然后展示在网页上。本篇文章将使用阿里云oss实现上传图片到oss,oss生成url。 一、准备工作 首先进入阿里云,按如下操作 进入创建页面,修改读写权限为公共读 然后进…...
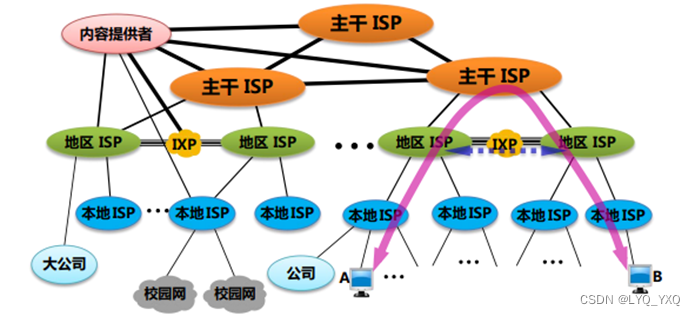
计算机基础专升本笔记十四-计算机网络基础(一)
计算机基础专升本笔记十四-计算机网络基础(一) 一、计算机网络的发展历程 第一代计算机网络(数据通信) 以数据通信为主的第一代计算机网络。主要是指美国军方用于防控系统的一种联机系统。它只是计算机网络的雏形。 第二代计算…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...
