代码随想录算法训练营第三十八天|动态规划|理论基础、509. 斐波那契数、70. 爬楼梯、746. 使用最小花费爬楼梯
理论基础
文章
说实话,没做过题连理论基础都看不懂
1 确定dp数组(dp table)以及下标的含义
2 确定递推公式
3 dp数组如何初始化
4 确定遍历顺序
5 举例推导dp数组
这道题目我举例推导状态转移公式了么?
我打印dp数组的日志了么?
打印出来了dp数组和我想的一样么?
509. 斐波那契数
文章
斐波那契数,通常用 F(n) 表示,形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是: F(0) = 0,F(1) = 1 F(n) = F(n - 1) + F(n - 2),其中 n > 1 给你n ,请计算 F(n) 。
示例 1:
输入:2
输出:1
解释:F(2) = F(1) + F(0) = 1 + 0 = 1
示例 2:
输入:3
输出:2
解释:F(3) = F(2) + F(1) = 1 + 1 = 2
示例 3:
输入:4
输出:3
解释:F(4) = F(3) + F(2) = 2 + 1 = 3
提示:
0 <= n <= 30
题目简单,用于理解动态规划
class Solution {
public:int fib(int N) {if (N <= 1) return N;int dp[2];dp[0] = 0;dp[1] = 1;for (int i = 2; i <= N; i++) {int sum = dp[0] + dp[1];dp[0] = dp[1];dp[1] = sum;}return dp[1];}
};
当然可以用递归的方法
70. 爬楼梯
文章
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
注意:给定 n 是一个正整数。
示例 1:
输入: 2
输出: 2
解释: 有两种方法可以爬到楼顶。
1 阶 + 1 阶
2 阶
示例 2:
输入: 3
输出: 3
解释: 有三种方法可以爬到楼顶。
1 阶 + 1 阶 + 1 阶
1 阶 + 2 阶
2 阶 + 1 阶
想不出来啊
到第三层楼梯的状态可以由第二层楼梯 和 到第一层楼梯状态推导出来,那么就可以想到动态规划了。
dp[i]: 爬到第i层楼梯,有dp[i]种方法
class Solution {
public:int climbStairs(int n) {if (n <= 1) return n;int dp[3];dp[1] = 1;dp[2] = 2;for (int i = 3; i <= n; i++) {int sum = dp[1] + dp[2];dp[1] = dp[2];dp[2] = sum;}return dp[2];}
};
746. 使用最小花费爬楼梯
文章讲解
数组的每个下标作为一个阶梯,第 i 个阶梯对应着一个非负数的体力花费值 cost[i](下标从 0 开始)。
每当你爬上一个阶梯你都要花费对应的体力值,一旦支付了相应的体力值,你就可以选择向上爬一个阶梯或者爬两个阶梯。
请你找出达到楼层顶部的最低花费。在开始时,你可以选择从下标为 0 或 1 的元素作为初始阶梯。
示例 1:
输入:cost = [10, 15, 20]
输出:15
解释:最低花费是从 cost[1] 开始,然后走两步即可到阶梯顶,一共花费 15 。
示例 2:
输入:cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1]
输出:6
解释:最低花费方式是从 cost[0] 开始,逐个经过那些 1 ,跳过 cost[3] ,一共花费 6 。
提示:
cost 的长度范围是 [2, 1000]。
cost[i] 将会是一个整型数据,范围为 [0, 999]
能想到由前两步推,但是没太象具体,不打算走非min的步了,其实不对。
还是要按照步骤来
min(dp1 + cost[i - 1], dp0 + cost[i - 2])
class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {int dp0 = 0;int dp1 = 0;for (int i = 2; i <= cost.size(); i++) {int dpi = min(dp1 + cost[i - 1], dp0 + cost[i - 2]);dp0 = dp1; // 记录一下前两位dp1 = dpi;}return dp1;}
};相关文章:

代码随想录算法训练营第三十八天|动态规划|理论基础、509. 斐波那契数、70. 爬楼梯、746. 使用最小花费爬楼梯
理论基础 文章 说实话,没做过题连理论基础都看不懂 1 确定dp数组(dp table)以及下标的含义 2 确定递推公式 3 dp数组如何初始化 4 确定遍历顺序 5 举例推导dp数组 这道题目我举例推导状态转移公式了么? 我打印dp数组的日志了么&…...

运维知识点-JBoss
JBoss 介绍介绍 JBoss是一个基于J2EE的开放源代码的应用服务器,也是一个运行EJB(Enterprise JavaBean)的容器和服务器。它支持EJB 1.1、EJB 2.0和EJB3的规范,体现了J2EE规范中最新的技术。JBoss遵循LGPL许可,可以在任何商业应用中免费使用,并且由开源社区开发,这使得JB…...
HarmonyOS—配置编译构建信息
在进行应用/服务的编译构建前,需要对工程和编译构建的Module进行设置。API Version 9、API Version 8与API Version 4~7的构建体系不同,因此在设置编译构建信息时也存在差异: API Version 9:需要对构建配置文件、构建脚本、应用依…...
Chrome浏览器好用的几个扩展程序
Chrome好用的扩展程序 背景目的介绍JsonHandle例子未完待续。。。。。。 背景 偶然在往上看到Chrome有很多好用的扩展程序,比较好用,因此记录下比较实用的扩展程序。 目的 记录Chrome浏览器好用的插件。 介绍 JsonHandle下载以及无法扩展插件的解决…...
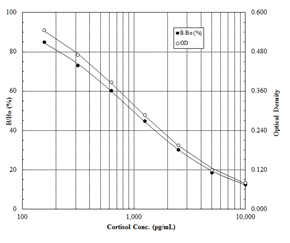
Enzo Life Sciences Cortisol(皮质醇) ELISA kit
皮质醇又称为氢化可的松,是一种由胆固醇合成的类固醇激素。它是肾上腺皮质产生和分泌的主要糖皮质激素。皮质醇在血液中以游离皮质醇的形式存在,或与皮质类固醇结合球蛋白(CBG)结合。皮质醇水平在早上7点左右最高,晚上最低。皮质醇可以调节新…...
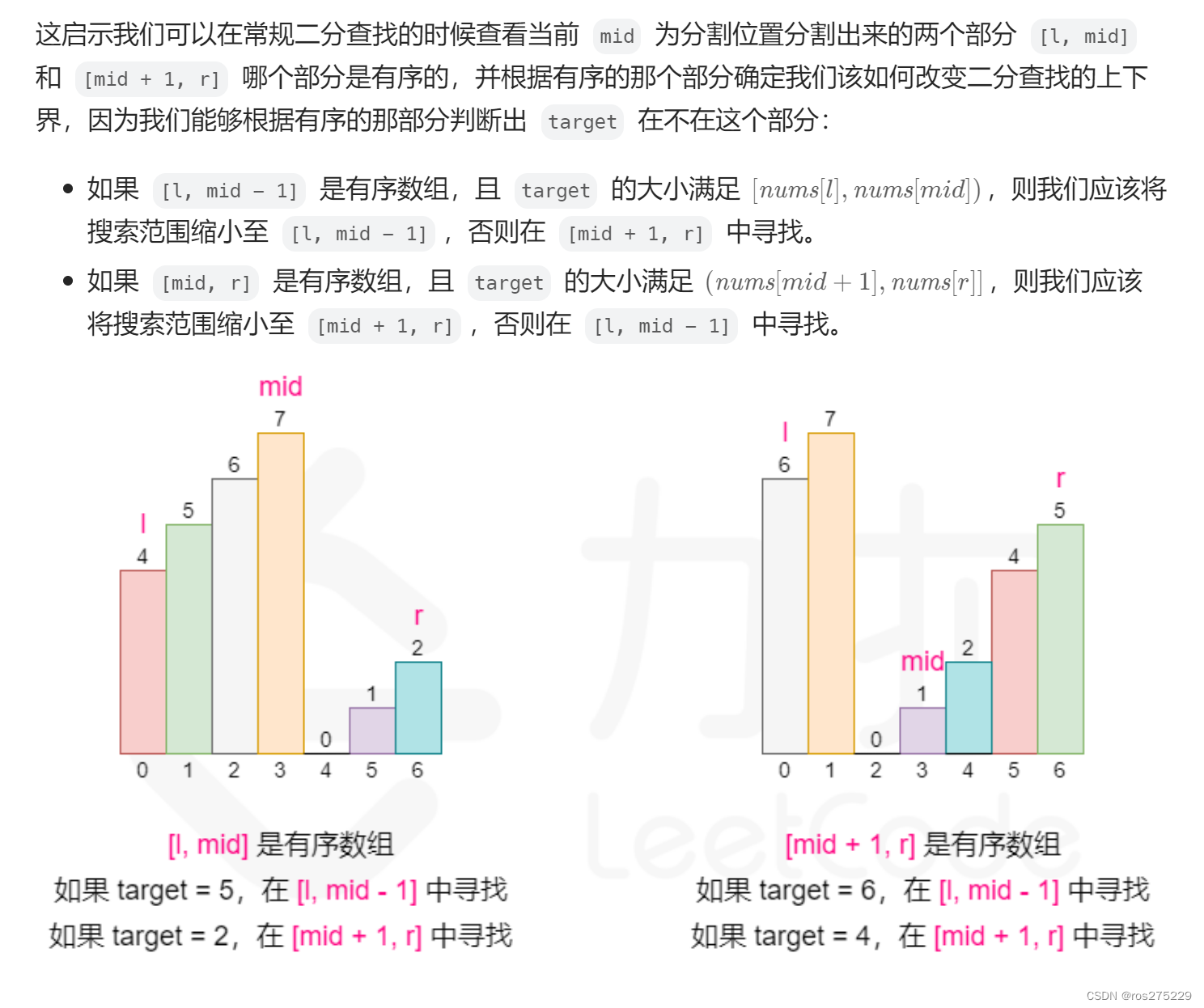
面试经典150题 -- 二分查找 (总结)
总的链接 : 面试经典 150 题 - 学习计划 - 力扣(LeetCode)全球极客挚爱的技术成长平台 二分算法模板 : 详见 : 基础二分学习笔记-CSDN博客 35 . 搜索插入位置 链接 : . - 力扣(LeetCode) 思路 : 用二分查找第一个>t…...

蓝牙耳机怎么选择比较好?2024年热门机型推荐大揭秘!
蓝牙耳机已经成为了我们日常生活中不可或缺的一部分,随着技术的发展,人们对蓝牙耳机的要求也在不断提升,不仅希望音质出色,还希望能够在不同的场景下使用。然而,如何挑选一款适合自己的蓝牙耳机却是一门学问。今天&a…...

强制Unity崩溃的两个方法
在Unity中,这两种方法都可以用于强制使应用程序崩溃,但它们的作用略有不同: Application.ForceCrash(0); 这个方法会强制应用程序崩溃,并且参数传入的是一个整数值。当参数为0时,它会导致应用程序崩溃并显示一个“Acce…...

中间件 | Redis - [big-key hot-key]
INDEX 1 big-keyhot-key 1 big-key 分类 字符串型 big-key:字符串最大可以到 512M集合型 big-key:集合个数可以到 2^23 问题 内存空间不均匀指令耗时增加:redis 是单线程的,部分操作的时间复杂度是 O(n) 的,big-ke…...

STM32基础--自己构建库函数
什么是 STM32 函数库 固件库是指“STM32 标准函数库”,它是由 ST 公司针对 STM32 提供的函数接口,即API (Application Program Interface),开发者可调用这些函数接口来配置 STM32 的寄存器,使开发人员得以脱离最底层的寄存器操作…...

网站被插入虚假恶意链接怎么办?
在当前的电信和网络环境中,诈骗案件频发,许多受害者不幸上当,主要原因是他们点击了诈骗者发送的假链接。这些诈骗网站经常模仿真实网站的外观,使人难以分辨真伪。那么,我们应如何鉴别这些诈骗链接呢? 下面…...
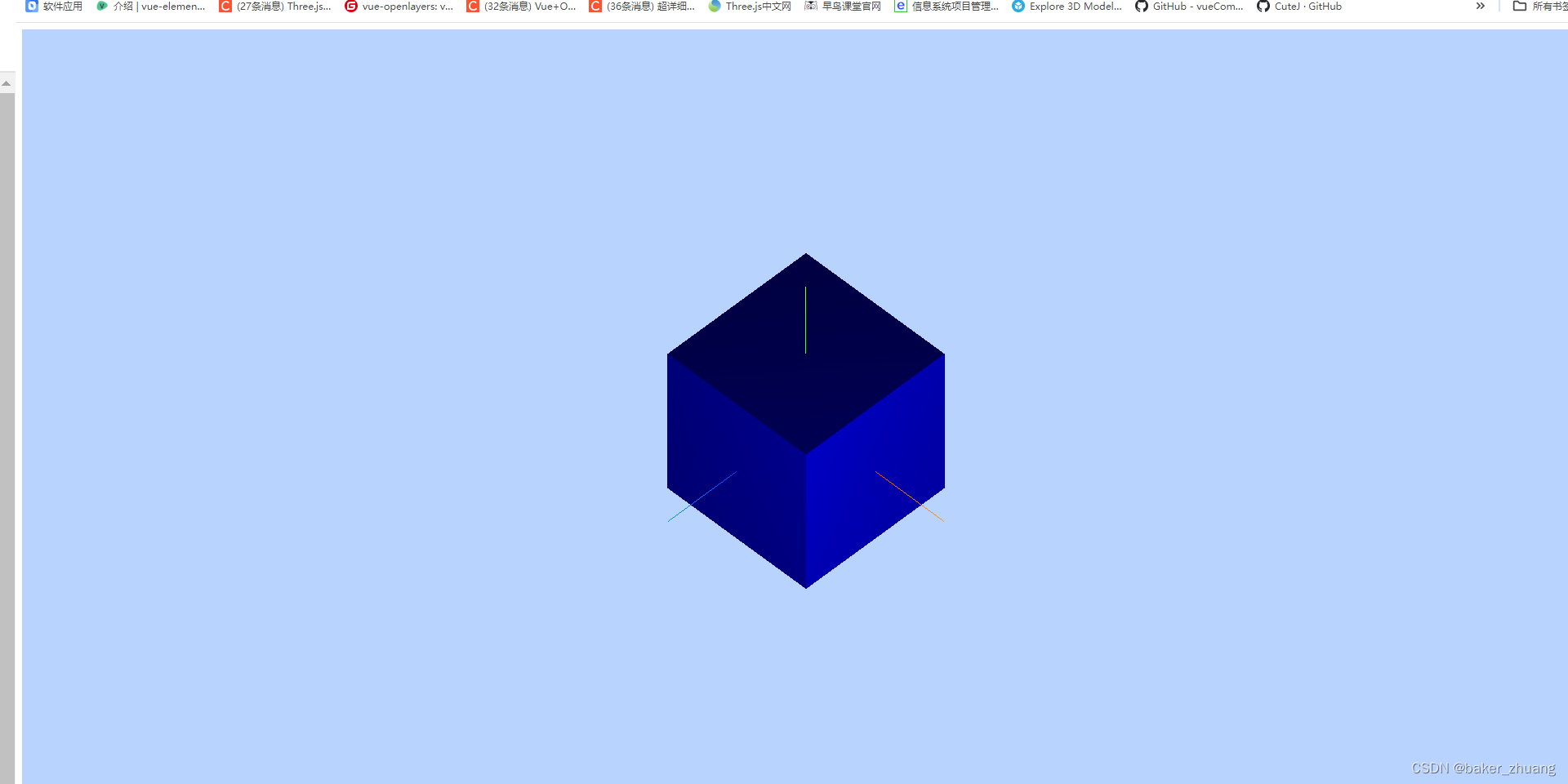
ThreeJs限制模型拖动的范围
之前有讲过ThreeJs中对模型的拖动功能,使用DragControl组件,将模型放到组件的集合中,就可以拖动点击的模型了,这节细化下怎么控制拖动,比如之拖动z轴,或者限制拖动x轴的范围在某个区间: 首先还是…...

关于JVM的小总结(待补充)
JVM组成及他们之间的关系 装载类子系统字节码执行引擎运行时数据区 装载类子系统 类加载器字节码调节器类加载运行时数据区 字节码执行引擎 运行时数据区 线程私有 虚拟机栈本地方法栈程序计数器 线程共享 堆方法区(元空间)...
day37 贪心算法part6
738. 单调递增的数字 中等 提示 当且仅当每个相邻位数上的数字 x 和 y 满足 x < y 时,我们称这个整数是单调递增的。 给定一个整数 n ,返回 小于或等于 n 的最大数字,且数字呈 单调递增 。 不知道怎么讲思路……以9287举例,…...

38女神节:剧情热梗小游戏新品!预售1折秒杀,手慢无
抖音热剧情热梗小游戏《逆袭大冒险》登录 Cocos Store 预售开启!游戏包含 20剧情 40 关卡,先来看下视频吧! 游戏内嵌多种小游戏玩法,是不是很有亲切感呢?抽针、流体、重力 3.8女神节特价预售 欢迎加入迷萌游戏《逆袭大…...

岩土工程监测仪器振弦采集仪的发展历程与国内外研究现状
岩土工程监测仪器振弦采集仪的发展历程与国内外研究现状 岩土工程监测仪器河北稳控科技振弦采集仪是用于测量土体或岩石地层的力学性质、地层结构、地下水位等参数的一种仪器设备。它通过振动在地下传播的声波信号的传播速度和特性,来推断地层的物理性质。以下是对…...

Git 掌握
目录 一、前言 二、centos安装Git 三、Git基本操作 (1) 创建Git本地仓库 (2) 配置Git (3) 认识工作区,暂存区,版本库 四、添加文件 五、查看.git文件 六、修改文件 七、版本回退 八、撤销修改 (1) 场景一 对于还没有add的代码 (2) 场景二 已…...
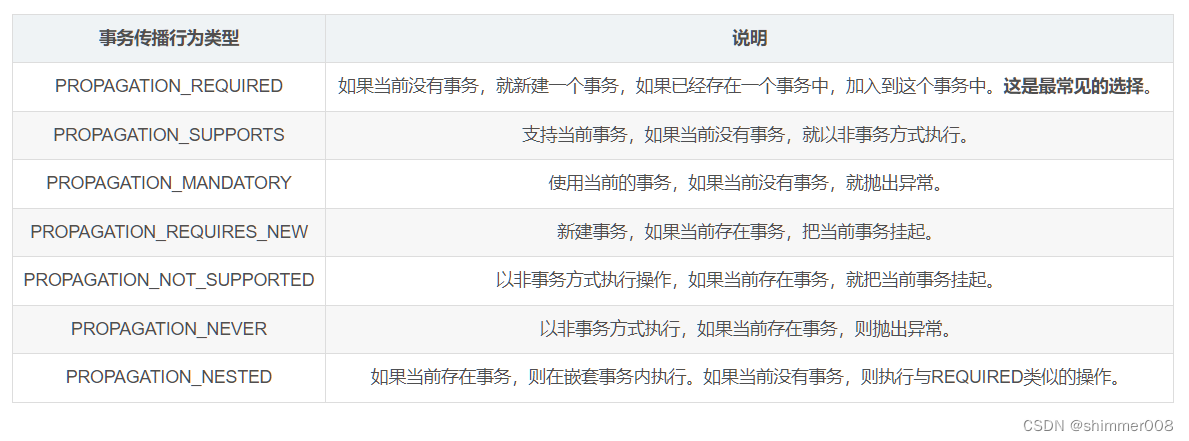
面试题之——事务失效的八大情况
事务失效的八大情况 一、非public修饰的方法 Transactional注解只能在在public修饰的方法下使用。 /*** 私有方法上的注解,不生效(因私有方法Spring扫描不到该方法,所以无法生成代理)*/ Transactional private boolean test() …...
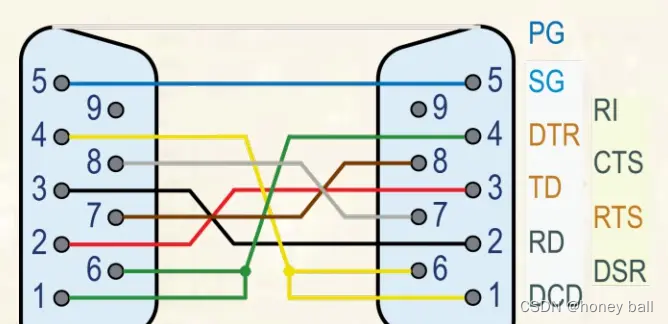
一些硬件知识(六)
防反接设计: 同步电路和异步电路的区别: 同步电路:存储电路中所有触发器的时钟输入端都接同一个时钟脉冲源,因而所有触发器的状态的变化都与所加的时钟脉冲信号同步。 异步电路:电路没有统一的时钟,有些触发器的时钟输入端与时钟脉冲源相连…...

前端React篇之哪些方法会触发 React 重新渲染?重新渲染 render 会做些什么?
目录 哪些方法会触发 React 重新渲染?重新渲染 render 会做些什么?setState()案例需求总结 forceUpdate()案例需求总结 props改变案例需求总结 context改变案例需求总结 哪些方法会触发 React 重新渲染?重新渲染 render 会做些什么࿱…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...
