利用“定时执行专家”循环执行BAT、VBS、Python脚本——含参数指定功能
目录
一、软件概述
二、VBS脚本执行设置
三、触发器设置
四、功能亮点
五、总结
在自动化办公和日常计算机任务管理中,定时执行脚本是一项非常重要的功能。今天,我将为大家带来一款名为“定时执行专家”的软件的评测,特别是其定时执行VBS脚本并具备指定脚本参数的功能。
一、软件概述
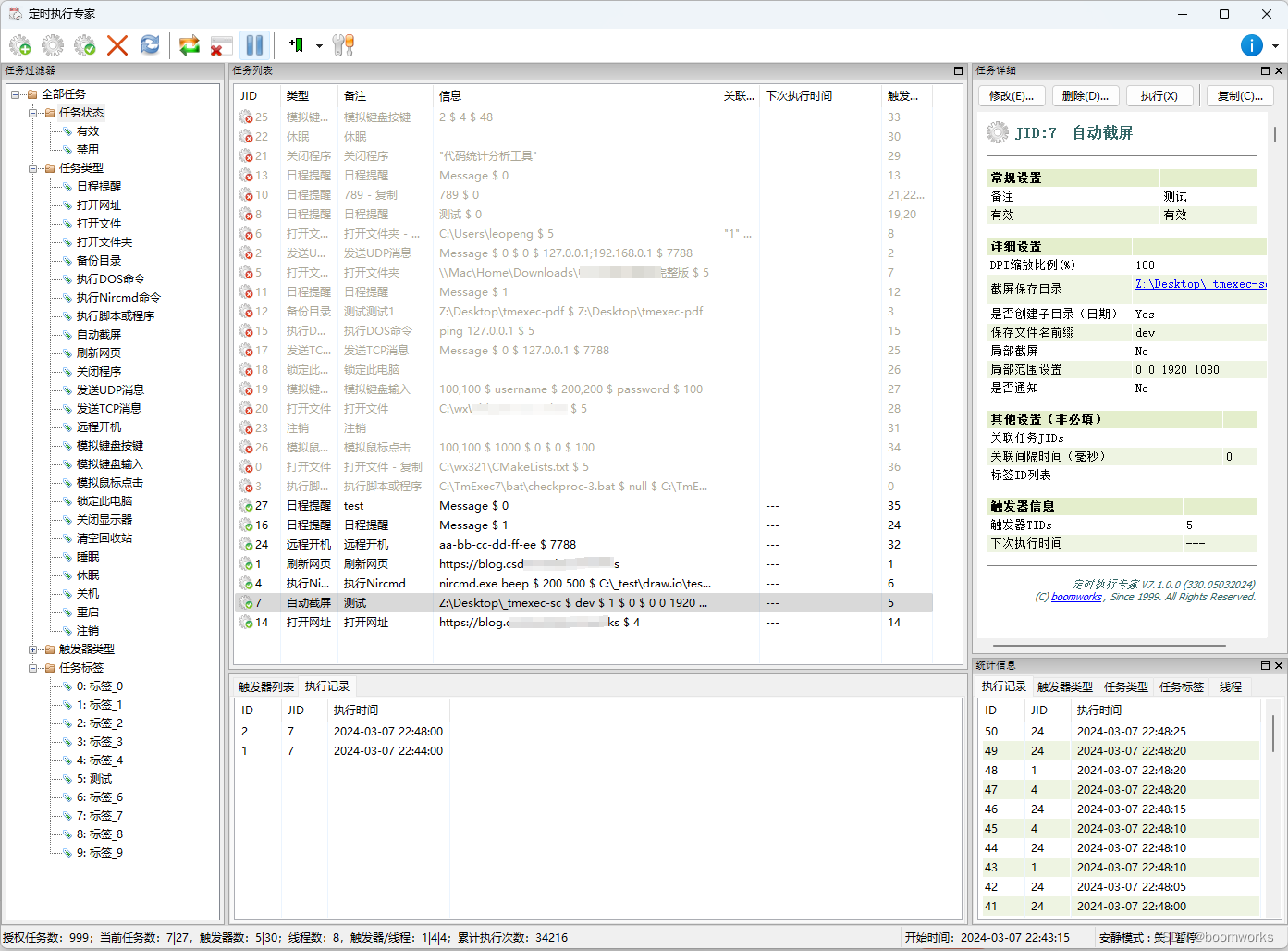
《定时执行专家》是一款制作精良、功能强大、毫秒精度、专业级的定时任务执行软件。软件具有 25 种【任务类型】、12 种【触发器】触发方式,并且全面支持界面化【Cron表达式】设置。软件采用多线程并发方式检测任务触发和任务执行,能够达到毫秒级的执行精度,可以同时支持200个以上任务的毫秒级触发。该软件界面简洁直观,操作便捷,是办公自动化的得力助手。
二、VBS脚本执行设置
首先,我们打开“定时执行专家”软件,并在任务对话框中选择“执行脚本或程序”作为任务类型。接着,我们需要设置VBS脚本的路径、参数和工作目录等信息。

在“程序或脚本”字段中,我们输入VBS脚本的完整路径,确保软件能够准确找到并执行该脚本。在“参数”字段中,我们可以指定VBS脚本所需的参数,这对于需要传递不同参数来执行不同任务的脚本来说非常有用。最后,在“工作目录”字段中,我们设置脚本所在的工作目录,以便脚本能够正确访问相关文件。
三、触发器设置
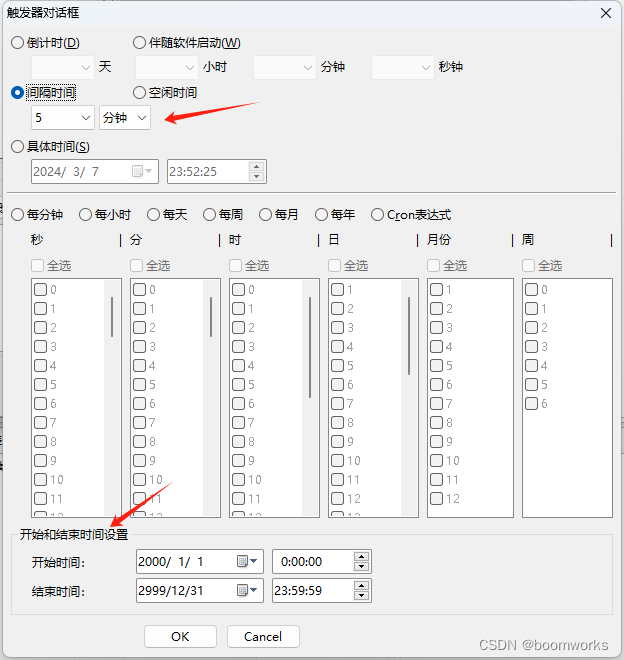
设置好VBS脚本的执行信息后,我们需要在任务对话框中点击“新建触发器”按钮,打开触发器对话框。在这里,我们选择“间隔时间”作为触发方式,并设置间隔时间为5分钟。这样,软件就会每隔5分钟自动执行一次我们设置的VBS脚本。
值得一提的是,“定时执行专家”软件支持多种时间单位,包括时、分、秒,这使得我们可以根据实际需求灵活设置触发间隔。
四、功能亮点
- 参数指定功能强大:通过指定VBS脚本的参数,我们可以实现脚本的多样化执行,满足不同的自动化需求。
- 定时执行精准可靠:软件采用高精度定时器,确保任务能够按照设定的时间间隔准确执行。
- 界面简洁易用:软件界面设计简洁明了,操作流程清晰易懂,即使对于非专业人士来说也能轻松上手。
五、总结
我们可以看出“定时执行专家”软件在定时执行VBS脚本方面表现出色,特别是其参数指定功能使得脚本执行更加灵活多变。同时,软件的定时执行功能精准可靠,能够满足各种自动化办公需求。如果你正在寻找一款能够高效执行VBS脚本的定时任务管理软件,那么“定时执行专家”绝对是一个值得考虑的选择。
相关文章:

利用“定时执行专家”循环执行BAT、VBS、Python脚本——含参数指定功能
目录 一、软件概述 二、VBS脚本执行设置 三、触发器设置 四、功能亮点 五、总结 在自动化办公和日常计算机任务管理中,定时执行脚本是一项非常重要的功能。今天,我将为大家带来一款名为“定时执行专家”的软件的评测,特别是其定时执行VB…...

【算法集训】基础算法:模拟
一、基本理解 顾名思义,就是题目要求做什么,代码中就跟着做就可以。 二、题目练习 1252. 奇数值单元格的数目 根据题目要求列出如下代码。需要注意填充列和行的时候注意下标。 int oddCells(int m, int n, int** indices, int indicesSize, int* in…...
基于SSM的房客源信息管理系统设计与实现
目 录 摘 要 I Abstract II 引 言 1 1 相关技术 3 1.1 SSM框架 3 1.2 Vue框架 3 1.3 ECharts 3 1.4 JQuery技术 3 1.5 本章小结 4 2系统分析 5 2.1 需求分析 5 2.2 非功能需求 8 2.3 本章小节 8 3 系统设计 9 3.1 系统总体设计 9 3.1.1 系统体系结构 9 3.1.2 系统目录结构 9 3…...

常见数据类型
目录 数据类型 字符串 char nchar varchar varchar2 nvarchar 数字 number integer binary_float binary_double float 日期 date timestamp 大文本数据 大对象数据 Oracle从入门到总裁:https://blog.csdn.net/weixin_67859959/article/details/135209645 数…...
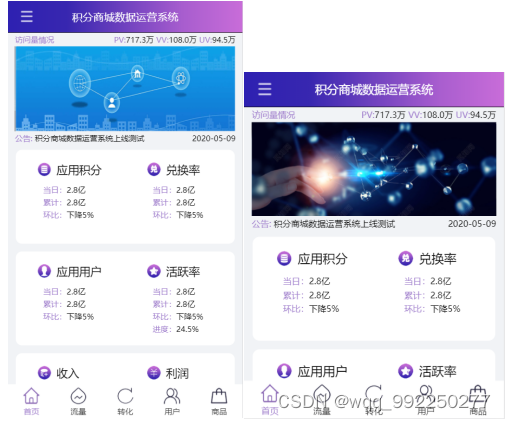
基于vue的联通积分商城数据可视化APP设计与实现
目 录 摘 要 I Abstract II 引 言 1 1 前端技术介绍 3 1.1 前端开发语言 3 1.1.1 HTML5 3 1.1.2 CSS3 3 1.1.3 JavaScript 3 1.2 MVVM开发模式 4 1.3 Vue框架 4 1.4 Axios技术 5 1.5 ECharts 5 1.6 数据库技术 5 1.7 本章小结 6 2 前端开发的分析 7 2.1 功能性需求分析 7 2.2 …...
)
2024年flink面试真题(一)
(北京)taskManager和slot、task的关系 ? (北京)flink状态太大怎么解决 ? (北京 flink提交方式和运行模式 ? (北京) 怎么提交的实时任务,有多少Job Manager? &…...

Java面试挂在线程创建后续,不要再被八股文误导了!创建线程的方式只有1种
线程创建之源 OK!咱们闲话少叙,直接进入正题,回顾一下通过实现Runnable接口,重写run方法创建线程的方式,真的可以创建一个线程吗?来看下面这段demo。 【代码示例1】 public class Test implements Runnab…...

JavaEE面试题
一、String面试题 1、String s1 "123"; 和 String s2 new String("123");的区别 在Java中,"String s1 "123";"和"String s2 new String("123");"这两行代码有一些重要的区别: "…...

探索macOS上的最佳MySQL客户端工具
在数据库管理和开发的世界里,选择一个高效、功能全面的客户端工具对于提升工作效率至关重要。尤其对于使用 macOS 的开发者来说,一个好的 MySQL 客户端不仅可以简化数据库操作,还能提供强大的数据分析和管理功能。本文将介绍几款适用于 macOS…...

[Android] MediaPlayer SDK API glance
参考: https://developer.android.com/reference/android/media/MediaPlayer 如何使用MediaPlayer SDK: https://developer.android.com/media/platform/mediaplayer 概述: 音视频的 playback。创建 MediaPlayer 的线程必须和调用 SDK 接口…...
原始手写helloworld并打jar包允许
1.创建文件夹test统一在其中操作 2.创建hello.java文件 【hello.txt改属性为hello.java】并在里面添加代码 public class hello {public static void main(String[] args) {System.out.println("hello world");} } 注意:类名与文件名一致 然后运行…...
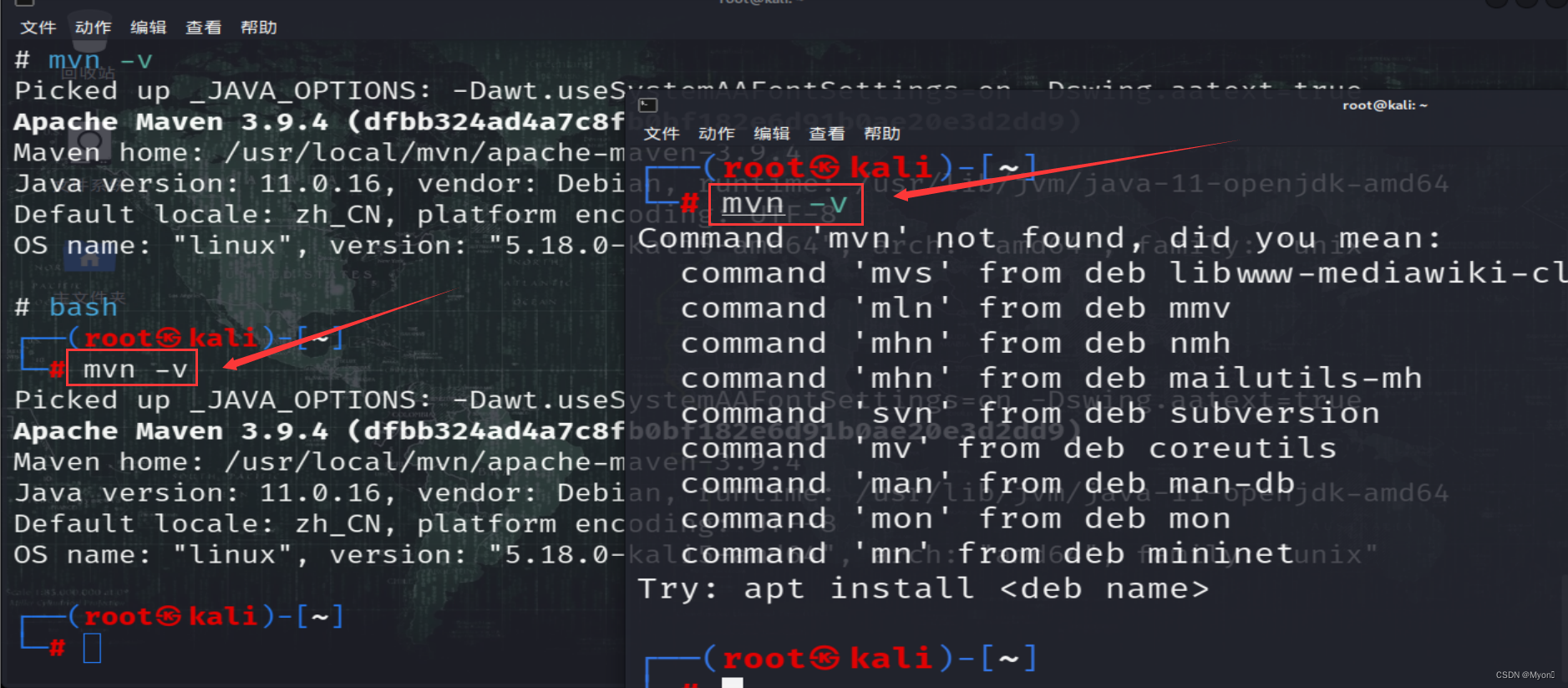
maven 的安装与配置(Command ‘mvn‘ not found)修改配置文件后新终端依旧无法识别到 mvn 命令
下载 maven 安装包 wget https://dlcdn.apache.org/maven/maven-3/3.9.4/binaries/apache-maven-3.9.4-bin.tar.gz 解压 apache-maven-3.9.4-bin.tar.gz tar -zxvf apache-maven-3.9.4-bin.tar.gz 找到文件解压到的位置,由于解压时我们没有指定路径,因…...
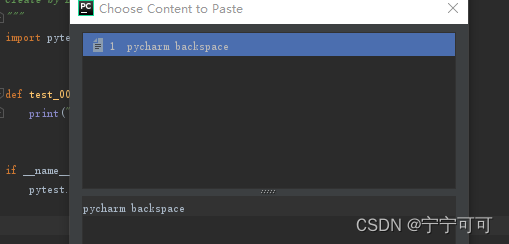
Pycharm无法粘贴外部文本问题
Pycharm无法粘贴外部文本问题 百度找了好多是因为安装了vim,最后发现是因为pycharm粘贴框存在了很多内容导致 操作方法: 1、清理所有缓存的复制内容 ctrlshiftV 可以看到编译器所有缓存下来的复制文本 2、ctrlA然后delete 解决:此时再复…...
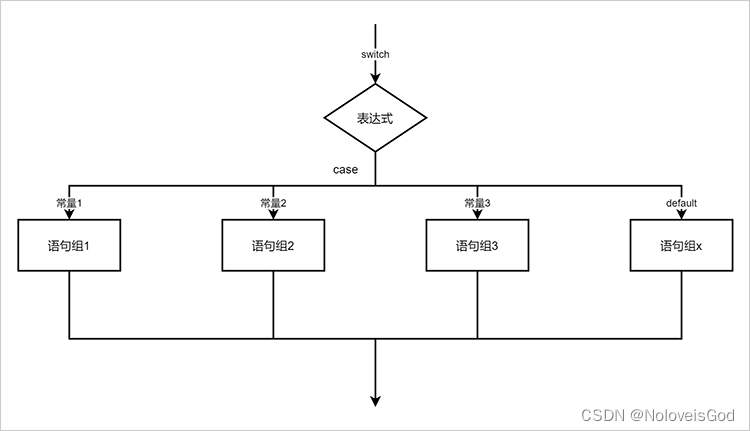
学习Java的第四天
目录 一、if选择结构 1、基本if选择结构 语法结构: 流程图: 示例: 2、if-else 选择结构 语法结构: 流程图: 示例: 3、多重if选择结构 语法结构: 流程图: 示例:…...

【Javaweb】【瑞吉外卖】登录功能plus--拦截器filterinterceptors实现
上手第二天,做到登录拦截器部分 需求:完成目标是,只有在登录的情况下才想让其访问后端,没有登录禁止访问,并且让其跳转。 这里有一个比较好的思想是:后端程序要主要需要考虑的是拦截接口,不能让…...
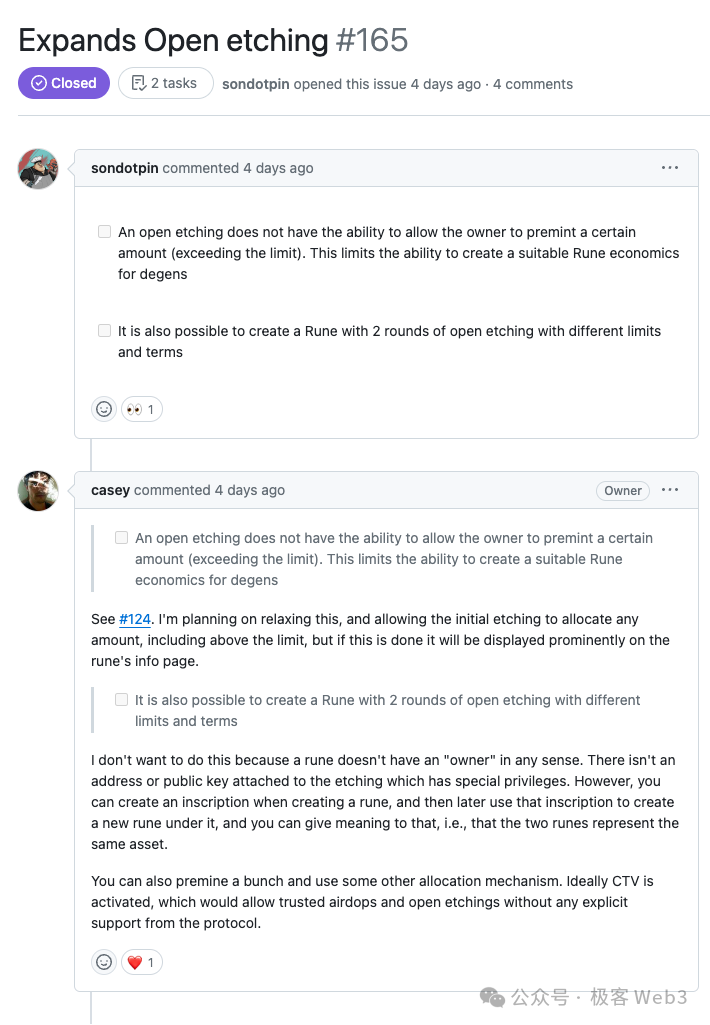
关于 Runes 协议及「公开铭刻」发行机制的拓展讨论
撰文:MiX 编辑:Faust,极客 web3 2024 年 3 月 2 日,Runes 生态基础设施项目 Rune alpha 的创始人,在 Github 的公开议题中,与 Runes 协议创始人 Casey 展开了讨论,双方对如何拓展 Runes 协议的…...
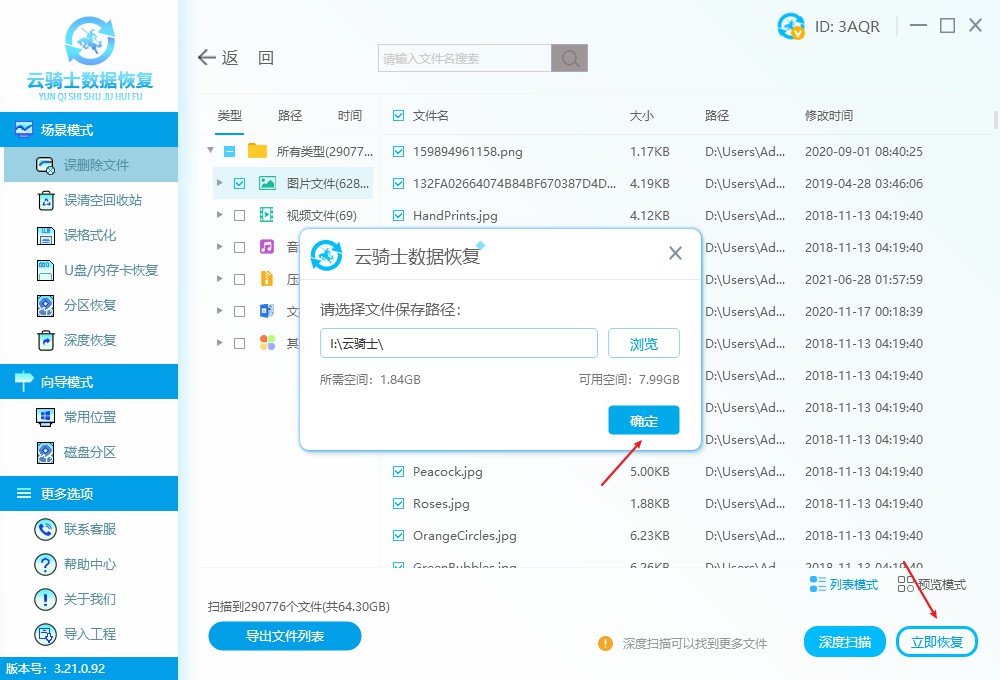
chkdsk修复会造成文件丢失吗?chkdsk数据丢失还能恢复吗
在Windows操作系统中,CHKDSK是一个强大的磁盘检查工具,它可以帮助我们诊断并修复硬盘的各种错误。然而,许多用户在运行CHKDSK之前都会担心一个问题:CHKDSK修复会造成文件丢失吗?如果不幸发生了数据丢失,CHK…...

Hypermesh2019快捷键大全
1、F系列 F* | ShiftF* F1 | 打开帮助文件 | color F2 | delete | temp nodes F3 | replace | edges F4 | distance | tran…...
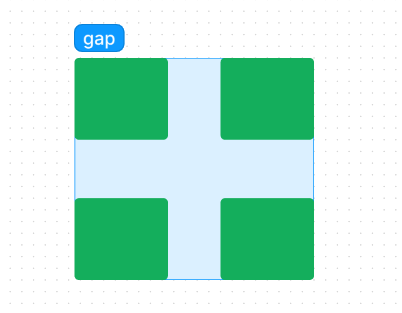
CSS布局——Flexbox基础使用
基础概念 Flexbox布局的概念 Flexbox布局是一种布局的模式,用来在一个维度上为项目设置布局 容器 在HTML中大多数元素例如div、ul、main块元素,span、em、i行内元素都可以作为Flex容器,它的作用是开启一个Flex布局模式,你只需…...
:容器化应用的航空母舰)
Kubernetes(K8s):容器化应用的航空母舰
一、Kubernetes简介 Kubernetes(K8s)是一个开源的容器编排系统,它的出现就像是为容器化应用提供了一艘强大的航空母舰。在这艘母舰上,你的应用容器就像是一架架战斗机,Kubernetes负责指挥它们起飞、飞行、降落&#x…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...

Linux部署私有文件管理系统MinIO
最近需要用到一个文件管理服务,但是又不想花钱,所以就想着自己搭建一个,刚好我们用的一个开源框架已经集成了MinIO,所以就选了这个 我这边对文件服务性能要求不是太高,单机版就可以 安装非常简单,几个命令就…...
