day38 动态规划part1
509. 斐波那契数
简单
斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是:
F(0) = 0,F(1) = 1
F(n) = F(n - 1) + F(n - 2),其中 n > 1
给定 n ,请计算 F(n) 。
class Solution {public int fib(int n) {if (n < 2) return n;int dpa = 0;int dpb = 1;int dpc = 0;for (int i = 2; i <= n; i++) {dpc = dpa + dpb;dpa = dpb;dpb = dpc;}return dpc;}
}
70. 爬楼梯
简单
提示
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
没做过的话觉得好难,其实是有规律的,因为每次只能跳一或者两个台阶,所以,要想跳到f(n),就必须跳到f(n - 1) 或者 f(n - 2),所以f(n) = f(n - 1) + f(n - 2) , 有人可能会讲,f(n - 1) 和 f(n - 2) 里有没有重合的跳法,因为f(n - 1) 必然经过 f(n - 2), 这就有点问题了,因为f(x) 表示爬到第 x 级台阶的方案数,题目让你求得是方案数,不是爬楼梯的步数。f(n) = f(n - 1) + f(n - 2) 不能再加2哈,因为你到了f(n - 1)只有这种方案能上楼,f(n - 2)同理,记住,是方案的数量,不是上楼的步数。不要去管f(n - 1) 和f(n - 2),有联系,是有联系,可以没让你去管啊,要管的事f(n) 的算法。说再多没用,自己模拟前4个台阶怎么算的就明白了。

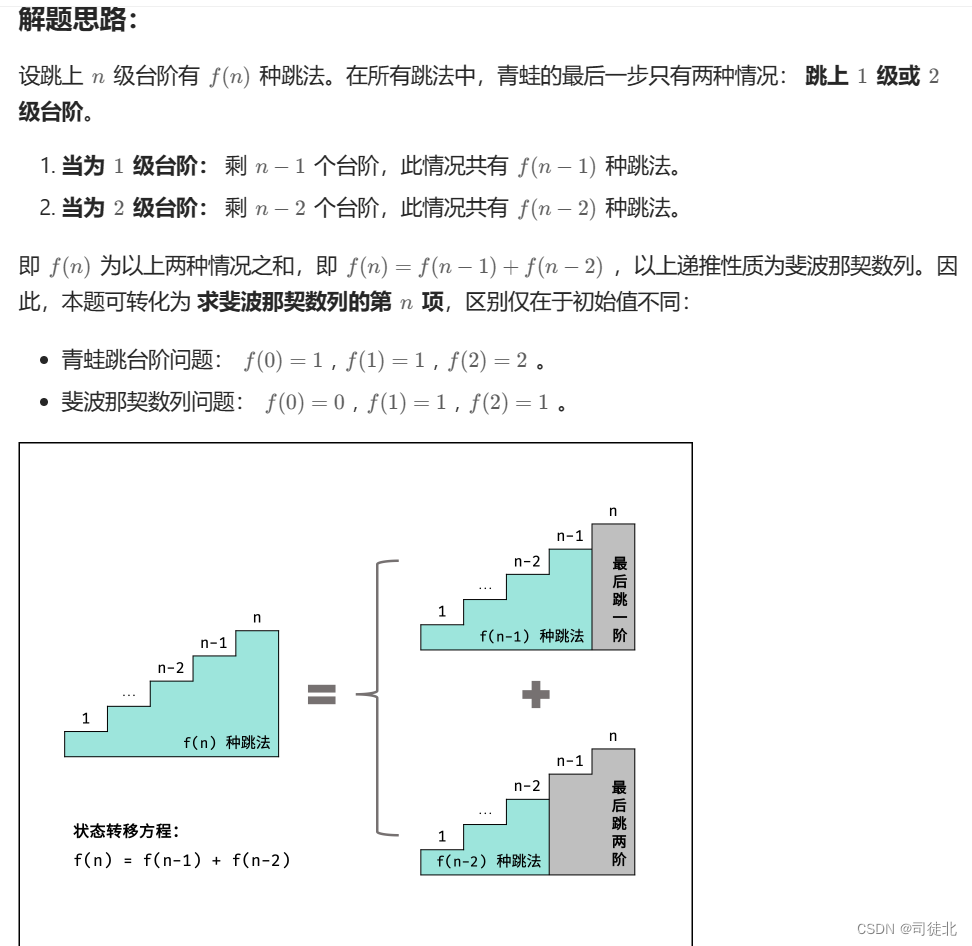
class Solution {public int climbStairs(int n) {if (n < 3) return n;int step1 = 1;int step2 = 2;int step3 = 0;for (int i = 3; i <= n; i++) {step3 = step1 + step2;step1 = step2;step2 = step3;}return step3;}
}
746. 使用最小花费爬楼梯
简单
提示
给你一个整数数组 cost ,其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用,即可选择向上爬一个或者两个台阶。
你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。
请你计算并返回达到楼梯顶部的最低花费
// 这个题也可以不用dp数组,就三个变量就行
class Solution {public int minCostClimbingStairs(int[] cost) {// dp[i]的定义:到达第i台阶所花费的最少体力为dp[i]int[] dp = new int[cost.length + 1]; // 把顶层也算上,多分配一个空间dp[0] = dp[1] = 0; // 可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯,说明代价是0for (int i = 2; i <= cost.length; i++) {// 要么是从下面一个台阶跳上来的,要么是从下面两个台阶跳上来的,选代价最小的就行dp[i] = Math.min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i- 2]);}return dp[cost.length];}
}
用这个题来捋捋思路:
1.确定dp数组以及下标的含义
使用动态规划,就要有一个数组来记录状态,本题只需要一个一维数组dp[i]就可以了。
dp[i]的定义:到达第i台阶所花费的最少体力为dp[i]。
对于dp数组的定义,大家一定要清晰!
2.确定递推公式
可以有两个途径得到dp[i],一个是dp[i-1] 一个是dp[i-2]。
dp[i - 1] 跳到 dp[i] 需要花费 dp[i - 1] + cost[i - 1]。
dp[i - 2] 跳到 dp[i] 需要花费 dp[i - 2] + cost[i - 2]。
那么究竟是选从dp[i - 1]跳还是从dp[i - 2]跳呢?
一定是选最小的,所以dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
3.dp数组如何初始化
看一下递归公式,dp[i]由dp[i - 1],dp[i - 2]推出,既然初始化所有的dp[i]是不可能的,那么只初始化dp[0]和dp[1]就够了,其他的最终都是dp[0]dp[1]推出。
那么 dp[0] 应该是多少呢? 根据dp数组的定义,到达第0台阶所花费的最小体力为dp[0],那么有同学可能想,那dp[0] 应该是 cost[0],例如 cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1] 的话,dp[0] 就是 cost[0] 应该是1。
这里就要说明本题力扣为什么改题意,而且修改题意之后 就清晰很多的原因了。
新题目描述中明确说了 “你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。” 也就是说 到达 第 0 个台阶是不花费的,但从 第0 个台阶 往上跳的话,需要花费 cost[0]。
所以初始化 dp[0] = 0,dp[1] = 0;
4.确定遍历顺序
最后一步,递归公式有了,初始化有了,如何遍历呢?
本题的遍历顺序其实比较简单,简单到很多同学都忽略了思考这一步直接就把代码写出来了。
因为是模拟台阶,而且dp[i]由dp[i-1]dp[i-2]推出,所以是从前到后遍历cost数组就可以了。
但是稍稍有点难度的动态规划,其遍历顺序并不容易确定下来。 例如:01背包,都知道两个for循环,一个for遍历物品嵌套一个for遍历背包容量,那么为什么不是一个for遍历背包容量嵌套一个for遍历物品呢? 以及在使用一维dp数组的时候遍历背包容量为什么要倒序呢?
这些都与遍历顺序息息相关。当然背包问题后续「代码随想录」都会重点讲解的!
5.举例推导dp数组
相关文章:

day38 动态规划part1
509. 斐波那契数 简单 斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是: F(0) 0,F(1) 1 F(n) F(n - 1) F(n - 2),…...
01背包问题 刷题笔记
思路 dp 用f[i][j]来表示当体积为j时 考虑前i件物品可以获得的 最大值 记住f[i][j]本身是个价“价值” 考虑两种状态 是否将第i件物品放入背包里面 将背包的体积从小到大递增来进行考虑 首先 考虑条件 如果当前增加的体积放不下下一件物品 则该体积 可以获得的最大值可以直接…...
)
docker安装包(Linux和windows)
Linux——docker-20.10.9.tgz 网盘地址:链接:https://pan.baidu.com/s/1T3qfVZ-uT-vMAo8w6heTMw 提取码:qu85 windows——docker19.03.1 链接:https://pan.baidu.com/s/1mK6hqhkGCBs6tdBHJxrdPw 提取码:4dkj...
RabbitMQ 安装使用
文章目录 RabbitMQ 安装使用安装下载 Erlang下载 RabbitMQ 的服务安装好后看是否有 RabbitMQ 的服务开启管理 UIRabbitMQ 端口使用一览图 使用输出最简单的 Hello World!生产者定义消费者消费消息小拓展 RabbitMQ 安装使用 安装 下载 Erlang RabbitMQ 是用这个语…...
echarts x轴名称过长tip显示全称
xAxis的axisLabel的内容如下: axisLabel: { rotate: -45, color: document.body.className.indexOf(custom-f4c46d) > -1 ? #fff : #343434, // 显示省略号操作(第一步) formatter: function (value) { var val if (value.length >…...

js和css阻塞问题
面试常见问题 css 加载会不会阻塞 js 的加载?(不会)css 加载会不会阻塞 js 的执行?(会)css 加载会不会阻塞 DOM 的解析?(不会)css 加载会不会阻塞 DOM 的渲染࿱…...
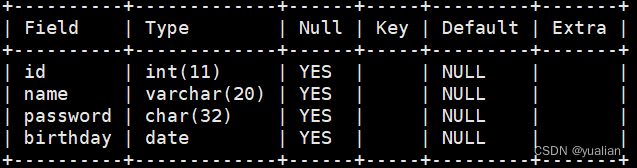
MySQL 的基础操作
数据库的基础操作 1. 库操作2. 表的操作3. 数据类型 数据库是现代应用程序中至关重要的组成部分,通过数据库管理系统(DBMS)存储和管理数据。 1. 库操作 创建数据库 创建数据库是开始使用数据库的第一步。下面是一些常见的创建数据库的示例&a…...
【python进阶篇】面向对象编程(1)
面向对象编程——Object Oriented Programming,简称OOP,是一种程序设计思想。OOP把对象作为程序的基本单元,一个对象包含了数据和操作数据的函数。 在Python中,所有数据类型都可以视为对象,当然也可以自定义对象。自定…...

力扣面试经典150 —— 6-10题
力扣面试经典150题在 VScode 中安装 LeetCode 插件即可使用 VScode 刷题,安装 Debug LeetCode 插件可以免费 debug本文使用 python 语言解题,文中 “数组” 通常指 python 列表;文中 “指针” 通常指 python 列表索引 文章目录 6. [中等] 轮转…...

[密码学]入门篇——加密方式
一、概述 加密方法主要分为两大类: 单钥加密(private key cryptography):加密和解密过程都用同一套密码双钥加密(public key cryptography):加密和解密过程用的是两套密码 历史上,…...

构建前后端分离项目常用的代码
构建前后端分离项目常用的代码 1.代码生成器 import com.baomidou.mybatisplus.generator.FastAutoGenerator;import com.baomidou.mybatisplus.generator.config.OutputFile;import com.baomidou.mybatisplus.generator.engine.FreemarkerTemplateEngine;import java.util.…...
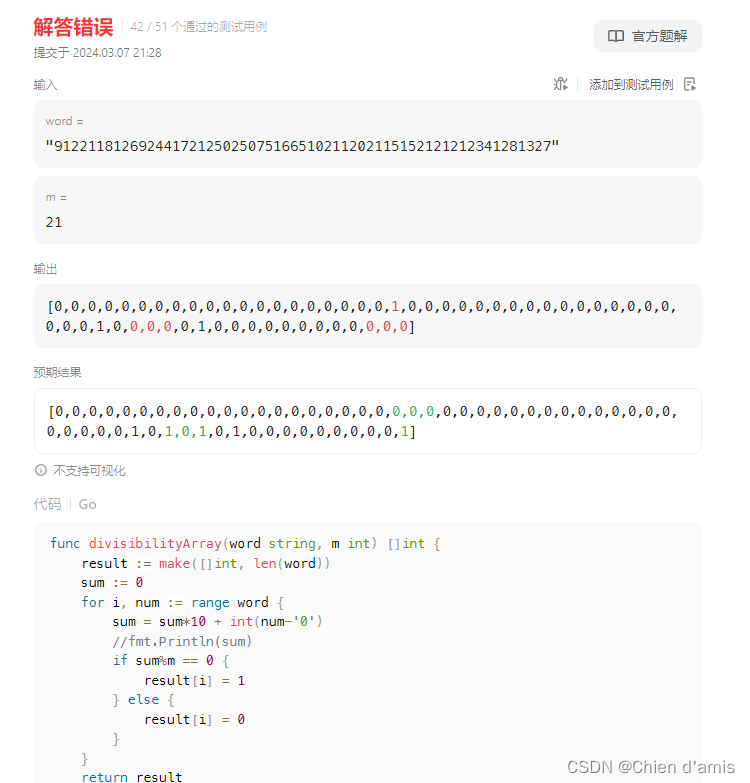
2575. 找出字符串的可整除数组(Go语言)
https://leetcode.cn/problems/find-the-divisibility-array-of-a-string/ 在看题解之前,我的代码是以下这样: package mainimport ("fmt" )func main() {fmt.Println(divisibilityArray("998244353", 3)) }func divisibilityArray…...

Redis与 Memcache区别
Redis与 Memcache区别 1 , Redis 和 Memcache 都是将数据存放在内存中,都是内存数据库。不过 Memcache 还可用于缓存 其他东西,例如图片、视频等等。 2 , Memcache 仅支持key-value结构的数据类型,Redis不仅仅支持简单的key-value类型的数据&…...
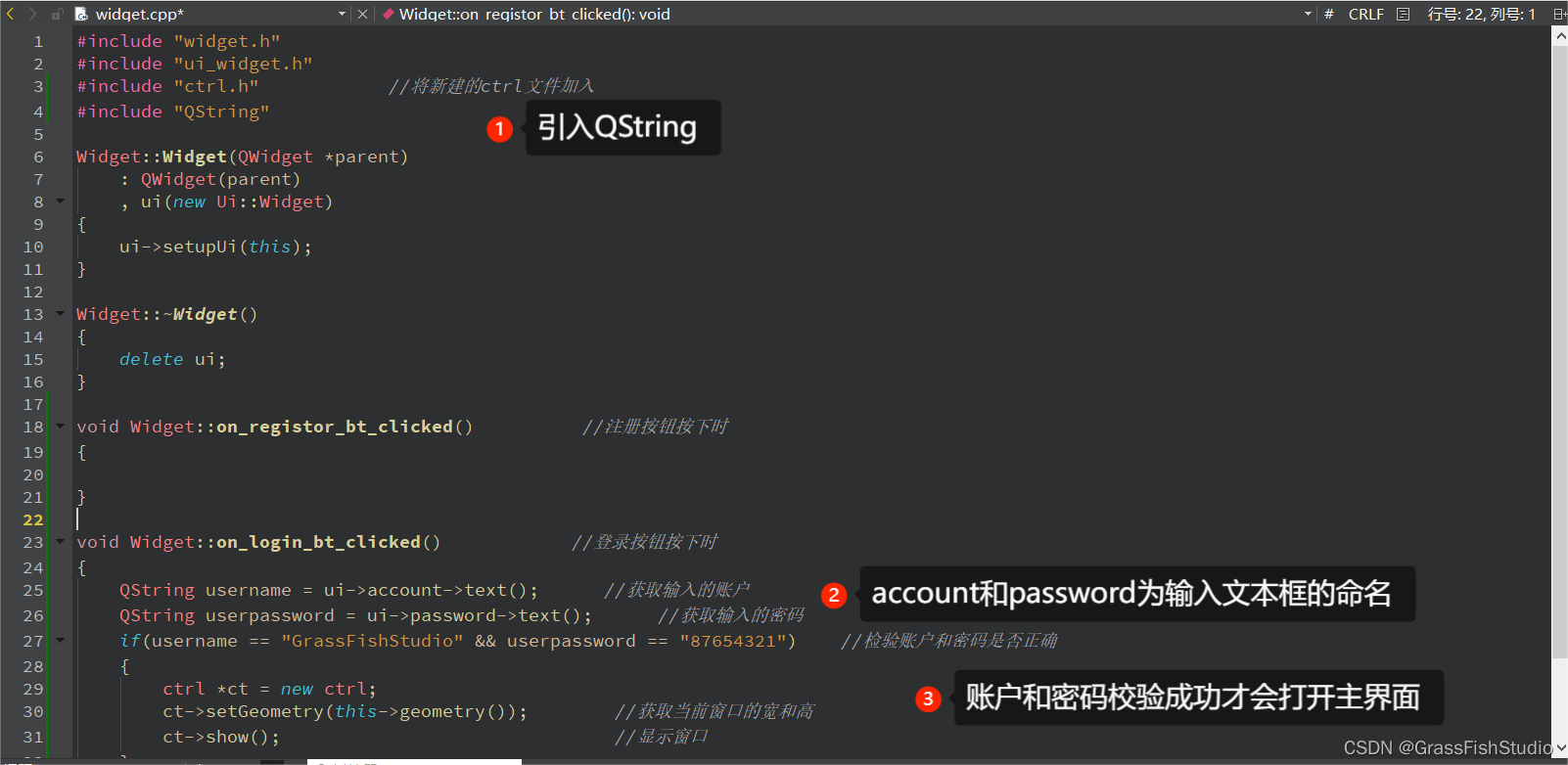
#QT(智能家居界面-界面切换)
1.IDE:QTCreator 2.实验 3.记录 (1)创建一个新界面(UI界面) (2)可以看到新加入一个ui文件,双击打开,设置窗口大小与登录界面一致 (3)加入几个PUS…...

js拓展-内置对象
目录 1. 数组对象 1.1 数组的四种方式 1.2 JS中数组的特点 1.3 常用方法 2. 日期对象 2.1 日期对象的创建 2.2 日期对象的方法 2.3 案例:输出现在的时间 3. 全局对象 3.1 字符串转换成数字类型 3.2 编码解码函数 1. 数组对象 注:数组在JS中是一…...

【李沐精读系列】GPT、GPT-2和GPT-3论文精读
论文: GPT:Improving Language Understanding by Generative Pre-Training GTP-2:Language Models are Unsupervised Multitask Learners GPT-3:Language Models are Few-Shot Learners 参考:GPT、GPT-2、GPT-3论文精读…...

Libevent的使用及reactor模型
Libevent 是一个用C语言编写的、轻量级的开源高性能事件通知库,主要有以下几个亮点:事件驱动( event-driven),高性能;轻量级,专注于网络,不如 ACE 那么臃肿庞大;源代码相当精炼、易读…...

查看Linux服务器配置
# chkconfig --list # 列出所有系统服务 # chkconfig --list | grep on # 列出所有启动的系统服务 # ifconfig # 查看所有网络接口的属性 # iptables -L # 查看防火墙设置 # route -n # 查看路由表 # netstat -lntp # 查看所有监听端口 # netstat -antp # 查看所有已经建立的连…...

【机器学习】包裹式特征选择之递归特征添加法
🎈个人主页:豌豆射手^ 🎉欢迎 👍点赞✍评论⭐收藏 🤗收录专栏:机器学习 🤝希望本文对您有所裨益,如有不足之处,欢迎在评论区提出指正,让我们共同学习、交流进…...

解决cs不能生成Linux木马的问题
要解决的问题:众所周知,msf上面的shell或者是其他的shell想反弹给cs默认情况下是只支持windows的,因为cs的监听模块默认没有linux的,但是有些主机就是用linux搭建的,这可怎么办呢。就要用到一个插件CrossC2。 下载插件…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...
