力扣面试经典150 —— 6-10题
- 力扣面试经典150题
- 在 VScode 中安装 LeetCode 插件即可使用 VScode 刷题,安装 Debug LeetCode 插件可以免费 debug
- 本文使用 python 语言解题,文中 “数组” 通常指 python 列表;文中 “指针” 通常指 python 列表索引
文章目录
- 6. [中等] 轮转数组
- 6.1 解法1:使用额外的数组
- 6.2 解法2:数组翻转
- 7. [简单] 买卖股票的最佳时机
- 7.1 解法1:暴力法
- 7.2 解法2:贪心
- 8. [中等] 买卖股票的最佳时机II
- 8.1 解法1:贪心
- 8.2 解法2:动态规划
- 9. [中等] 跳跃游戏
- 9.1 解法1:贪心模拟
- 9.2 解法2:贪心
- 10. [中等] 跳跃游戏II
- 10.1 解法1:贪心模拟
6. [中等] 轮转数组
- 题目链接
- 标签:数组、数学、双指针

6.1 解法1:使用额外的数组
- 借助一个额外数据将各个元素放到新位置。注意到从整体上看,输出数组可以看作是在
k % len(nums)位置截断然后重新组合,可以用 python 的列表操作简单地如下实现
这其实等价于用两个指针分别遍历截断的两部分,并将元素依次复制到辅助数组class Solution:def rotate(self, nums: List[int], k: int) -> None:k = k % len(nums)res = nums[-k:] + nums[:-k]nums[:] = res - 时间复杂度 O ( n ) O(n) O(n),空间复杂度 O ( n ) O(n) O(n)
6.2 解法2:数组翻转
- 和方法一一样,注意到输出数组可以看作是在
k % len(nums)位置截断然后重新组合,这可以通过三次列表翻转实现,示意如下
下面给出代码,使用双指针进行翻转操作nums = "----->-->"; k =3 result = "-->----->";reverse "----->-->" we can get "<--<-----" reverse "<--" we can get "--><-----" reverse "<-----" we can get "-->----->"class Solution:def rotate(self, nums: List[int], k: int) -> None:def _reverse(start, end):while start < end:t = nums[start]nums[start] = nums[end]nums[end] = tstart += 1end -= 1k = k % len(nums)_reverse(0, len(nums)-1)_reverse(0, k-1)_reverse(k, len(nums)-1) - 时间复杂度 O ( n ) O(n) O(n),空间复杂度 O ( 1 ) O(1) O(1)
7. [简单] 买卖股票的最佳时机
- 题目链接
- 标签:数组、动态规划

7.1 解法1:暴力法
- 直接遍历所有可能的买卖组合情况,但这种方法会超时
def maxProfit(self, prices: List[int]) -> int:# 暴力法:超时profit = -float('inf')for i in range(len(prices)-1):buy = prices[i]for j in range(i+1, len(prices)):sell = prices[j]if sell > buy and sell - buy > profit:profit = sell - buyprofit = 0 if profit < 0 else profitreturn profit - 时间复杂度 O ( n 2 ) O(n^2) O(n2),空间复杂度 O ( 1 ) O(1) O(1)
7.2 解法2:贪心
- 只遍历一遍,在每个时刻贪心地计算可能的最大利润。为此,需要动态地更新截止目前为止的最低买入价
class Solution:def maxProfit(self, prices: List[int]) -> int:# 贪心:动态维护历史最低价,进而利用它计算理论最大收益min_price = float('inf')max_profit = -float('inf')for p in prices:# 动态维护历史最低价if p < min_price:min_price = p# 基于历史最低价得到在当前时刻卖出的理论最大收益profit = p - min_priceif profit > max_profit:max_profit = profitmax_profit = 0 if max_profit < 0 else max_profitreturn max_profit - 时间复杂度 O ( n ) O(n) O(n),空间复杂度 O ( 1 ) O(1) O(1)
8. [中等] 买卖股票的最佳时机II
- 题目链接
- 标签:贪心、数组、动态规划

8.1 解法1:贪心
- 基于贪心的思想,实现最大利润意味着每一次可能的盈利都被把握。我们变量把股价曲线折线图,在每一个时刻执行收益最大化操作,即把每一个上升段都加入总收益中,水平或下降段则跳过
class Solution:def maxProfit(self, prices: List[int]) -> int:max_profit = 0for i in range(len(prices)-1):profit = prices[i+1] - prices[i]if profit > 0:max_profit += profitreturn max_profit - 时间复杂度 O ( n ) O(n) O(n),空间复杂度 O ( 1 ) O(1) O(1)
8.2 解法2:动态规划
- 题目设置满足动态规划的三要素
- 无后效性:当前和未来的交易操作不会影响过去交易操作的收益
- 最优子结构:在整个交易过程中实现最大收益,意味着交易过程中的任意一个时间段的收益都是最优的。问题最优解的结构包含其子问题的最优解
- 重叠子问题:当我们递归地自顶向下分解时,即把 “最大化前n天收益” 不断地递归分解为 “最大化前n-1天收益,同时最大化第n-1天收益” 时,出现了要在递归过程中重复求解的重叠子问题(比如 “最大化前1天收益”),这提示我们使用递推式自底向上的构造解(动态规划的自底向上形式),或使用带备忘录的递归法(动态规划的自顶向下形式)
- 我们使用自底向上的动态规划形式,这时需要构造递推公式(动态规划中称 “状态转移方程”)。定义状态
dp[i][0]和dp[i][1]分别表示第 i i i 天交易完后手里没有和持有股票的最大利润。- 对于
dp[i][0]来说,第 i i i 天交易完后手里没有股票,意味着要么前一天就没有,要么今天卖了,递推式为
d p [ i ] [ 0 ] = max { d p [ i − 1 ] [ 0 ] , d p [ i − 1 ] [ 1 ] + p r i c e s [ i ] } dp[i][0]=\max\{dp[i−1][0],dp[i−1][1]+prices[i]\} dp[i][0]=max{dp[i−1][0],dp[i−1][1]+prices[i]} - 对于
dp[i][1]来说,第 i i i 天交易完后手里有股票,意味着要么前一天有,要么今天刚买,递推式为
d p [ i ] [ 1 ] = max { d p [ i − 1 ] [ 1 ] , d p [ i − 1 ] [ 0 ] − p r i c e s [ i ] } dp[i][1]=\max\{dp[i−1][1],dp[i−1][0]−prices[i]\} dp[i][1]=max{dp[i−1][1],dp[i−1][0]−prices[i]} - 根据问题定义,第0天交易时有
d p [ 0 ] [ 0 ] = 0 , d p [ 0 ] [ 1 ] = − p r i c e s [ 0 ] dp[0][0]=0,\quad dp[0][1]=−prices[0] dp[0][0]=0,dp[0][1]=−prices[0] - 由于全部交易结束后,持有股票的收益一定低于不持有股票的收益,最后返回 d p [ n − 1 ] [ 0 ] dp[n−1][0] dp[n−1][0] 即可
- 对于
- 注意到以上状态转移方程1、2中,
dp[i]仅与dp[i-1]有关,而与更早的状态都无关,因此不必存储这些无关的状态,只需要将dp[i−1][0]和dp[i−1][1]存放在两个变量中,通过它们计算出dp[i][0]和dp[i][1]并存回对应的变量,以便于第 i + 1 i+1 i+1 天的状态转移计算即可class Solution:def maxProfit(self, prices: List[int]) -> int:dp0 = 0 # 今日交易完后手里没有股票的最大利润dp1 = -prices[0] # 今日交易完后手里有一支股票的最大利润for i in range(1, len(prices)):dp0_ = max(dp0, dp1 + prices[i])dp1_ = max(dp1, dp0 - prices[i])dp0, dp1 = dp0_, dp1_ return dp0 - 时间复杂度 O ( n ) O(n) O(n),空间复杂度 O ( 1 ) O(1) O(1)
9. [中等] 跳跃游戏
- 题目链接
- 标签:贪心、数组、动态规划

9.1 解法1:贪心模拟
- 直接模拟整个转移过程,每次都贪心地跳到能去向的最远处,直到达到终点或无法前进
class Solution:def canJump(self, nums: List[int]) -> bool:cur_pos = next_pos = 0max_range = nums[cur_pos] # 当前可达的最大索引位置while True:# 若从当前位置可以直接到目标,退出if max_range >= len(nums) - 1:return True# 考察从当前位置可达的每个新位置可覆盖的最大范围, 贪心地选择可达范围最大处作为转移到的索引位置 next_posfor steps in range(1, nums[cur_pos] + 1):next_range = cur_pos + steps + nums[cur_pos + steps]if next_range > max_range:next_pos = cur_pos + stepsmax_range = next_range# 如果当前位置已经是最佳的,且已知当前 max_range 无法到达目标,退出if next_pos == cur_pos:return False# 去向新索引位置cur_pos = next_pos - 时间复杂度 O ( n ) O(n) O(n),空间复杂度 O ( 1 ) O(1) O(1)
9.2 解法2:贪心
- 对于每一个可达位置 x x x,它使得 x + 1 , x + 2 , ⋯ , x + nums [ x ] x+1,x+2,⋯ ,x+\text{nums}[x] x+1,x+2,⋯ ,x+nums[x] 这些连续的位置都可以到达。利用贪心的思想,我们遍历数组,并在每一步维护当前可达的最大状态,如果发现最后的位置可达则返回
true,反之若遍历结束后最后位置仍不可达则返回falseclass Solution:def canJump(self, nums: List[int]) -> bool:max_range = 0for i, step in enumerate(nums):if i <= max_range:if i + step > max_range:max_range = i + stepif max_range >= len(nums) - 1:return Truereturn False - 时间复杂度 O ( n ) O(n) O(n),空间复杂度 O ( 1 ) O(1) O(1)
10. [中等] 跳跃游戏II
- 题目链接
- 标签:贪心、数组、动态规划

10.1 解法1:贪心模拟
- 和 9.1 完全一直,直接模拟整个转移过程,每次都贪心地跳到能去向的最远处,直到达到终点或无法前进。模拟的同时记录总跳跃次数并返回
class Solution:def jump(self, nums: List[int]) -> int:# 特殊情况直接退出if len(nums) == 1:return 0cur_pos = next_pos = step_cnt = 0max_range = nums[cur_pos]while True:# 若从当前位置可以直接到目标,退出if max_range >= len(nums) - 1:return step_cnt + 1# 考察每一个新位置可以覆盖的最大范围,next_pos 设置为范围最大新索引位置for steps in range(1, nums[cur_pos] + 1):next_range = cur_pos + steps + nums[cur_pos + steps]if next_range > max_range:next_pos = cur_pos + stepsmax_range = next_range# 去向新索引位置cur_pos = next_posstep_cnt += 1 - 时间复杂度 O ( n ) O(n) O(n),空间复杂度 O ( 1 ) O(1) O(1)
相关文章:

力扣面试经典150 —— 6-10题
力扣面试经典150题在 VScode 中安装 LeetCode 插件即可使用 VScode 刷题,安装 Debug LeetCode 插件可以免费 debug本文使用 python 语言解题,文中 “数组” 通常指 python 列表;文中 “指针” 通常指 python 列表索引 文章目录 6. [中等] 轮转…...

[密码学]入门篇——加密方式
一、概述 加密方法主要分为两大类: 单钥加密(private key cryptography):加密和解密过程都用同一套密码双钥加密(public key cryptography):加密和解密过程用的是两套密码 历史上,…...

构建前后端分离项目常用的代码
构建前后端分离项目常用的代码 1.代码生成器 import com.baomidou.mybatisplus.generator.FastAutoGenerator;import com.baomidou.mybatisplus.generator.config.OutputFile;import com.baomidou.mybatisplus.generator.engine.FreemarkerTemplateEngine;import java.util.…...
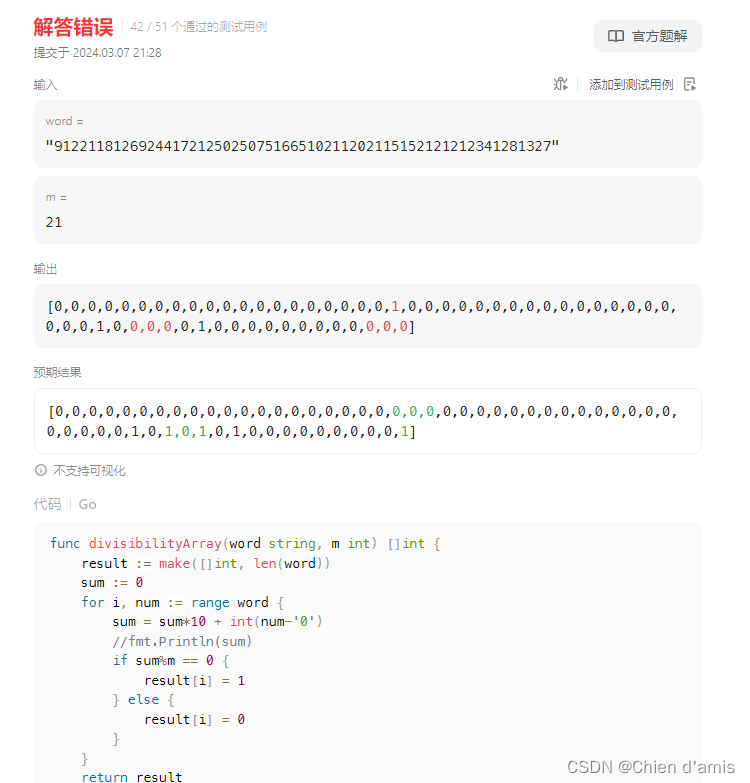
2575. 找出字符串的可整除数组(Go语言)
https://leetcode.cn/problems/find-the-divisibility-array-of-a-string/ 在看题解之前,我的代码是以下这样: package mainimport ("fmt" )func main() {fmt.Println(divisibilityArray("998244353", 3)) }func divisibilityArray…...

Redis与 Memcache区别
Redis与 Memcache区别 1 , Redis 和 Memcache 都是将数据存放在内存中,都是内存数据库。不过 Memcache 还可用于缓存 其他东西,例如图片、视频等等。 2 , Memcache 仅支持key-value结构的数据类型,Redis不仅仅支持简单的key-value类型的数据&…...
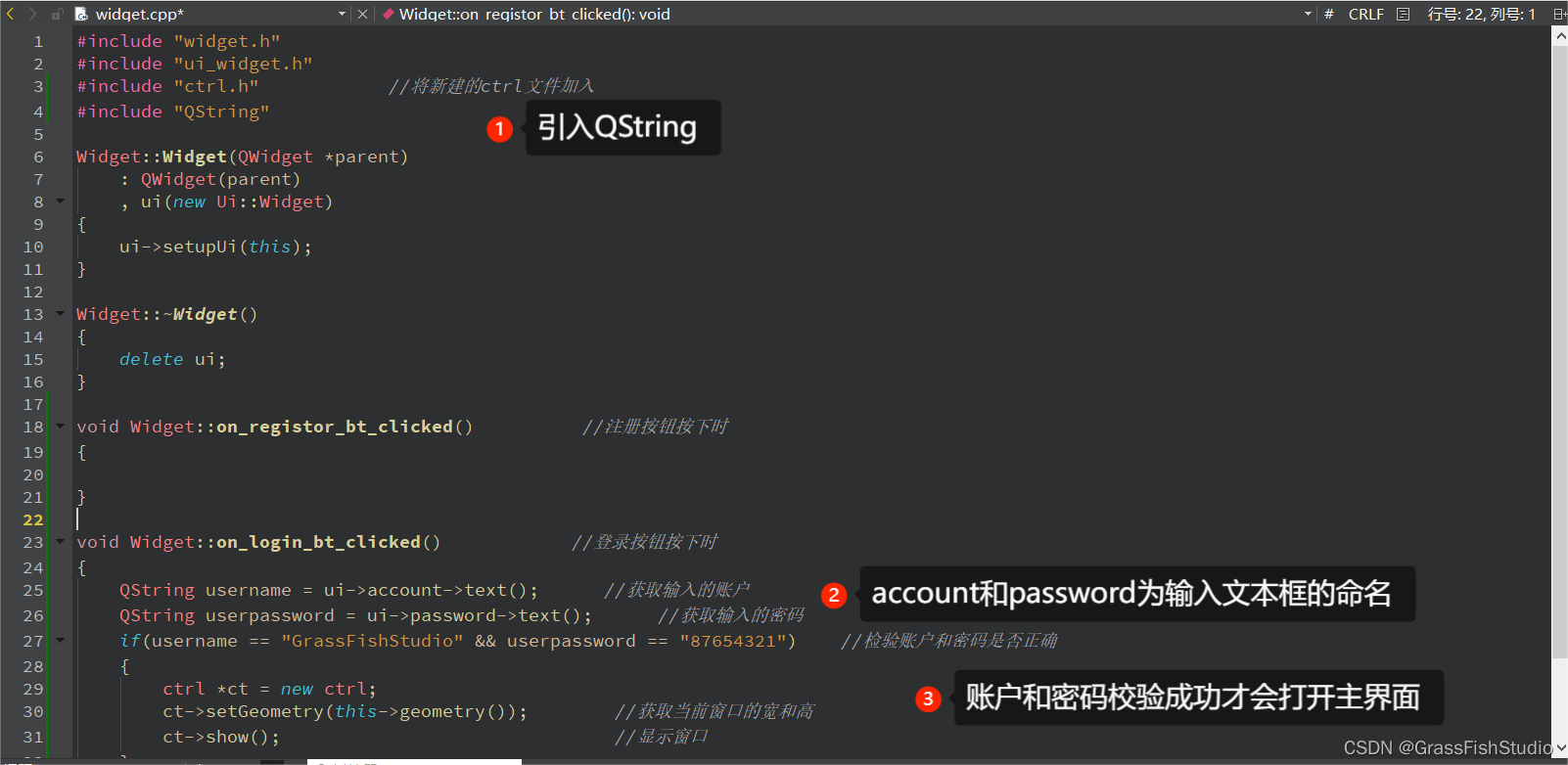
#QT(智能家居界面-界面切换)
1.IDE:QTCreator 2.实验 3.记录 (1)创建一个新界面(UI界面) (2)可以看到新加入一个ui文件,双击打开,设置窗口大小与登录界面一致 (3)加入几个PUS…...

js拓展-内置对象
目录 1. 数组对象 1.1 数组的四种方式 1.2 JS中数组的特点 1.3 常用方法 2. 日期对象 2.1 日期对象的创建 2.2 日期对象的方法 2.3 案例:输出现在的时间 3. 全局对象 3.1 字符串转换成数字类型 3.2 编码解码函数 1. 数组对象 注:数组在JS中是一…...

【李沐精读系列】GPT、GPT-2和GPT-3论文精读
论文: GPT:Improving Language Understanding by Generative Pre-Training GTP-2:Language Models are Unsupervised Multitask Learners GPT-3:Language Models are Few-Shot Learners 参考:GPT、GPT-2、GPT-3论文精读…...

Libevent的使用及reactor模型
Libevent 是一个用C语言编写的、轻量级的开源高性能事件通知库,主要有以下几个亮点:事件驱动( event-driven),高性能;轻量级,专注于网络,不如 ACE 那么臃肿庞大;源代码相当精炼、易读…...

查看Linux服务器配置
# chkconfig --list # 列出所有系统服务 # chkconfig --list | grep on # 列出所有启动的系统服务 # ifconfig # 查看所有网络接口的属性 # iptables -L # 查看防火墙设置 # route -n # 查看路由表 # netstat -lntp # 查看所有监听端口 # netstat -antp # 查看所有已经建立的连…...

【机器学习】包裹式特征选择之递归特征添加法
🎈个人主页:豌豆射手^ 🎉欢迎 👍点赞✍评论⭐收藏 🤗收录专栏:机器学习 🤝希望本文对您有所裨益,如有不足之处,欢迎在评论区提出指正,让我们共同学习、交流进…...

解决cs不能生成Linux木马的问题
要解决的问题:众所周知,msf上面的shell或者是其他的shell想反弹给cs默认情况下是只支持windows的,因为cs的监听模块默认没有linux的,但是有些主机就是用linux搭建的,这可怎么办呢。就要用到一个插件CrossC2。 下载插件…...

vue3组件通信方式
不管是vue2还是vue3,组件通信方式很重要,不管是项目还是面试都是经常用到的知识点。 vue2组件通信方式 props:可以实现父子组件、子父组件、甚至兄弟组件通信 自定义事件:可以实现子父组件通信 全局事件总线$bus:可以实现任意组件通信 pubsub:发布订阅模式实现任意组件通信…...

前端实现生成图片并批量下载,下载成果物是zip包
简介 项目上有个需求,需要根据表单填写一些信息,来生成定制的二维码图片,并且支持批量下载二维码图片。 之前的实现方式是直接后端生成二维码图片,点击下载时后端直接返回一个zip包即可。但是项目经理说后端实现方式每次改个东西…...

android 快速实现 圆角矩形控件 及 圆形控件
1.自定义RoundImageView package com.examle.widget;import android.content.Context; import android.content.res.TypedArray; import android.graphics.Bitmap; import android.graphics.Canvas; import android.graphics.Color; import android.graphics.Paint; import an…...
【Python】外网远程登录访问jupyter notebook+pycharm使用ipython
第一步:创建python虚拟环境 conda create -n py3610 python3.6.10第二步:安装ipython pip install ipython pip install ipython notebook第三步:创建 IPython Notebook 服务器配置文件 # 进入python交互shell,设置密码 >&…...

error:0308010C:digital envelope routines::unsupported
error:0308010C:digital envelope routines::unsupported 报错原因解决方案方案一:降低node版本在17以下指定node版本 mac node版本降级 mac切换node版本 方案二:启用legacy OpenSSL provider方案三:配置package.json文件拓展:pac…...
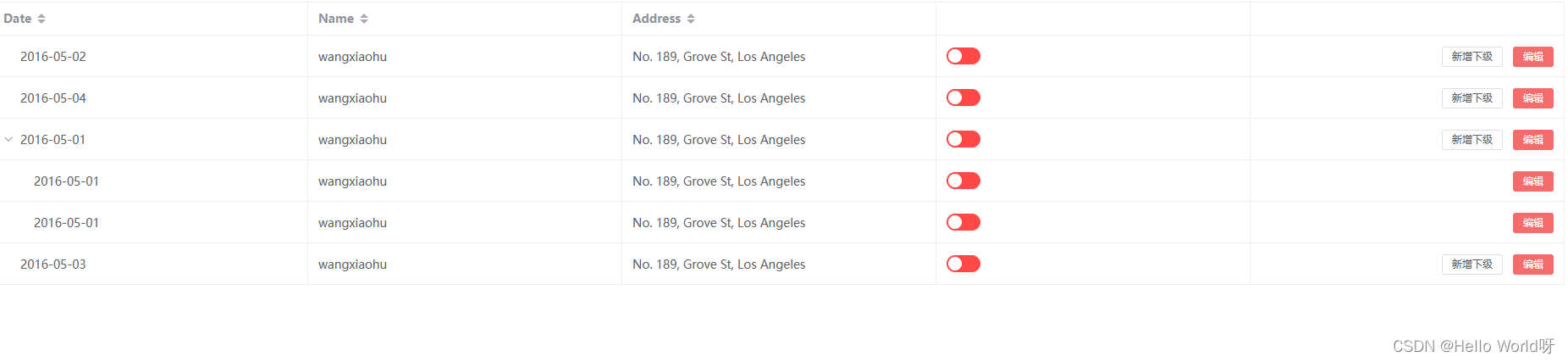
Vue前端的工作需求
加油,新时代打工人! 需求: 实现带树形结构的表格,父数据显示新增下级,和父子都显示编辑。 技术: Vue3 Element Plus <template><div><el-table:data"tableData"style"width…...

97. 常用的HTTP服务压测工具
文章目录 导言一、ab二、wrk三、go-wrk 导言 在项目正式上线之前,我们通常需要通过压测来评估当前系统能够支撑的请求量、排查可能存在的隐藏bug,同时了解了程序的实际处理能力能够帮我们更好的匹配项目的实际需求(服务器实例个数,如需要部署…...

活动预告|听云猿生数据创始人 CEO 曹伟分享云数据库行业十余年经验总结
3月16日,KubeBlocks 将携手 OceanBase 开源社区、AutoMQ 带来《LLMs 时代下的企业数据管理与降本增效之路》主题 meetup,扫描下方二维码,即刻报名👇。 云猿生数据创始人 & CEO 曹伟将带来《KubeBlocks:把所有数据…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...
