支持向量机 SVM | 线性可分:软间隔模型
目录
- 一. 软间隔模型
- 1. 松弛因子的解释
- 小节
- 2. SVM软间隔模型总结
线性可分SVM中,若想找到分类的超平面,数据必须是线性可分的;但在实际情况中,线性数据集存在少量的异常点,导致SVM无法对数据集线性划分
也就是说:正常数据本身是线性可分的,但是由于存在异常点数据,导致数据集不能够线性可分
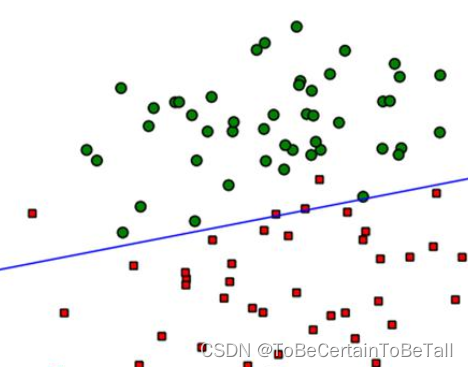
一. 软间隔模型
为了解决上述问题,我们引入软间隔的概念:
1. 松弛因子的解释
- 硬间隔: 线性划分SVM中的硬间隔是距离度量;在线性划分SVM中,要求函数距离一定是大于等于1的,最大化硬间隔条件为: { m i n 1 2 ∥ w → ∥ 2 s . t : y ( i ) ( ω T ⋅ x ( i ) + b ) ≥ 1 , i = 1 , 2 , . . . , m \left\{\begin{matrix}min\frac{1}{2}\left \| \overrightarrow{w} \right \| ^{2} \\s.t: y^{(i)} (\omega ^{T}\cdot x^{(i)} +b)\ge1,i=1,2,...,m \end{matrix}\right. {min21 w 2s.t:y(i)(ωT⋅x(i)+b)≥1,i=1,2,...,m
- 软间隔:SVM对于训练集中的每个样本都引入一个松弛因子(ξ),使得函数距离加上松弛因子后的值是大于等于1; y ( i ) ( ω T ⋅ x ( i ) + b ) ≥ 1 − ξ ; i = 1 , 2 , . . . , m , ξ ≥ 0 y^{(i)} (\omega ^{T}\cdot x^{(i)} +b)\ge1-\xi ;i=1,2,...,m,\xi\ge 0 y(i)(ωT⋅x(i)+b)≥1−ξ;i=1,2,...,m,ξ≥0
松弛因子(ξ)表示:相对于硬间隔,对样本到超平面距离的要求放松了
当 ξ = 0 ξ=0 ξ=0 , 相当于硬间隔
当 0 < ξ < 1 0<ξ<1 0<ξ<1 , 相当于样本点位于“街”内
当 ξ > 1 ξ>1 ξ>1 , 相当于样本点位于“街”对面
当 ξ > 2 ξ>2 ξ>2 , 相当于样本点位于“街”对面外侧注意: ξ ξ ξ只能对少量的样本起作用
ξ ξ ξ越大,表示样本点离超平面越近,
ξ > 1 ξ>1 ξ>1,那么表示允许该样本点分错因此:加入松弛因子是有成本的,过大的松弛因子可能会导致模型分类错误
所以,我们对存有异常点的数据集划分时,目标函数就变成了:
{ m i n 1 2 ∥ w → ∥ 2 + C ∑ i = 1 n ξ ( i ) y ( i ) ( ω T ⋅ x ( i ) + b ) ≥ 1 − ξ ( i ) , i = 1 , 2 , . . . , m \left\{\begin{matrix}min\frac{1}{2}\left \| \overrightarrow{w} \right \| ^{2}+C\sum_{i=1}^{n} \xi _{(i)} \\ \\y^{(i)} (\omega ^{T}\cdot x^{(i)} +b)\ge1-\xi ^{(i)} ,i=1,2,...,m \end{matrix}\right. ⎩ ⎨ ⎧min21 w 2+C∑i=1nξ(i)y(i)(ωT⋅x(i)+b)≥1−ξ(i),i=1,2,...,m
ξ i ≥ 0 , i = 1 , 2 , . . . , m \xi{i}\ge 0,i=1,2,...,m ξi≥0,i=1,2,...,m
公式 C ∑ i = 1 n ξ ( i ) C\sum_{i=1}^{n} \xi _{(i)} C∑i=1nξ(i)表式:
每个样本惩罚项的总和不能大,函数中的C>0是惩罚参数,需要调参C越大,表示对错误分类的惩罚越大,也就越不允许存在分错的样本;
C越小表示对误分类的惩罚越小,也就是表示允许更多的分错样本存在也就是说:
对于完全线性可分的数据来说,C的值可以给大一点
对于线性可分但存在异常的数据来说,C的值需要调小
小节
对于线性可分的m个样本(x1,y1),(x2,y2)… :
x为n维的特征向量y为二元输出,即+1,-1
SVM的输出为w,b,分类决策函数
选择一个惩罚系数C>0,构造约束优化问题
{ min β ≥ 0 1 2 ∑ i = 1 m ∑ j = 1 m β i β j y ( i ) y ( j ) x ( j ) T x ( i ) − ∑ i = 1 m β i s . t : ∑ i = 1 m β i y ( i ) = 0 , 0 ≤ β i ≤ C , i = 1 , 2 , . . . , m \left\{\begin{matrix}\min_{\beta \ge 0}\frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m} \beta _{i}\beta _{j} y^{(i)}y^{(j)}x^{(j)^{T}} x^{(i)}-\sum_{i=1}^{m} \beta _{i} \\s.t:\sum_{i=1}^{m} \beta _{i} y^{(i)}=0,0\le \beta _{i}\le C,i=1,2,...,m \end{matrix}\right. {minβ≥021∑i=1m∑j=1mβiβjy(i)y(j)x(j)Tx(i)−∑i=1mβis.t:∑i=1mβiy(i)=0,0≤βi≤C,i=1,2,...,m
使用SMO算法求出上述最优解 β \beta β
找到所有支持向量集合:
S = ( x ( i ) , y ( i ) ) ( 0 < β i < C , i = 1 , 2 , . . . , m ) S = (x^{(i)}, y^{(i)}) (0<\beta_{i} < C,i=1,2,...,m) S=(x(i),y(i))(0<βi<C,i=1,2,...,m)
从而更新w,b
w = ∑ i = 1 m β i x ( i ) y ( i ) w=\sum_{i=1}^{m} \beta _{i} x^{(i)}y^{(i)} w=∑i=1mβix(i)y(i)
b = 1 S ∑ i = 1 S ( y s − ∑ i = 1 m β i x ( i ) T y ( i ) x s ) b=\frac{1}{S} \sum_{i=1}^{S}(y^{s}- \sum_{i=1}^{m} \beta _{i} x^{(i)^{T}}y^{(i)}x^{s} ) b=S1∑i=1S(ys−∑i=1mβix(i)Ty(i)xs)
构造最终的分类器,为:
f ( x ) = s i g n ( w ∗ x + b ) f(x)=sign(w\ast x+b) f(x)=sign(w∗x+b)
x<0时,y=-1x=0时,y=0x>0时,y=1注意:假设,不会出现0若出现,正负样本随意输出一个,即+0.00000001或-0.00000001都可以
2. SVM软间隔模型总结
可以解决线性数据中存在异常点的分类模型构建问题通过引入松弛因子,可以增加模型的泛化能力,即鲁棒性;对于模型而言:如果给定的惩罚项系数C越小,表示在模型构建的时候,就允许存在越多的分类错误的样本,也就表示此时模型的准确率会比较低;如果惩罚项系数越大,表示在模型构建的时候,就越不允许存在分类错误的样本,也就表示此时模型的准确率会比较高。
感谢阅读🌼
如果喜欢这篇文章,记得点赞👍和转发🔄哦!
有任何想法或问题,欢迎留言交流💬,我们下次见!
祝愉快🌟!
相关文章:

支持向量机 SVM | 线性可分:软间隔模型
目录 一. 软间隔模型1. 松弛因子的解释小节 2. SVM软间隔模型总结 线性可分SVM中,若想找到分类的超平面,数据必须是线性可分的;但在实际情况中,线性数据集存在少量的异常点,导致SVM无法对数据集线性划分 也就是说&…...

基于Java的生活废品回收系统(Vue.js+SpringBoot)
目录 一、摘要1.1 项目介绍1.2 项目录屏 二、研究内容三、界面展示3.1 登录注册3.2 资源类型&资源品类模块3.3 回收机构模块3.4 资源求购/出售/交易单模块3.5 客服咨询模块 四、免责说明 一、摘要 1.1 项目介绍 生活废品回收系统是可持续发展的解决方案,旨在鼓…...

Linux:好用的Linux指令
进程的Linux指令 1.查看进程信息 ps ajx | head -1 && ps ajx | grep 进程名创建一个进程后输入上述代码,会打印进程信息,当我们在code.exe中写入打印pid,ppid,这里也和进程信息一致。 while :; do ps ajx | he…...

Python Tkinter GUI 基本概念
归纳编程学习的感悟, 记录奋斗路上的点滴, 希望能帮到一样刻苦的你! 如有不足欢迎指正! 共同学习交流! 🌎欢迎各位→点赞 👍 收藏⭐ 留言📝如果停止,就是低谷…...
Python实习生(自动化测试脚本开发) - 面经 - TCL新技术有限公司
JD: 招聘流程: 2024.1.3 Boss直聘 沟通 2024.1.4 约面 2024.1.6 上午面试 面试流程: 上来第一步,直接问Python基础语法,讲一下基础的数据类型 就记得元组和字典 分别具体说一下元组和字典 流程控制语句有哪些&…...
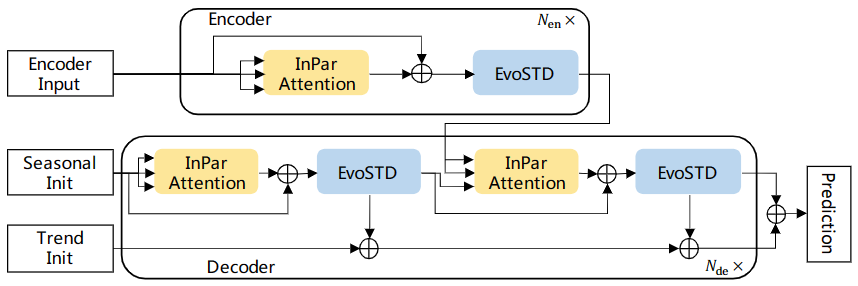
遥遥领先!基于transformer变体的时间序列预测新SOTA!
目前,以CNN、RNN和 Transformer 模型为代表的深度学习算法已经超越了传统机器学习算法,成为了时间序列预测领域一个新的研究趋向。这其中,基于Transformer架构的模型在时间序列预测中取得了丰硕的成果。 Transformer模型因其强大的序列建模能…...
Java实现从本地读取CSV文件数据
一、前言 最近项目中需要实现这样一个功能,就是从本地读取CSV文件,并以指定行作为标题行,指定行开始作为数据读取行,读取数据并返回给前端,下面具体说下是如何通过java实现。 二、如何实现? 1.引入相关mav…...
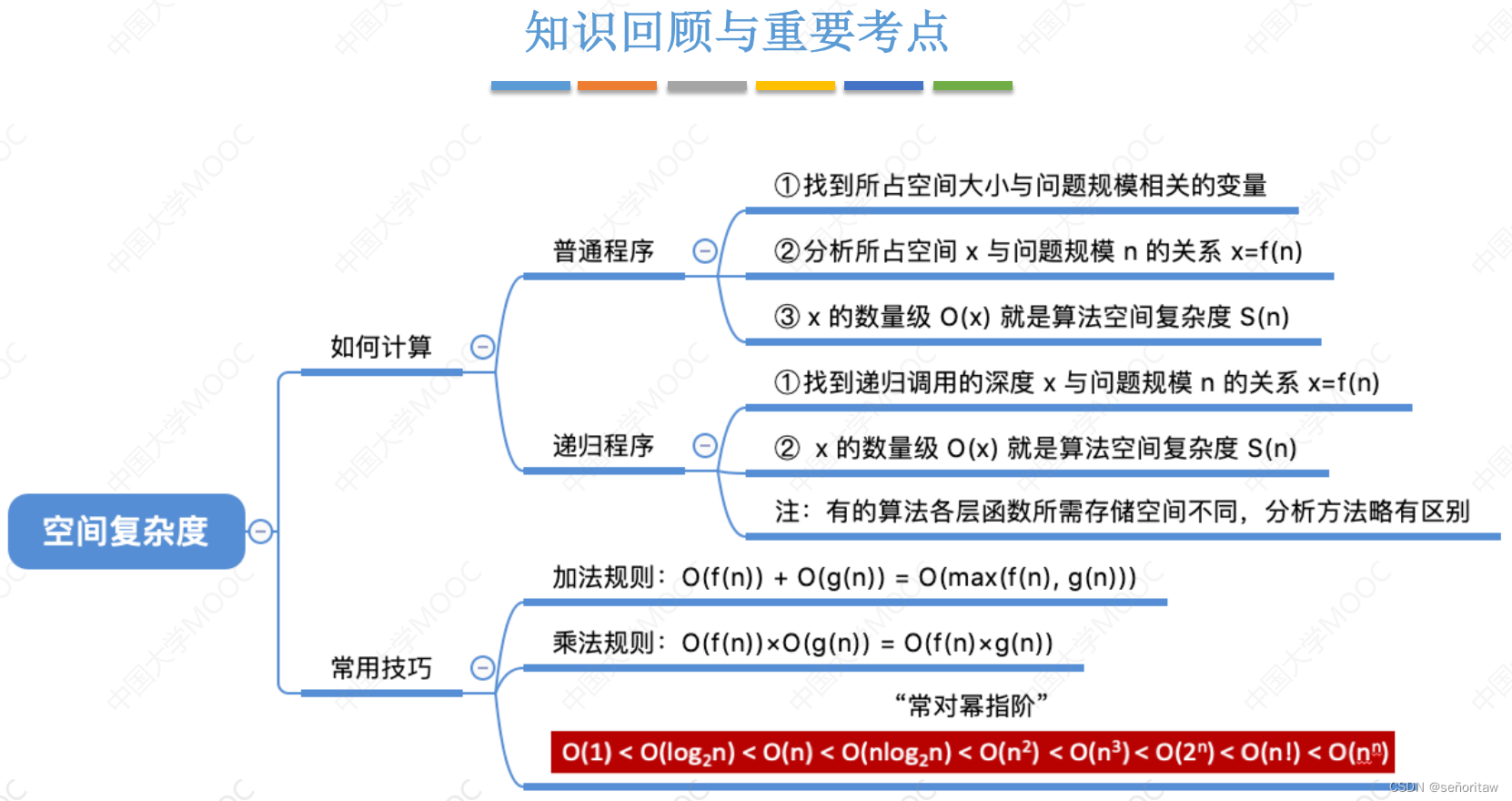
数据结构(一)——概述
一、绪论 1.1数据结构的基本概念 数据:用来描述客观事物的数、计算机中是字符及所有能输入并被程序识别和处理的符号的集合。 数据元素:数据的基本单位,一个数据元素可由若干数据项组成。 数据结构:指相互之间存在一种或多种特…...

昇腾芯片解析:华为自主研发的人工智能处理器全面分析
在当今科技发展的浪潮中,昇腾芯片作为一种新兴的处理器,正引起广泛的关注和讨论。升腾芯片究竟是由哪家公司生产的?这个问题一直困扰着许多人。下面小编将全面介绍、分析升腾芯片的生产商及各类参数、应用,以便读者对其有更全面的…...

新手做抖音小店怎么快速出体验分?教给大家一个方法!
大家好,我是电商糖果 新店怎么出体验分? 这是不是很多新店商家最苦恼事情? 因为没有体验分的店铺,平台不会给推流,开了精选联盟也没有办法带货。 总之就是运营的时候,比较受限。 那么抖音小店怎么快速出…...

Apollo决策规划 - EM planner
旨在对b站老王所讲的百度Apollo - EM planner算法做浓缩版总结 0 决策规划背景 基于图搜索 优点: 可以得到全局层面最优解,适用于比较低维数的规划问题 缺点: 规划问题维数较高时,面临指数爆炸问题 基于采样 优点:…...

Qt: 事件过滤器的更多用法
不懂事件循环怎么回事的可以看下面的文章 Qt事件循环完整流程 常规使用 定义一个窗口MainWindow ,之后在窗口里添加一个事件过滤函数eventFilter,将窗口的某一个或一些字控件安装上事件过滤器。 这种情况下MainWindow 就是pushButton11的时间过滤器&am…...

解决:ModuleNotFoundError: No module named ‘paddle‘
错误显示: 原因: 环境中没有‘paddle’的python模块,但是您在尝试导入 解决方法: 1.普通方式安装: pip install paddlepaddle #安装命令 2.镜像源安装 pip install paddlepaddle -i https://pypi.tuna.tsinghua.e…...
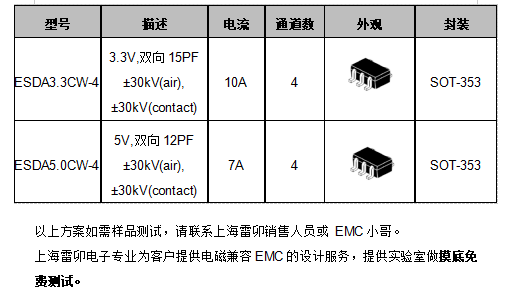
上海雷卯可以解决YPbPr/ YCbCr接口 ESD/EOS静电浪涌问题
YPbPr /YCbCr 接口传输的是视频信号,不传输音频信号。YPbPr 和 YCbCr 都是视频信号的颜色编码格式,多应用于机顶盒(Set-top box),TV电视,投影仪,游戏机和DVD播放器。 YPbPr:是一种模拟视频接口…...
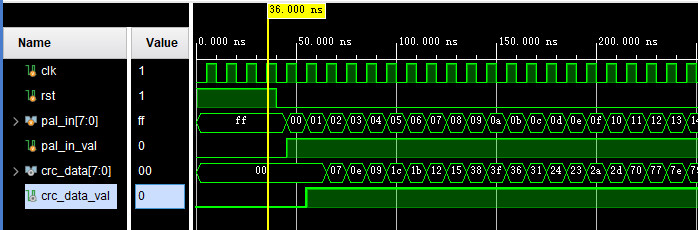
【FPGA/IC】CRC电路的Verilog实现
前言 在通信过程中由于存在各种各样的干扰因素,可能会导致发送的信息与接收的信息不一致,比如发送数据为 1010_1010,传输过程中由于某些干扰,导致接收方接收的数据却成了0110_1010。为了保证数据传输的正确性,工程师们…...
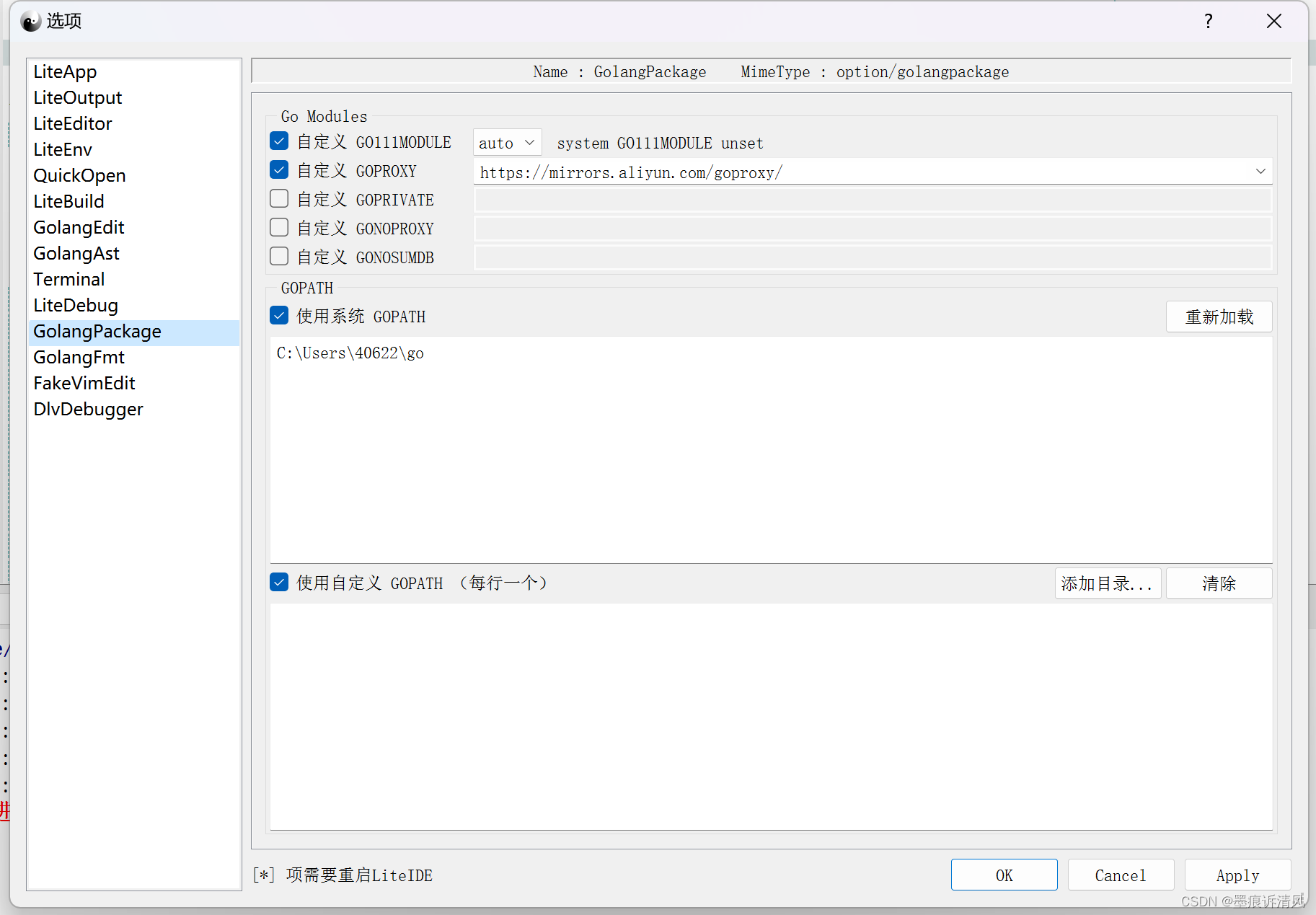
go语言添加代理
LiteIDE 工具->管理 https://mirrors.aliyun.com/goproxy/或https://goproxy.cn,direct 命令行 go env -w GOPROXYhttps://goproxy.cn,direct...
kafka 可视化工具
kafka可视化工具 随着科技发展,中间件也百花齐放。平时我们用的redis,我就会通过redisInsight-v2 来查询数据,mysql就会使用goland-ide插件来查询,都挺方便。但是kafka可视化工具就找了半天,最后还是觉得redpandadata…...

安康杯安全知识竞赛上的讲话稿
各位领导、同志们: 经过近半个月时间的准备,南五十家子镇平泉首届安康杯安全生产知识竞赛初赛在今天圆满落下帏幕,经过紧张激烈的角逐, 代表队、 代表队和 代表队分别获得本次竞赛的第一、二、三名让我们以热烈的掌声表示祝…...
python 基础知识点(蓝桥杯python科目个人复习计划59)
今日复习内容:做题 例题1:建造房屋 问题描述: 小蓝和小桥是两位年轻的建筑师,他们正在设计一座新的城市。 在这个城市中,有N条街道,每条街道上有M个位置可以建造房屋(一个位置只能建造一个房…...
LCR 179. 查找总价格为目标值的两个商品 - 力扣
1. 题目 购物车内的商品价格按照升序记录于数组 price。请在购物车中找到两个商品的价格总和刚好是 target。若存在多种情况,返回任一结果即可。 2. 示例 3. 分析 题目有说明为递增数组,所以可以利用单调性双指针解决。跟611. 有效的三角形个数为一类题…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

Spring Security 认证流程——补充
一、认证流程概述 Spring Security 的认证流程基于 过滤器链(Filter Chain),核心组件包括 UsernamePasswordAuthenticationFilter、AuthenticationManager、UserDetailsService 等。整个流程可分为以下步骤: 用户提交登录请求拦…...

Android写一个捕获全局异常的工具类
项目开发和实际运行过程中难免会遇到异常发生,系统提供了一个可以捕获全局异常的工具Uncaughtexceptionhandler,它是Thread的子类(就是package java.lang;里线程的Thread)。本文将利用它将设备信息、报错信息以及错误的发生时间都…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现指南针功能
指南针功能是许多位置服务应用的基础功能之一。下面我将详细介绍如何在HarmonyOS 5中使用DevEco Studio实现指南针功能。 1. 开发环境准备 确保已安装DevEco Studio 3.1或更高版本确保项目使用的是HarmonyOS 5.0 SDK在项目的module.json5中配置必要的权限 2. 权限配置 在mo…...

用神经网络读懂你的“心情”:揭秘情绪识别系统背后的AI魔法
用神经网络读懂你的“心情”:揭秘情绪识别系统背后的AI魔法 大家好,我是Echo_Wish。最近刷短视频、看直播,有没有发现,越来越多的应用都开始“懂你”了——它们能感知你的情绪,推荐更合适的内容,甚至帮客服识别用户情绪,提升服务体验。这背后,神经网络在悄悄发力,撑起…...

npm安装electron下载太慢,导致报错
npm安装electron下载太慢,导致报错 背景 想学习electron框架做个桌面应用,卡在了安装依赖(无语了)。。。一开始以为node版本或者npm版本太低问题,调整版本后还是报错。偶尔执行install命令后,可以开始下载…...
