DFS回溯-经典全排列问题(力扣)
前言
对于全排列问题,常用的做法是设置一个vis数组来确定位置i上的数字是否被访问,因为是全排列问题,所以不同的顺序也是不一样的排列,因此每次都是从起点开始询问**(注意起点到底是0还是1)**
46全排列(最简单的模板)
class Solution {
public:vector<int>v;//存储一个排列vector<vector<int>>ans;//答案int vis[10];void dfs(vector<int> & nums){int n = nums.size();if(v.size() == n){ans.push_back(v);return;}for(int i = 0; i < n; i++){if(vis[i])continue;vis[i] = 1;v.push_back(nums[i]);dfs(nums);v.pop_back();vis[i] = 0;}}vector<vector<int>> permute(vector<int>& nums) {dfs(nums);return ans;}};
解题思路
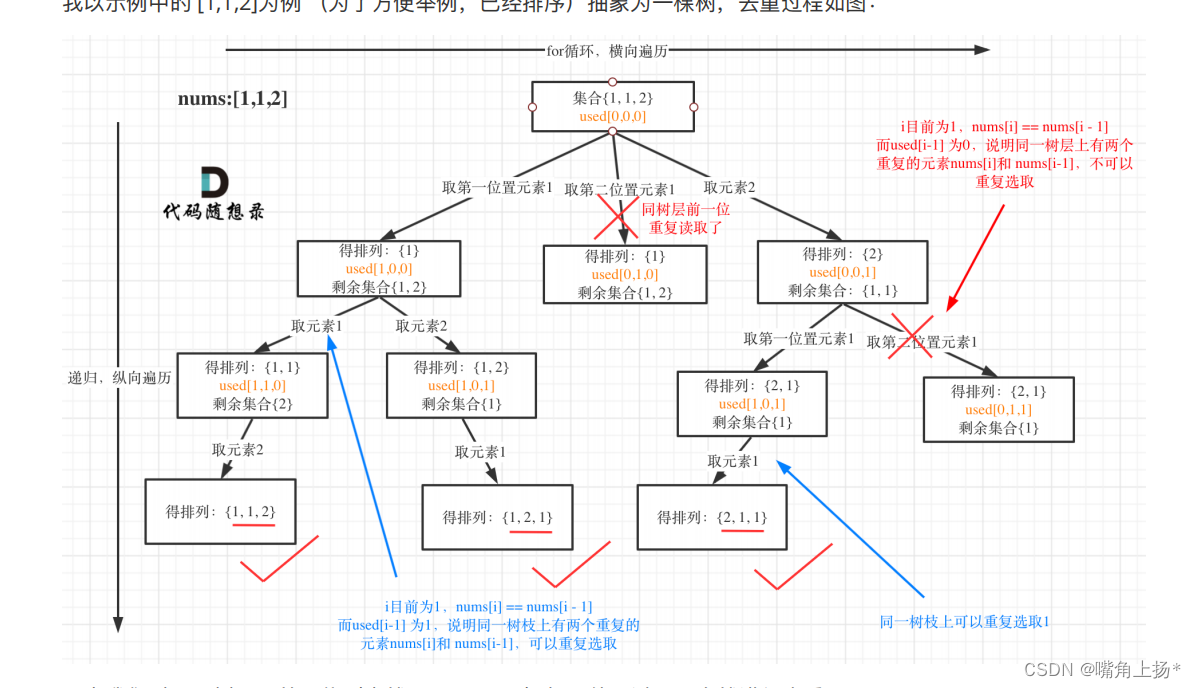
相比于全排列1,全排列2增加了重复数字,但要求不能出现重复的排列。例如原始序列1 2 1 那么全排列里 1 1 2 和 1 1 2 (两个序列的两个1位置互换了),仍然当一种排列。最好的办法就是对其进行剪枝
if(i > 0 && nums[i] == nums[i - 1] && vis[i - 1] == 0) continue;//树层去重
借鉴卡哥的一幅图,给大家看一下
(类似题目)P8605 [蓝桥杯 2013 国 AC] 网络寻路
#include<iostream>
#include<algorithm>
#include<string>
#include<vector>
#include<stack>
#include<cstdio>
#define rep(i,a,n) for(int i = a; i <= n; i++)
#define per(i,a,n) for(int i = n; i >= a; i--)using namespace std;typedef long long ll;const int N = 10010;
vector<int> v[N];
int vis[N];
int n,m;
ll ans;
vector<int>st;
void dfs(int x){int n = v[x].size();if(st.size() == 3){//因为终点位置可以和起点相同,所以当路径元素为3个的时候,就开始特判 rep(i,0, n - 1){int tp = v[x][i];if(!vis[tp] || tp == st[0]) ans++;//没被访问或者是起点 }return ;}rep(i,0,n-1){int tp = v[x][i];if(!vis[tp]){vis[tp] = 1;st.push_back(tp);dfs(tp);st.pop_back();vis[tp] = 0;}}
}int main(){cin >> n >> m;int u,vv;rep(i,1,m){cin >> u >> vv;v[u].push_back(vv);v[vv].push_back(u);}rep(i,1,n){vis[i] = 1;st.push_back(i);dfs(i);vis[i] = 0;st.pop_back();}cout << ans;return 0;}
16全排列2
//leetcode
class Solution {
public:vector<int> v;vector<vector<int>>ans;int vis[10];vector<vector<int>> permuteUnique(vector<int>& nums) {sort(nums.begin(),nums.end());dfs(nums);return ans;}void dfs(vector<int>& nums){int n = nums.size();if(v.size() == n){ans.push_back(v);return;}for(int i = 0; i < n; i++){if(vis[i])continue;if(i > 0 && nums[i] == nums[i - 1] && vis[i - 1] == 0) continue;//树层去重vis[i] = 1;v.push_back(nums[i]);dfs(nums);v.pop_back();vis[i] = 0;}}
};
解题思路
经典的回溯问题,但分解开来看就很简单了
1 初始化:
vector<vector<string>> ans;//答案
vector<string> v(n,string(n,'.'));//二维矩阵存图,vector是一个数组,每个数组元素又是string类型,所以可以看成C语言里char类型的二维数组
- 按行进行DFS递归
void dfs(int u, int n,vector<string>& v){//u代表下标为u的行if(u == n){ans.push_back(v);return;}for(int i = 0; i < n; i++){if(check(u,i,n,v)){v[u][i] = 'Q';dfs(u + 1, n,v);v[u][i] = '.';}}}
3 根据题目条件判断:不能同行 同列 同斜线,同行问题不会出现,因为咱们是按照行来递归遍历的,所以只需要判断同列 同斜线问题
int check(int x, int y,int n,vector<string> &v){for(int i = 0; i < x; i++){if(v[i][y] == 'Q') return 0;}for(int i = x - 1, j = y - 1; i >= 0&&j >= 0; i--, j--){if(v[i][j] == 'Q') return 0;}for(int i = x - 1, j = y + 1; i >= 0 && j <= n; i--,j++){if(v[i][j] == 'Q') return 0;}return 1;}
n皇后
class Solution {
public:vector<vector<string>> ans;vector<vector<string>> solveNQueens(int n) {vector<string> v(n,string(n,'.'));dfs(0,n,v);return ans;}int check(int x, int y,int n,vector<string> &v){for(int i = 0; i < x; i++){if(v[i][y] == 'Q') return 0;}for(int i = x - 1, j = y - 1; i >= 0&&j >= 0; i--, j--){if(v[i][j] == 'Q') return 0;}for(int i = x - 1, j = y + 1; i >= 0 && j <= n; i--,j++){if(v[i][j] == 'Q') return 0;}return 1;}void dfs(int u, int n,vector<string>& v){if(u == n){ans.push_back(v);return;}for(int i = 0; i < n; i++){if(check(u,i,n,v)){v[u][i] = 'Q';dfs(u + 1, n,v);v[u][i] = '.';}}}
};
22.括号生成
class Solution {
public:vector<string>ans;//dfs搜索规则// 先放左括号,左括号数量lc < n, 则放// 然后如果左括号数量大于右括号数量且右括号数量rc < n,则放右括号void dfs(int lc, int rc, int n, string s){if(lc == n && rc == n){ans.push_back(s);return;}if(lc < n) dfs(lc + 1, rc, n, s + '(');if(lc > rc && rc < n) dfs(lc, rc + 1, n , s + ')');}vector<string> generateParenthesis(int n) {dfs(0,0,n,"");return ans;}
};
79. 单词搜索
class Solution {//主要思想:id标记下一个待寻找的字母,不是的话直接不寻找,vis作为标记走过的路径,不能回头走(例三)
public:int vis[10][10];//标记使用过的位置bool flag = false;int dx[4] = {0,0,1,-1};int dy[4] = {1,-1,0,0};void dfs(string & s,vector<vector<char>>& g,int u, int v,int id){if(flag) return;if(id == s.size()){flag = true;return;}for(int i = 0; i < 4; i++){int x = u + dx[i];int y = v + dy[i];//v写成u了,卡了一阵if(x >= 0 && x < g.size() && y>= 0 && y < g[0].size() && g[x][y] == s[id]){if(vis[x][y] == 1)continue;vis[x][y] = 1;dfs(s,g,x,y,id + 1);vis[x][y] = 0;}}}bool exist(vector<vector<char>>& board, string word) {for(int i = 0; i < board.size(); i++)for(int j = 0; j < board[0].size(); j++){if(board[i][j] == word[0]){vis[i][j] = 1;dfs(word,board,i,j,1);vis[i][j] = 0;}}return flag;}
};
相关文章:

DFS回溯-经典全排列问题(力扣)
前言 对于全排列问题,常用的做法是设置一个vis数组来确定位置i上的数字是否被访问,因为是全排列问题,所以不同的顺序也是不一样的排列,因此每次都是从起点开始询问**(注意起点到底是0还是1)** 46全排列(最简单的模板) class So…...
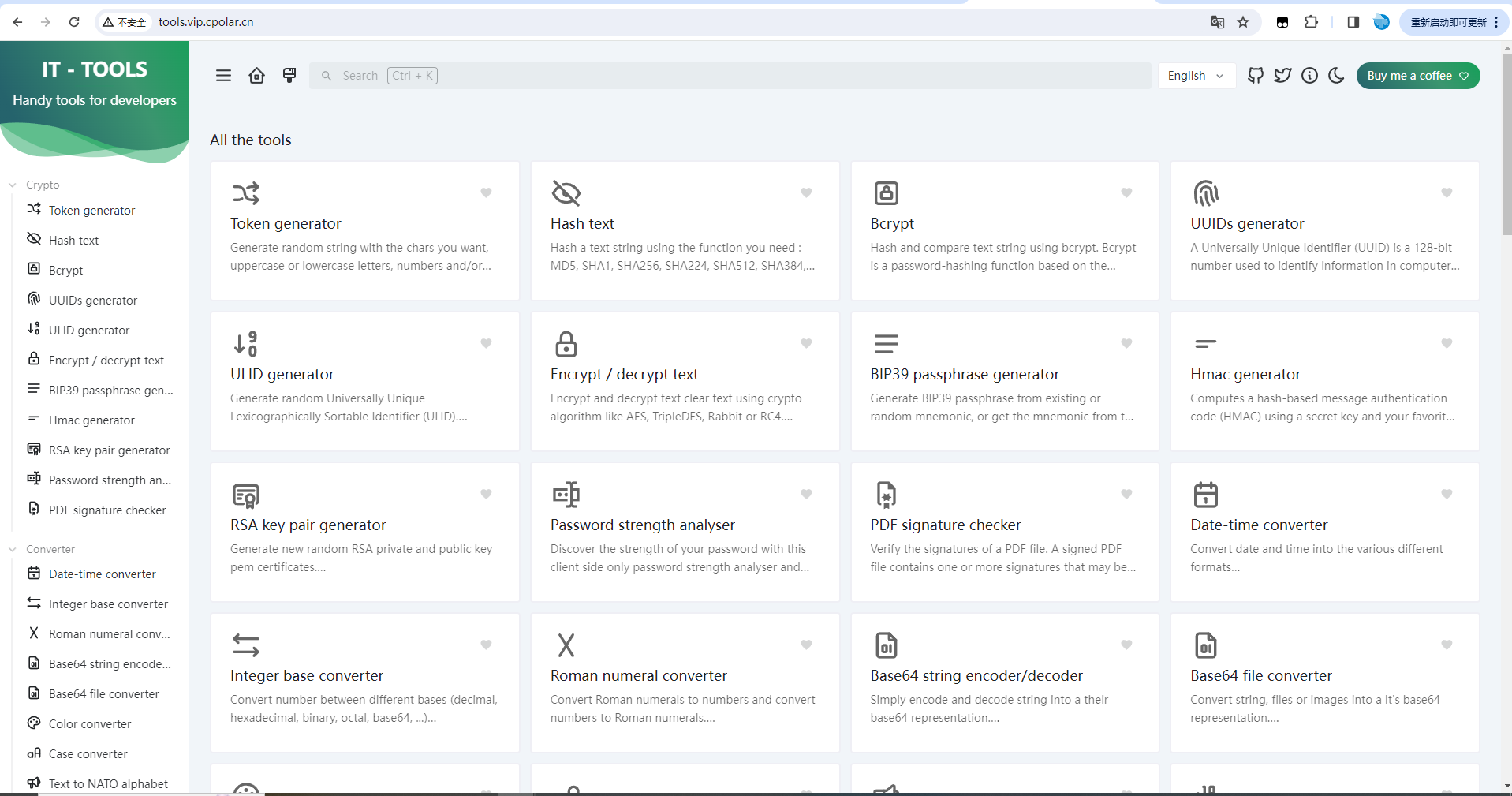
如何在Windows上使用Docker,搭建一款实用的个人IT工具箱It- Tools
文章目录 1. 使用Docker本地部署it-tools2. 本地访问it-tools3. 安装cpolar内网穿透4. 固定it-tools公网地址 本篇文章将介绍如何在Windows上使用Docker本地部署IT- Tools,并且同样可以结合cpolar实现公网访问。 在前一篇文章中我们讲解了如何在Linux中使用Docker搭…...

Linux运维_Bash脚本_编译安装ncurses-5.6
Linux运维_Bash脚本_编译安装ncurses-5.6 Bash (Bourne Again Shell) 是一个解释器,负责处理 Unix 系统命令行上的命令。它是由 Brian Fox 编写的免费软件,并于 1989 年发布的免费软件,作为 Sh (Bourne Shell) 的替代品。 您可以在 Linux 和…...

pip install和conda install的区别
先说结果:日常对于python的学习和简单项目推荐使用pip安装,效率更高,也不会有很多依赖问题。 首先,无论是conda还是pip,它们都属于包管理工具,直白点来说就是用来下载东西的。 二者的区别主要有以下几点&…...

实现video视频缓存
方法一 要实现视频被播放过后本地有缓存,下次播放无需网络即可播放,你可以利用浏览器的本地存储功能(如localStorage或IndexedDB)来实现。 你可以在视频播放结束时,将视频的URL以及相关信息存储在本地存储中。然后&a…...

Jmeter事务控制器实战
在性能测试工作中,我们往往只测试业务功能相关主要接口的数据请求和返回。然而实际上用户在使用web应用时,可能会加载诸多资源:htmldom、cssdom、javaScript、ajax请求、图片等。 从打开一个页面到界面渲染完成需要一定的加载时间࿰…...
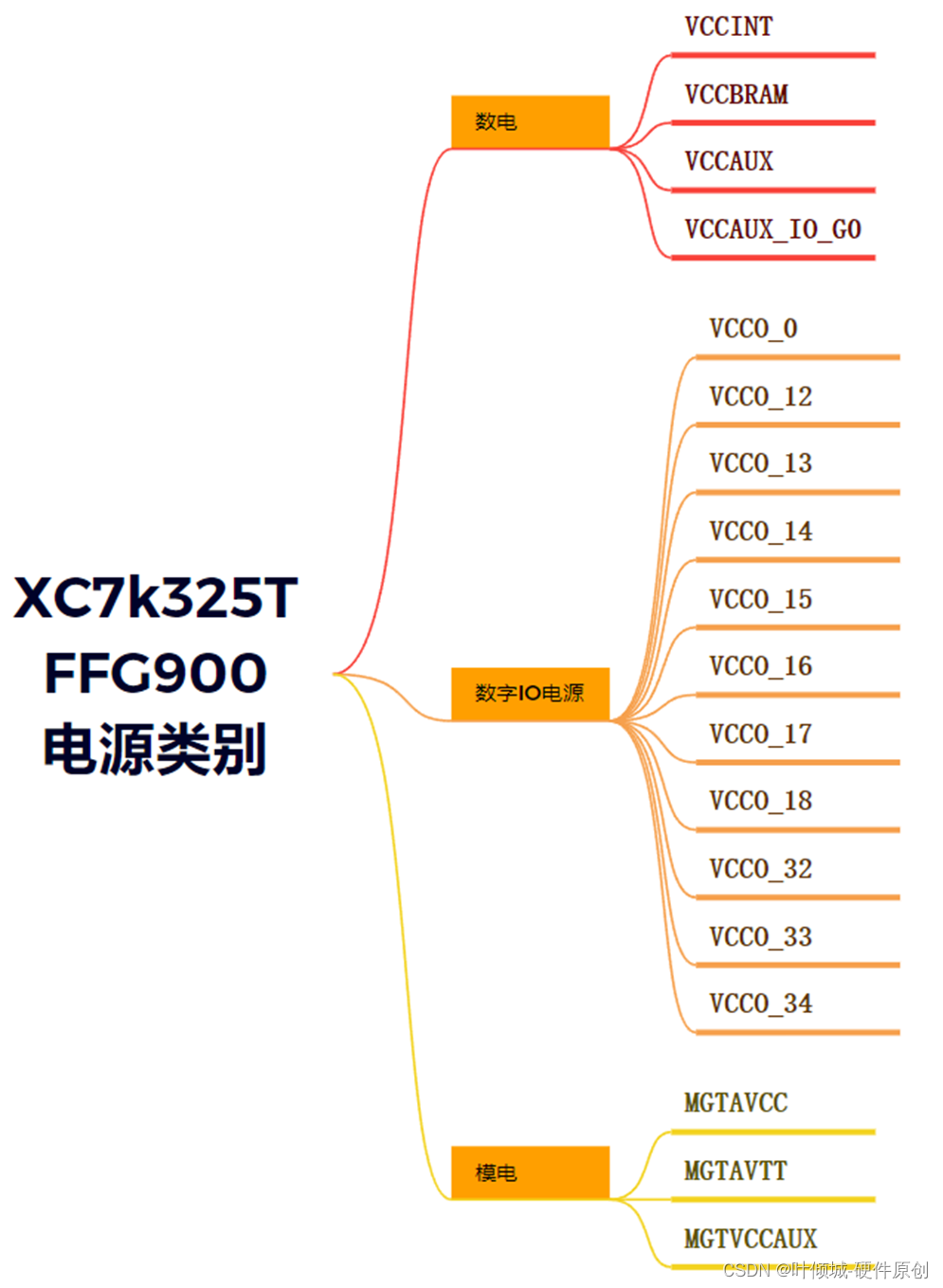
S4---FPGA-K7板级原理图硬件实战
视频链接 FPGA-K7板级系统硬件实战01_哔哩哔哩_bilibili FPGA-K7板级原理图硬件实战 基于XC7K325TFFG900的FPGA硬件实战框图 基于XILINX 的KINTEX-7 芯片XC7K325FPGA的硬件平台,FPGA 开发板挂载了4 片512MB 的高速DDR3 SDRAM 芯片,另外板上带有一个SODIM…...
input标签file属性,无法选中图片或者调用相机)
某些微信浏览器(比如小米手机mix2 8.0,Android 6:ZTE 7 max)input标签file属性,无法选中图片或者调用相机
1.初始化wxConfig (appId,timestamp,nonceStr,signatur,jsApiList) window.localStorage.setItem(currentUrl, window.location.href); 2.wx.checkJsApi({jsApiList: [chooseImage] // 需要检测的JS接口列表success: function(res) {// 以键值对的形式返回,可用的ap…...

python网络爬虫技术-mysql-5.6.39 安装
一、下载安装文件 到 MySQL官网 下载 mysql-5.6.39 压缩包链接:链接:https://pan.baidu.com/s/14e05FMhcWE8bvvStwyevNQ 提取码:1234 参考安装教程...
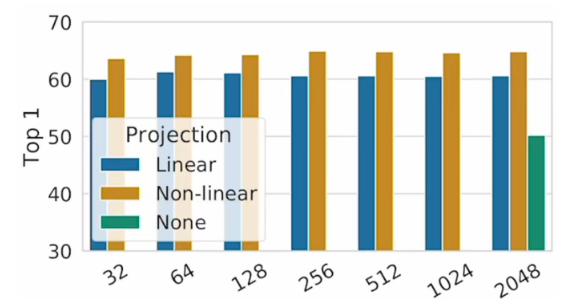
Projection head与使用例子
概念介绍 在深度学习中,Projection head是一种用于提取特征或表征的网络结构。它通常是一个或多个全连接层,将输入的高维特征映射到一个低维的向量空间,以便于进行后续的任务,如对比学习、聚类、分类等。 Projection head的使用…...
2024年新版CMS内容管理使用,不用回退老版本 使用最新小程序云开发cms内容模型
一,问题描述 最近越来越多的同学找石头哥,说cms用不了,其实是小程序官方最近又搞大动作了,偷偷的升级的云开发cms(内容管理)以下都称cms,不升级不要紧,这一升级,就导致我…...

MySql--死锁
一、什么是mysql死锁? MySQL中的死锁是指多个事务同时请求对同一资源进行操作(读或写),并且由于资源被互斥地锁定,导致彼此无法继续进行。当发生死锁时,MySQL会自动选择其中一个事务作为死锁的牺牲者,回滚该事务,并释放锁定的资源,从而解除死锁。 以下是一些处理MyS…...
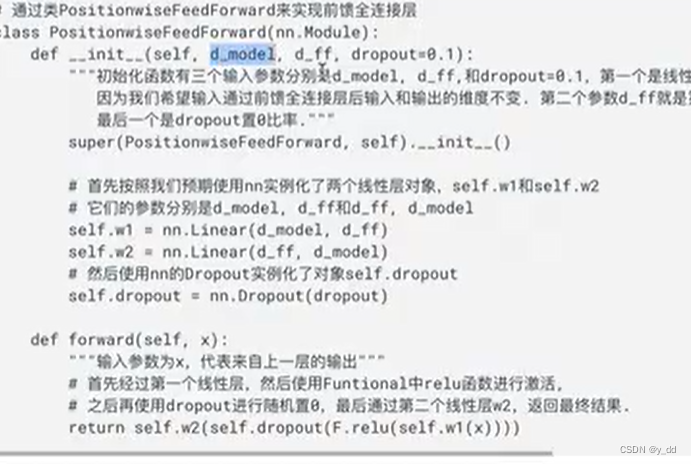
【自然语言处理六-最重要的模型-transformer-上】
自然语言处理六-最重要的模型-transformer-上 什么是transformer模型transformer 模型在自然语言处理领域的应用transformer 架构encoderinput处理部分(词嵌入和postional encoding)attention部分addNorm Feedforward & add && NormFeedforw…...
)
开发一个带有Servlet的webapp(重点)
【具体步骤如下】 ①在webapps目录下新建一个目录,起名crm(这个crm就是webapp的名字)。当然,也可以是其他目录,名字自拟 注意:crm就是这个webapp的根 ②在webapp的根下新建一个目录:WEB…...
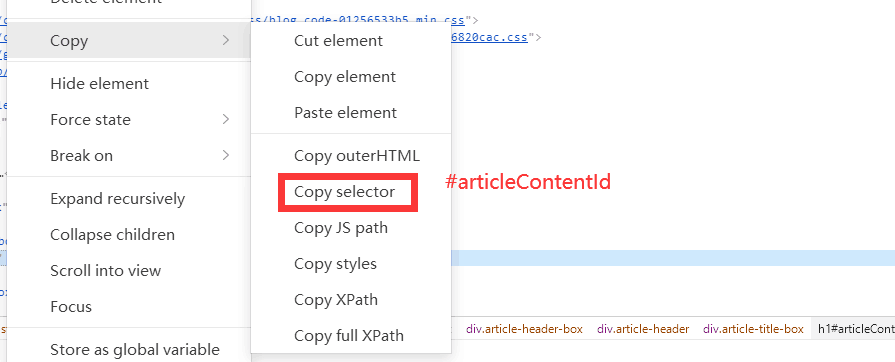
根据xlsx文件第一列的网址爬虫
seleniumXpath 在与该ipynb文件同文件下新增一个111.xlsx,第一列放一堆需要爬虫的同样式网页 然后使用seleniumXpath爬虫 from selenium import webdriver from selenium.webdriver.common.by import By import openpyxl import timedef crawl_data(driver, url)…...

【Linux】 yum —— Linux 的软件包管理器
Linux 的软件包管理器 yum yum 是什么什么是软件包查看软件包 yum 命令行工具yum 配置文件yum 凭什么可以支持下载呢?yum 生态yum 社区yum 的故障排除和资源支持yum 的持续集成和持续交付 yum 是什么 Yum(Yellowdog Updater Modified)是一个…...
及部分求值)
函数柯里化(function currying)及部分求值
函数柯里化(function currying) currying又称部分求值。一个currying的函数首先会接受一些参数,接受了这些参数之后,该函数并不会立即求值,而是继续返回另外一个函数,刚才传入的参数在函数形成的闭包中被保…...

R语言简介、环境与基础语法及注释
R语言是一种功能强大的开源统计分析语言和编程环境。它提供了丰富的数据处理、数据可视化和统计分析函数,适用于各种数据分析和建模任务。 R语言的环境主要包括R编程环境和RStudio集成开发环境(IDE)。R编程环境是R语言的核心,它提…...

React报错 之 Objects are not valid as a React child
原文链接: 1、React报错之Objects are not valid as a React child 2、Objects are not valid as a React child error [Solved] 作者:Borislav Hadzhiev 以下文中涉及到的链接均来自于该作者,他写了很多相关的文章,可以多看看他的…...
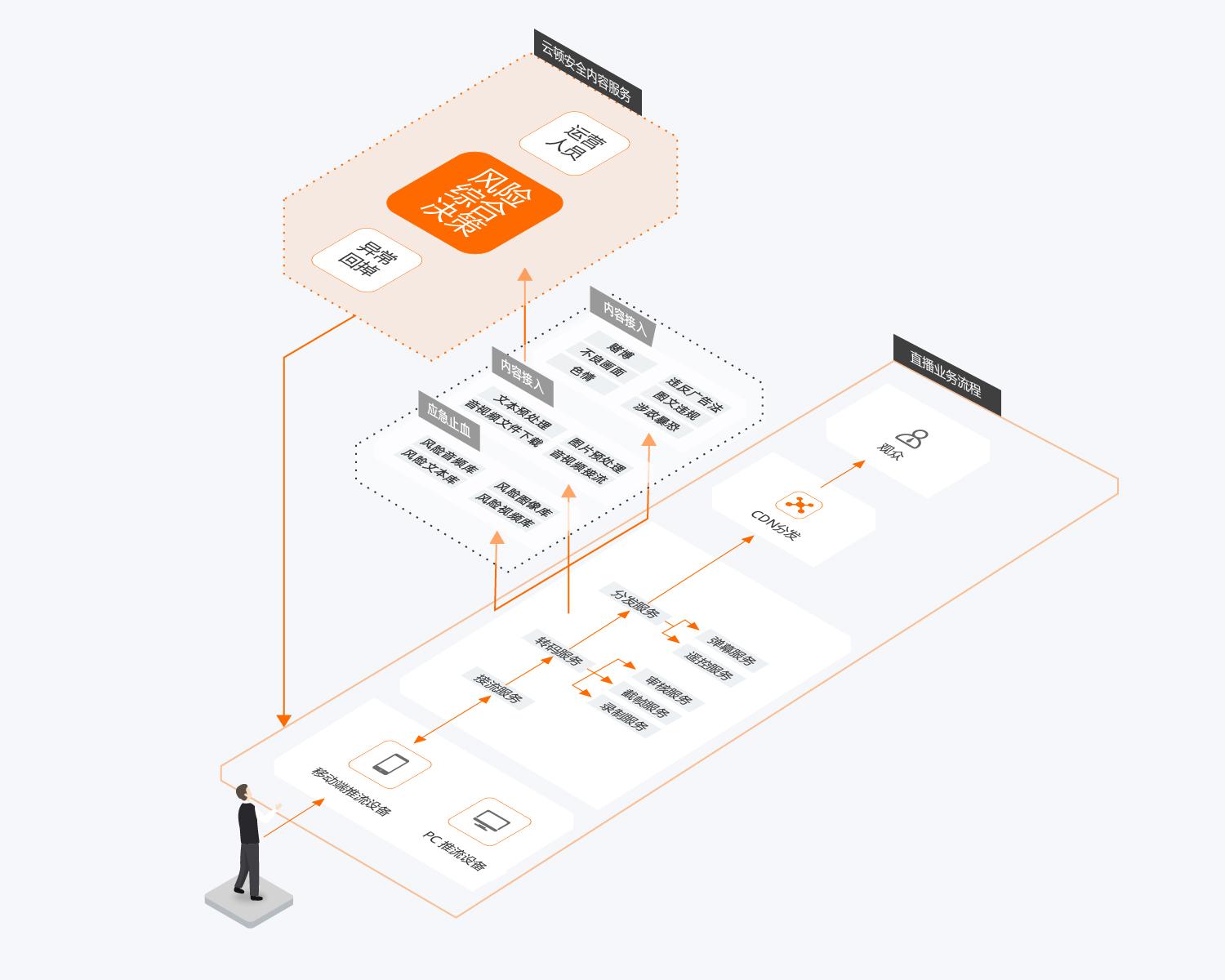
看一看阿里云,如何把抽象云概念,用可视化表达出来。
云数据库RDS_关系型数据库 云数据库RDS_关系型数据库 专有宿主机 云数据库RDS_关系型数据库_MySQL源码优化版 内容协作平台CCP-企业网盘协同办公-文件实时共享...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...
