最短路径(2.19)
目录
1.网络延迟时间
弗洛伊德算法
迪杰斯特拉算法
2. K 站中转内最便宜的航班
3.从第一个节点出发到最后一个节点的受限路径数
4.到达目的地的方案数
1.网络延迟时间
有 n 个网络节点,标记为 1 到 n。
给你一个列表 times,表示信号经过 有向 边的传递时间。 times[i] = (ui, vi, wi),其中 ui 是源节点,vi 是目标节点, wi 是一个信号从源节点传递到目标节点的时间。
现在,从某个节点 K 发出一个信号。需要多久才能使所有节点都收到信号?如果不能使所有节点收到信号,返回 -1 。
示例 1:
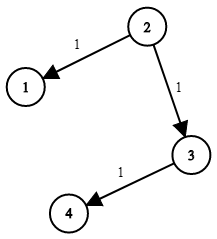
输入:times = [[2,1,1],[2,3,1],[3,4,1]], n = 4, k = 2 输出:2
示例 2:
输入:times = [[1,2,1]], n = 2, k = 1 输出:1
示例 3:
输入:times = [[1,2,1]], n = 2, k = 2 输出:-1
提示:
1 <= k <= n <= 1001 <= times.length <= 6000times[i].length == 31 <= ui, vi <= nui != vi0 <= wi <= 100- 所有
(ui, vi)对都 互不相同(即,不含重复边)
分析:要求最快能到达所有点,就是要找到这个点到达所有点的最短路径的最大值,用弗洛伊德算法的话就是比较暴力了,算出来所有的以后在需要的顶点找最大值,但是迪杰斯特拉算法少一层循环,只要这个顶点到记录到所有顶点的最小距离就好
弗洛伊德算法用邻接矩阵的时候,可以直接在邻接矩阵上操作,不用再利用结构体去建图
弗洛伊德算法
分析:要更新邻接矩阵,需要一个中间点,写在三层循环的最外层
#include <bits/stdc++.h>
using namespace std;
main()
{//接受数据int arc,n;cin>>n>>arc;int i,j,s[n][n];for(i=0; i<n; i++)for(j=0; j<n; j++){if(j!=i) s[i][j]=99999;else s[i][j]=0;}int a,b,c;for(i=0; i<arc; i++){cin>>a>>b>>c;s[a-1][b-1]=c;}cin>>a;a=a-1;//三层循环for(b=0; b<n; b++){for(i=0; i<n; i++){for(j=0; j<n; j++)s[i][j]=min(s[i][j],s[i][b]+s[b][j]);}}int ans=0;for(i=0; i<n; i++)ans=max(ans,s[a][i]);
// for(i=0; i<n; i++)
// {
// for(j=0; j<n; j++)
// cout<<s[i][j]<<" ";
// cout<<endl;
// }ans=ans>9999?-1:ans;cout<<ans;}
迪杰斯特拉算法
分析:找到了一个讲迪杰斯特拉算法的文章,讲的挺详细的【C++】Dijkstra算法_dijkstra c++-CSDN博客
先从邻接矩阵开始写,要设置好visit[](做标记)和dist[](记录最短距离),从0开始循环n遍,保证每个点都可以做一次中间点,找到最短的且未被标记的,然后以她作为中间点更新
#include <bits/stdc++.h>
using namespace std;
main()
{//接收数据int arc,n;cin>>n>>arc;int i,j,k,s[n][n];for(i=0; i<n; i++)for(j=0; j<n; j++){if(j!=i) s[i][j]=99999;else s[i][j]=0;}int a,b,c;for(i=0; i<arc; i++){cin>>a>>b>>c;s[a-1][b-1]=c;}for(i=0; i<n; i++){for(j=0; j<n; j++){cout<<s[i][j]<<" ";}cout<<endl;}cin>>a;//迪杰斯特拉int visit[n],dist[n];memset(visit,0,sizeof(visit));memset(dist,9999,sizeof(dist));dist[a-1]=0;dist[-1]=9999;//循环n遍for(i=0; i<n; i++){j=-1;//计算最小for(k=0; k<n; k++){if(!visit[k]&&dist[k]<=dist[j])j=k;}//做标记visit[j]=1;//更新路径for(k=0; k<n; k++){dist[k]=min(dist[k],dist[j]+s[j][k]);}for(k=0;k<n;k++) cout<<dist[k]<<" ";cout<<endl;}int ans=0;for(i=0; i<n; i++){ans=max(ans,dist[i]);}ans=ans>9999?-1:ans;cout<<ans;}
2. K 站中转内最便宜的航班
有 n 个城市通过一些航班连接。给你一个数组 flights ,其中 flights[i] = [fromi, toi, pricei] ,表示该航班都从城市 fromi 开始,以价格 pricei 抵达 toi。
现在给定所有的城市和航班,以及出发城市 src 和目的地 dst,你的任务是找到出一条最多经过 k 站中转的路线,使得从 src 到 dst 的 价格最便宜 ,并返回该价格。 如果不存在这样的路线,则输出 -1。
示例 1:
输入: n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]] src = 0, dst = 2, k = 1 输出: 200 解释: 城市航班图如下
从城市 0 到城市 2 在 1 站中转以内的最便宜价格是 200,如图中红色所示。
示例 2:
输入: n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]] src = 0, dst = 2, k = 0 输出: 500 解释: 城市航班图如下 从城市 0 到城市 2 在 0 站中转以内的最便宜价格是 500,如图中蓝色所示。
提示:
1 <= n <= 1000 <= flights.length <= (n * (n - 1) / 2)flights[i].length == 30 <= fromi, toi < nfromi != toi1 <= pricei <= 104- 航班没有重复,且不存在自环
0 <= src, dst, k < nsrc != dst
分析:我想到的时用迪杰斯特拉算法,在计算的过程中记录中转次数进行剪枝,比较容易出错的点就是可以中专k次,但是直接到达的算是中转0次,但是如果是原点和终点在同一个地方的话要比0次少一次,那就是-1次,但是我设置的是从原点到原点是0次,所以可以理解成到达某个地方需要乘坐几次航班,那就是乘坐k+1次时才算中转k次,这里比较容易出错
#include <bits/stdc++.h>
using namespace std;
main()
{int arc,n;cin>>n>>arc;int i,j,k,s[n][n];for(i=0; i<n; i++)for(j=0; j<n; j++){if(j!=i) s[i][j]=99999;else s[i][j]=0;}int a,b,c;for(i=0; i<arc; i++){cin>>a>>b>>c;s[a][b]=c;}
// for(i=0; i<n; i++)
// {
// for(j=0; j<n; j++)
// {
// cout<<s[i][j]<<" ";
// }
// cout<<endl;
// }cin>>a>>b>>c;int visit[n],dist[n],ans[n];memset(visit,0,sizeof(visit));memset(dist,9999,sizeof(dist));memset(ans,0,sizeof(ans));dist[a]=0;dist[-1]=9999;for(i=0;i<n;i++){j=-1;for(k=0;k<n;k++){if(!visit[k]&&dist[k]<=dist[j]) j=k;}visit[j]=1;for(k=0;k<n;k++){if(dist[k]>dist[j]+s[j][k] && ans[j]+1<=c+1){ans[k]=ans[j]+1;dist[k]=dist[j]+s[j][k];}}}// for(i=0;i<n;i++) cout<<ans[i]<<" ";cout<<dist[b];
}
3.从第一个节点出发到最后一个节点的受限路径数
现有一个加权无向连通图。给你一个正整数 n ,表示图中有 n 个节点,并按从 1 到 n 给节点编号;另给你一个数组 edges ,其中每个 edges[i] = [ui, vi, weighti] 表示存在一条位于节点 ui 和 vi 之间的边,这条边的权重为 weighti 。
从节点 start 出发到节点 end 的路径是一个形如 [z0, z1, z2, ..., zk] 的节点序列,满足 z0 = start 、zk = end 且在所有符合 0 <= i <= k-1 的节点 zi 和 zi+1 之间存在一条边。
路径的距离定义为这条路径上所有边的权重总和。用 distanceToLastNode(x) 表示节点 n 和 x 之间路径的最短距离。受限路径 为满足 distanceToLastNode(zi) > distanceToLastNode(zi+1) 的一条路径,其中 0 <= i <= k-1 。
返回从节点 1 出发到节点 n 的 受限路径数 。由于数字可能很大,请返回对 109 + 7 取余 的结果。
示例 1:

输入:n = 5, edges = [[1,2,3],[1,3,3],[2,3,1],[1,4,2],[5,2,2],[3,5,1],[5,4,10]] 输出:3 解释:每个圆包含黑色的节点编号和蓝色的 distanceToLastNode 值。三条受限路径分别是: 1) 1 --> 2 --> 5 2) 1 --> 2 --> 3 --> 5 3) 1 --> 3 --> 5
示例 2:
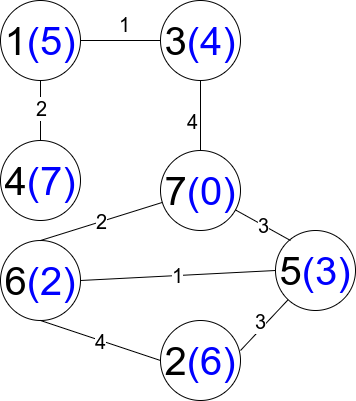
输入:n = 7, edges = [[1,3,1],[4,1,2],[7,3,4],[2,5,3],[5,6,1],[6,7,2],[7,5,3],[2,6,4]] 输出:1 解释:每个圆包含黑色的节点编号和蓝色的 distanceToLastNode 值。唯一一条受限路径是:1 --> 3 --> 7 。
提示:
1 <= n <= 2 * 104n - 1 <= edges.length <= 4 * 104edges[i].length == 31 <= ui, vi <= nui != vi1 <= weighti <= 105- 任意两个节点之间至多存在一条边
- 任意两个节点之间至少存在一条路径
分析:这个是要先算出各个点到n点的最短路径,这个的话就应该是迪杰斯特拉算法了,然后放在dist[]中记录,然后就要搜索所有的路径根据dist[]的要求去剪枝,这种搜索的话我想到的是回溯,如果这条路可以走的话进行剪枝,但是我看题解好像更多人用的是动态规划 ,直接用dp[]表示1到i的受限路径数,这样会简单很多,这样放一起来想的话,回溯更适合那种要求写出路径的,像这种只求路径数的更适合动态规划
#include <bits/stdc++.h>
using namespace std;
main()
{int arc,n;cin>>n>>arc;int i,j,k,s[n][n];for(i=0; i<n; i++)for(j=0; j<n; j++){if(j!=i) s[i][j]=9999;else s[i][j]=0;}int a,b,c;for(i=0; i<arc; i++){cin>>a>>b>>c;s[a-1][b-1]=c;s[b-1][a-1]=c;}
// for(i=0; i<n; i++)
// {
// for(j=0; j<n; j++)
// {
// cout<<s[i][j]<<" ";
// }
// cout<<endl;
// }int visit[n],dist[n],dp[n];memset(visit,0,sizeof(visit));memset(dist,9999,sizeof(dist));memset(dp,0,sizeof(dp));dist[n-1]=0;dist[-1]=9999;for(i=0;i<n;i++){j=-1;for(k=0;k<n;k++){if(!visit[k]&&dist[k]<=dist[j]) j=k;}visit[j]=1;for(k=0;k<n;k++){dist[k]=min(dist[k],dist[j]+s[j][k]);}}
// for(i=0;i<n;i++) cout<<dist[i]<<" ";cout<<endl;dp[0]=1;for(i=0;i<n;i++){for(j=i+1;j<n;j++){if(s[i][j]!=9999 && dist[i]>dist[j])dp[j]=dp[j]+dp[i];}for(k=0;k<n;k++) cout<<dp[k]<<" ";cout<<endl;}
// for(i=0;i<n;i++) cout<<dp[i]<<" ";cout<<endl;cout<<dp[n-1];
//7 8
//1 3 1
//4 1 2
//7 3 4
//2 5 3
//5 6 1
//6 7 2
//7 5 3
//2 6 4}
4.到达目的地的方案数
你在一个城市里,城市由 n 个路口组成,路口编号为 0 到 n - 1 ,某些路口之间有 双向 道路。输入保证你可以从任意路口出发到达其他任意路口,且任意两个路口之间最多有一条路。
给你一个整数 n 和二维整数数组 roads ,其中 roads[i] = [ui, vi, timei] 表示在路口 ui 和 vi 之间有一条需要花费 timei 时间才能通过的道路。你想知道花费 最少时间 从路口 0 出发到达路口 n - 1 的方案数。
请返回花费 最少时间 到达目的地的 路径数目 。由于答案可能很大,将结果对 109 + 7 取余 后返回。
示例 1:

输入:n = 7, roads = [[0,6,7],[0,1,2],[1,2,3],[1,3,3],[6,3,3],[3,5,1],[6,5,1],[2,5,1],[0,4,5],[4,6,2]] 输出:4 解释:从路口 0 出发到路口 6 花费的最少时间是 7 分钟。 四条花费 7 分钟的路径分别为: - 0 ➝ 6 - 0 ➝ 4 ➝ 6 - 0 ➝ 1 ➝ 2 ➝ 5 ➝ 6 - 0 ➝ 1 ➝ 3 ➝ 5 ➝ 6
示例 2:
输入:n = 2, roads = [[1,0,10]] 输出:1 解释:只有一条从路口 0 到路口 1 的路,花费 10 分钟。
提示:
1 <= n <= 200n - 1 <= roads.length <= n * (n - 1) / 2roads[i].length == 30 <= ui, vi <= n - 11 <= timei <= 109ui != vi- 任意两个路口之间至多有一条路。
- 从任意路口出发,你能够到达其他任意路口。
分析:我刚开始只想到了要用迪杰斯特拉算法计算出最小路径,然后再用动态规划计算路径数目,但是到计算路径数目的时候被难到了,总想着要用回溯去找路径,后来看了别人的题解才的发现有一个性质是:如果是合法路径,那么在途中经过的每一个点都是以最短路径的方式到达的,也就是说,走到这里消费的时间其实就是dist[i]
那么就可以用dp[i]记录走到这里等于dist[i]的数目,然后更新dp[i]
#include <bits/stdc++.h>
using namespace std;
main()
{int arc,n;cin>>n>>arc;int i,j,k,s[n][n];for(i=0; i<n; i++)for(j=0; j<n; j++){if(j!=i) s[i][j]=9999;else s[i][j]=0;}int a,b,c;for(i=0; i<arc; i++){cin>>a>>b>>c;s[a][b]=c;s[b][a]=c;}
// for(i=0; i<n; i++)
// {
// for(j=0; j<n; j++)
// {
// cout<<s[i][j]<<" ";
// }
// cout<<endl;
// }int visit[n],dist[n],dp[n];memset(visit,0,sizeof(visit));memset(dist,9999,sizeof(dist));memset(dp,0,sizeof(dp));dist[0]=0;dist[-1]=9999;for(i=0;i<n;i++){j=-1;for(k=0;k<n;k++){if(!visit[k]&&dist[k]<=dist[j]) j=k;}visit[j]=1;for(k=0;k<n;k++){dist[k]=min(dist[k],dist[j]+s[j][k]);}}
// for(i=0;i<n;i++) cout<<dist[i]<<" ";cout<<endl;dp[0]=1;for(i=0;i<n;i++){for(j=i+1;j<n;j++){if(s[i][j]!=9999 && dist[j]==dist[i]+s[i][j])dp[j]=dp[j]+dp[i];}
// for(k=0;k<n;k++) cout<<dp[k]<<" ";
// cout<<endl;}
// for(i=0;i<n;i++) cout<<dp[i]<<" ";cout<<endl;cout<<dp[n-1];
//7 10
//0 6 7
//0 1 2
//1 2 3
//1 3 3
//6 3 3
//3 5 1
//6 5 1
//2 5 1
//0 4 5
//4 6 2}
相关文章:

最短路径(2.19)
目录 1.网络延迟时间 弗洛伊德算法 迪杰斯特拉算法 2. K 站中转内最便宜的航班 3.从第一个节点出发到最后一个节点的受限路径数 4.到达目的地的方案数 1.网络延迟时间 有 n 个网络节点,标记为 1 到 n。 给你一个列表 times,表示信号经过 有向 边的…...
vue 总结
1.vue 的生命周期 1. es6 2. vue 基本属性指令 <template><div><!--<h1>vue基本指令的使用方式</h1><a :href"url">v-bind使用链接</a><img :src"srcUrl" /><div>解决闪烁问题<p v-cloak>{{…...

深入理解TCP/IP协议:互联网通信的核心
深入理解TCP/IP协议:互联网通信的核心 在数字化时代,TCP/IP协议是支撑全球互联网通信的基石。它不仅负责数据的传输和路由,还确保了信息传递的准确性和完整性。本文将深入探讨TCP/IP协议的工作原理、结构以及它在网络编程中的应用。 TCP/IP…...

Python数据处理实战(4)-上万行log数据提取并作图进阶版
系列文章: 0、基本常用功能及其操作 1,20G文件,分类,放入不同文件,每个单独处理 2,数据的归类并处理 3,txt文件指定的数据处理并可视化作图 4,上万行log数据提取并作图进阶版&a…...
JavaWeb Tomcat启动、部署、配置、集成IDEA
web服务器软件 服务器是安装了服务器软件的计算机,在web服务器软件中,可以部署web项目,让用户通过浏览器来访问这些项目。 Web服务器是一个应用程序(软件),对HTTP协议的操作进行封装,使得程序…...
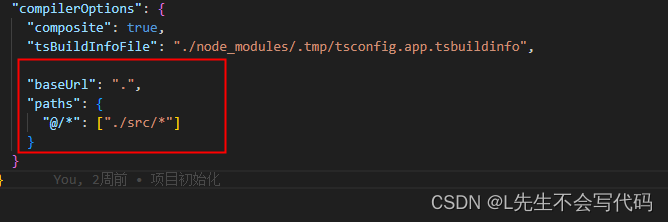
关于Vue3的一些操作
1. 设置浏览器自动打开 在package.json 中设置 dev: vite --open 2.给src文件夹配置别名 在vite.config.ts配置文件中添加以下内容 3. 如果2中有红色波浪线的问题 ***安装一个文件包***npm install types/node3. 在tsconfig.json配置文件中,找到配置项compi…...

外贸常用的出口认证 | 全球外贸数据服务平台 | 箱讯科技
出口认证是一种贸易信任背书,对许多外贸从业者而言,产品的出口认证和当前的国际贸易环境一样复杂多变,不同的目标市场、不同的产品类别,所需要的认证及标准也不同。 国际认证 01 IECEE-CB IECEE-CB体系的中文含义是“关于电工产品测试证书的相互认可体…...
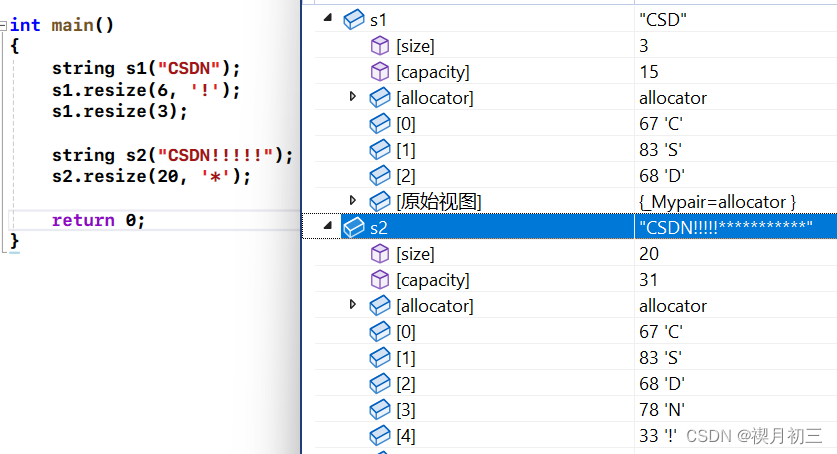
C++ 标准库类型string
C/C总述:Study C/C-CSDN博客 目录 定义和初始化string对象 string的增 使用push_back进行尾插 使用insert插入 使用append函数完成string的拼接 string的删 使用pop_back进行尾删 使用erase删除 string的查 使用find函数正向搜索第一个匹配项 使用rf…...
Material UI 5 学习02-其它按钮组件
Material UI 5 学习02-其它按钮组件 一、IconButton按钮二、 ButtonGroup按钮组1、最基本的实例2、垂直按钮组 一、IconButton按钮 图标按钮通常适用于切换按钮,允许选择或选择单个选项 取消选择,例如在项目中添加或删除星号。 <IconButton aria-lab…...

Express学习(三)
Express中间件 中间件的概念 什么是中间件 中间件,特指业务流程的中间处理环节。Express中间件的调用流程 当一个请求到达Express的服务器之后,可以连续调用多个中间件,从而对这次请求进行预处理。类似于下图所示 Express中间件的格式 Expr…...
influxdb2.0插入数据字段类型出现冲突问题解决
一、问题出现 一个学校换热站自控系统,会定时从换热站获取测点数据,并插入到influxdb数据库中。influxdb插入数据时,报错提示: com.influxdb.exceptions.UnprocessableEntityException: failure writing points to database: par…...

[C++]类和对象,explicit,static,友元,构造函数——喵喵要吃C嘎嘎4
希望你开心,希望你健康,希望你幸福,希望你点赞! 最后的最后,关注喵,关注喵,关注喵,大大会看到更多有趣的博客哦!!! 喵喵喵,你对我真的…...

物联网的商业模式洞察
大约在十年前(2014年11月),全球知名管理思想家、哈佛商学院教授迈克尔波特与PTC前首席执行官吉姆赫普尔曼,在《哈佛商业评论》上联合撰写了一篇备受赞誉的文章,题为《智能互联产品如何改变竞争》。在这篇文章中&#x…...

智能指针基础知识【C++】【RAII思想 || unique_ptr || shared_ptrweak_ptr || 循环引用问题】
目录 一,为什么需要智能指针 二,内存泄露的基本认识 1. 内存泄露分类 2. 常见的内存检测工具 3,如何避免内存泄露 三,智能指针的使用与原理 1. RAII思想 2. 智能指针 (1. unique_ptr (2. shared_…...

leetcode:反转链表II 和k个一组反转链表的C++实现
反转链表II 问题描述 给你单链表的头指针 head 和两个整数 left 和 right ,其中 left < right 。请你反转从位置 left 到位置 right 的链表节点,返回 反转后的链表 。 ListNode* reverseBetween(ListNode* head, int left, int right) {ListNode *…...

ERD Online 快速启动指南:代码下载到首次运行的全流程攻略 ️
🚀 一、代码下载 ERD online前端代码正常拉取即可👌 后端代码含有子模块,拉取命令如下: git clone --recurse-submodules https://github.com/www-zerocode-net-cn/martin-framework.git 🛠️ 二、代码构建 dz…...
c++ 11 新特性 不同数据类型之间转换函数之const_cast
一.不同数据类型之间转换函数const_cast介绍 const_cast是C11中引入的一种类型转换操作符,用于修改类型的const或volatile属性。const_cast的主要用途是移除对象的常量性,它是唯一具有此能力的C风格的转型操作符。在C11中,const_cast可以完成…...
)
C++从零开始的打怪升级之路(day45)
这是关于一个普通双非本科大一学生的C的学习记录贴 在此前,我学了一点点C语言还有简单的数据结构,如果有小伙伴想和我一起学习的,可以私信我交流分享学习资料 那么开启正题 今天分享的是关于二叉树的题目 1.根据二叉树创建字符串 606. 根…...

小鹅通前端实习一面
总时长35分钟,自我介绍开始 1.js和c特点上的差异; 2.js数组去重 3.js的数据类型 4.js的引用类型和值类型的差别 5.讲一下js的网络请求 6.对前端三件套和框架的理解 7.一个html文档的结构是怎样的 8.head和body的区别 9.一个页面的加载顺序(ht…...
ArrayList常用API
常见方法 add 增remove 删set 改get 查clear 清空元素size 长度isEmpty 为空判断 用法 // String就是泛型 这种使用方法对于限制类型很有用 ArrayList<String> arrayList new ArrayList<>();// add 添加元素 返回的是boolean 代表是否添加成功 arrayList.add(&qu…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

[论文阅读]TrustRAG: Enhancing Robustness and Trustworthiness in RAG
TrustRAG: Enhancing Robustness and Trustworthiness in RAG [2501.00879] TrustRAG: Enhancing Robustness and Trustworthiness in Retrieval-Augmented Generation 代码:HuichiZhou/TrustRAG: Code for "TrustRAG: Enhancing Robustness and Trustworthin…...
:工厂方法模式、单例模式和生成器模式)
上位机开发过程中的设计模式体会(1):工厂方法模式、单例模式和生成器模式
简介 在我的 QT/C 开发工作中,合理运用设计模式极大地提高了代码的可维护性和可扩展性。本文将分享我在实际项目中应用的三种创造型模式:工厂方法模式、单例模式和生成器模式。 1. 工厂模式 (Factory Pattern) 应用场景 在我的 QT 项目中曾经有一个需…...
