概率论小课堂：伯努利实验（正确理解随机性，理解现实概率和理想概率的偏差）
文章目录
- 引言
- I 伯努利试验
- 1.1 伯努利分布（二项式分布）
- 1.2 数学期望值（简称期望值）
- 1.3 平方差（简称方差）
- 1.4 标准差
- 1.5 小结
引言
假设买彩票中奖的概率是一百万分之一，如果要想确保成功一次，要买260万次彩票。你即使中一回大奖，花的钱要远比获得的多得多。
很多人喜欢赌小概率事件，觉得它成本低，其实由于误差的作用，要确保小概率事件发生，成本要比确保大概率事件发生高得多。
从概率论上证明了，凡事做好充足的准备，争取一次性成功，这要远比不断尝试小概率事件靠谱得多。
I 伯努利试验
出现A的概率是p，B的概率是1-p。这类试验被称为伯努利试验。
有关不确定性的规律，只有在大量随机试验时才显现出来，当试验的次数不足，它则显现出偶然性和随意性。
随机试验得到的结果，和我们用古典概率算出来的结论可能是两回事，造成试验结果和理论值不一致的原因，是试验次数太少，统计的规律性被试验的随机性掩盖了
统计学的规律只有经过了大量随机试验
相关文章：
概率论小课堂：伯努利实验（正确理解随机性，理解现实概率和理想概率的偏差）
文章目录 引言I 伯努利试验1.1 伯努利分布（二项式分布）1.2 数学期望值（简称期望值）1.3 平方差（简称方差）1.4 标准差1.5 小结引言 假设买彩票中奖的概率是一百万分之一，如果要想确保成功一次，要买260万次彩票。你即使中一回大奖，花的钱要远比获得的多得多。 很多人喜…...
加密功能实现
文章目录1. 前言2. 密码加密1. 前言 本文 主要实现 对密码进行加密 ，因为 使用 md5 容易被穷举 (彩虹表) 而破解 ，使用 spring security 框架又太大了 (杀鸡用牛刀) 。 所以本文 就自己实现一个密码加密 . 2. 密码加密 这里我们通过 加盐是方式 来 对…...
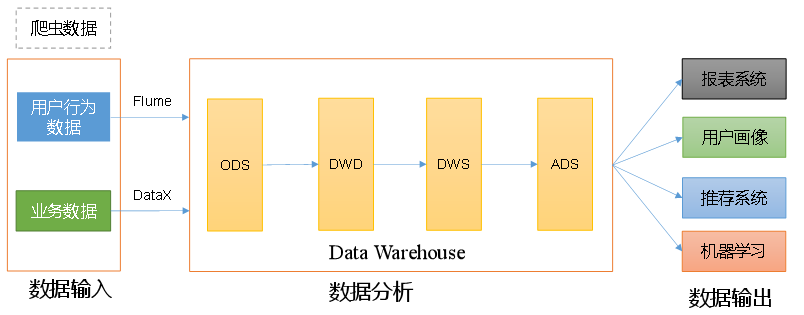
大数据项目实战之数据仓库：用户行为采集平台——第1章 数据仓库概念
第1章 数据仓库概念 数据仓库（Data Warehouse），是为企业制定决策，提供数据支持的。可以帮助企业改进业务流程、提高产品质量等。 数据仓库的输入数据通常包括：业务数据、用户行为数据和爬虫数据等 业务数据…...
NTP对时服务器（NTP电子时钟）在生物制药业应用
NTP对时服务器（NTP电子时钟）在生物制药业应用 NTP对时服务器（NTP电子时钟）在生物制药业应用 8.1 系统概述 时钟系统为生物制药厂网络控制中心调度员、车场值班员及各部门工作人员提供统一的标准时间信息，也为本工程其它…...
JPA 之 QueryDSL-JPA 使用指南
Querydsl-JPA 框架（推荐） 官网：传送门 参考： JPA整合Querydsl入门篇SpringBoot环境下QueryDSL-JPA的入门及进阶 概述及依赖、插件、生成查询实体 1.Querydsl支持代码自动完成，因为是纯Java API编写查询࿰…...
如何找回回收站删除的视频？这三种方法可以试试
在使用电脑过程中，我们可能会误删重要的文件，特别是影音文件。在这样的情况下，我们可以从计算机的回收站中找回已经被删除的视频。但是有时候，我们可能会不小心清空回收站，这时候就需要一些技巧来恢复回收站删除的视频…...
FPGA_边沿监测理解
一、简易频率计设计中为什么一定要获取下降沿?gate_a:实际闸门信号gate_a_stand:将实际闸门信号打一拍之后的信号gate_a_fall_s:下降沿标志信号cnt_clk_stand: Y值，即在实际闸门信号下，标准时钟信号的周期个数cnt_clk_stand_reg:保存Y值的寄存器核心问题…...
41 42Ping-Pong操作
提高电路吞吐率的结构——Ping-Pong操作 1.Ping-Pong操作原理 作用：为了让两个不匹配的模块进行对接，并且在对接的过程中让这两个模块能够同时工作，提高数据处理的吞吐率（也称throughput效能） 常见的不匹配࿱…...
保护你的数据安全，了解网络安全法！
网络安全法是中国自2017年6月1日起实施的一项法律，旨在保障网络安全和信息安全，维护国家安全和社会稳定。网络安全法覆盖了众多方面，包括网络基础设施安全、网络运营安全、个人信息保护、网络安全监管等，具有重要的法律意义和社会…...
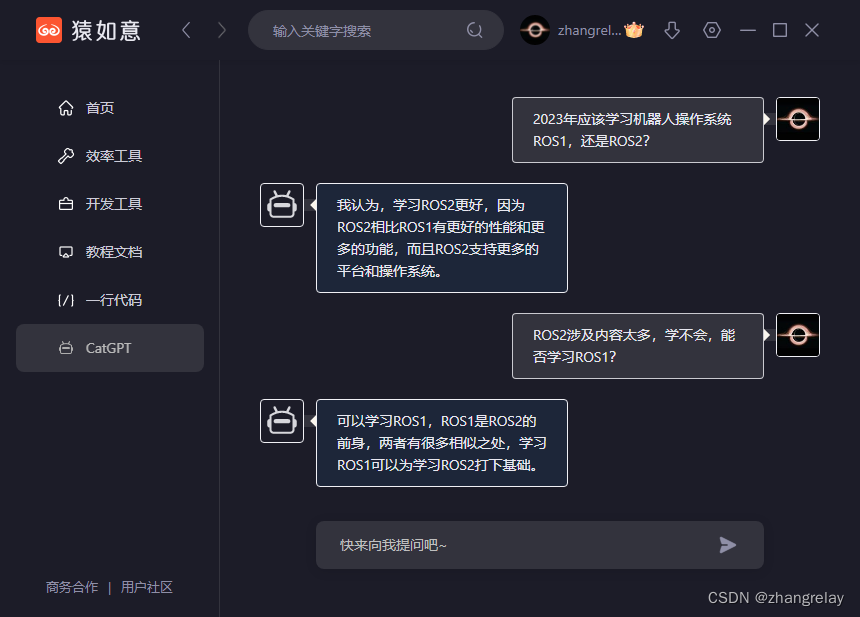
什么是CatGPT-使用效果如何-
个人使用效果，评分优，足以满足教学和填表。程序媛借助CatGPT（ChatGPT更佳），基本上可以秒杀不用此类工具的程序猿（男）！！！问：为什么使用AIGC能大幅度…...
【MySQL】第17章_触发器
第17章_触发器 在实际开发中，我们经常会遇到这样的情况：有 2 个或者多个相互关联的表，如商品信息和库存信息分别存放在 2 个不同的数据表中，我们在添加一条新商品记录的时候，为了保证数据的完整性，必须同时…...
【前端】一个更底层库-React基础知识点第2篇
目录属性状态PROPSPROP VALIDATIONSTATEFORMCONTROLLED COMPONENTSMIXINCOMPONENT APICOMPONENT LIFECYCLETOP API上一篇文章也是React基础知识点，了解到了React是什么？为什么要使用React？还知道了JSX概述，JSX嵌入变量，…...
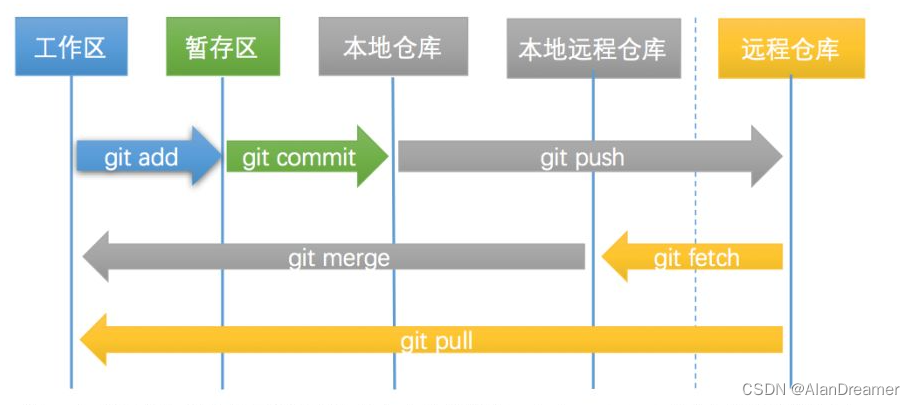
GIT基础常用命令-1
git基础常用命令-11.git简介及配置1.1 git简介1.2 git配置config1.2.1 查看配置git config1.2.2 配置设置1.2.3 获取帮助git help2 GIT基础常用命令2.1 获取镜像仓库2.1.1 git init2.1.2 git clone2.2 本地仓库常用命令2.2.1 git status2.2.2 git add2.2.3 git diff2.2.4 git c…...
02_qml_简介
qml介绍： QML是一种描述用户界面的声明式语言。它将用户界面分解成一些更小的元素，这些元素能够结合成一个组件。QML语言描述了用户界面元素的形状和行为。用户界面能够使用JavaScript来提供修饰，或者增加更加复杂的逻辑。从这个角度来看它遵循HTML-JavaScript模式，但QML是…...
小程序项目在hbuilder里面给它打包成app
小程序项目临时有些登录需求，需要把（小程序某些功能通过条件编译让它显示到app上）小程序打包成app的话就必须需要一个打包的证书，证书的话就要去重新生成，苹果电脑可以去自动生成证书，平时是用windows进行开…...
linux安装pycharm
linux安装pycharm1.下载相关软件包2. 安装步骤2.1 解压文件2.2 开启命令2.4 创建快捷方式官网链接 https://www.jetbrains.com/pycharm/download/#sectionlinux 1.下载相关软件包 找到自己下载的版本下载 2. 安装步骤 2.1 解压文件 进入压缩包路径 解压文件【我指定了解…...
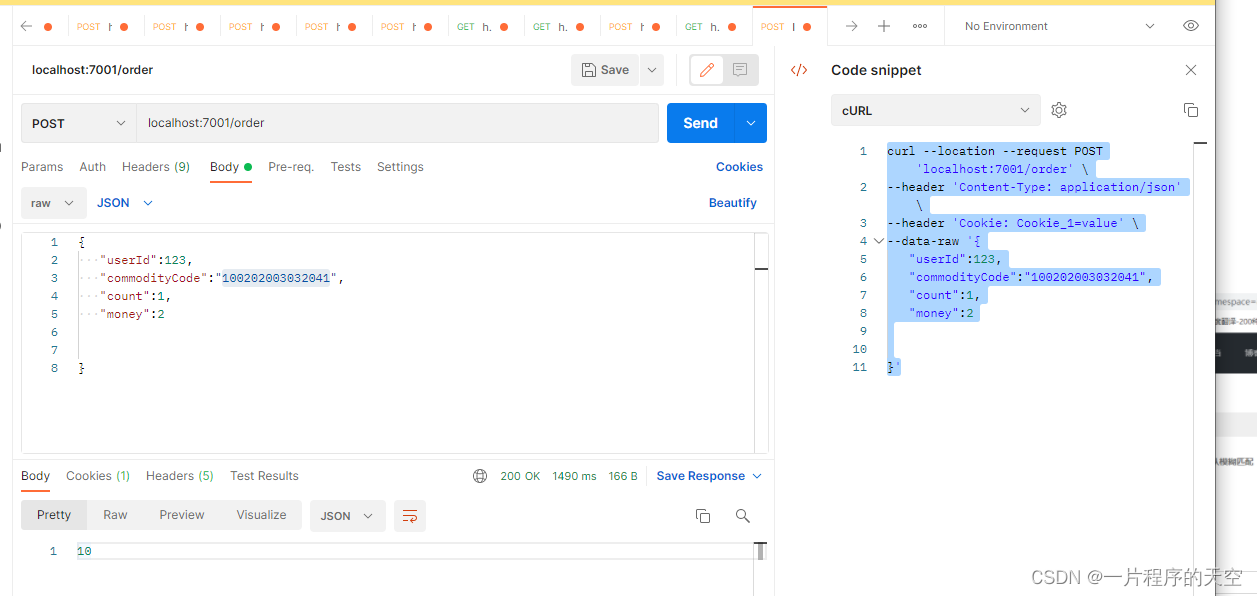
seata1.5.2使用从零快速上手(提供代码与安装包)
1.软件准备： 1.1 seata1.5.2 官网下载：地址:http://seata.io/zh-cn/ server源码:https://github.com/seata/seata 百度云下载（建议）: 百度下载 链接：https://pan.baidu.com/s/1eilbSI0YdmupHYI7FroTsw 提取码&…...
我的机器学习之路
名字比较大，就好比大麻袋，啥都可以往里装。 如果说人生就像旅行，那么通往不同风景必定是要由不同的路抵达的。 风景无穷尽，人生却有涯。 15年的时候也写过类似的一篇文章，可以叫做大数据之大路和机器学习的岔路。现在…...
react-swipeable-views轮播图实现下方的切换点控制组件
本文是react通过react-swipeable-views创建公共轮播图组件的续文 上一文 我们创建了这样的一个轮播图组件 但我们已经看到的轮播图 下面都会有小点 展示当前所在的位置 但react-swipeable-views 并没有直接提供 我们需要自己去编写这个组件 我们在components下的 rotationCh…...
假如你知道这样的JVM
一. Java 类加载过程？ Java 类加载需要经历一下 7 个过程： 加载 加载是类加载的第一个过程，在这个阶段，将完成一下三件事情： • 通过一个类的全限定名获取该类的二进制流。 • 将该二进制流中的静态存储结构转化为方法…...
css实现圆环展示百分比，根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...
【人工智能】神经网络的优化器optimizer（二）：Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad（Adaptive Gradient Algorithm）是一种自适应学习率的优化算法，由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率，适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...
SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题（可多选） 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘：专注于发现数据中…...
dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块，用户不点击提交按钮，只要输入框失去焦点，就会提前提示验证码是否正确。 一，模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...
如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时，你可能需要保留重要的数据，例如通讯录。好在，将通讯录从 iPhone 转移到 Android 手机非常简单，你可以从本文中学习 6 种可靠的方法，确保随时保持连接，不错过任何信息。 第 1…...
C++.OpenGL （10/64）基础光照（Basic Lighting）
基础光照（Basic Lighting） 冯氏光照模型（Phong Lighting Model） #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...
ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作：ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等（ArcGIS出图图例8大技巧），那这次我们看看ArcGIS Pro如何更加快捷的操作。…...
Redis的发布订阅模式与专业的 MQ（如 Kafka, RabbitMQ）相比，优缺点是什么？适用于哪些场景？
Redis 的发布订阅（Pub/Sub）模式与专业的 MQ（Message Queue）如 Kafka、RabbitMQ 进行比较，核心的权衡点在于：简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...
蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V，是一个正整数，表示每 V V V 个普通金属 O O O 可以冶炼出 …...
管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...