【蓝桥杯】蓝桥杯算法复习(一)
😀大家好,我是白晨,一个不是很能熬夜😫,但是也想日更的人✈。如果喜欢这篇文章,点个赞👍,关注一下👀白晨吧!你的支持就是我最大的动力!💪💪💪

文章目录
- 前言
- 蓝桥杯复习(一)
- 一、二分
- 复习
- 练习
- 二、前缀和
- 复习
- 练习
- 三、差分
- 复习
- 练习
- 四、双指针
- 复习
- 练习
- 五、归并
- 复习
- 练习
- 六、多路归并
- 复习
- 练习
- 七、贡献法
- 复习
- 练习
前言
本文适合有一定算法基础,但是由于各种原因已经很久没有敲代码的同学。本文以复习+练习为主,旨在通过练习算法题快速复习已经遗忘的算法。即使不是参加蓝桥杯的同学,如果符合上面的条件,依然可以参考本文进行复习。
如果你是新手,可以参考白晨的算法专栏进行学习。
蓝桥杯复习(一)
一、二分
复习
// 模板一
// 求满足check条件的最左下标
#include <iostream>using namespace std;template<class T>
int binary_search1(T* v, int l, int r)
{while (l < r){int mid = l + r >> 1;if (check(v[mid])) // check中 v[mid] 永远放在前面,eg. v[mid] >= ar = mid;elsel = mid + 1;}return mid;
}// 模板二
// 求满足check条件的最右下标
#include <iostream>using namespace std;template<class T>
int binary_search1(T* v, int l, int r)
{while (l < r){int mid = l + r + 1 >> 1; // 必须加一,避免死循环if (check(v[mid])) // eg.v[mid] <= al = mid;elser = mid - 1;}return mid;
}
练习

🍬题目链接:借教室
🍎算法思想:
由于题目中给出了n为 1 0 6 10^6 106,也即百万级别,所以应该使用时间复杂度为O(n)或者O(mlogn)(m较小),所以就不能直接模拟。
此题使用了差分和二分的思想,差分这里简单提一下:
一维差分数组是一种处理区间修改和查询的方法,它可以在O(1)的时间内实现对原数组某个区间内所有元素加上一个常数。具体来说,如果原数组是a[],差分数组是b[],那么有以下关系:
a[i] = b[1] + b[2] + … + b[i]b[i] = a[i] - a[i-1]
详细差分算法的介绍可见:【算法】算法基础入门详解
本题目订单为先来后到,并且订单都是正整数,所以每分配一个订单的教室,剩余的教室会越来越少,订单1到订单m具有单调性。所以将其转化为查找最多可以满足多少订单,这样就可以使用二分查找来确定能够处理的最大订单数量。在二分查找的过程中,将订单数量的上下界初始化为 0 和 m,然后在每次迭代中计算中间值 mid,并通过 check 函数来判断是否能够处理 mid 个订单。
要注意二分的模板分为两个,我们这次求得是满足check的最右下标,所以使用模板二。
🍊具体实现:
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;typedef long long LL;const int N = 1000010;int n, m;
int w[N];
int d[N], s[N], t[N];
LL b[N];bool check(int mid)
{memset(b, 0, sizeof b);// 先差分,求出分配前mid订单后的差分数组for (int i = 1; i <= mid; ++i) {b[s[i]] += d[i];b[t[i] + 1] -= d[i];}// 判断此时是否满足条件LL cnt = 0;for (int i = 1; i <= n; ++i) {cnt += b[i];if (cnt > w[i]) return false;}return true;
}int main()
{scanf("%d%d", &n, &m);for (int i = 1; i <= n; i ++ ) scanf("%d", &w[i]);for (int i = 1; i <= m; i ++ ) scanf("%d%d%d", &d[i], &s[i], &t[i]);// 求满足最多订单的订单编号int l = 0, r = m;while (l < r) {int mid = l + r + 1 >> 1;if (check(mid)) l = mid;else r = mid - 1;}if (r == m) printf("0");else printf("-1\n%d", r + 1);return 0;
}
二、前缀和
复习
前缀和是指:
如果有一个数组
s[N],那么其前缀和数组a[N]的定义为
a [ i ] = s [ 1 ] + s [ 2 ] + s [ 3 ] + . . . + s [ i ] a[i] = s[1]+s[2]+s[3]+...+s[i] a[i]=s[1]+s[2]+s[3]+...+s[i]
也即,前缀和就是数组s前i个数的总和,前缀和数组就是数组s前i个数的总和组成的数组。
有了这个数组,就可以以O(1)的时间复杂度算出s[l]~s[r]这段区间的总和:
s u m ( s [ l : r ] ) = a [ r ] − a [ l − 1 ] = s [ 1 ] + . . . + s [ l − 1 ] + s [ l ] + . . . + s [ r ] − s [ 1 ] − . . . s [ l − 1 ] = s [ l ] + . . . + s [ r ] sum(s[l:r])=a[r]-a[l-1]\\=s[1]+...+s[l-1]+s[l]+...+s[r]-s[1]-...s[l-1]\\=s[l]+...+s[r] sum(s[l:r])=a[r]−a[l−1]=s[1]+...+s[l−1]+s[l]+...+s[r]−s[1]−...s[l−1]=s[l]+...+s[r]
练习

🍬题目链接:壁画
🍎算法思想:
这个题的要点是被毁掉的墙段一定只与一段还未被毁掉的墙面相邻,所以被毁掉的墙壁一定是边缘的,不能是中间的,如果是中间的,就与两段未毁掉的墙壁相邻了。
理解了这个以后,还有几个点比较重要:
- 每天是先绘画,后毁坏,所以绘画的墙最后一定大于或等于被毁掉的墙;
- 绘画的墙一定是连续的,这就给使用前缀和创造了条件。
所以绘画的墙壁数量为 ⌈ n 2 ⌉ \lceil \frac{n}{2} \rceil ⌈2n⌉,现在如果证明出所有 ⌈ n 2 ⌉ \lceil \frac{n}{2} \rceil ⌈2n⌉的连续墙壁都可以取到就可。
现在,假设我们有长度为 n n n 的连续墙壁,考虑以下两种情况:
- 如果 n n n 是偶数,那么 ⌈ n 2 ⌉ = n 2 \lceil \frac{n}{2} \rceil = \frac{n}{2} ⌈2n⌉=2n。在这种情况下,由于人有先手优势,第一个可以涂你选定的那一段中间两个随便一个,接下来,如果墙从左边被毁下一次就涂上一次刚才涂画的左边的墙进行涂画,反之右边被毁就选上一次刚才涂画的右边的墙进行涂画,就是按照对称的方式走,这样走结果必然可以将选定的一段涂完。
- 如果 n n n 是奇数,那么 ⌈ n 2 ⌉ = n + 1 2 \lceil \frac{n}{2} \rceil = \frac{n+1}{2} ⌈2n⌉=2n+1。在这种情况下,先涂选定的一段中间的墙,后面同上,如果墙从左边被毁下一次就涂上一次刚才涂画的左边的墙进行涂画,反之右边被毁就选上一次刚才涂画的右边的墙进行涂画,也可以保证一定能涂完。
因此,无论 n n n 是偶数还是奇数,我们都可以选择任意一段 ⌈ n 2 ⌉ \lceil \frac{n}{2} \rceil ⌈2n⌉ 个连续的墙壁进行涂色,所以问题转化为了求一段固定长度的连续区间的最大值,这里使用滑动窗口也可以做,但是今天复习的是前缀和,就拿前缀和做就可以了。
🍊具体实现:
#include <iostream>
#include <cstring>
#include <algorithm>const int N = 5000010;int t, n;
char s[N];
int a[N];int main()
{scanf("%d", &t); // 输入测试用例数量for (int i = 1; i <= t; ++i){scanf("%d", &n); // 输入字符串长度scanf("%s", s + 1); // 输入字符串int res = 0;int cnt = (n + 1) / 2; // 滑动窗口的大小,取n的一半向上取整for (int j = 1; j <= n; ++j) {a[j] = a[j - 1] + s[j] - '0'; // 计算前缀和,即当前位置之前的数字和if (j >= cnt) res = std::max(res, a[j] - a[j - cnt]); // 更新结果,保证滑动窗口内数字的和最大}printf("Case #%d: %d\n", i, res); // 输出结果}return 0;
}三、差分
复习
一维差分数组是一种处理区间修改和查询的方法,它可以在O(1)的时间内实现对原数组某个区间内所有元素加上一个常数。具体来说,如果原数组是a[],差分数组是b[],那么有以下关系:
a[i] = b[1] + b[2] + … + b[i]b[i] = a[i] - a[i-1]
详细差分算法的介绍可见:【算法】算法基础入门详解
练习

🍬题目链接:空调
🍎算法思想:
针对每个位置,计算初始温度和目标温度之间的差值 a,然后利用 insert 函数将这个差值插入到差分数组 b 中。这个函数用来更新差分数组,以便跟踪累积的变化。
据题意,将一段区间升高或者降低1度在差分数组中就是将一个位置的数+1,另一个位置的数-1(这里注意如果到总区间最后一个也要改变,则可以理解为将其中一个位置+1或-1即可)。
所以,要将差分数组变为全0,也就是要将差分数组中全部正数和负数都通过-1和+1的操作变为0。最小的操作次数为 正数之和 和 负数之和的绝对值 中的最大值。
🍊具体实现:
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 100010;int n;
int p[N], t[N];
int b[N];void insert(int e, int l, int r)
{b[l] += e;b[r + 1] -= e;
}int main()
{scanf("%d", &n);for (int i = 1; i <= n; i++) scanf("%d", &p[i]);for (int i = 1; i <= n; i++) scanf("%d", &t[i]);for (int i = 1; i <= n; i++) {// 求温差int a = p[i] - t[i];insert(a, i, i);}int pos = 0, neg = 0;for (int i = 1; i <= n; ++i) {if (b[i] > 0) pos += b[i];else neg -= b[i];}printf("%d", max(pos, neg));return 0;
}
四、双指针
复习
练习

🍬题目链接:牛的学术圈 I
🍎算法思想:
依题意,h满足两个条件:
-
引用次数最小为
h - 1 -
值为h - 1的文章数 <= L
所以,最好先将文章的引用次数从大到小排序,i代表h的枚举,j代表从右到左第一个大于等于i的数的下标,第一个条件非常好判断,只用每次枚举的时候判断第i个数是否大于等于i - 1,第二个条件可以在输入的时候就用哈希表统计出每个数出现的次数,也可以使用双指针判断。
本次使用双指针判断,j代表从右到左第一个大于等于i的数的下标,也即下标大于j的数都小于i,而i必须满足第一个条件,也即a[i] >= i - 1,所以当a[i] = i - 1时i - j的数就是值为i - 1的数的个数。
🍊具体实现:
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 100010;int n, L;
int a[N];int main()
{scanf("%d%d", &n, &L);for (int i = 1; i <= n; i++) scanf("%d", &a[i]);sort(a + 1, a + 1 + n, greater<int>()); // 从大到小排序int res = 0;for (int i = 1, j = n; i <= n; i++){while (j && a[j] < i) j--; // 找到从右到左第一个大于等于i的数的下标// 判断此时的i是否满足上面提到的两个条件if (a[i] >= i - 1 && i - j <= L) res = i;}printf("%d", res);return 0;
}
五、归并
复习
- 逆序对个数
🍬题目链接:逆序对的数量
// 逆序对个数#include <iostream>using namespace std;typedef long long ll;const int N = 100010;// 不开longlong见祖宗
int v[N], tmp[N];ll merge_sort(int v[], int l, int r)
{if (l >= r) return 0;int mid = l + r >> 1;ll res = merge_sort(v, l, mid) + merge_sort(v, mid + 1, r);int k = 0, i = l, j = mid + 1;while (i <= mid && j <= r){if (v[i] <= v[j])tmp[k++] = v[i++];else{tmp[k++] = v[j++];// 逆序对的个数res += mid - i + 1; // v[i,mid] 都可以与 v[j] 组成逆序对}}while (i <= mid) tmp[k++] = v[i++];while (j <= r) tmp[k++] = v[j++];// 往原数组中还原for (i = l, j = 0; i <= r; ++i, ++j){v[i] = tmp[j];}return res;
}int main()
{int n;cin >> n;for (int i = 0; i < n; ++i)cin >> v[i];cout << merge_sort(v, 0, n - 1) << endl;return 0;
}
练习

🍬题目链接:火柴排队
🍎算法思想:
首先,简化一下问题,一个升序的序列a[]和一个随机序列b[],怎么调整第二个序列的顺序才能让 ∑ ( a i − b i ) 2 \sum(a_i -b_i)^2 ∑(ai−bi)2最小,当然我们可以猜一下,当两个序列都是升序时, ∑ ( a i − b i ) 2 \sum(a_i -b_i)^2 ∑(ai−bi)2最小。
可以反证一下,当第二个序列不是升序时,必然存在 b i > b i + 1 b_i>b_{i+1} bi>bi+1,此时得到的值为 ( a i − b i ) 2 + ( a i + 1 − b i + 1 ) 2 (a_i-b_i)^2+(a_{i+1}-b_{i+1})^2 (ai−bi)2+(ai+1−bi+1)2,将其交换顺序可得, ( a i − b i + 1 ) 2 + ( a i + 1 − b i ) 2 (a_i-b_{i+1})^2+(a_{i+1}-b_{i})^2 (ai−bi+1)2+(ai+1−bi)2,两者相减得到 2 ∗ ( a i − a i + 1 ) ( b i + 1 − b i ) > 0 2*(a_i-a_{i+1})(b_{i+1}-b_{i})>0 2∗(ai−ai+1)(bi+1−bi)>0,所以交换后得到的值小,所以第二个序列必须为升序序列。
其次,一个升序的序列a[]和一个随机序列b[],最少要相邻交换多少次才能将b[]调整到升序?
b[]中逆序对的个数就是最少要相邻的次数。
因为相邻交换只会改变 b i , b i + 1 b_i,b_{i+1} bi,bi+1之间的位置关系,并不会影响到 b i , b i + 1 b_i,b_{i+1} bi,bi+1和其他数的位置关系,所以交换一次,要么就是逆序对的数量减一,要么就是逆序对的数加一(不存在相同的数)。所以,最小交换次数大于等于逆序对的个数。
在b[]中必然存在 b i > b i + 1 b_i>b_{i+1} bi>bi+1,也即相邻的逆序对,如果不满足,那么b[]就是升序的,所以每次交换必然可以交换一对逆序对。这样就可以得到,最小交换次数等于逆序对的个数。
最后,回到原问题,如果是a[]不是升序序列,那么应该怎么办?
我们可以对a[]做一个映射,将其映射为升序序列,再以对a[]做的映射为规则,对b[]做映射,只用求出b[]中的逆序对数量,就是最小的交换次数。
但是,这里有一个问题,a[]和b[]的数不相同呀,怎么进行映射?由于本题目并不涉及数组中的具体值,只涉及到数组间的相对大小(逆序对),所以可以将其进行离散化,按照其数组中的相对大小将其离散化到1~10000上,这样就可以保证a[]和b[]可以相互映射。
🍊具体实现:
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 100010, mod = 99999997;int n;
int a[N], b[N];
int q[N], map[N];int merge_sort(int l, int r)
{if (l >= r) return 0;int mid = l + r >> 1;int res = (merge_sort(l, mid) + merge_sort(mid + 1, r)) % mod;int i = l, j = mid + 1, k = 0;while (i <= mid && j <= r) {// 统计逆序对个数if (b[i] > b[j]) q[k++] = b[j++], res = (res + mid - i + 1) % mod;else q[k++] = b[i++];}while (i <= mid) q[k++] = b[i++];while (j <= r) q[k++] = b[j++];for (i = l, j = 0; i <= r; ++i, ++j) b[i] = q[j];return res;
}void handler(int t[])
{for (int i = 1; i <= n; ++i) q[i] = i;// 按照数组数据大小排下标,排到前面的是小数的下标sort(q + 1, q + n + 1, [&](int x, int y){return t[x] < t[y];});for (int i = 1; i <= n; ++i) t[q[i]] = i;
}int main()
{scanf("%d", &n);for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);for (int i = 1; i <= n; ++i) scanf("%d", &b[i]);// 离散化handler(a), handler(b);// 对a数组的数做映射,使其成为升序数组// 并按照此映射规则映射b数组for (int i = 1; i <= n; ++i) map[a[i]] = i;for (int i = 1; i <= n; ++i) b[i] = map[b[i]];// 现在只要求出b数组的逆序对数,就是最小交换次数printf("%d", merge_sort(1, n));return 0;
}
六、多路归并
复习
多路归并(Multiway Merge)是一种常用的排序算法,用于合并多个已经排序的序列。它通常被用作外部排序算法,特别是在处理大型数据集时。
在多路归并中,假设有 k 个已经排好序的序列,每个序列包含 n 个元素。该算法将这 k 个序列合并成一个排序好的序列。多路归并的基本思路是维护一个大小为 k 的堆,每次从堆中选择最小的元素输出,并从相应的序列中取出下一个元素放入堆中,直到所有序列中的元素都被输出。
多路归并的时间复杂度取决于输入序列的总长度以及序列的个数。如果输入序列的总长度为 N,序列的个数为 k,那么多路归并的时间复杂度为 O(N * log(k))。
练习
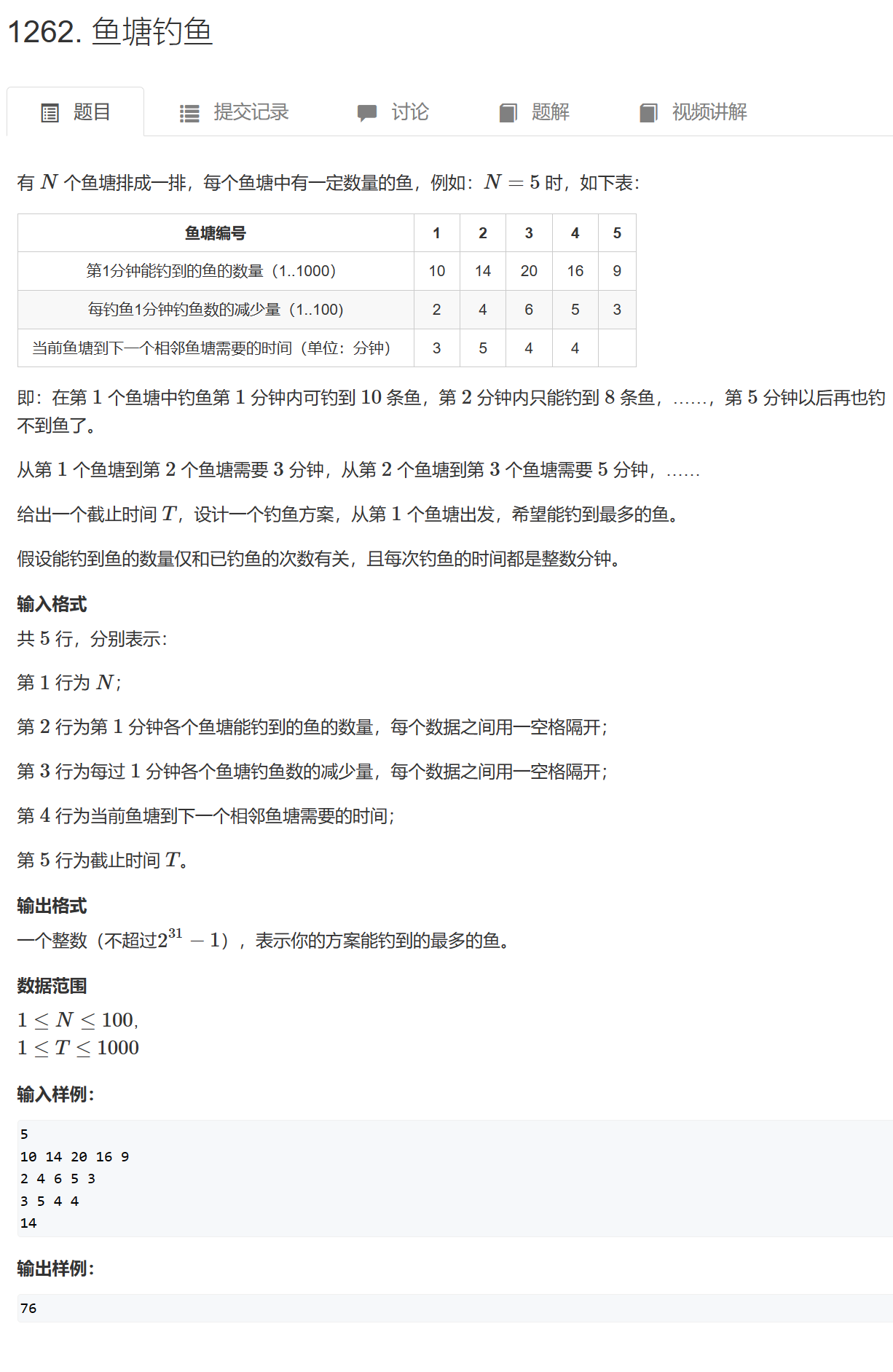
🍬题目链接:鱼塘钓鱼
🍎算法思想:
枚举+多路归并:
钓鱼真正的有效时间 = 总时间 - 在路上的时间,在路上的时间就是到第i个鱼池所用的时间,在一个鱼池钓到鱼的数量只与呆在这个鱼池的时间有关,而鱼池的鱼的数量不会随着时间进行恢复,所以可以在一个鱼池利益最大化以后再走,不需要回头。
可以枚举最远到达第i个鱼池,再求出在有效时间内,前i个鱼池最多可以钓多少鱼。由于每个鱼池每分钟可获得的鱼数只与在本鱼池呆的时间有关,所以在每个鱼池每分钟获得鱼的数量就是一个递减的序列,i个递减序列,要求有限时间内获得鱼的最大值,就直接使用多路归并的思想,从前i鱼池中每次选择获得鱼数最多的池子进行钓鱼,最后得到的就是在有效时间内,前i个鱼池最多可以钓到的鱼数。
🍊具体实现:
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 110;int n, t;
int a[N], d[N], w[N], s[N];// 求出此时第k个鱼池能获取的鱼数
int get(int k)
{return max(0, a[k] - d[k] * s[k]);
}int multi_merge(int k, int m)
{int res = 0;memset(s, 0, sizeof s);// 多路归并,求出前k个鱼池前m分钟的钓鱼的最大值for (int i = 1; i <= m; ++i) {int r = 1;// 直接循环求出最大值,如果是正规多路归并,应该使用堆,但是这里直接暴力循环也可以过for (int j = 2; j <= k; ++j) if (get(j) > get(r))r = j;res += get(r);s[r]++; //第r个鱼池呆的时长+1}return res;
}int main()
{scanf("%d", &n);for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);for (int i = 1; i <= n; ++i) scanf("%d", &d[i]);for (int i = 2; i <= n; ++i) {scanf("%d", &w[i]);w[i] += w[i - 1];}scanf("%d", &t);int res = 0;// 枚举最远到哪个鱼池for (int i = 1; i <= n; ++i) {// 求出前n个鱼池在t分钟内钓到最大鱼数// 钓鱼真正的有效时间 = t - 在路上的时间res = max(res, multi_merge(i, t - w[i]));}printf("%d", res);return 0;
}
七、贡献法
复习
贡献法就是计算每个元素对最终答案的贡献是多少,在枚举的过程中加起来。所以这类题目的关键是想到如何在枚举的过程中计算各个元素的贡献。
练习

🍬题目链接:孤独的照片
🍎算法思想:
贡献法+枚举+乘法原理:
枚举每一个字符为一段连续字符串中唯一的字符,如果我们能快速求出以此字符为唯一的字符串有多少个,就能快速求出要丢掉的照片有多少个。
统计每一个字符左右各有多少个连续的与自身不同字符的数量,例如
HGGGH
下标从1开始s[5]='H',其左边有3个连续的G,l[5]=3,右边没有字符,r[5]=0
s[3]='G',左边为G,没有连续的H,所以l[3]=0,同理r[3]=0
有了这些数据以后,
以 s [ i ] 为唯一的字符串数量 = l [ i ] ∗ r [ i ] + m a x ( l [ i ] − 1 , 0 ) + m a x ( r [ i ] − 1 , 0 ) 以s[i]为唯一的字符串数量 = l[i]*r[i]+max(l[i]-1,0)+max(r[i]-1,0) 以s[i]为唯一的字符串数量=l[i]∗r[i]+max(l[i]−1,0)+max(r[i]−1,0)
也即左边连续的串和右边连续的串排列组合,可以拼成的串的数量,左(1…n)和右(1…n)组合以及只有左或者只有右。
🍊具体实现:
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 500010;typedef long long LL;int n;
char s[N];
// 统计s[i]左右各有多少个连续与s[i]不同的字符
int l[N], r[N];int main()
{scanf("%d", &n);scanf("%s", s + 1);// 从左统计s[i]的左侧有多少连续的与s[i]不同的字符,eg. HGGGH l[2]=1,l[5]=3 for (int i = 1, h = 0, g = 0; i <= n; ++i)if (s[i] == 'G') l[i] = h, h = 0, g++;else l[i] = g, g = 0, h++;// 从右统计s[i]的右侧有多少连续的与s[i]不同的字符,eg. HGGGH r[1]=3,r[4]=1 for (int i = n, h = 0, g = 0; i >= 1; --i)if (s[i] == 'G') r[i] = h, h = 0, g++;else r[i] = g, g = 0, h++;LL res = 0;for (int i = 1; i <= n; ++i) res += (LL)l[i] * r[i] + max(l[i] - 1, 0) + max(r[i] - 1, 0);printf("%lld", res);return 0;
}
相关文章:

【蓝桥杯】蓝桥杯算法复习(一)
😀大家好,我是白晨,一个不是很能熬夜😫,但是也想日更的人✈。如果喜欢这篇文章,点个赞👍,关注一下👀白晨吧!你的支持就是我最大的动力!Ǵ…...

移动端精准测试简介
在测试领域每隔一段时间,就会有一些主流的测试技术,比如说:接口自动化,WebUI, AppUI自动化,然后就是测试平台的开发,各类专项测试(性能,安全),再到前几年的手机集群云测平…...

CCProxy代理服务器地址的设置步骤
目录 前言 一、下载和安装CCProxy 二、启动CCProxy并设置代理服务器地址 三、验证代理服务器设置是否生效 四、使用CCProxy进行代理设置的代码示例 总结 前言 CCProxy是一款常用的代理服务器软件,可以帮助用户实现网络共享和上网代理。本文将详细介绍CCProxy…...
)
探秘分布式神器RMI:原理、应用与前景分析(二)
本系列文章简介: 本系列文章将深入探究RMI远程调用的原理、应用及未来的发展趋势。首先,我们会详细介绍RMI的工作原理和基本流程,解析其在分布式系统中的核心技术。随后,我们将探讨RMI在各个领域的应用,包括分布式计算…...

[项目设计] 从零实现的高并发内存池(三)
🌈 博客个人主页:Chris在Coding 🎥 本文所属专栏:[高并发内存池] ❤️ 前置学习专栏:[Linux学习] ⏰ 我们仍在旅途 目录 4.CentralCache实现 4.1 CentralCache整体架构 4.2 围绕Span的相关设计…...

将Q算法和D算法结合应用到llm解码上之人在回路
将Q算法和D算法结合应用到llm解码上之人在回路 参考地址代码解释 参考地址 https://dongfangyou.blog.csdn.net/article/details/136466609 代码 import numpy as np from tqdm import tqdmfrom sample import net, char2id_dict, get_real_p# 假设的词汇表 VOCABULARY lis…...
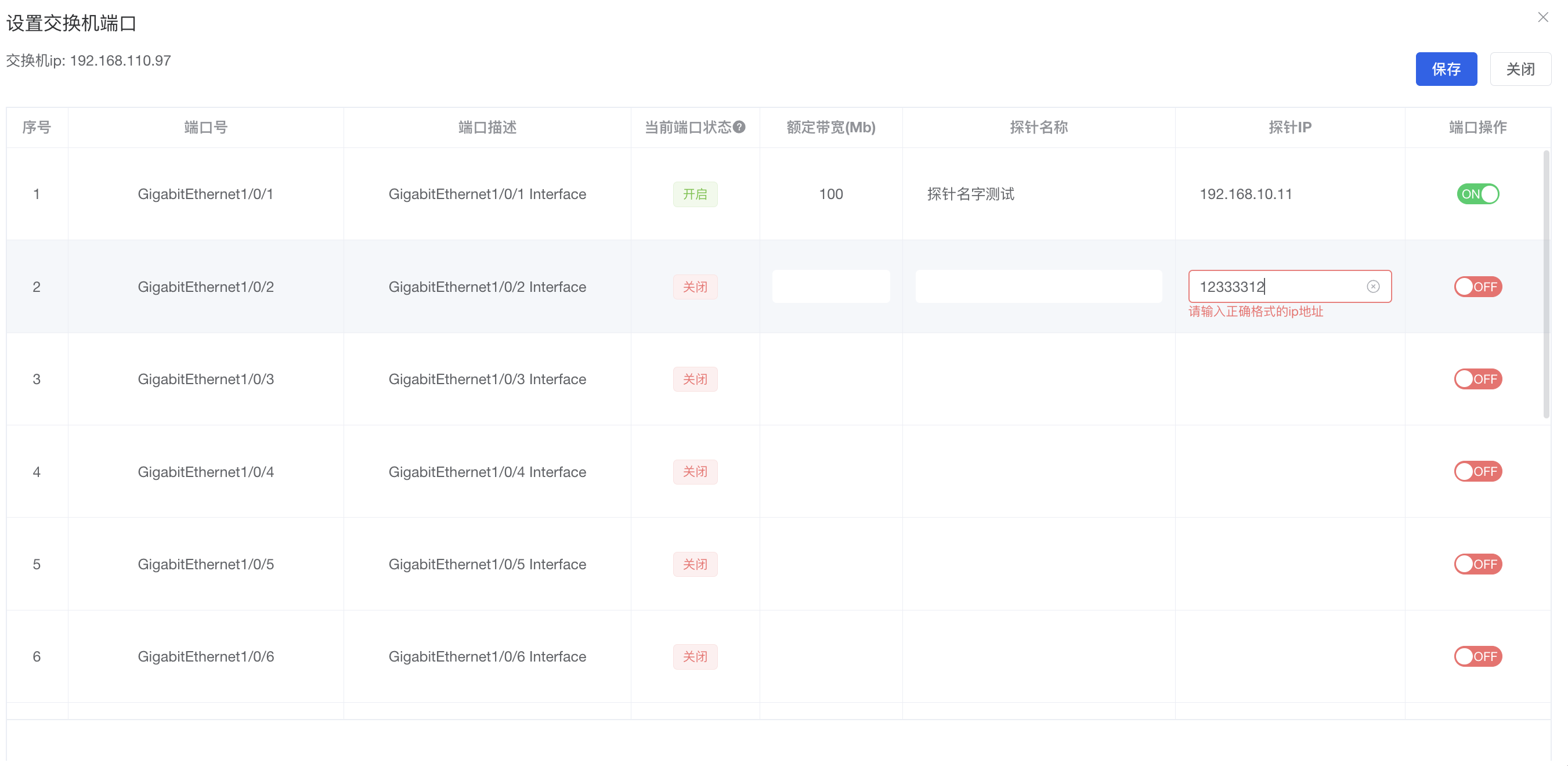
el-table-column嵌套el-form-item不能进行校验问题解决
项目为vue3elementPlus开发的项目 业务要求:table表格展示数据,其中有一行是ip地址可展示可修改,此处要求增加自定义校验规则 先看一下效果: 此处先描述一下,问题出在了哪里,我将el-table的data,使用一个…...

leetcode200. 岛屿数量
leetcode200. 岛屿数量 题目 思路 遍历每一个网格,若网格为1,岛屿数量1,利用一个深度优先搜索函数将岛屿置零,注意判断数组边界 代码 class Solution:def numIslands(self, grid: List[List[str]]) -> int:self.grid grid…...

MySQL--索引类型详解
索引的类型 主键索引: PRIMARY KEY,当一张表的某个列是主键的时候,该列就是主键索引,一张表只允许有一个主键索引,主键所在的列不能为空。 创建主键索引的SQL语法: # 给user表中的id字段创建名为id_ind…...

R语言中ggplot2图例位置、颜色、背景、标题
目录 1、不显示图例 2、自定义图例位置 3、修改图例背景颜色、外框颜色、大小 4、修改图例大小 5、图例设置背景、线框为空 6、自定义设置多个图例的标题 7、设置多个图例的之间的间隔 8、取消不需要的图例显示 1、不显示图例 theme(legend.position "none"…...

波卡 Alpha 计划启动,呼唤先锋创新者重新定义 Web3 开发
原文:https://polkadot.network/blog/the-polkadot-alpha-program-a-new-era-for-decentralized-building-collaboration/ 编译:OneBlock 区块链领域不断发展,随之而来的是发展和创新机会的增加。而最新里程碑是令人振奋的 Polkadot Alpha …...

公网IP与私有IP及远程互联
1.公网有私有IP及NAT 公网IP是全球唯一的IP,通过公网IP,接入互联网的设备是可以访问你的设备。但是IPV4资源有限,一般ISP(Internet Service Provider)并不会为用户提供公网IP。所以家里的计算机在公司是没法直接使用windows远程桌面直接访问…...

openCV xmake debug失效 release可以使用
在使用xmake构建一个项目时,添加openCV库,调用 imread函数时,debug函数失效, release可以使用,最后发现是xmake.lua写的有问题 option("OpenCV4.6.0")set_showmenu(true) set_default(true) set_category(&…...
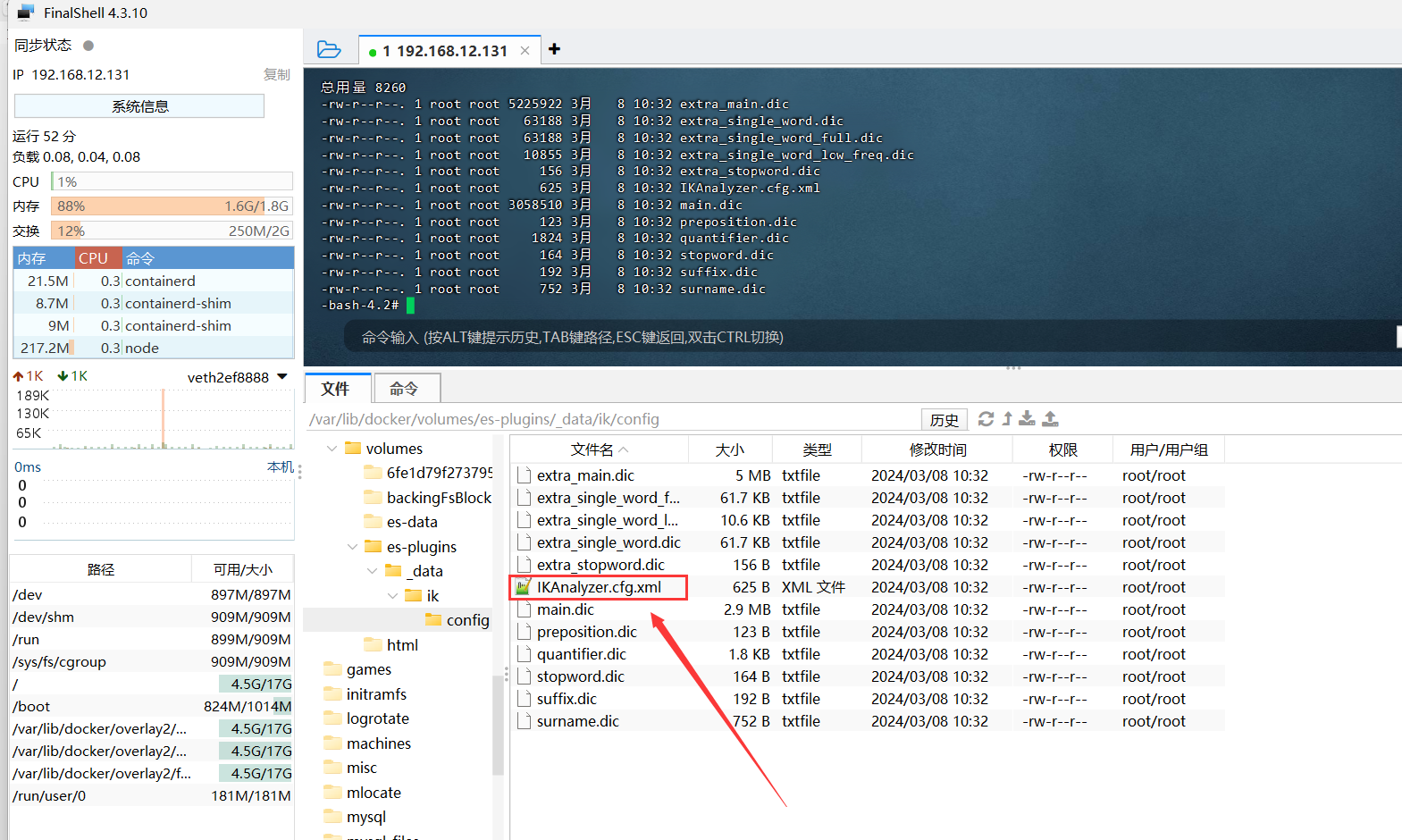
ES分布式搜索-IK分词器
ES分词器-IK 1、为什么使用分词器? es在创建倒排索引时需要对文档分词;在搜索时,需要对用户输入内容分词。但默认的分词规则对中文处理并不友好。 我们在kibana的DevTools中测试: GET /_analyze {"analyzer": "…...

基于卷积神经网络的野外可食用植物分类系统
温馨提示:文末有 CSDN 平台官方提供的学长 QQ 名片 :) 1. 项目简介 本文详细探讨了一基于深度学习的可食用植物图像识别系统。采用TensorFlow和Keras框架,利用卷积神经网络(CNN)进行模型训练和预测,并引入迁移学习模型…...
Raingad IM即时聊天/即时通讯网站源码,附带系统搭建教程
支持功能 支持单聊和群聊,支持发送表情、图片、语音、视频和文件消息单聊支持消息已读未读的状态显示,在线状态显示群聊创建、删除和群成员管理、群公告、群禁言等支持置顶联系人,消息免打扰;支持设置新消息声音提醒,…...
)
for语句的实际应用(3)
3145:【例24.3】 奇数求和 时间限制: 1000 ms 内存限制: 65536 KB 提交数: 9847 通过数: 5442 【题目描述】 计算非负整数 m 到 n(包括 m 和 n)之间的所有奇数的和,其中,m 不大于 n,且 n 不大…...

c++ Windows获取软件安装列表信息
链接 #include <windows.h> #include <stdio.h> #include <iostream> #include <vector>using namespace std;#ifndef MSVCR #define _T #define _tcscpy strcpy #define _stprintf sprintf #define _tcscmp strcmp #endifclass SetupSoftInfo { publ…...

音视频学习笔记——c++多线程(一)
✊✊✊🌈大家好!本篇文章主要整理了部分多线程相关的内容重点😇。首先讲解了多进程和多线程并发的区别以及各自优缺点,之后讲解了Thead线程库的基本使用。 本专栏知识点是通过<零声教育>的音视频流媒体高级开发课程进行系统…...

消息队列常见问题
总的来讲,消息队列常见问题要么消息不能多,要么不能少,还有顺序性,以及积压处理的问题等。 1.消息不能多 也就是说,消息不能重复消费,随之带来的幂等性问题。 解决:一般结合业务场景…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...

SQL Server 触发器调用存储过程实现发送 HTTP 请求
文章目录 需求分析解决第 1 步:前置条件,启用 OLE 自动化方式 1:使用 SQL 实现启用 OLE 自动化方式 2:Sql Server 2005启动OLE自动化方式 3:Sql Server 2008启动OLE自动化第 2 步:创建存储过程第 3 步:创建触发器扩展 - 如何调试?第 1 步:登录 SQL Server 2008第 2 步…...

Vue3中的computer和watch
computed的写法 在页面中 <div>{{ calcNumber }}</div>script中 写法1 常用 import { computed, ref } from vue; let price ref(100);const priceAdd () > { //函数方法 price 1price.value ; }//计算属性 let calcNumber computed(() > {return ${p…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...

算法—栈系列
一:删除字符串中的所有相邻重复项 class Solution { public:string removeDuplicates(string s) {stack<char> st;for(int i 0; i < s.size(); i){char target s[i];if(!st.empty() && target st.top())st.pop();elsest.push(s[i]);}string ret…...

Linux操作系统共享Windows操作系统的文件
目录 一、共享文件 二、挂载 一、共享文件 点击虚拟机选项-设置 点击选项,设置文件夹共享为总是启用,点击添加,可添加需要共享的文件夹 查询是否共享成功 ls /mnt/hgfs 如果显示Download(这是我共享的文件夹)&…...
