C语言基础练习——Day03
目录
选择题
编程题
记负均正
旋转数组的最小数字
选择题
1、已知函数的原型是:int fun(char b[10], int *a);,设定义:char c[10];int d;,正确的调用语句是
- A fun(c,&d);
- B fun(c,d);
- C fun(&c,&d);
- D fun(&c,d);
答案:A
解析:
本题考察了函数在调用过程中,实际参数和形式参数的匹配关系,本题函数原型为int fun(char b[10], int *a);,第一个形参是数组形式的参数,第二个形参是指针类型的参数,故在调用时传递的实际参数也需要为数组和指针类型(地址),所以第一个参数传数组的数组名,即数组首元素地址,第二个参数传变量d的地址
2、(多选题)请问下列表达式哪些会被编译器禁止
int a = 248, b = 4;
int const *c = 21;
const int *d = &a;
int *const e = &b;
int const * const f = &a;- A *c = 32;
- B *d = 43
- C e=&a
- D f=0x321f
答案:ABCD
解析:
本题考察了用const修饰的指针类型,对于指针变量c,由于const修饰的是指针变量整体,即*c,而因为c并没有得到实际有效的地址,所以解引用c会导致野指针问题,并且因为被const修饰,所以不可以使用解引用操作符改变变量c指向的空间中的值,对于指针变量d,同样也是const修饰指针变量整体,但d得到了a变量的地址,故d当前指向a变量所在的空间,但是因为被const修饰,所以同样不可以使用解引用操作符通过指针变量d改变a空间中的内容,对于指针变量e,const直接修饰变量,而不是修饰指针变量整体,并且指针变量e得到了b的地址,故此时可以使用*e修改b所在空间的内容,但是不可以改变指针变量e所指向的空间,对于指针变量f来说,同时被const修饰指针变量整体和变量名,此时既不可以改变f指向的地址,也不可以通过*f改变指向的空间的值
3、以下程序的输出结果为
#include <stdio.h>
int i;
void prt()
{for (i = 5; i < 8; i++)printf("%c", '*');printf("\t");
}
int main()
{for (i = 5; i <= 8; i++)prt();return 0;
}- A
*** - B
*** *** *** *** - C
*** *** - D
* * *
答案:A
解析:
本题中的变量i为全局变量,作用域为整个文件中,生命周期为持续到程序结束,故main函数中的变量i改变时,prt函数中的i依旧会改变,所以总共就执行了三次打印
4、下面代码段的输出是
int main()
{int a=3; printf("%d\n",(a+=a-=a*a));return 0;
}- A -6
- B 12
- C 0
- D -12
答案:D
解析:
本题考察了运算符的优先顺序以及C语言赋值运算符的赋值顺序,对于表达式a+=a-=a*a来说,先计算a*a结果为9,但是这个计算没有副作用,所以a变量中的值还是3,再执行a-=,即a = a - 9,因为a中当前为3,故a此时为3-9=-6,接着执行a+=,因为a当前值为-6,所以a=(-6)+(-6),故a的值为-12
5、下列不能实现死循环的是( )
- A
while(1){} - B
for(;1;){} - C
do{}while(1); - D
for(;0;){}
答案:D
解析:
在C语言中,循环执行的条件时判断表达式部分为真,而只要该部分中的值不为0即为真,故只有循环D无法实现死循环
编程题
记负均正
题目链接:记负均正_牛客题霸_牛客网 (nowcoder.com)
描述
首先输入要输入的整数个数n,然后输入n个整数。输出为n个整数中负数的个数,和所有正整数的平均值,结果保留一位小数。
0即不是正整数,也不是负数,不计入计算。如果没有正数,则平均值为0。
数据范围:1≤ n ≤2000 ,输入的整数都满足 ∣val∣≤1000
输入描述:
首先输入一个正整数n,
然后输入n个整数。
输出描述:
输出负数的个数,和所有正整数的平均值。
思路解析:
本题处理好负数和0的个数即可,在最后求平均值的过程中需要考虑到除数为0的情况
参考代码:
#include <stdio.h>int main() {int num = 0;int sum = 0;int input = 0;int count = 0;//记录负数的个数int zero = 0;//记录0的个数scanf("%d", &num);for(int i = 0; i < num; i++){scanf("%d", &input);if(input > 0){sum += input;}else if(input < 0){count++;}else {zero++;}}//如果输入的数值中不全是负数和0时计算平均数,否则不计算平均数if(num != count && num != zero){printf("%d %.1f", count, (float)sum/(num - count - zero));}else {printf("%d %.1f", count, 0.0);}return 0;
}旋转数组的最小数字
题目链接:旋转数组的最小数字_牛客题霸_牛客网 (nowcoder.com)
描述
有一个长度为 n 的非降序数组,比如[1,2,3,4,5],将它进行旋转,即把一个数组最开始的若干个元素搬到数组的末尾,变成一个旋转数组,比如变成了[3,4,5,1,2],或者[4,5,1,2,3]这样的。请问,给定这样一个旋转数组,求数组中的最小值。
数据范围:1≤ n≤10000,数组中任意元素的值: 0≤ val≤10000
要求:空间复杂度: O(1) ,时间复杂度: O( logn)
思路分析:
因为原数组是一个非降序(即非严格递增)的数组,所以旋转后的数组将被分为两个有序的数组,对于二分查找来说,只需要查找的数组是有序即可,对于本题,因为存在两个有序的部分,故需要分别进行判断,确定好边界后缩小范围再进行二分查找,故本题有三种情况
范围内的中间数值比右侧范围中的数值大。此时说明,数组中的最小数值在中间值的右侧,此时运用二分查找算法的思想,在右侧的部分中找最小值
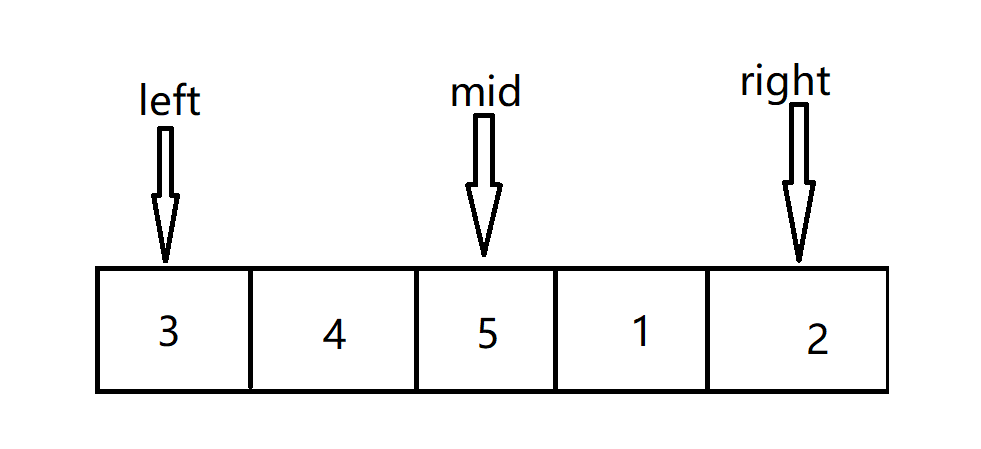
范围内的中间数值比右侧范围中的数值小。此时说明,数组中的最小数值在中间值的左侧,此时运用二分查找算法的思想,在左侧的部分中找最小值
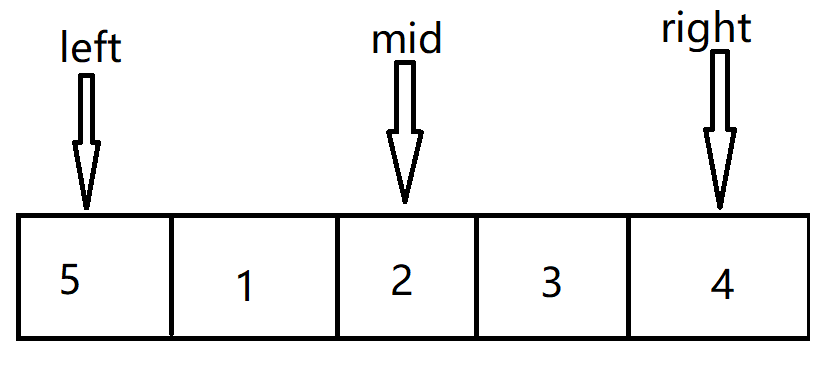
范围内的中间数值和右侧范围中的数值相等。此时无法判断数组中的最小数值在哪一侧,此时逐渐缩小区间,重复判断直到出现上面两种情况中的一种再执行上面的两种情况的处理方法

/*** 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可** * @param nums int整型一维数组 * @param numsLen int nums数组长度* @return int整型*/
int minNumberInRotateArray(int* nums, int numsLen )
{int left = 0;int right = numsLen - 1;while(left <= right){//指向中间位置的变量int mid = (left + right) / 2;if(nums[mid] > nums[right]){//当中间值大于右侧的值//注意此处是left = mid + 1,left用于和right确定边界,当需要缩小范围时,mid位置的数值可以不再包括在内,因为当前数值已经比nums[right]大left = mid + 1;}else if(nums[mid] < nums[right]){//当中间值小于右侧的值//注意此处不是right = mid - 1,因为要与nums[right]进行比较从而确定边界,可能mid位置就是一侧边界right = mid;}else {//当中间值等于右侧的值right--;}}return nums[left];
}相关文章:

C语言基础练习——Day03
目录 选择题 编程题 记负均正 旋转数组的最小数字 选择题 1、已知函数的原型是:int fun(char b[10], int *a);,设定义:char c[10];int d;,正确的调用语句是 A fun(c,&d);B fun(c,d);C fun(&c,&d);D fun(&c,d); 答…...

膜厚测量仪在半导体应用中及其重要
随着科技的不断发展,半导体行业已成为当今世界的核心产业之一。在这个领域中,半导体膜厚测量仪作为关键设备,其精度和可靠性对于产品质量和生产效率具有至关重要的作用。本文将详细介绍半导体膜厚测量仪的工作原理、应用领域以及其在半导体制…...

【前端】-初始前端以及html的学习
💖作者:小树苗渴望变成参天大树🎈 🎉作者宣言:认真写好每一篇博客💤 🎊作者gitee:gitee✨ 💞作者专栏:C语言,数据结构初阶,Linux,C 动态规划算法🎄 如 果 你 …...

uni-app navigateTo路由传参传递对象
传递参数 先通过JSON.stringify将对象转成字符串 toNextPage(obj) {uni.navigateTo({url:/pages/nextpage/index?obj${JSON.stringify(obj)}}); },接收参数 再通过JSON.parse将传递过来的字符串转成对象 onLoad(options) {this.obj JSON.parse(options.obj) }...

99 centos 7 服务器上面 增加了 2181 的防火墙配置, 但是客户端连接不上
呵呵 最近部署 zookeeper 的时候出现这样的一个问题 centos 7 服务器上面 增加了 2181 的防火墙配置, 但是客户端连接不上 # 但是再 另外的一个虚拟机环境, ubuntu 16 的环境, docker 启动 2181 的服务, 然后 安装 firewalld, 配置 开放 2181 的 tcp 服务, 客户端能够正常连接…...

云计算科学与工程实践指南--章节引言收集
云计算科学与工程实践指南–章节引言收集 //本文收集 【云计算科学与工程实践指南】 书中每一章节的引言。 我已厌倦了在一本书中阅读云的定义。难道你不失望吗?你正在阅读一个很好的故事,突然间作者必须停下来介绍云。谁在乎云是什么? 通…...

探索Web中的颜色选择:不同取色方法的实现
在Web开发中,提供用户选择颜色的功能是很常见的需求。无论是为了个性化UI主题,还是为了图像编辑工具,一个直观且易用的取色器都是必不可少的。本文将介绍几种在Web应用中实现取色功能的方法,从简单的HTML输入到利用现代API的高级技…...
)
突破编程_C++_设计模式(策略模式)
1 策略模式的概念 策略模式(Strategy Pattern)是 C 中常用的一种行为设计模式,它能在运行时改变对象的行为。在策略模式中,一个类的行为或其算法可以在运行时更改。这种类型的设计模式属于行为模式。 在策略模式中,需…...

【uniapp】uniapp小程序中实现拍照同时打开闪光灯的功能,拍照闪光灯实现
一、需求前提 特殊场景中,需要拍照的同时打开闪光灯,(例如黑暗场景下的设备维护巡检功能)。 起初我是用的uviewui中的u-upload组件自带的拍照功能,但是这个不支持拍照时打开闪光灯,也不支持从通知栏中打开…...

在python model train里如何驯服野生log?
关键词:python 、epoch、loss、log 🤖: 记录模型的训练过程的步骤如下: 导入logging模块。配置日志记录器,设置日志文件名、日志级别、日志格式等。在每个epoch结束时,使用logging模块记录性能指标、损失值、准确率等信…...

产品推荐 - Xilinx FPGA下载器 XQ-HS/STM2
1 FPGA下载器简介 1.性能优良 FPGA下载器XQ-HS/STM2采用Xilinx下载模块设计而成(JTAG-SMT2NC模块,该模块与Xilinx官方开发板KC705,KCU105,ZC702,ZC706,Zedboard等板载下载器一样,下载速度快…...

STM32 SDRAM知识点
1.SDRAM和SRAM的区别 SRAM不需要刷新电路即能保存它内部存储的数据。而SDRAM(Dynamic Random Access Memory)每隔一段时间,要刷新充电一次,否则内部的数据即会消失,因此SRAM具有较高的性能,但是SRAM也有它…...

手写分布式配置中心(六)整合springboot(自动刷新)
对于springboot配置自动刷新,原理也很简单,就是在启动过程中用一个BeanPostProcessor去收集需要自动刷新的字段,然后在springboot启动后开启轮询任务即可。 不过需要对之前的代码再次做修改,因为springboot的配置注入value("…...
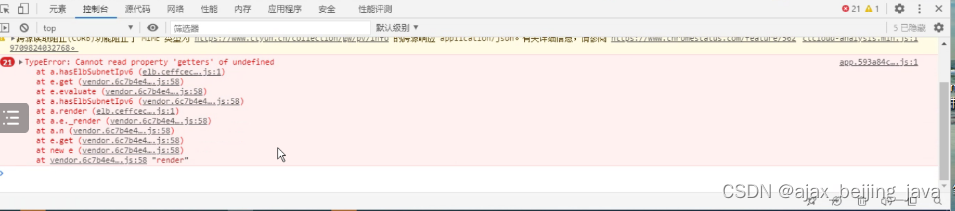
记录一次排查负载均衡不能创建的排查过程
故障现象,某云上,运维同事在创建负载均衡的时候,发现可以创建资源,但是创建完之后,不显示对应的负载均衡。 创建负载均衡时候,按f12发现console有如下报错 后来请后端网络同事排查日志发现,是后…...

数据推送解决方案调研
需求 文档编辑类型的需求,左侧是菜单栏,右侧是内容块,现在的需求时,如果多人同时编辑这个方案,当添加章节/调整章节顺序/删除章节时,其他用户能够及时感知到。 解决方案调研 前端轮询 最简单的方案&…...
)
二、NLP中的序列标注(分词、主体识别)
一般来说,一个序列指的是一个句子,而一个元素指的是句子中的一个词。在序列标注中,我们想对一个序列的每一个元素标注一个分类标签。比如信息提取问题可以认为是一个序列标注问题,如提取出会议时间、地点等。 常见的应用场景&…...
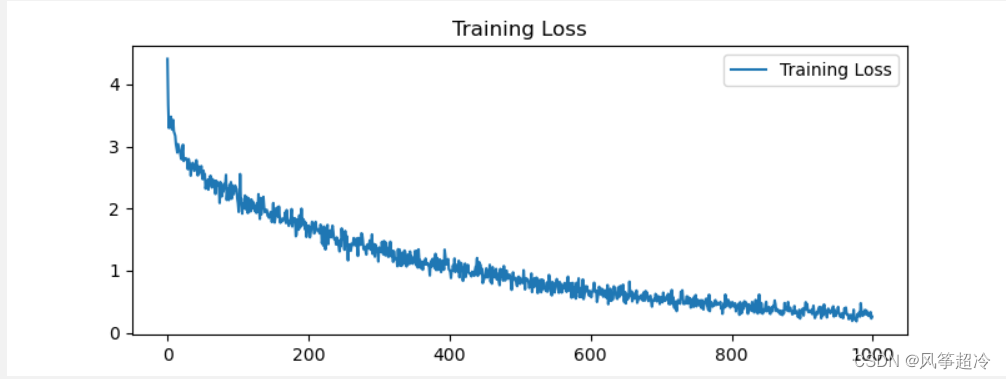
seq2seq翻译实战-Pytorch复现
🍨 本文为[🔗365天深度学习训练营学习记录博客 🍦 参考文章:365天深度学习训练营 🍖 原作者:[K同学啊 | 接辅导、项目定制]\n🚀 文章来源:[K同学的学习圈子](https://www.yuque.com/…...
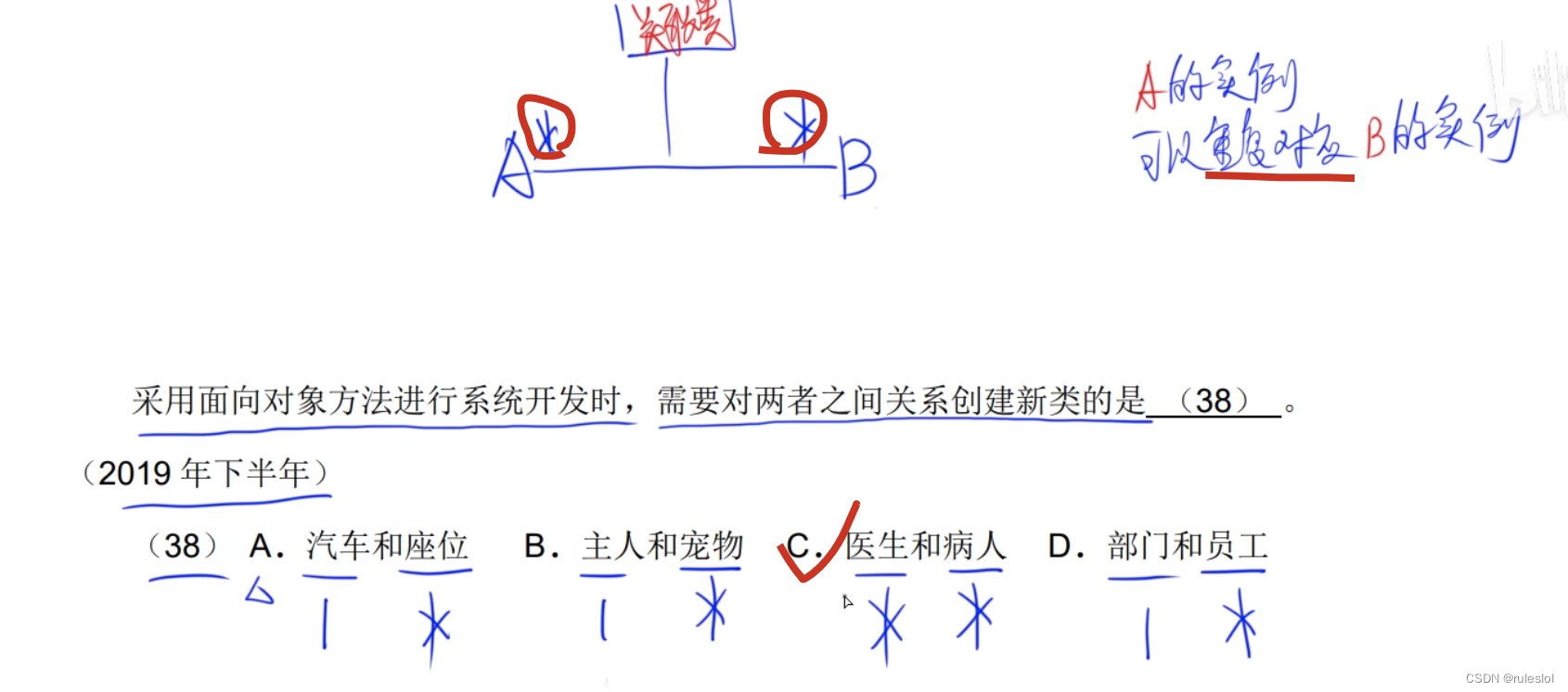
软考69-上午题-【面向对象技术2-UML】-关系
一、关系 UML中有4种关系: 依赖;关联;泛化;实现。 1-1、依赖 行为(参数),参数就是被依赖的事物,即:独立事物。 当独立事物发生变化时,依赖事务行为的语义也…...

智慧文旅|AI数字人导览:让旅游体验不再局限于传统
AI数字人导览作为一种创新的展示方式,已经逐渐成为了VR全景领域的一大亮点,不仅可以很好的嵌入在VR全景中,更是能够随时随地为观众提供一种声情并茂的讲解介绍,结合VR场景的沉浸式体验,让观众仿佛置身于真实场景之中&a…...

spring boot 集成 mysql ,mybatisplus多数据源
1、需要的依赖,版本自行控制 <dependency><groupId>com.alibaba</groupId><artifactId>druid</artifactId> </dependency><dependency><groupId>mysql</groupId><artifactId>mysql-connector-java<…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...
