数据结构——堆的应用 堆排序详解
💞💞 前言
hello hello~ ,这里是大耳朵土土垚~💖💖 ,欢迎大家点赞🥳🥳关注💥💥收藏🌹🌹🌹
💥个人主页:大耳朵土土垚的博客
💥 所属专栏:数据结构学习笔记
💥对于数据结构顺序表、链表、堆有疑问的都可以在上面数据结构的专栏进行学习哦~
有问题可以写在评论区或者私信我哦~
在土土的上篇博客二叉树堆的介绍与实现中,我们发现测试代码是升序;今天我们就来分析堆的重要应用——**堆排序**🎉🎉。
#include"Heap.h"
int main()
{Heap hp;HeapInit(&hp);int a[] = { 65,100,70,32,50,60 };for (int i = 0; i < 6; i++){HeapPush(&hp, a[i]);}while (!HeapEmpty(&hp)){int top = HeapTop(&hp);printf("%d\n", top);HeapPop(&hp);}HeapDestroy(&hp);return 0;
}
详情可在土土的博客数据结构——lesson7二叉树堆的介绍与实现中查看🥳🥳
一、堆排序(基础版)
既然是堆排序,那我们首先肯定得有一个堆,这里土土就可以偷个懒将上篇博客中实现的堆代码copy一下🥰🥰
堆的实现
#include"Heap.h"
//堆的初始化
void HeapInit(Heap* hp)
{assert(hp);hp->a = NULL;hp->capacity = 0;hp->size = 0;
}
// 堆的销毁
void HeapDestroy(Heap* hp)
{assert(hp);free(hp->a);hp->a = NULL;hp->capacity = 0;hp->size = 0;
}
//交换函数
void Swap(HPDataType* a,HPDataType* b)
{HPDataType tmp = *a;*a = *b;*b = tmp;
}//堆向下调整算法
void AdjustDown(HPDataType* a, int n,int parent)
{//找到较小的孩子节点int child = parent * 2 + 1;//向下调整while (child < n){if (child + 1 < n && a[child] > a[child + 1]){child++;}if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = child * 2 + 1;}elsebreak;}
}//向上调整
void AdjustUp(HPDataType* a,int child)
{//找到双亲节点int parent = (child - 1) / 2;//向上调整while (child > 0){if (a[parent] > a[child]){Swap(&a[parent], &a[child]);child = parent;parent = (child - 1) / 2;}elsebreak;}
}
// 堆的插入
void HeapPush(Heap* hp, HPDataType x)
{assert(hp);//判断容量if (hp->size == hp->capacity)//容量满了扩容{int newcapacity = hp->capacity == 0 ? 0 : 2 * hp->capacity;HPDataType* new = (HPDataType*)realloc(hp->a, sizeof(HPDataType) * newcapacity);if (new == NULL){perror("realloc fail");return;}hp->a = new;hp->capacity = newcapacity;}//尾插hp->a[hp->size] = x;hp->size++;//向上调整算法AdjustUp(hp->a,hp->size-1);
}
// 堆的删除,删除堆顶元素
void HeapPop(Heap* hp)
{assert(hp);assert(!HeapEmpty(hp));Swap(&hp->a[0], &hp->a[hp->size - 1]);hp->size--;//向下调整算法AdjustDown(hp->a, hp->size, 0);}
// 取堆顶的数据
HPDataType HeapTop(Heap* hp)
{assert(hp);assert(!HeapEmpty(hp));return hp->a[0];
}
// 堆的数据个数
int HeapSize(Heap* hp)
{assert(hp);return hp->size;}
// 堆的判空
int HeapEmpty(Heap* hp)
{assert(hp);return hp->size == 0;
}当然在使用这些函数时要记得先声明一下,这里我们都放到一个头文件Heap.h中
Heap.h
#pragma once
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
typedef int HPDataType;
//构建一个结构体封装堆
typedef struct Heap
{HPDataType* a;//数组顺序表int size;//堆元素个数int capacity;//数组空间
}Heap;
//以下是实现堆的函数
// 堆的初始化
void HeapInit(Heap* hp);
// 堆的销毁
void HeapDestroy(Heap* hp);
// 堆的插入
void HeapPush(Heap* hp, HPDataType x);
// 堆的删除
void HeapPop(Heap* hp);
// 取堆顶的数据
HPDataType HeapTop(Heap* hp);
// 堆的数据个数
int HeapSize(Heap* hp);
// 堆的判空
int HeapEmpty(Heap* hp);使用时只需包含该头文件即可
#include"Heap.h"
堆排序
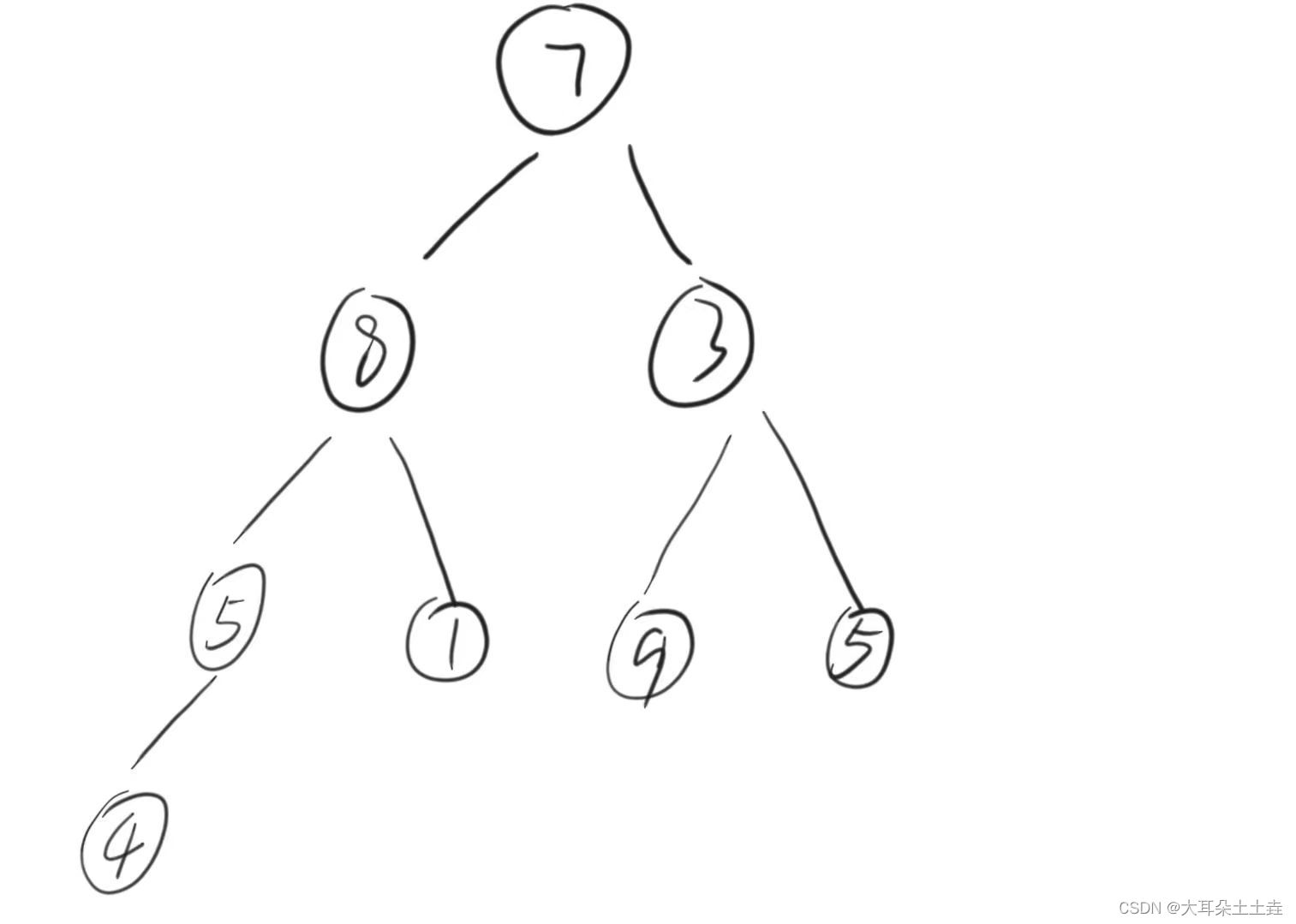
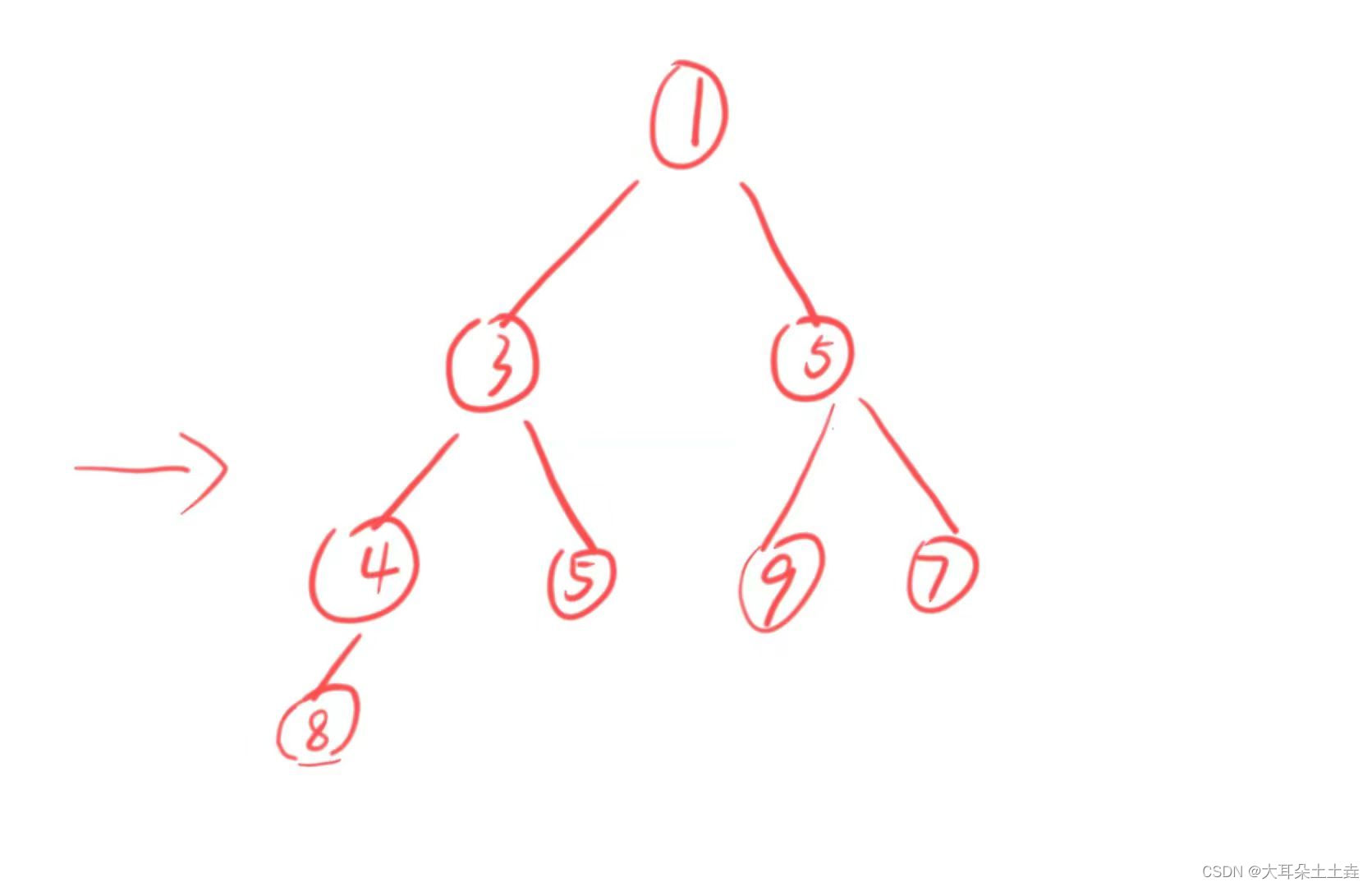
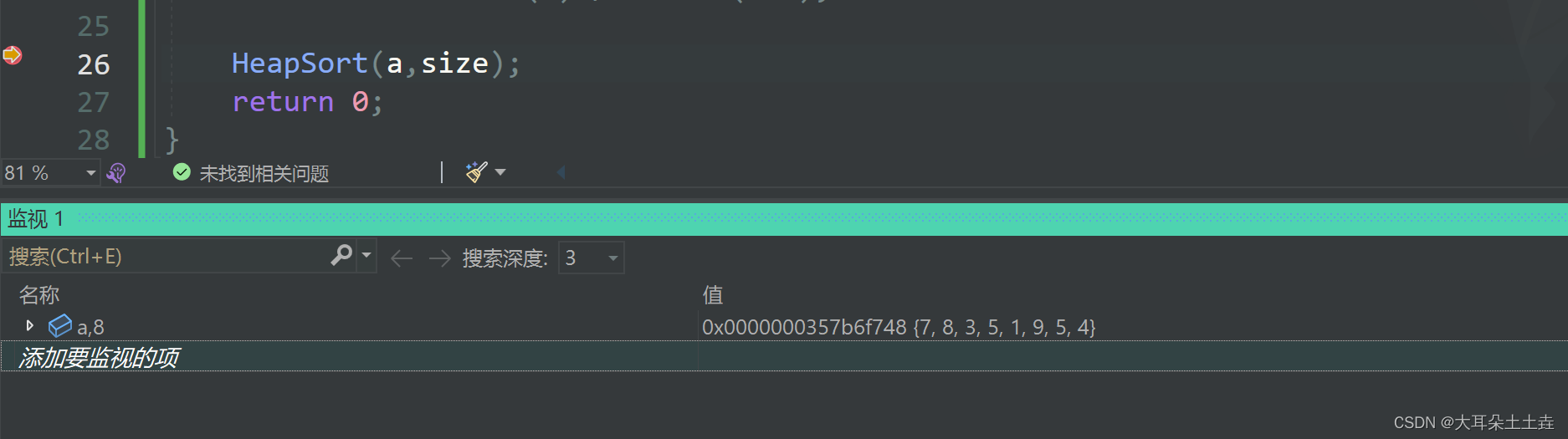
给定一个数组a[ ] = {7,8,3,5,1,9,5,4},我们需要利用上面的堆来将它进行排序
🤩🤩思路:
①我们首先需要将数组中的元素插入堆中(利用HeapPush函数),
💫前面我们已经学习过堆插入函数,它里面利用堆向上调整算法会自动将插入的数据调整为一个堆(我们实现的是小堆);
②然后我们需要获取堆顶元素(也就是小堆中最小的元素),利用HeapTop函数即可;
③获取最小元素后我们就需要获取次小元素,先利用堆的删除函数(HeapPop函数),将堆顶元素(也就是小堆中最小的元素)删除;
💞删除函数中堆向下调整算法又会将剩余元素调整为小堆,此时堆顶元素就是删除一个元素后最小的元素;
④将删除后的元素重新拷贝回数组a中;
⑤循环②③两步直到全部排序成功。
代码实现如下:
#include"Heap.h"
void HeapSort(int* a,int size)
{
Heap hp;
HeapInit(&hp);
//将a中元素插入堆中
for (int i = 0; i < size; i++)
{
HeapPush(&hp, a[i]);
}
//获取堆顶(最小)元素并删除
int i = 0;
while (i < size)
{
a[i++] = HeapTop(&hp);
HeapPop(&hp);
}
HeapDestroy(&hp);
}
int main()
{
int a[] = { 7,8,3,5,1,9,5,4 };
int size = sizeof(a) / sizeof(int);
HeapSort(a,size);
return 0;
}
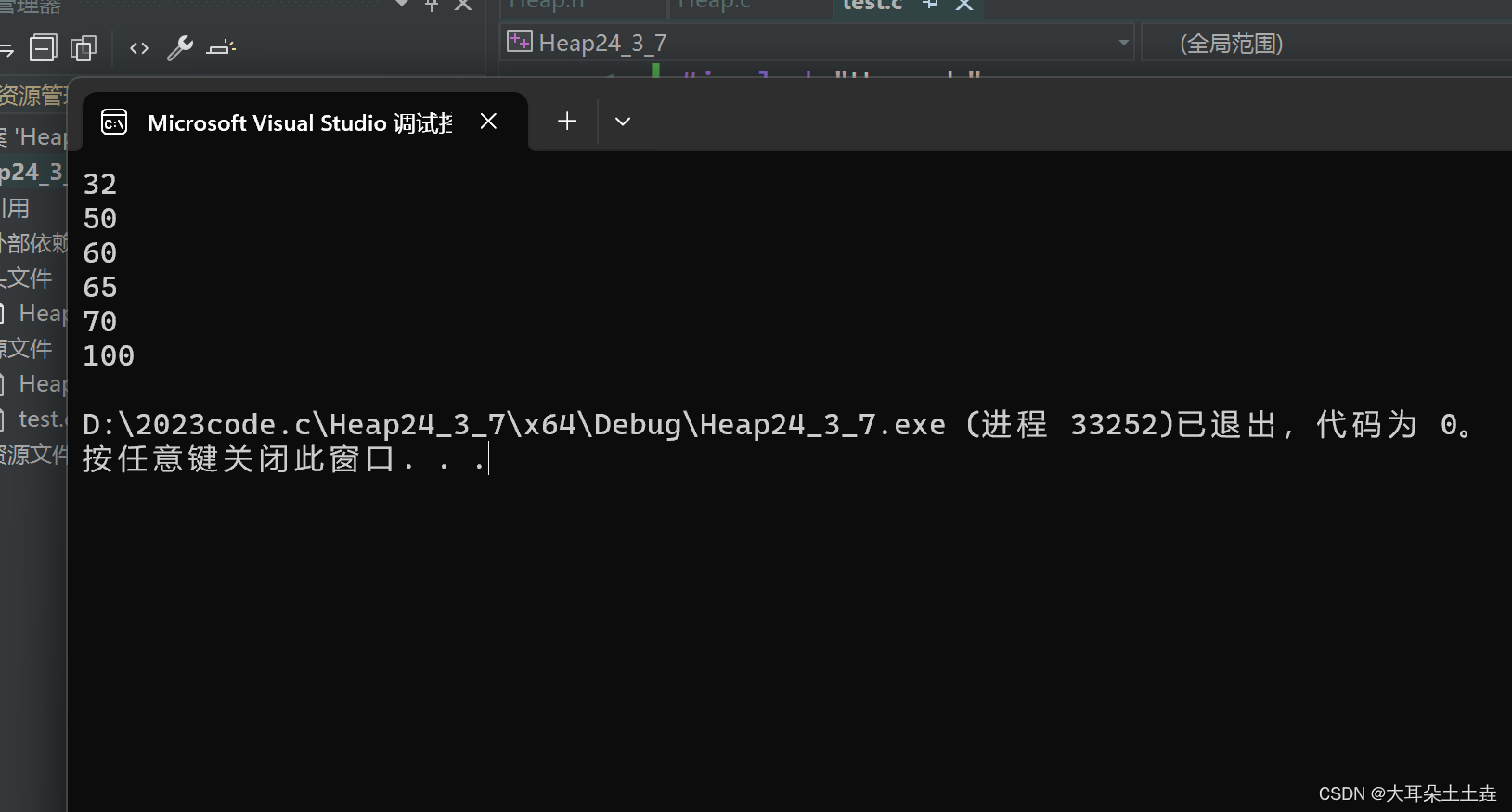
🥳🥳结果如下:
排序前:
排序后:
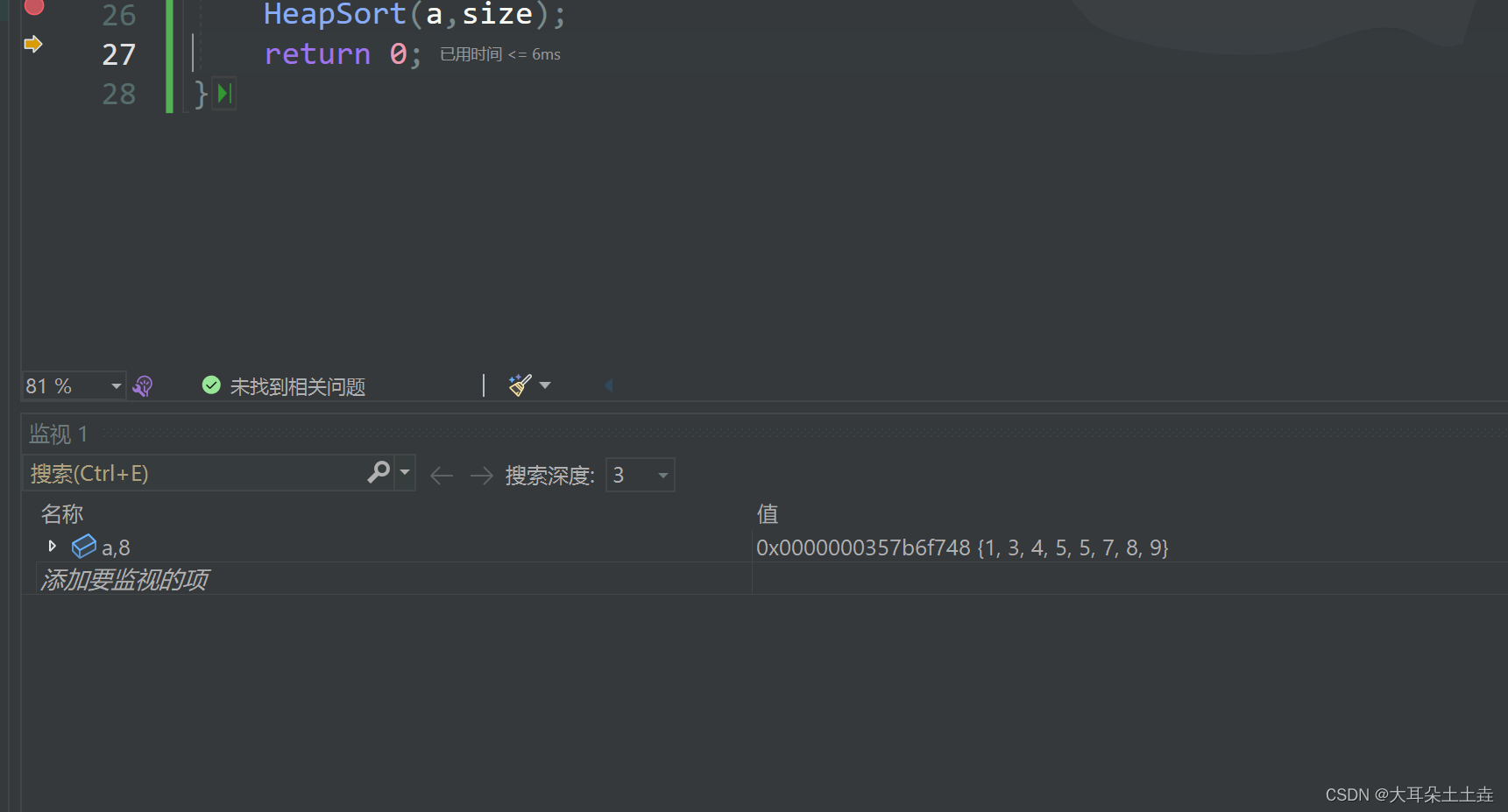
💥💥上述堆排序的实现尽管能够实现排序,但是…我们发现如果没有提前实现堆或者准备好堆的代码,我们是没办法实现的,而且我们需要来回拷贝数据,空间复杂度较大。
🥰🥰这里就需要介绍下面简便版堆排序啦~
二、堆排序(简便版)
在土土的数据结构学习笔记数据结构——lesson7二叉树堆的介绍与实现中,详细介绍了堆向上调整算法与堆向下调整算法,接下来我们就可以利用这两个函数来实现堆以及堆的排序🥳🥳
(1)利用堆向上调整算法实现堆
//向上调整算法
void AdjustUp(HPDataType* a,int child)
{//找到双亲节点int parent = (child - 1) / 2;//向上调整while (child > 0){if (a[parent] > a[child]){Swap(&a[parent], &a[child]);child = parent;parent = (child - 1) / 2;}elsebreak;}
}数组a[ ] = {7,8,3,5,1,9,5,4},我们可以看成一个二叉树:
只需要从第二个数8开始每次读取一个数据都向上调整为堆,那么读完整个数组就可以得到一个堆啦~🥰🥰
//从第二个数据开始向上调整建堆
for (int i = 1; i < size; i++)
{AdjustUp(a, i);
}
🤩🤩之前基础版排序是又开辟了一个空间来存放a中的数据,排成堆后又每次选取最小的元素拷贝回a中,不仅麻烦而且会增加空间的使用;
所以简便版排序便直接将a看成一个二叉树利用向上调整算法直接成堆,不需要开辟额外的空间。
(2)利用堆向下调整算法排序
那我们应该怎么将堆中的元素排序呢?
🥳🥳这就要利用堆向下调整算法了
思路🥳🥳
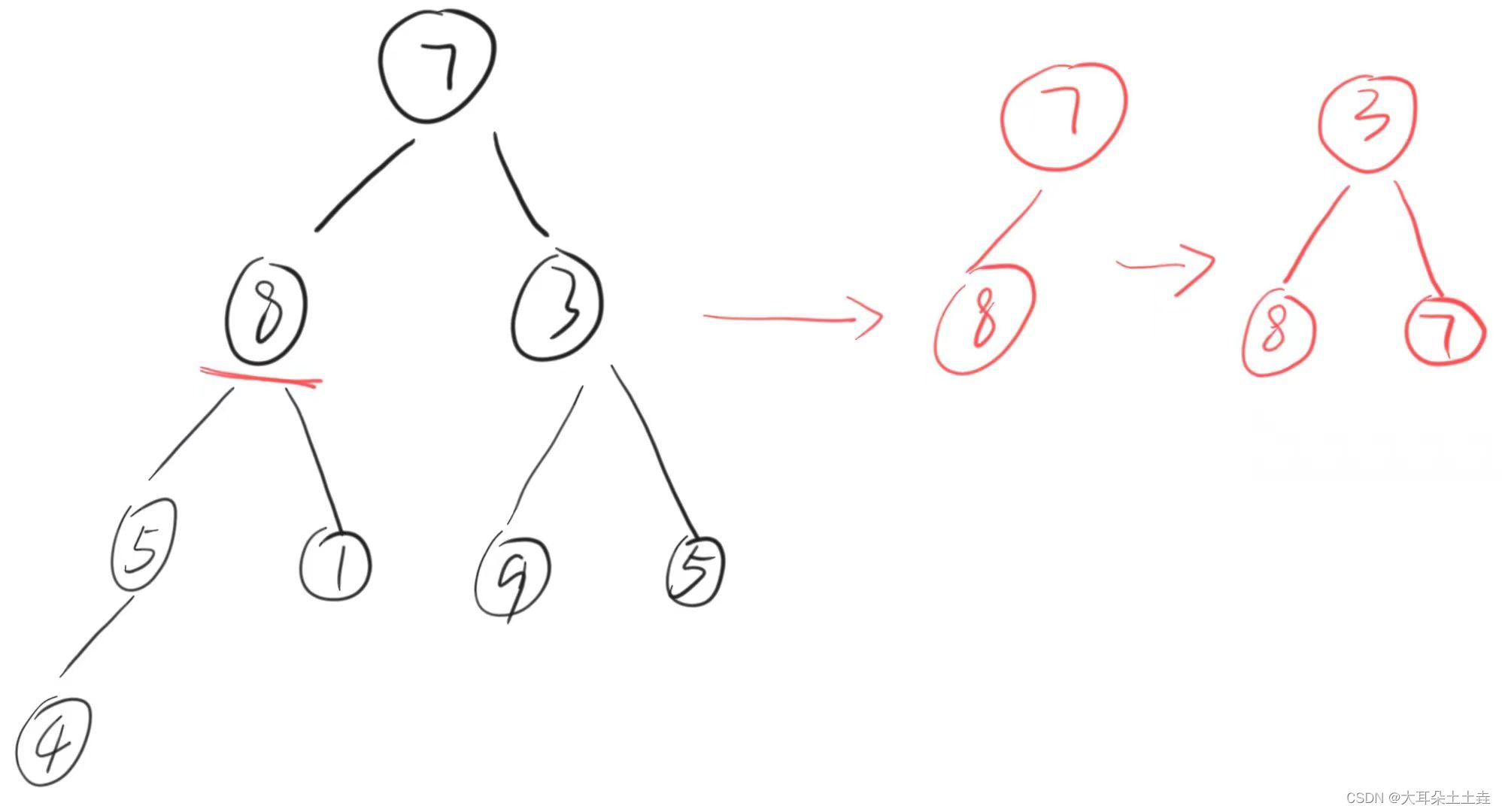
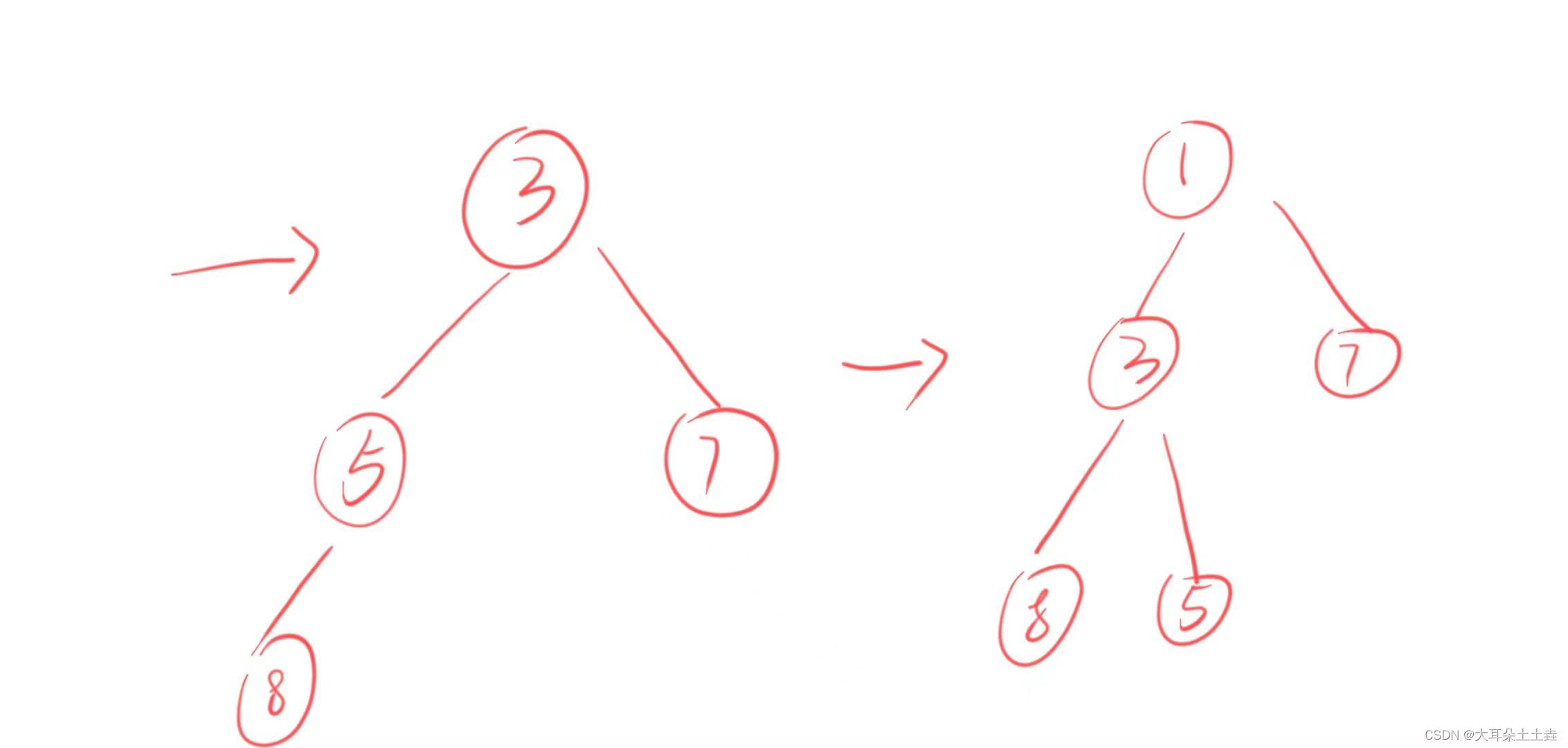
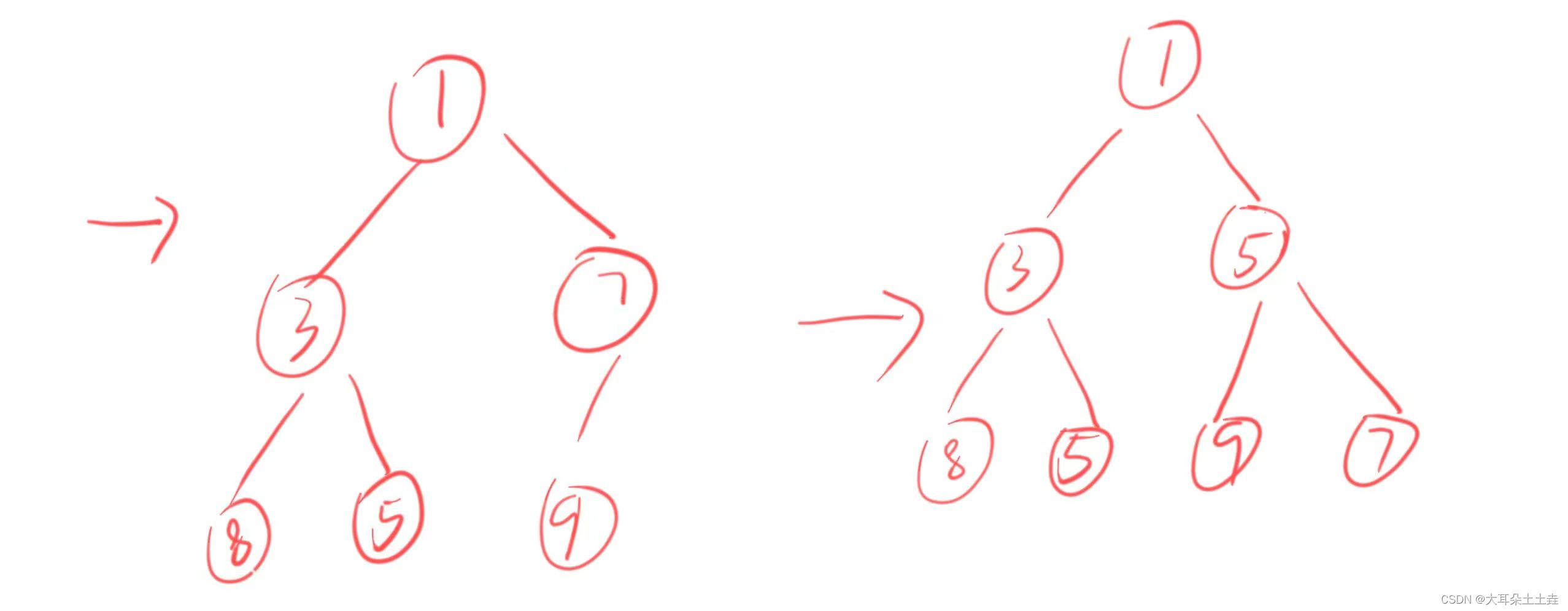
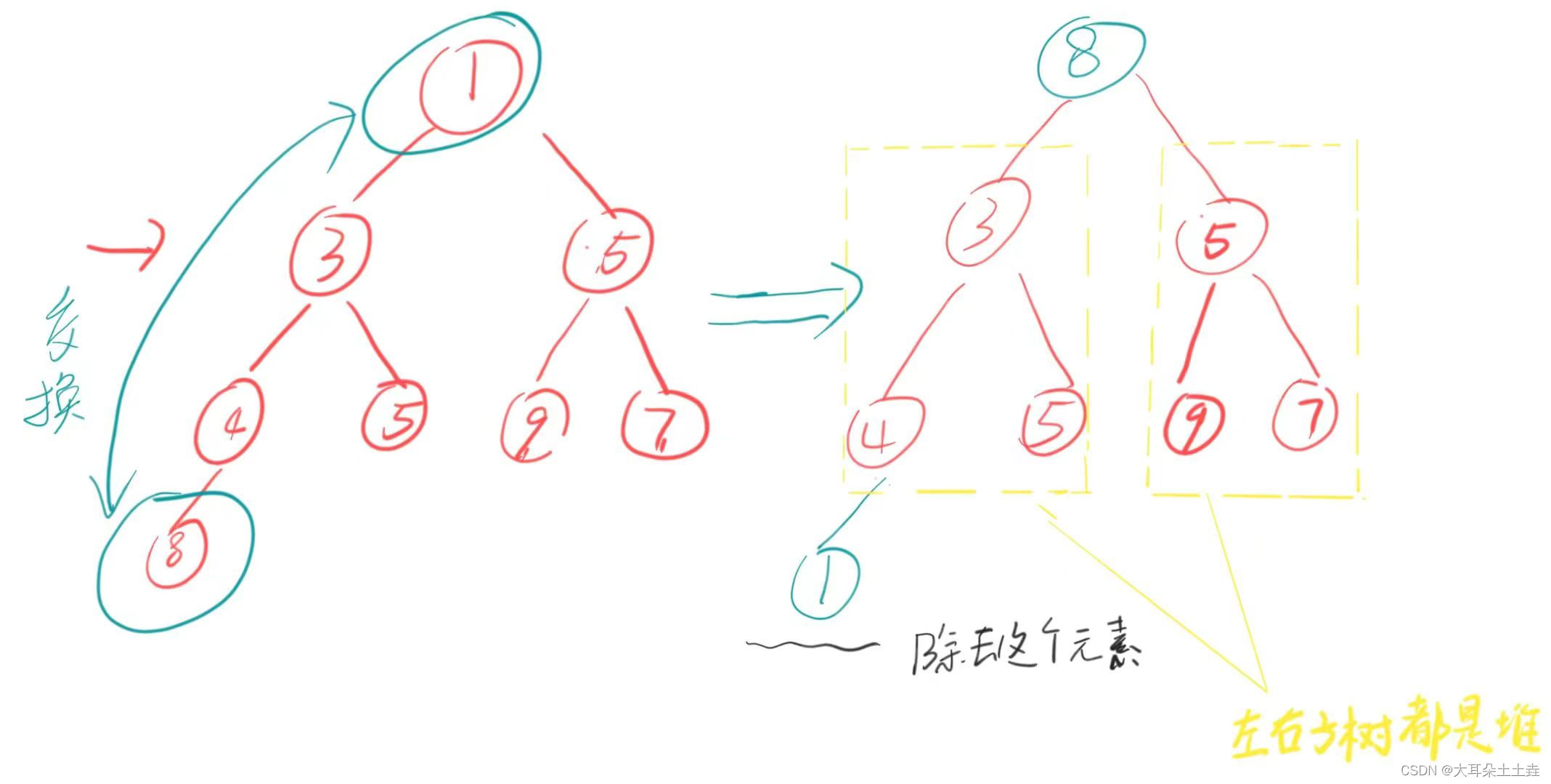
①交换首尾元素,将堆中最小的元素(首元素)换到尾部;
②将交换后的尾部元素忽略,剩余元素利用堆向下调整算法(除头外左右子树都是堆)调整为堆;
③重复②直到全部排完,得到降序数组:
代码如下:
//排序
int end = size-1;//堆底元素下标
while (end)
{Swap(&a[0], &a[end]);AdjustDown(a, end, 0);end--;
}
🤩🤩Swap函数在这里:
//交换函数
void Swap(HPDataType* a, HPDataType* b)
{HPDataType tmp = *a;*a = *b;*b = tmp;
}
(3)完整实现🥳🥳
void HeapSort(int* a,int size)
{//从第二个数据开始向上调整建堆for (int i = 1; i < size; i++){AdjustUp(a, i);}//排序int end = size-1;//堆底元素下标while (end){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);end--;}}
int main()
{int a[] = { 7,8,3,5,1,9,5,4 };HeapSort(a, 8);return 0;
}
结果如下:
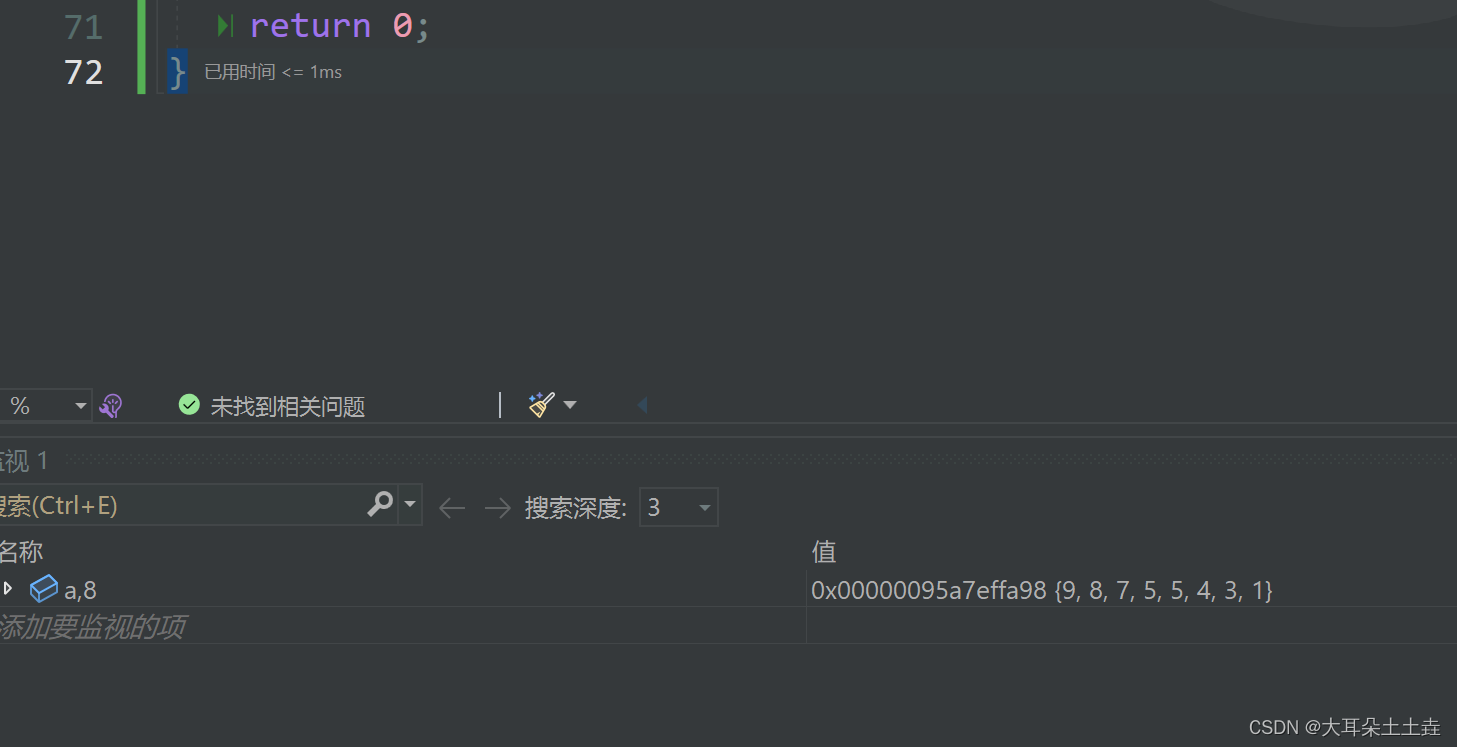
✨✨思考:如果我们要排升序应该利用什么堆呢?相信大家通过上面的学习与理解都知道应该用大堆对不对?具体代码大家可以参考上面小堆实现降序来自己试着写一写哦~
三、结语
以上就是堆的应用——堆排序啦~,我们发现可以不用写堆的实现代码就可以将一个数组排成堆🥳🥳,关键在于堆向上调整与向下调整算法的理解与运用,大家都学废了吗 ,💞💞 完结撒花 ~🎉🎉🎉
相关文章:

数据结构——堆的应用 堆排序详解
💞💞 前言 hello hello~ ,这里是大耳朵土土垚~💖💖 ,欢迎大家点赞🥳🥳关注💥💥收藏🌹🌹🌹 💥个人主页&#x…...
Sftp服务器搭建(linux)
Sftp服务器搭建(linux) 一、基本工作原理 FTP的基本工作原理如下: 1)建立连接:客户端与服务器之间通过TCP/IP建立连接。默认情况下,FTP使用端口号21作为控制连接的端口。 2)身…...
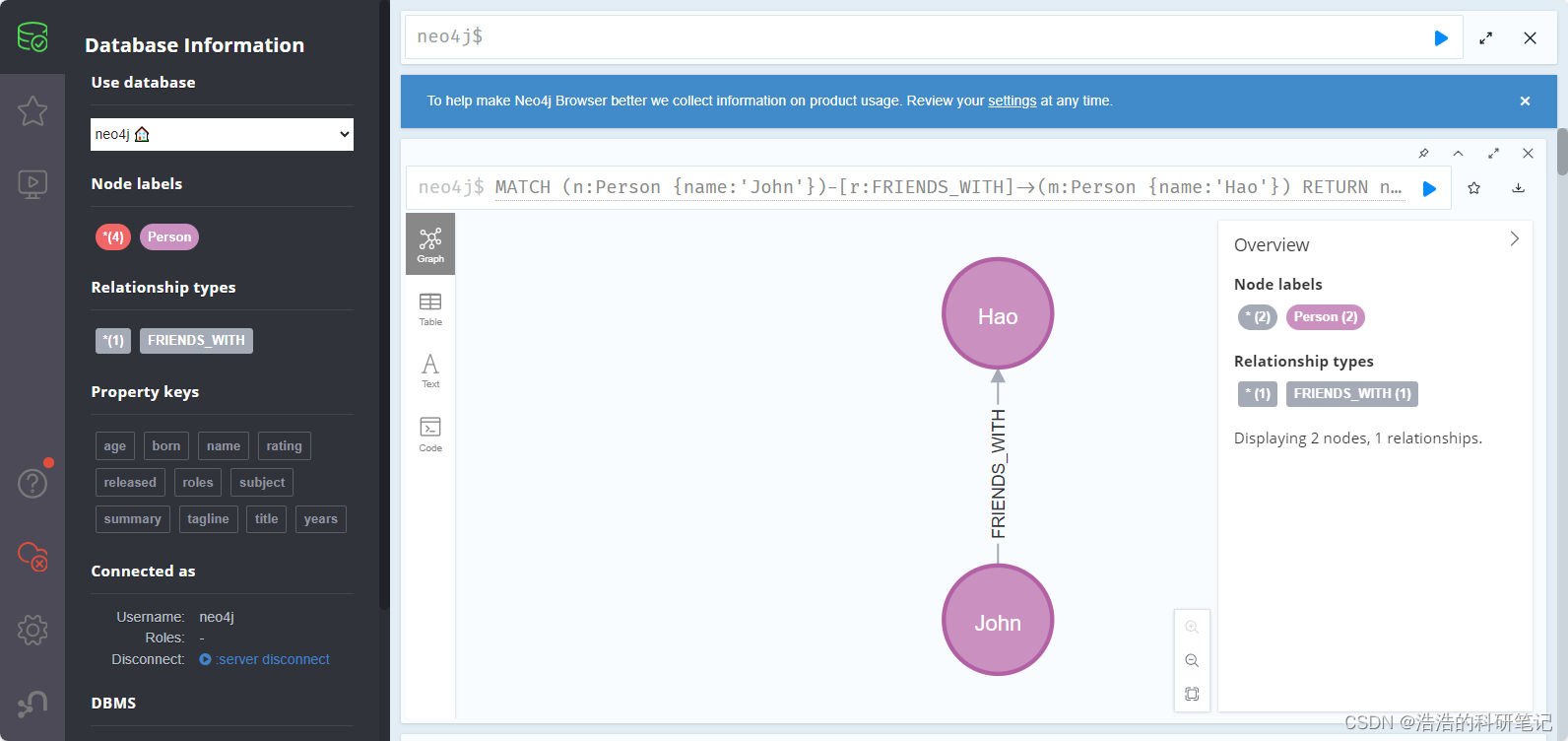
Neo4j 新手教程 环境安装 基础增删改查 python链接 常用操作 纯新手向
Neo4j安装教程🚀 目前在学习知识图谱的相关内容,在图数据库中最有名的就是Neo4j,为了降低入门难度,不被网上很多华丽呼哨的Cypher命令吓退,故分享出该文档,为自己手动总结,包括安装环境,增删改查…...
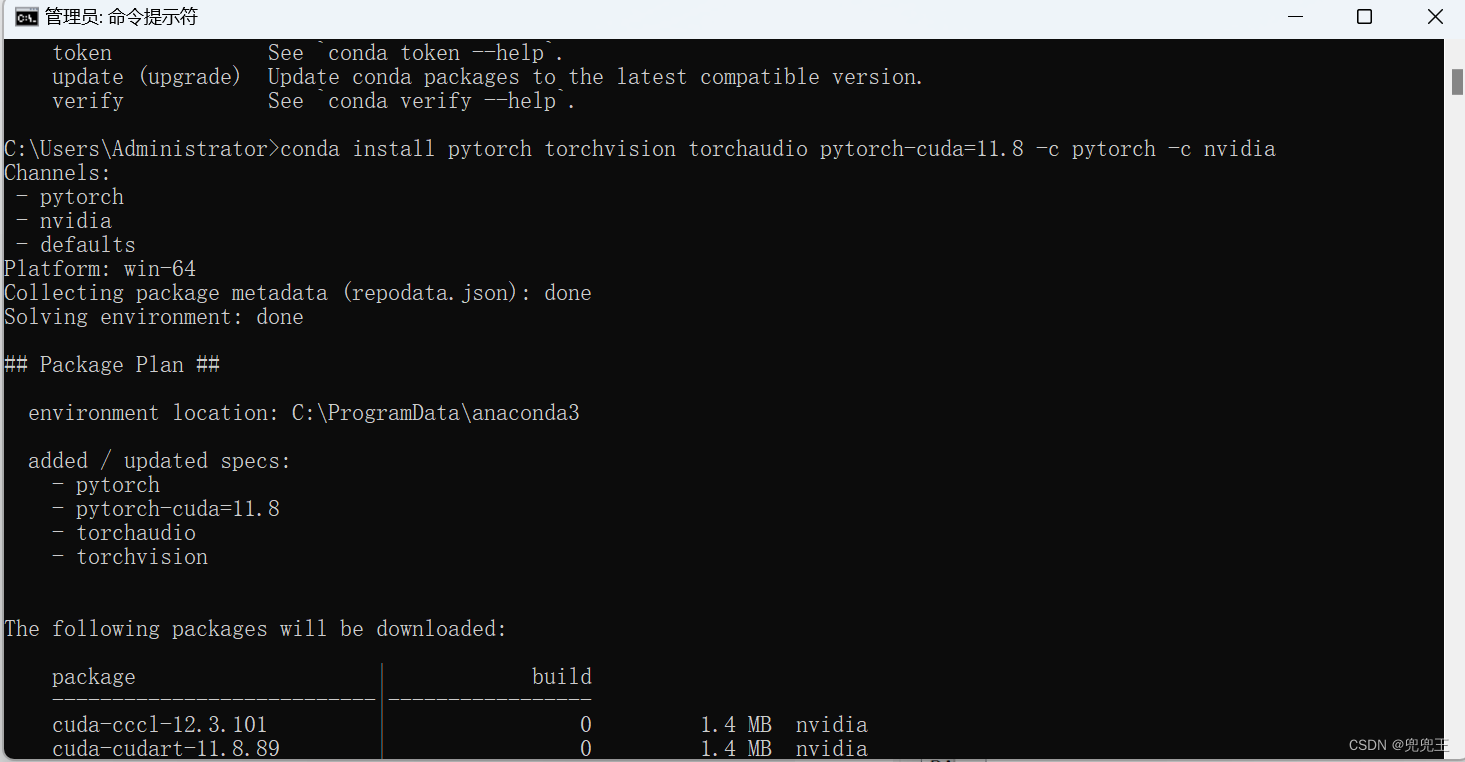
PyTorch2.0 环境搭建详细步骤(Nvidia显卡)
Step 1 、查看显卡驱动版本 Step2、下载CUDA 11.7 或者11.8(我自己用的这个)也行,稍后我会贴出来版本匹配对应表 https://developer.nvidia.com/cuda-toolkit-archive Step3、下载CUDNN cuDNN 9.0.0 Downloads | NVIDIA Developer Step4、安装anconda&…...

Python逆向:pyc字节码转py文件
一、 工具准备 反编译工具:pycdc.exe 十六进制编辑器:010editor 二、字节码文件转换 在CTF中,有时候会得到一串十六进制文件,通过010editor使用查看后,怀疑可能是python的字节码文件。 三、逆向反编译 将010editor得到…...

提示词工程技术:类比、后退、动态少样本、自动生成CoT
类比提示 “类比提示”利用类比推理的概念,鼓励模型生成自己的例子和知识,从而实现更灵活和高效的解决问题。 后退提示 “后退提示”专注于抽象,引导模型推导出高级概念和原理,进而提高其推理能力。 使用一个基本的数学问题来…...

【深度学习笔记】6_5 RNN的pytorch实现
注:本文为《动手学深度学习》开源内容,部分标注了个人理解,仅为个人学习记录,无抄袭搬运意图 6.5 循环神经网络的简洁实现 本节将使用PyTorch来更简洁地实现基于循环神经网络的语言模型。首先,我们读取周杰伦专辑歌词…...
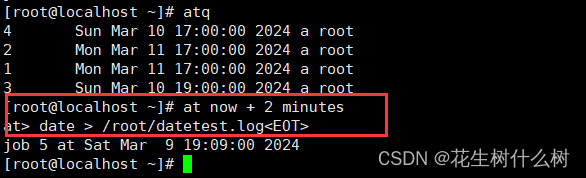
Linux at任务调度命令行编辑错误
错误: 在at任务调度命令行语句编辑错误时,按backspace进行删除无法进行。 解决方案: 请按Ctrlbackspace进行删除,即可解决。...

lua与C++粘合层框架
lua调用C++ 在lua中是以函数指针的形式调用函数, 并且所有的函数指针都必须满足如下此种类型: typedef int (*lua_CFunction) (lua_State *L); 也就是说, 偶们在C++中定义函数时必须以lua_State为参数, 以int为返回值才能被Lua所调用. 但是不要忘记了, 偶们的lua_State是支…...

POST 请求,Ajax 与 cookie
POST 请求则需要设置RequestHeader告诉后台传递内容的编码方式以及在 send 方法里传入对应的值 xhr.open("POST", url, true); xhr.setRequestHeader(("Content-Type": "application/x-www-form-urlencoded")); xhr.send("key1value1&…...
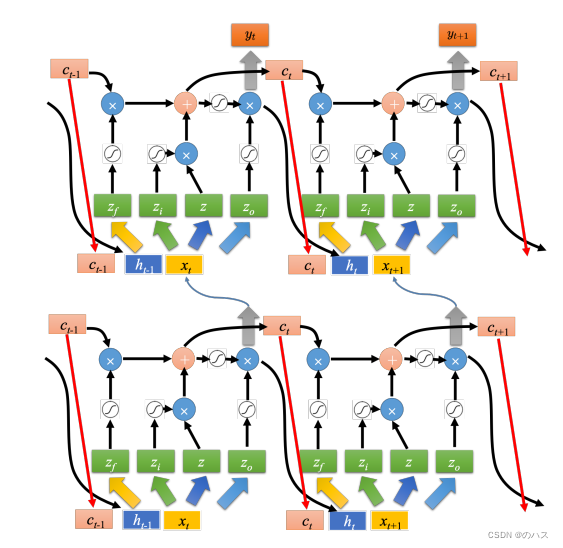
机器学习--循环神经网络(RNN)3
本篇文章结合具体的例子来介绍一下LSTM运算方式以及原理。请结合上篇文章的介绍食用。 一、具体例子 如上图所示,网络里面只有一个 LSTM 的单元,输入都是三维的向量,输出都是一维的输出。 这三维的向量跟输出还有记忆元的关系是这样的。 假设…...
Android Studio编译及调试知识
文章目录 Android Studio编译kotlin项目Android Studio编译Java和kotlin混合项目的过程gradle打印详细错误信息,类似这种工具的使用Android apk 从你的代码到APK打包的过程,APK安装到你的Android手机上的过程,最后安装好的形态,以…...
Fastjson 1.2.24 反序列化导致任意命令执行漏洞复现(CVE-2017-18349)
写在前面 CVE-2017-18349 指的是 fastjson 1.2.24 及之前版本存在的反序列化漏洞,fastjson 于 1.2.24 版本后增加了反序列化白名单; 而在 2019 年,fastjson 又被爆出在 fastjson< 1.2.47 的版本中,攻击者可以利用特殊构造的 …...

Spring Boot 注解教程
Spring Boot 注解教程 在 Spring 和 Spring Boot 的世界里,注解(Annotations)起着至关重要的作用。它们为开发者提供了声明式编程的能力,大大简化了 Spring 应用的开发过程。在这篇博客中,我们将探讨 Spring Boot 中的…...
Day32-计算机基础2
Day32-计算机基础2 1. 什么是网络拓扑(Network Topology)?2. 网络拓扑3种经典模型2.1 网络拓扑结构-总线型2.2 网络拓扑结构-环形2.3 星型:2.4 网络拓扑结构总结 3.OSI网络模型概念*****3.1 OSI的概念:open system interconnect 开放系统互连…...
Stable Diffusion WebUI 中英文双语插件(sd-webui-bilingual-localization)并解决了不生效的情况
本文收录于《AI绘画从入门到精通》专栏,专栏总目录:点这里。 大家好,我是水滴~~ 本文介绍一款中英文对照插件 sd-webui-bilingual-localization,该插件可以让你的 Stable Diffusion WebUI 界面同时显示中文和英文,让我…...

AndroidStudio连不上adb报错ADB Connection Error
之前笔者一直通过AndroidStudio来看日志,也一直用的一套自己的SDK,用了好几年了。 但是突然有一天,AndroidStudio启动后就弹出警告窗:ADB Connection Error,如下: 在Event Log面板还持续性的输出&#x…...
)
Java程序员常用网站(推荐)
文章目录 一、下载网站1 Jdk下载2 清华大学开源软件镜像站2.1 Mysql下载 3 常见工具3.1 typora markdown文档编辑器3.2 Apifox 软件测试工具3.3 GIT3.4 Maven3.5 PDF转word3.6 office3.7 xmind 思维导图3.8 draw.io 画图 4 Java 技术书籍大全 PDF5 Java 8 编程思想中文版6 GitH…...
mq基础类设计
消息队列就是把阻塞队列这样的数据结构单独提取成一个程序独立进行部署。——>实现生产者消费者模型。 但是阻塞队列是在一个进程内部进行的; 消息队列是在进程与进程之间进行实现的, 解耦合:就是在分布式系统中,A服务器调用B…...
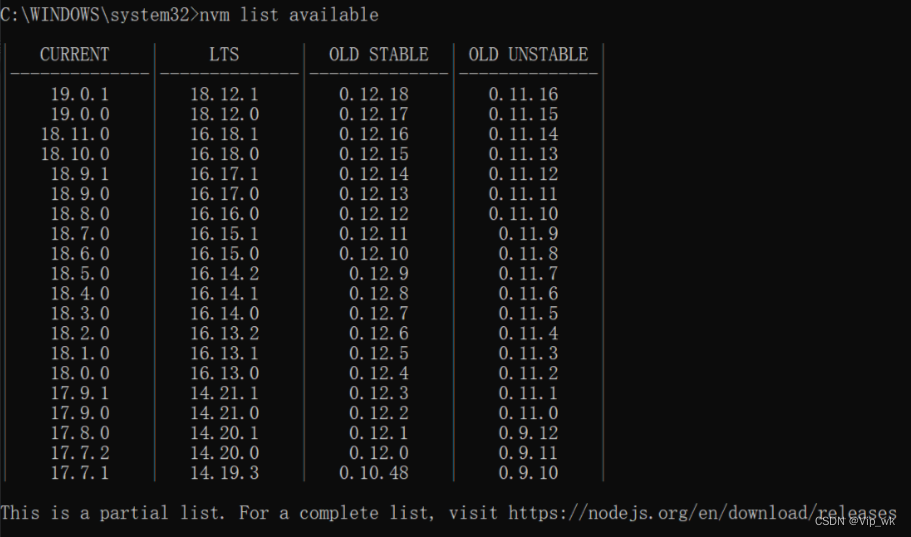
【Node.js从基础到高级运用】二、搭建开发环境
Node.js入门:搭建开发环境 在上一篇文章中,我们介绍了Node.js的基础概念。现在,我们将进入一个更实际的阶段——搭建Node.js的开发环境。这是每个Node.js开发者旅程中的第一步。接下来,我们将详细讨论如何安装Node.js和npm&#…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...