基于Kronig-Penney能带模型的MATLAB求解与仿真
目录
1.程序功能描述
2.测试软件版本以及运行结果展示
3.核心程序
4.本算法原理
5.完整程序
1.程序功能描述
基于Kronig-Penney能带模型的MATLAB求解与仿真.综合利用 MATLAB提供的求解常微分方程、矩阵行列式、代数表达式化简及绘图等函数 ,可使 Kronig-Penney能带模型分析计算的工作量大为减少。
2.测试软件版本以及运行结果展示
MATLAB2013b版本运行

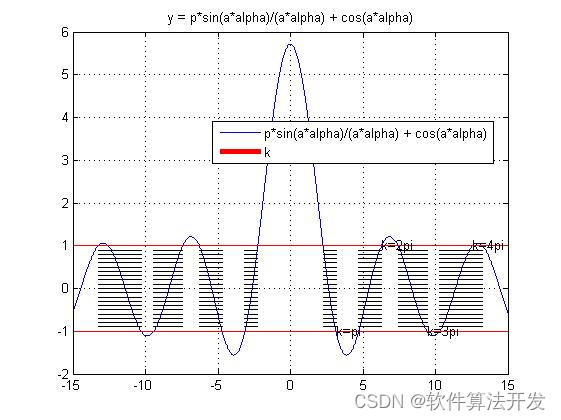
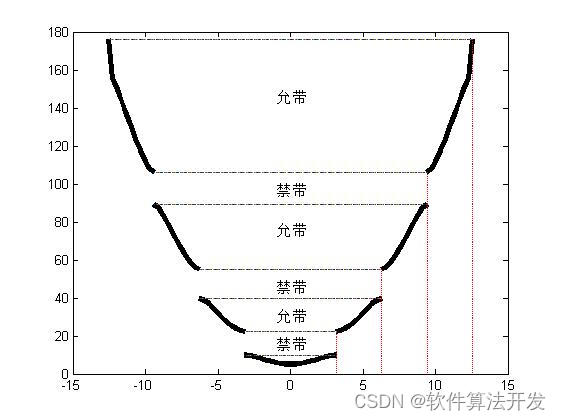


3.核心程序
.........................................................................
%DDDD
startpoint = 10.3040;
endpoint = 13.2755;
N = 10000;
k = -4*pi:(2*pi)/20:-3*pi;
for i = 1:length(k)
alpha2(i) = solvealpha(startpoint,endpoint,N,k(i));
alpha2(i) = alpha2(i)*alpha2(i);
end
plot(k,alpha2,'k','LineWidth',4);hold on;
plot(k+4*pi,alpha2,'k','LineWidth',1);hold on;
k = 3*pi:(2*pi)/20:4*pi;
for i = 1:length(k)
alpha2(i) = solvealpha(startpoint,endpoint,N,k(i));
alpha2(i) = alpha2(i)*alpha2(i);
end
plot(k,alpha2,'k','LineWidth',4);hold on;
plot(k-4*pi,alpha2,'k','LineWidth',1);hold on;
clear k
clear alpha2%画虚线
plot(-4*pi,0:2:200,'r');hold on;
plot(-3*pi,0:2:200,'r');hold on;
plot(-2*pi,0:2:200,'r');hold on;
plot(-pi, 0:2:200,'r');hold on;
plot(0, 0:0.1:200,'r');hold on;
plot(pi, 0:2:200,'r');hold on;
plot(2*pi,0:2:200,'r');hold on;
plot(3*pi,0:2:200,'r');hold on;
plot(4*pi,0:2:200,'r');hold on;
saveas(gcf,'6.jpg');
16_007m4.本算法原理
基于Kronig-Penney能带模型的MATLAB求解与仿真.综合利用 MATLAB提供的求解常微分方程、矩阵行列式、代数表达式化简及绘图等函数 ,可使 Kronig-Penney能带模型分析计算的工作量大为减少。
Kronig-Penney模型是一种一维周期势垒模型,用于描述晶体中电子在周期性势场中的运动特性,从而推导出晶体的能带结构。该模型由 Ralph Kronig 和 Hans Bethe 在1930年代提出,主要用来简化对固体晶格中原子间复杂相互作用的研究。在一个理想的无限大一维晶格中,原子排列形成周期性的势场。Kronig-Penney模型假设每个原子或离子贡献一个简化的无限深势阱(代表原子间的共价键)和一个有限高的势垒(表示原子间的排斥力)。模型将晶格简化为一系列等间距、具有相同宽度 a 的无限深势阱与有限高势垒相间隔的结构。

Kronig-Penney模型虽然简单,但它揭示了固体中电子能带结构的一些基本特征。通过这个模型,我们可以理解带隙的形成机制以及能带宽度与势场参数的关系。这些理解对于半导体物理和固体电子学的发展具有重要意义。
5.完整程序
VVV
相关文章:

基于Kronig-Penney能带模型的MATLAB求解与仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.本算法原理 5.完整程序 1.程序功能描述 基于Kronig-Penney能带模型的MATLAB求解与仿真.综合利用 MATLAB提供的求解常微分方程、矩阵行列式、代数表达式化简及绘图等函数 ,可使 Kronig-Penney能带模型分析…...

【Web - 框架 - Vue】随笔 - Vue CLI - 快速上手
Vue CLI 创建Vue CLI项目 【步骤】 命名项目空间:在电脑里创建文件夹,用于存储所有项目;定位项目空间:在"CMD窗口"里定位到工程的项目空间上; 方法1:(a)用"WINR"打开运行窗口&#x…...
)
JavaWeb开发——html、 jsp(html 、js 、java源码)
1.前后端整体合一 在页面上,包含界面和业务数据处理 2.前后端分离 项目整体上分成前端部分和后端部分,相互独立 Jquery的核心 选择器----找到需要操作的Dom读取或者设置DOM的值或者属性事件的处理 一、jQuery选择器 $("标签类型")$("…...

javascript事件大全
在JavaScript中,事件是用户和浏览器之间交互的桥梁。当某些特定的事情发生时(如用户点击按钮、鼠标移动、页面加载等),浏览器会触发相应的事件。这些事件可以被JavaScript代码捕获,并允许开发者执行某些操作。以下是一…...

太平医康养经理人是医疗资源的链接者
太平人寿通过构建资源整合平台,已成功将国际化医疗服务资源进行深度整合。目前,该公司已完成对英国著名医疗集团Circle Health在中国设立的首家医疗机构——圆和医疗的增资行动,并与新加坡知名的莱佛士私立综合医疗集团签订了业务合作协议。同…...
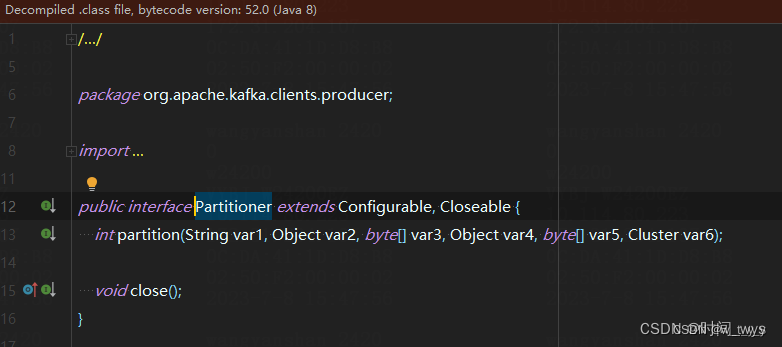
kafka(三)springboot集成kafka(1)介绍
基于kafka新版本 <dependencies><dependency><groupId>org.apache.kafka</groupId><artifactId>kafka-clients</artifactId><version>3.0.0</version></dependency> </dependencies> 一、kafkaProducer 1、介绍…...

Markdown语法与基础使用
在撰写博客、文档或者其他类型的文字内容时,Markdown语法是一种简洁、易读易写的标记语言,被广泛应用于互联网上的文本编辑和排版中。下面将介绍Markdown语法的基础使用方法,帮助你更好地利用Markdown来编写内容。 1. 标题 Markdown支持使用…...

【排序】七大排序表格比较
排序 时间复杂度 空间复杂度 最坏时间复杂度 最好时间复杂度 稳定性 插入排序 O(n) O(1) O(n) O(n) 稳定 希尔排序 O(nlogn)-O(n)取决于增量序列 O(1) O(n^1.3) O(nlogn) 不稳定 选择排序 O(n) O(1) O(n) O(n) 不稳定 冒泡排序 O(n) O(1) O(n) O(n…...
arcgis 栅格数据处理2——栅格转地级市(栅格转矢量图)
1. 获取空间分析权限(解决无法执行所选工具问题) 选中“自定义”中的“扩展模块” 在弹出的模块中选中能选的模块,此处需要选择“spatial analysis”以进行下一步分析 3. 将栅格数据转为整数型(解决无法矢量化) 选…...
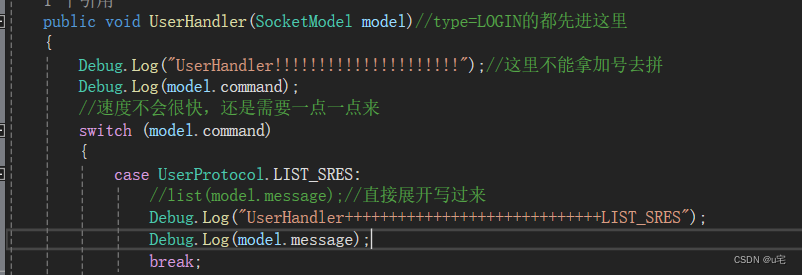
unity学习(53)——选择角色界面--分配服务器返回的信息
好久没写客户端了,一上手还不太适应 1.经过测试,成功登陆后,客户端请求list_request,成功返回,如下图: 可见此时model第三个位置的参数是1.也成功返回了所有已注册角色的信息。 2.之前已知创建的角色信息…...

矩阵爆破逆向-条件断点的妙用
不知道你是否使用过IDA的条件断点呢?在IDA进阶使用中,它的很多功能都有大作用,比如:ida-trace来跟踪调用流程。同时IDA的断点功能也十分强大,配合IDA-python的输出语句能够大杀特杀! 那么本文就介绍一下这个…...

logstash和elasticsearch的几种交互接口
Logstash与Elasticsearch是两个非常流行的开源工具,用于处理和存储大量的日志数据。它们之间的集成非常重要,因为Logstash用于收集、处理和转换日志数据,而Elasticsearch用于存储、搜索和分析这些数据。在本文中,我们将详细介绍Lo…...

Golang 开发实战day02 - Print Formatting
Golang 教程02 - Print,Formatting Strings Go语言提供了丰富的格式化字符串功能,用于将数据格式化为特定格式的字符串。本课程将详细介绍Go语言中Print和Formatting Strings的用法,并提供代码示例供大家参考。 1.Print 类型及使用 1.1 Pr…...
2023护网蓝初面试
目录 一、渗透测试的流程 二、常见的漏洞 三、中间件漏洞 四、SQL注入原理、种类?防御?预编译原理,宽字节注入原理 预编译原理: 宽字节注入原理: 五、XSS的种类有哪些?区别?修复…...
Unity编辑器功能Inspector快捷自动填充数据和可视化调试
我们有时候可能需要在面板增加一些引用,可能添加脚本后要手动拖动,这样如果有大量的脚本拖动也是不小的工作量 实例 例如:我的脚本需要添加一个Bone的列表,一个个拖动很麻烦。 实现脚本 我们可以用这样的脚本来实现。 public…...

【C/C++】常量指针与指针常量的深入解析与区分(什么是const int * 与 int * const ?)
目录 一、前言 二、const 的简单介绍 三、常量指针 🔍介绍与分析 📰小结与记忆口诀 四、指针常量 🔍介绍与分析 📰小结与记忆口诀 五、总结与提炼 六、共勉 一、前言 在【C/C】的编程中,指针与const关键字的组合…...

零、自然语言处理开篇
目录 0、NLP任务的基础——符号向量化 0.0 词袋模型 0.1 查表/One-hot编码 0.2 词嵌入模型/预训练模型 0.2.0 Word2Vec (0)CBOW (1)Skip-gram 0.2.1 GloVe 0.2.2 WordPiece 0.2.3 BERT 0.2.4 ERNIE NLP自然语言处理&am…...
Learn OpenGL 04 纹理
纹理环绕方式 纹理坐标的范围通常是从(0, 0)到(1, 1),那如果我们把纹理坐标设置在范围之外会发生什么?OpenGL默认的行为是重复这个纹理图像(我们基本上忽略浮点纹理坐标的整数部分),但OpenGL提供了更多的选择…...

了解开源可视化表单的主要优势
为什么可视化表单深受大家喜爱?这就需要了解开源可视化表单的优势和特点了。在流程化办公深入人心的今天,提高办公协作效率早已成为大家的发展目标,低代码技术平台、开源可视化表单是提升办公协作效率的得力助手,一起来看看它的优…...
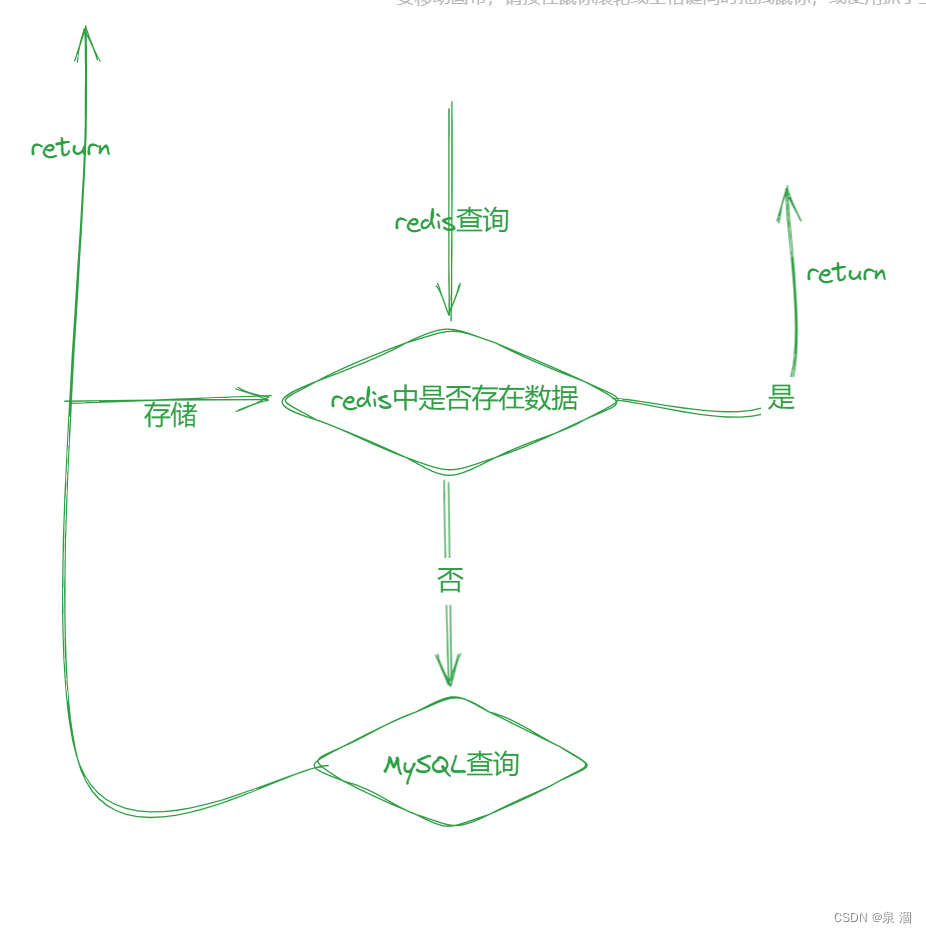
Redis进阶--一篇文章带你走出Redis
目录 什么是Redis?? Redis有哪些使用场景? Redis是单线程还是多线程? 为什么Redis是单线程速度还是很快?? Redis持久化 RDB机制:(Redis DataBase) [是redis中默认的持久化方式] AOF机制:(Append Only File) Redis和MySQL如何保持数据一致????…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

十九、【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建
【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建 前言准备工作第一部分:回顾 Django 内置的 `User` 模型第二部分:设计并创建 `Role` 和 `UserProfile` 模型第三部分:创建 Serializers第四部分:创建 ViewSets第五部分:注册 API 路由第六部分:后端初步测…...
