背包问题算法
背包问题算法
- 0-1背包问题
- 二维数组
- 一维数组
- 完全背包问题
- 二维数组
- 一维数组
- 多重背包问题
- 一维数组
0-1背包问题
问题:背包的容量为9,有重量分别为[2, 4, 6, 9]的四个物品,价值分别为[3, 4, 5, 6],求背包能装的物品的最大价值是多少,每种物品的数量最多为1
二维数组
w = [2, 4, 6, 9] # 重量
v = [3, 4, 5, 6] # 价值
c = 9 # 最大容量
n = len(w) # 物品数量
w.insert(0, 0)
v.insert(0, 0)
dp = [[0] * (c + 1) for _ in range(n + 1)]
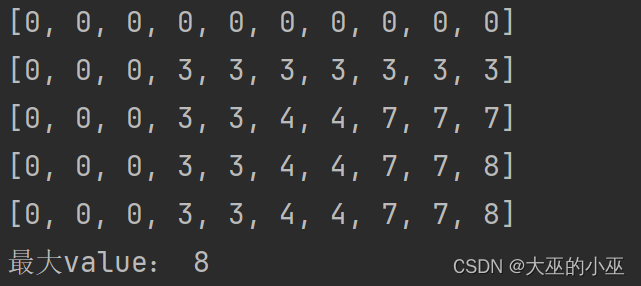
for i in range(1, n + 1):for j in range(1, c + 1): # 正向if j >= w[i]:dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i])else:dp[i][j] = dp[i - 1][j]for rows in dp:print(rows)
print('最大value:', dp[n][c])
一维数组
w = [2, 4, 6, 9] # 重量
v = [3, 4, 5, 6] # 价值
c = 9 # 最大容量n = len(w) # 物品数量
w.insert(0, 0)
v.insert(0, 0)
dp = [0] * (c + 1)
for i in range(1, n + 1):for j in range(c, 0, -1): # 逆向if j >= w[i]:dp[j] = max(dp[j], dp[j - w[i]] + v[i])print(dp)
print('最大value:', dp[c])

完全背包问题
问题:背包的容量为9,有重量分别为[2, 4, 6, 9]的四个物品,价值分别为[3, 4, 5, 6],求背包能装的物品的最大价值是多少,每种物品的数量最多不限
二维数组
w = [2, 4, 6, 9] # 重量
v = [3, 4, 5, 6] # 价值
c = 9 # 最大容量n = len(w)
w.insert(0, 0)
v.insert(0, 0)dp = [[0] * (c + 1) for _ in range(n + 1)]for i in range(1, n + 1):for j in range(1, c + 1): # 正向if j >= w[i]:dp[i][j] = max(dp[i - 1][j], dp[i][j - w[i]] + v[i])else:dp[i][j] = dp[i - 1][j]
for values in dp:print(values)
print('最大value:', dp[n][c])

一维数组
w = [2, 4, 6, 9] # 重量
v = [3, 4, 5, 6] # 价值
c = 9 # 最大容量n = len(w)w.insert(0, 0)
v.insert(0, 0)dp = [0] * (c + 1)for i in range(1, n + 1):for j in range(0, c + 1): # 正向if j >= w[i]:dp[j] = max(dp[j], dp[j - w[i]] + v[i])print(dp)
print('最大value:', dp[c])

多重背包问题
问题:背包的容量为10,有重量分别为[2, 4, 6, 9]的四个物品,价值分别为[3, 4, 5, 6],求背包能装的物品的最大价值是多少,每种物品的数量最多分别为[2, 1, 2, 1]
一维数组
w = [2, 4, 6, 9] # 重量
v = [3, 4, 5, 6]
counts = [2, 1, 2, 1] # 数量
c = 10 # 最大容量
n = len(w)w.insert(0, 0)
v.insert(0, 0)
counts.insert(0, 0)dp = [0] * (c + 1)for i in range(1, n + 1):for j in range(c, 0, -1): # 逆向for k in range(1, counts[i] + 1):if j >= k * w[i]:dp[j] = max(dp[j], dp[j - k * w[i]] + v[i])print(dp)
print('最大value:', dp[c])

相关文章:

背包问题算法
背包问题算法 0-1背包问题二维数组一维数组 完全背包问题二维数组一维数组 多重背包问题一维数组 0-1背包问题 问题:背包的容量为9,有重量分别为[2, 4, 6, 9]的四个物品,价值分别为[3, 4, 5, 6],求背包能装的物品的最大价值是多少…...
echarts柱状图可鼠标左击出现自定义弹框,右击隐藏弹框并阻止默认右击事件
每项x轴数据对应有两条柱图和一条阴影效果是学习其它博客得到的效果,这个是学习的原文链接:echarts两个合并柱体(普通柱状图象形柱图)共享一个柱体阴影 因为这次情况比较特殊,不仅需要自定义弹框内容,而且…...
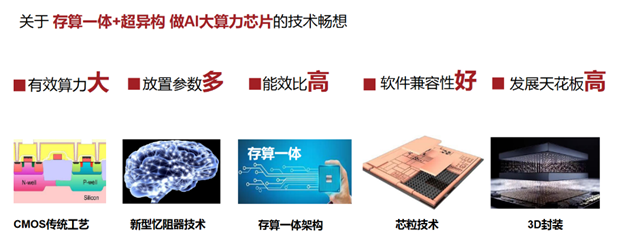
存算一体成为突破算力瓶颈的关键技术?
大模型的训练和推理需要高性能的算力支持。以ChatGPT为例,据估算,在训练方面,1746亿参数的GPT-3模型大约需要375-625台8卡DGX A100服务器训练10天左右,对应A100 GPU数量约3000-5000张。 在推理方面,如果以A100 GPU单卡…...

Pytorch_1_基本语法
一、Pytorch的基本元素操作 1.引入torch from __future__ import print_function import torch 2.创建矩阵 x torch.empty(5,3) print(x) 3.输出结果: tensor([[7.9191e34, 1.1259e24, 1.2359e-42], [4.0824e-40, 1.1379e-35, 2.5353e30], [8.…...

2024上海国际玻璃纤维及新材料展览会
2024上海国际玻璃纤维及新材料展览会 时间:2024年12月18~20日 地点:上海新国际博览中心 ◆ 》》》展会概况: 玻璃纤维是一种性能优异的无机非金属材料,比有机纤维耐温高,不燃,抗腐ÿ…...

云计算项目九:K8S安装
K8S安装 Kube-master安装 按照如下配置准备云主机 防火墙相关配置:禁用selinux,禁用swap,且在firewalld-*。上传kubernetes.zip 到跳板机 配置yum仓库(跳板机) 跳板机主机配置k8s软件源服务端 [rootjs ~]# yum -y…...
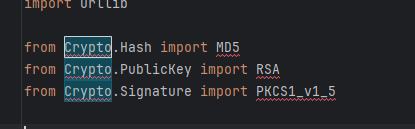
sign加密方法生成
1. 引入包的问题 2. 原因 .pycrypto、pycrytodome和crypto是一个东西,crypto在python上面的名字是pycrypto,它是一个第三方库,但是已经停止更新 3. 解决方法 --直接安装:pip install pycryptodome 3.但是,在使用的时…...

【Linux】编译器-gcc/g++使用
个人主页 : zxctscl 文章封面来自:艺术家–贤海林 如有转载请先通知 文章目录 1. 前言2. 初见gcc和g3. 程序的翻译过程3.1 预处理3.1.1 宏替换 去注释 头文件展开3.1.2 条件编译 3.2 编译3.3 汇编3.4 链接 4. 链接4.1 动态链接4.2 静态链接 1. 前言 在之…...
 函数:筛选可迭代对象元素)
Python 中的 filter() 函数:筛选可迭代对象元素
在 Python 中,filter() 函数是一个非常有用的内置函数,用于根据指定条件过滤可迭代对象中的元素。本文将深入探讨 filter() 函数的用法、工作原理以及常见应用场景,以帮助大家更好地理解和运用这个函数。 什么是 filter() 函数? …...

Java高频面试之并发篇
有需要互关的小伙伴,关注一下,有关必回关,争取今年认证早日拿到博客专家 并行和并发有什么区别? 并行是同时执行多个任务,而并发是多个任务在一段时间内交替执行。并行(Parallel)是指同时执行多个任务或操作,通过同时…...
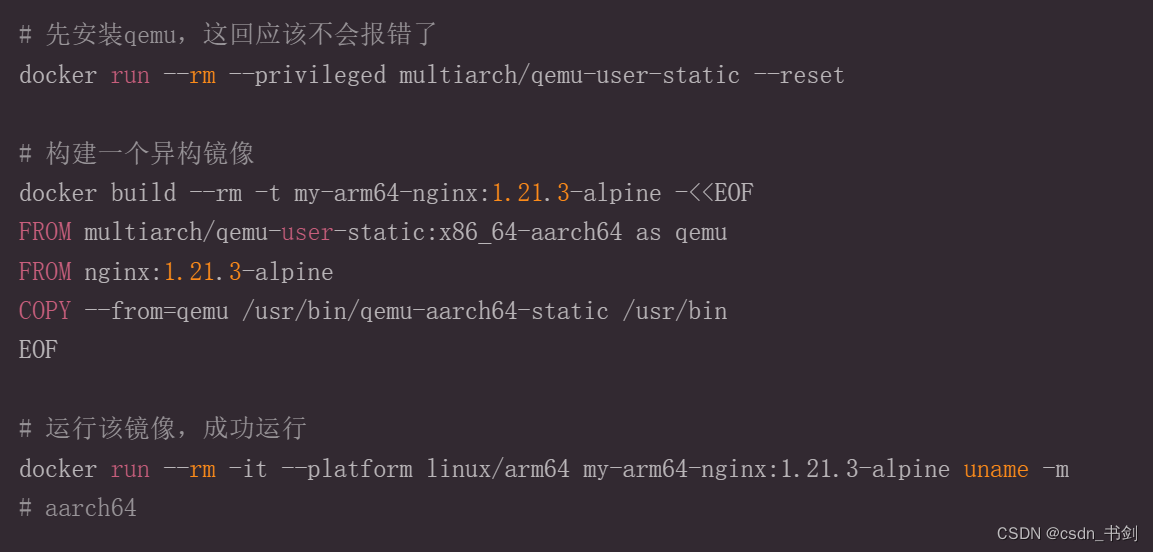
docker 运行异构镜像
概述 关于docker镜像在不同的cpu架构下运行报错的解决办法,作者踩坑验证,在此分享经验 某次工作遇到需要银行内部部署docker镜像,由于行内已经开始走信创的路线,使用鲲鹏系统,arm架构,记过就遇到了standa…...

练习3-8 查询水果价格
探索--题目集索引 给定四种水果,分别是苹果(apple)、梨(pear)、桔子(orange)、葡萄(grape),单价分别对应为3.00元/公斤、2.50元/公斤、4.10元/公斤、10.20元…...
 。void f(int *p){ *p = 5;}int main(void){ int a, *p; a = 10;)
PTA 对于下列程序,正确的是() 。void f(int *p){ *p = 5;}int main(void){ int a, *p; a = 10;
对于下列程序,正确的是() 。 void f(int *p) {*p 5; } int main(void) {int a, *p;a 10;p &a;f(p);printf(“%d”, (*p));return 0; }A.5 B.6 C.10 D.11 答:A 解析:这里考察当是指针作为函数的参数。这里将 p …...

【银河商学】大蓝短视频学习02——流量突围实战
【银河商学】大蓝短视频学习02——流量突围实战 内容大纲 找对标找准你的"竞争对手" 定形式选定适合你的视频形式 做内容选题决定命运 2s上热门 一、找对标 1. 为什么要找对标 标准答案,少走弯路99%的问题,都有标准答案。 找个懂得人问一问 秒上热门,快速起号预…...

Android 获取Sms
Android 获取Sms 本篇文章记录下android下获取短信列表. 1: 申请权限 <uses-permission android:name"android.permission.READ_SMS" />2: 获取短信内容列表 private void readSms() {String[] projection {"_id", "address", "b…...
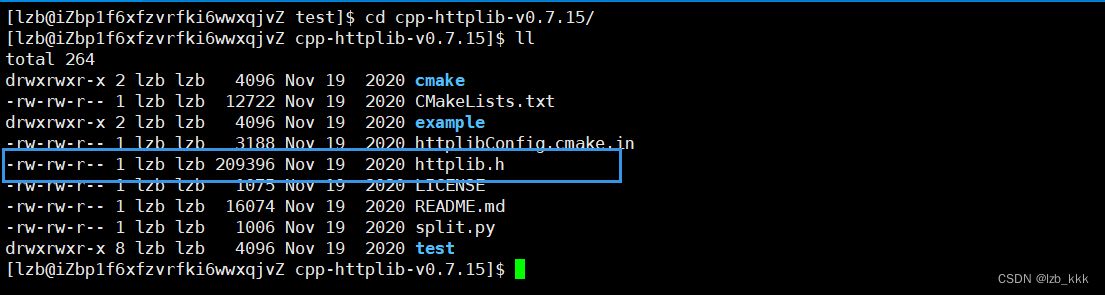
【Linux】cpp-httplib库
目录 升级gcc版本 下载cpp-httplib的zip安装包,上传到服务器 编辑 简单使用 首先打开gittee,搜索cpp-httplib,选择其中一个即可 也可以点下方链接 cpp-httplib库:cpp-httplib: cpp-httplib (gitee.com) 注意:cpp-httplib在使用的时候需…...

全网最最最详细centos7如何安装docker教程
在CentOS 7上安装Docker主要包括以下步骤: 1. 卸载旧版本的Docker 首先,需要确保系统上没有安装旧版本的Docker。可以通过以下命令来卸载它们: sudo yum remove docker \docker-client \docker-client-latest \docker-common \docker-late…...

【C++专栏】C++入门 | 函数重载、引用、内联函数
博客主页:Duck Bro 博客主页系列专栏:C专栏关注博主,后期持续更新系列文章如果有错误感谢请大家批评指出,及时修改感谢大家点赞👍收藏⭐评论✍ C入门 | 函数重载、引用、内联函数 文章编号:C入门 / 02 文…...

html--彩虹爱心
文章目录 js内容cssreset.min.cssstyle.css html内容 js内容 const colors ["#e03776","#8f3e98","#4687bf","#3bab6f","#f9c25e","#f47274"]; const SVG_NS http://www.w3.org/2000/svg; const SVG_XLINK &q…...

基于Kronig-Penney能带模型的MATLAB求解与仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.本算法原理 5.完整程序 1.程序功能描述 基于Kronig-Penney能带模型的MATLAB求解与仿真.综合利用 MATLAB提供的求解常微分方程、矩阵行列式、代数表达式化简及绘图等函数 ,可使 Kronig-Penney能带模型分析…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...

Chrome 浏览器前端与客户端双向通信实战
Chrome 前端(即页面 JS / Web UI)与客户端(C 后端)的交互机制,是 Chromium 架构中非常核心的一环。下面我将按常见场景,从通道、流程、技术栈几个角度做一套完整的分析,特别适合你这种在分析和改…...

离线语音识别方案分析
随着人工智能技术的不断发展,语音识别技术也得到了广泛的应用,从智能家居到车载系统,语音识别正在改变我们与设备的交互方式。尤其是离线语音识别,由于其在没有网络连接的情况下仍然能提供稳定、准确的语音处理能力,广…...
