美团春招编程第一场第三题
美团春招编程第一场第三题
题目
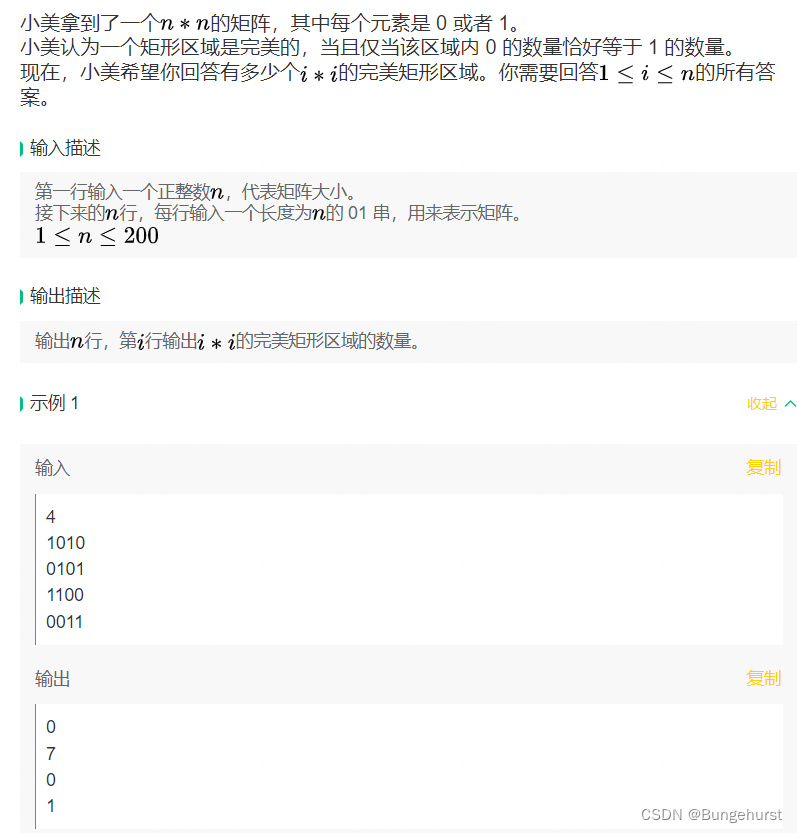
解答
- 思路-暴力解法
pair中存储从原点到包含当前元素的0,1数量,得到二维数组mat;
从头到尾遍历尺寸为i*i的矩形,计算完美矩形数量
#include <iostream>
#include <vector>
using namespace std;int main() {int n;cin >> n;vector<vector<pair<int, int>>> mat;vector<vector<int>> data;for (int i = 0; i < n; i++) {vector<pair<int, int>> dp(n);vector<int> tmp(n);if (i == 0) {for (int j = 0; j < n; j++) {int in;cin >> in;tmp[j] = in;if (j == 0) {dp[j] = {in == 1 ? 1 : 0, in == 0 ? 1 : 0};} else {dp[j] = {dp[j - 1].first + (in == 1 ? 1 : 0), dp[j - 1].second + (in == 0 ? 1 : 0)};}}} else {for (int j = 0; j < n; j++) {int in;cin >> in;tmp[j] = in;if (j == 0) dp[j] = {in == 1 ? 1 : 0, in == 0 ? 1 : 0};else dp[j] = {dp[j - 1].first + (in == 1 ? 1 : 0), dp[j - 1].second + (in == 0 ? 1 : 0)};}for (int j = 0; j < n; j++) {dp[j].first += mat[i - 1][j].first;dp[j].second += mat[i - 1][j].second;}}data.emplace_back(tmp);mat.emplace_back(dp);}for (int i = 1; i <= n; i++) {if (i == 1) {cout << 0 << endl;continue;} else {int ret = 0;for (int k = 0; k <= n - i; k++) {for (int p = 0; p <= n - i; p++) {if(k == 0 && p == 0) {if(mat[k+i-1][p+i-1].first == mat[k+i-1][p+i-1].second) ++ret;}else if(p == 0){if(mat[k+i-1][p+i-1].first - mat[k-1][p+i-1].first == mat[k+i-1][p+i-1].second - mat[k-1][p+i-1].second ){ret++; }}else if( k == 0){if(mat[k+i-1][p+i-1].first - mat[k+i-1][p-1].first == mat[k+i-1][p+i-1].second - mat[k+i-1][p-1].second ){ret++; }}else {if(mat[k+i-1][p+i-1].first - mat[k+i-1][p-1].first - mat[k-1][p+i-1].first + mat[k-1][p-1].first == mat[k+i-1][p+i-1].second - mat[k+i-1][p-1].second - mat[k-1][p+i-1].second + mat[k-1][p-1].second){ret++; }}}}cout << ret << endl;}}return 0;
}
// 64 位输出请用 printf("%lld")
相关文章:

美团春招编程第一场第三题
美团春招编程第一场第三题 题目 解答 思路-暴力解法 pair中存储从原点到包含当前元素的0,1数量,得到二维数组mat; 从头到尾遍历尺寸为i*i的矩形,计算完美矩形数量 #include <iostream> #include <vector> using namespace std;int main()…...

BulingBuling - 《金钱心理学》 [ The Psychology of Money ]
金钱心理学 摩根-豪泽尔 关于财富、贪婪和幸福的永恒课程 The Psychology of Money Morgan Housel Timeless Lessons on Wealth, Greed, and Happiness 内容简介 [ 心理学 ] [ 金钱与投资 ] Whats it about? [ Psychology ] [ Money & Investments ] 《金钱心理学》&…...

急速建立网站方法
急速建立网站方法 WordPress: 简介: WordPress是一种广泛用于建设博客、网站的免费开源内容管理系统(CMS)。它具有友好的用户界面和丰富的插件生态系统,使得用户可以轻松创建和管理网站。特点: 主题和插件支…...
Java EE之wait和notify
一.多线程的执行顺序 由于多个线程执行是抢占式执行,就会导致顺序不同,同时就会导致出现问题,就比如俩个线程同时对同一个变量进行修改,我们难以预知执行顺序。 但在实际开发中,我们希望代码按一定的逻辑顺序执行&am…...
PostgreSQL中In, Exists在SQL查询中到底有无区别
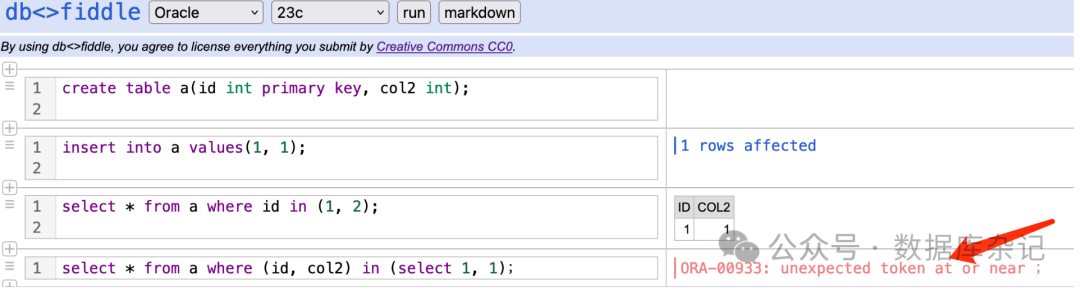
前言 SQL查询当中,In和Exists子查询到底有无区别?记得很多年以前,确实是有相关的使用戒条的,或者说存在一些使用的惯用法。试图完全抹开两者的区别,就有点过了。 两者的主要区别: 从目的上讲,…...

Netty Review - 探究Netty服务端主程序无异常退出的背后机制
文章目录 概述故障场景尝试改进问题分析铺垫: Daemon线程Netty服务端启动源码分析逻辑分析 如何避免Netty服务端意外退出最佳实践 概述 在使用Netty进行服务端程序开发时,初学者可能会遇到各种问题,其中之一就是服务端意外退出的问题。这种问…...
【兔子机器人】修改GO电机id(软件方法、硬件方法)
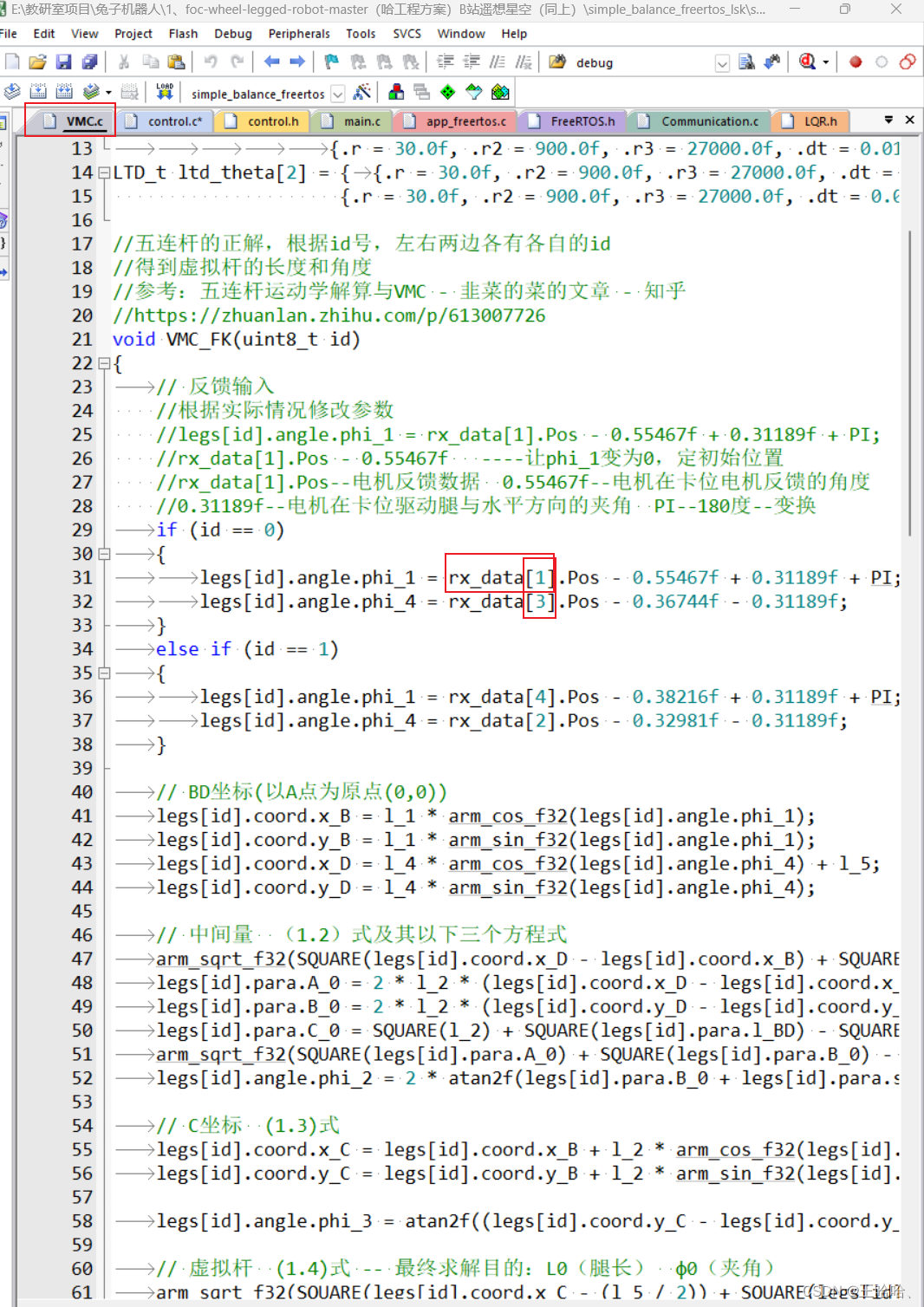
一、硬件方法 利用上位机直接修改GO电机的id号: 打开调试助手,点击“调试”,查询电机,修改id号,即可。 但先将四个GO电机连接线拔掉,不然会将连接的电机一并修改。 利用24V电源给GO电机供电。 二、软件方…...

Spring MVC | Spring MVC 的“核心类” 和 “注解”
目录: Spring MVC 的“核心类” 和 “注解” :1.DispatcherServlet (前端控制器)2.Controller 注解3.RequestMapping 注解3.1 RequestMapping 注解的 “使用”标注在 “方法” 上标注在 “类” 上 3.2 RequestMapping 注解的 “属性” 4.组合注解4.1 请求处理方法的…...
Python 创建PPT
本篇为如何使用Python来创建ppt文件。 创建PPT 安装必要的库 命令如下: pip install python-pptx 安装过程: 创建ppt文件 在当前目录下创建一个test的ppt文件。其中包含两页,分别使用了不同的布局。 第一页设置了标题和内容。第二页只设…...
【工具】Git的24种常用命令
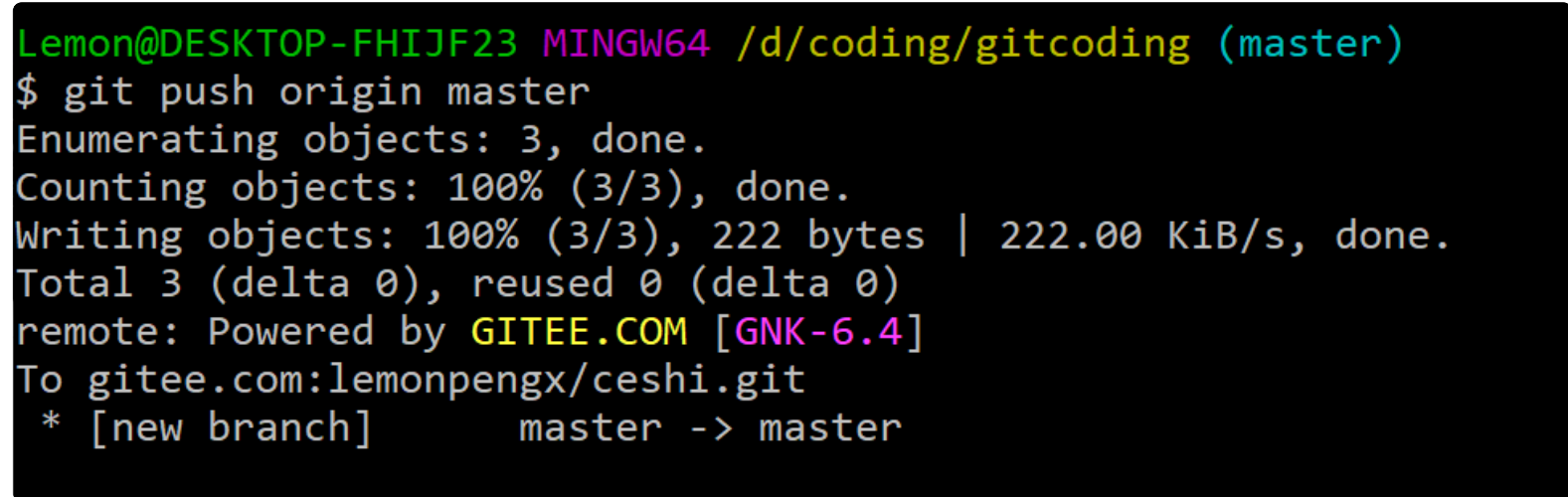
相关链接 传送门:>>>【工具】Git的介绍与安装<< 1.Git配置邮箱和用户 第一次使用Git软件,需要告诉Git软件你的名称和邮箱,否则无法将文件纳入到版本库中进行版本管理。 原因:多人协作时,不同的用户可…...
rabbitmq 基本总结
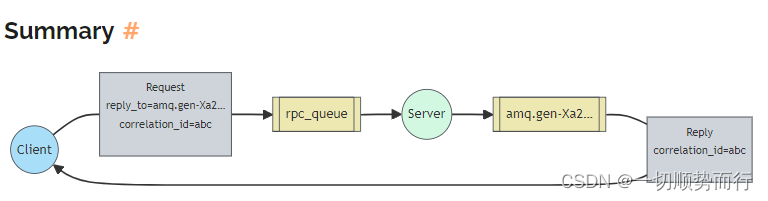
rabbitmq 的基本概念 vhost、broker、producer、 consumer、 exchange、 queue、 routing key rabbitmq 常用的队列类型,工作队列(简单队列),pub/sub, routing key, topic 模式 <dependency><groupId>com.rabbitmq&l…...

7、Copmose自定义颜色和主题切换
Copmose自定义颜色和主题切换 一起颜色的设置的都是在res/values/colors里面去做颜色, 但是当使用compose的时候,抛弃了使用了ui.theme底下的Color.kt和Theme.kt 但是默认使用的是MaterialTheme主题,里面的颜色字段不能定义,因此…...

js-判断变量是否定义
if (typeof myVar undefined) {// myVar (未定义) 或 (已定义但未初始化) } else {// myVar (已定义和已初始化) } 参考 https://www.cnblogs.com/redFeather/p/17662966.html...
视频远程监控平台EasyCVR集成后播放只有一帧画面的原因排查与解决
智慧安防视频监控平台EasyCVR能在复杂的网络环境中(专网、局域网、广域网、VPN、公网等)将前端海量的设备进行统一集中接入与视频汇聚管理,平台可支持的接入协议包括:国标GB28181、RTSP/Onvif、RTMP,以及厂家的私有协议…...

Pulsar 社区周报 | No.2024.03.08 Pulsar-Spark Connector 助力实时计算
关于 Apache Pulsar Apache Pulsar 是 Apache 软件基金会顶级项目,是下一代云原生分布式消息流平台,集消息、存储、轻量化函数式计算为一体,采用计算与存储分离架构设计,支持多租户、持久化存储、多机房跨区域数据复制,…...

Redis--线程模型详解
Redis线程模型 Redis内部使用的文件事件处理器(基于Reactor模式开发的)file event handler是单线程的,所以Redis线程模型才叫单线程模型,它采用IO多路复用机制同时监听多个socket,当被监听的socket准备好执行accep、r…...

[备赛笔记]——5G大唐杯(5G考试等级考考试基础试题)
个人名片: 🦁作者简介:学生 🐯个人主页:妄北y 🐧个人QQ:2061314755 🐻个人邮箱:2061314755qq.com 🦉个人WeChat:Vir2021GKBS 🐼本文由…...

【解读】OWASP 大语言模型(LLM)安全测评基准V1.0
大语言模型(LLM,Large Language Model)是指参数量巨大、能够处理海量数据的模型, 此类模型通常具有大规模的参数,使得它们能够处理更复杂的问题,并学习更广泛的知识。自2022 年以来,LLM技术在得到了广泛的应…...
java数据结构与算法刷题-----LeetCode77. 组合
java数据结构与算法刷题目录(剑指Offer、LeetCode、ACM)-----主目录-----持续更新(进不去说明我没写完):https://blog.csdn.net/grd_java/article/details/123063846 文章目录 1. 递归实现 解题思路 这种题只能暴力求解,枚举所有可…...
)
网络安全运营的工作内容(附资料下载)
【推荐】最新网络安全运营方案和实践合集(共80多份).zip 网络安全运营的工作内容是一个多层次、多维度的体系,涵盖了多个关键领域以确保网络环境的稳定和安全。以下是一些主要的工作内容: 安全策略制定与实施: 制定网…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...
