从零开始:神经网络(2)——MP模型
声明:本文章是根据网上资料,加上自己整理和理解而成,仅为记录自己学习的点点滴滴。可能有错误,欢迎大家指正。
神经元相关知识,详见从零开始:神经网络——神经元和梯度下降-CSDN博客
1、什么是M-P 模型
人脑中的神经网络是一个非常复杂的组织。成人的大脑中估计有1000亿个神经元之多。那么神经网络是如何实现这种模拟的,并且达到一个惊人的良好效果的?这要由“飞鸟派”即仿生派说起。仿生派就是把进化了几百万年的生物,作为“模仿”对象,搞清楚原理后,再复现这些对象的特征。其实现在所讲的神经网络包括深度学习,都在某种程度上,属于“飞鸟派”——它们在模拟大脑神经元的工作机理。追根溯源,模仿神经元的“飞鸟”实例,就是上世纪40年代提出但一直沿用至今的“M-P神经元模型”。
1943年,由美国心理学家麦卡洛克(McCulloch, W. S. )和数学家皮特斯((Puts , W.) 按照生物神经元,建立起了著名的阈值加权和模型,即麦卡洛克-皮特斯模型(McCulloch-Pitts model),简称为M-P模型,其拓扑结构便是现代神经网络中的一个神经元。
在这个模型中,神经元接收来自n个其它神经元传递过来的输入信号x(图中~
),这些信号的表达,通常通过神经元之间连接的权重w(图中
~
)大小来表示,神经元将接收到的输入值按照某种权重叠加起来,并将当前神经元的阈值θ进行比较,然后通过“激活函数(activation function)”f()向外表达输出,如图所示。
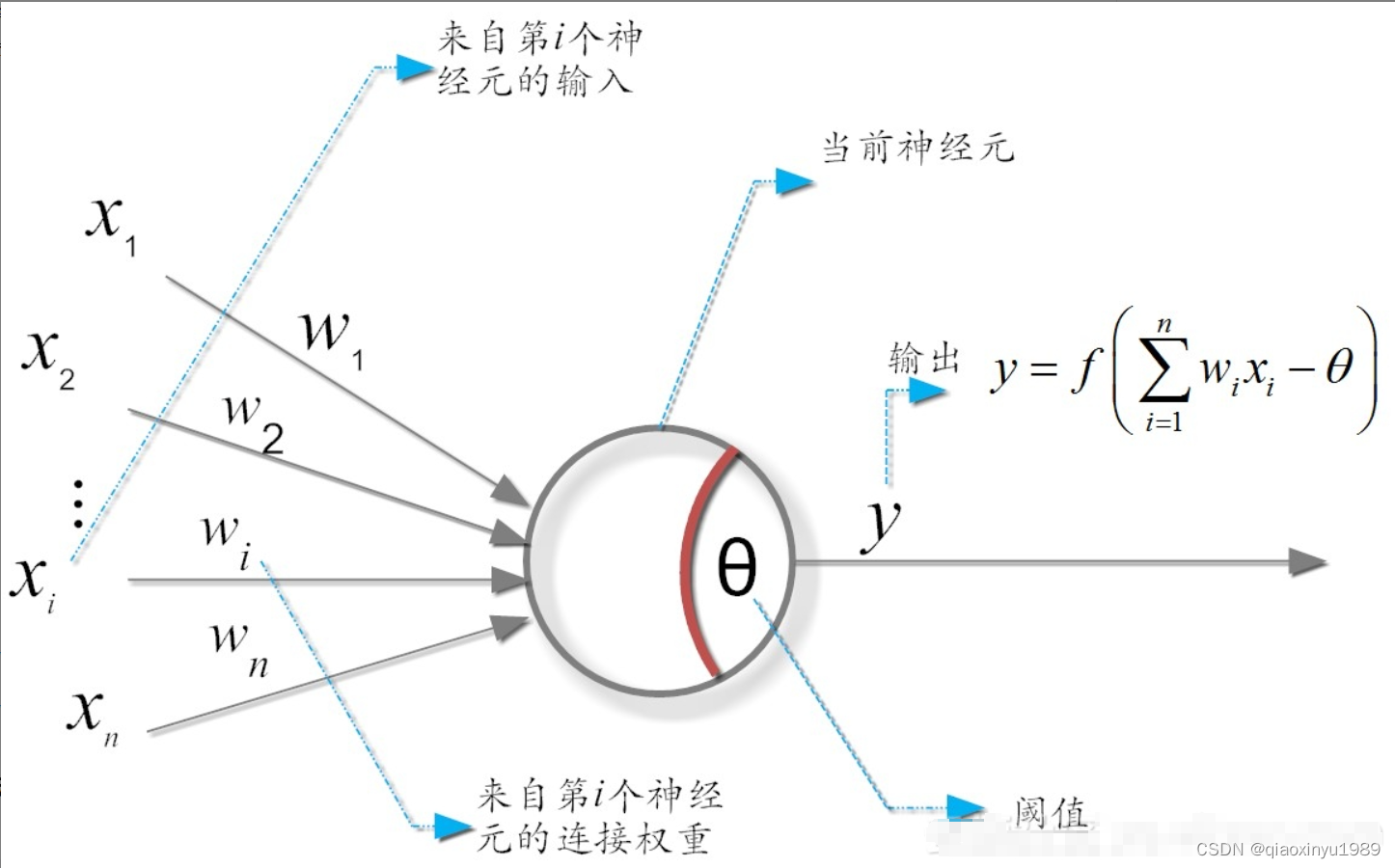
即
M-P模型的工作原理为:当所有的输入与对应的连接权重的乘积大于阈值
时,y输出为1,否则输出为0。即当
,
;否则
需要注意的是,
也只能是0或1的值,而权重
和
则根据需要自行设置。
简单吧?很简单!但是还是看不懂,下面举例说明
2、M-P数学表达式
如下图所示,假设某个模型:包含有3个输入,1个输出,以及2个计算功能。注意中间的箭头线。这些线称为“连接”(神经元中最重要的东西)。每个上有一个“权值”。
一个神经网络的训练算法就是让权重的值调整到最佳,以使得整个网络的预测效果最好。
举个例子,如果我们已知张三,李四重多少,想让神经网络输出两个人受到的重力加在一起是多少。我们其实知道关于重力的公式 ,但是这个单层神经网络并不知道,那么怎么让他学习到这个关系呢?假设我们统计了很多个数据(输入),每个数据包含第一个人重
kg,第二个人的重
kg,以及他们一起的重力
(输出)。我们将这些数据丢给神经网络去学习,它最终会学习(调整)两个参数
,
(权值),逼近于
的值。所以可以用这个数学公式来表示:
但此时,神经网络还只能做到线性的变换。但是其实在现实生活中很多问题,输入和输出不是线性的关系的。 比如一个狗狗图片,我们人眼看到它,大脑会分辨出这是一只狗。其中狗狗图片就是输入,这是一只狗是输出,其中大脑处理的过程肯定不是线性的变换。那怎么办?
神经网络通过激活函数(也就是上图的非线性函数)来实现了这个非线性变换。你可能会问一个激活函数就有这么大的作用吗?就好比0和1一样,基于它们才有了我们现在的计算机,它甚至构造了整个虚拟世界。同样,如果有多个单层神经元组合起来,再加上可学习的参数调整,它能做的事情会很多,甚至出乎你的意料。最终上面的数学公式变成了:
下面,我们使用a来表示输入,用w来表示权值。一个表示连接的有向箭头可以这样理解:在初端,传递的信号大小仍然是a,端中间有加权参数w,经过这个加权后的信号会变成a*w,因此在连接的末端,信号的大小就变成了a*w。如果我们将神经元图中的所有变量用符号表示,并且写出输出的计算公式的话,就是下图:
可见z是在输入和权值的线性加权和叠加了一个函数g的值。在M-P模型里,函数g是sgn函数(sgn是英文sign(标记)的缩写),即符号函数(sign function)。这个函数当输入大于0时,输出1,否则输出0。即

下面对神经元模型的图进行一些扩展。首先将sum函数与sgn函数合并到一个圆圈里,代表神经元的内部计算。其次,把输入a与输出z写到连接线的左上方,便于后面画复杂的网络。最后说明,一个神经元可以引出多个代表输出的有向箭头,但值都是一样的。神经元可以看作一个计算与存储单元。计算是神经元对其的输入进行计算功能。存储是神经元会暂存计算结果,并传递到下一层。
当我们用“神经元”组成网络以后,描述网络中的某个“神经元”时,我们更多地会用“单元”(unit)来指代。同时由于神经网络的表现形式是一个有向图,有时也会用“节点”(node)来表达同样的意思。
需要说明的是,至今为止,我们对神经网络的结构图的讨论中都没有提到偏置节点(bias unit)。事实上,这些节点是默认存在的。它本质上是一个只含有存储功能,且存储值永远为1的单元(即相当于输入a0=1,如下图中的+1)。在神经网络的每个层次中,除了输出层以外,都会含有这样一个偏置单元。那么,为什么要存在偏置呢?
从生物学上解释,在脑神经细胞中,一定是输入信号的电平/电流大于某个临界值(阈值)时,神经元细胞才会处于兴奋状态,即当:
时,该神经元细胞才会兴奋。我们把挪到等式左侧来,变成
,然后把它写成 b ,变成了:
于是偏置 b就诞生了!亦即,我们可以得到神经元的数学/计算模型如下所示:
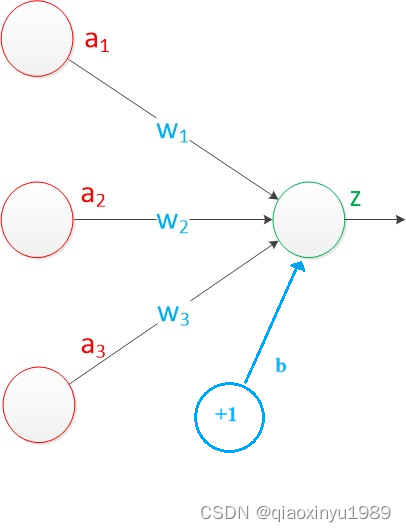
可以看出,偏置节点很好认,因为其没有输入(前一层中没有箭头指向它)。有些神经网络的结构图中会把偏置节点明显画出来,有些不会。一般情况下,我们都不会明确画出偏置节点。
在考虑了偏置以后上图的神经网络的矩阵运算为:
(1)单个神经元的MP数学公式
则单个神经元的MP模型为:
其中,输入:表示第 i个输入变量(自变量),m为输入变量的个数
输入:表示第 i个权重,与相同下标的
相对应
输入 表示偏置
输出 表示输出变量(因变量)
表示一个激活函数,它对线性加权求和的结果进行非线性变换
把矩阵上的输入(实数值向量)映射到输出值上(一个二元值),其数学表达式为:
式子(1)
(2)单个神经元的MP数学公式
如果将多个神经元的MP模型统一编号,可以表示成一个式子:
其中,输入:表示第 i个输入变量(自变量),m为输入变量的个数
输入:表示第
个神经元的第 i个权重
输入 表示第
个神经元的偏置
输出 表示第
个神经元的输出变量(因变量)
n表示神经元的个数
3、M-P模型逻辑规则的应用
(1)非运算
非运算是单输入和单输出,结构图如下:
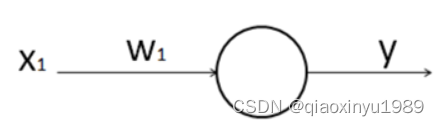
则其表达式为:
运算原理:
| 代入求值的x= | 根据sgn(x)的规则(见式子1), 可得偏置b取值范围 | |||
| 0 | 1 | 即: | ||
| 1 | 0 | |||
如:可取,均满足b的取值范围,则
(2)或运算
或运算以两个输入为例,结构图如下:
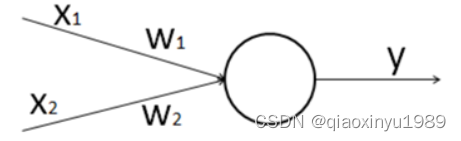
则其表达式为:
运算原理:
| 代入求x的值 | 根据sgn(x)的规则(见式子1), 可得偏置b取值范围 | ||||
| 0 | 0 | 0 | |||
| 0 | 1 | 1 | |||
| 1 | 0 | 1 | |||
| 1 | 1 | 1 | |||
如:可取,均满足b的取值范围,则
(3)与运算
逻辑与运算与逻辑或一致,把运算原理改改即可:
运算原理:
| 代入求x的值 | 根据sgn(x)的规则(见式子1), 可得偏置b取值范围 | ||||
| 0 | 0 | 0 | |||
| 0 | 1 | 0 | |||
| 1 | 0 | 0 | |||
| 1 | 1 | 1 | |||
如:可取,均满足b的取值范围,则
(4)异或运算(不能实现)
仍然以二输入为例:表达式为:
运算原理:
| 代入求x的值 | 根据sgn(x)的规则(见式子1), 可得偏置b取值范围 | ||||
| 0 | 0 | 0 | 因为既要大于 | ||
| 0 | 1 | 1 | |||
| 1 | 0 | 1 | |||
| 1 | 1 | 0 | |||
如:可取,均满足b的取值范围,则
4、实例
M-P模型可以实现逻辑非、或和与运算,但是当时还没有通过对训练样本进行训练来确定参数的方法,上述参数如权重参数和阈值只能人为事先计算后确定。这里没有具体的代码噢!!!
该篇文章的目的,主要是让你明白M-P模型的计算公式,以及激活函数的取值为0-1折线型。
熟悉M-P模型在逻辑运算中的应用,体验人为添加权重和阈值,实现逻辑运算。其实,在之后的感知器(机)也是在这个神经元模型基础上去延伸发展的,使得神经网络的发展得到有效的突破。
相关文章:
从零开始:神经网络(2)——MP模型
声明:本文章是根据网上资料,加上自己整理和理解而成,仅为记录自己学习的点点滴滴。可能有错误,欢迎大家指正。 神经元相关知识,详见从零开始:神经网络——神经元和梯度下降-CSDN博客 1、什么是M-P 模型 人…...
Python调用edge-tts实现在线文字转语音
edge-tts是一个 Python 模块,允许通过Python代码或命令的方式使用 Microsoft Edge 的在线文本转语音服务。 项目源码 GitHub - rany2/edge-tts: Use Microsoft Edges online text-to-speech service from Python WITHOUT needing Microsoft Edge or Windows or an…...

植物病害识别:YOLO甘蔗叶片病害识别分类数据集
YOLO甘蔗叶片病害识别数据集, 包含尾孢菌叶斑病,眼斑病,健康,红腐病,锈病,黄叶病6个常见病类别,3300多张图像,yolo标注完整,全部原始图像,未应用增强。 适用于CV项目&…...

pyqt QTextEdit 捕获enter按键
参考: https://blog.csdn.net/qq_27061049/article/details/101550616 方法一: 在PyQt中,可以通过重写QTextEdit的keyPressEvent()函数来捕获Enter按键。下面是示例代码: from PyQt5.QtWidgets import QApplication, QMainWindo…...
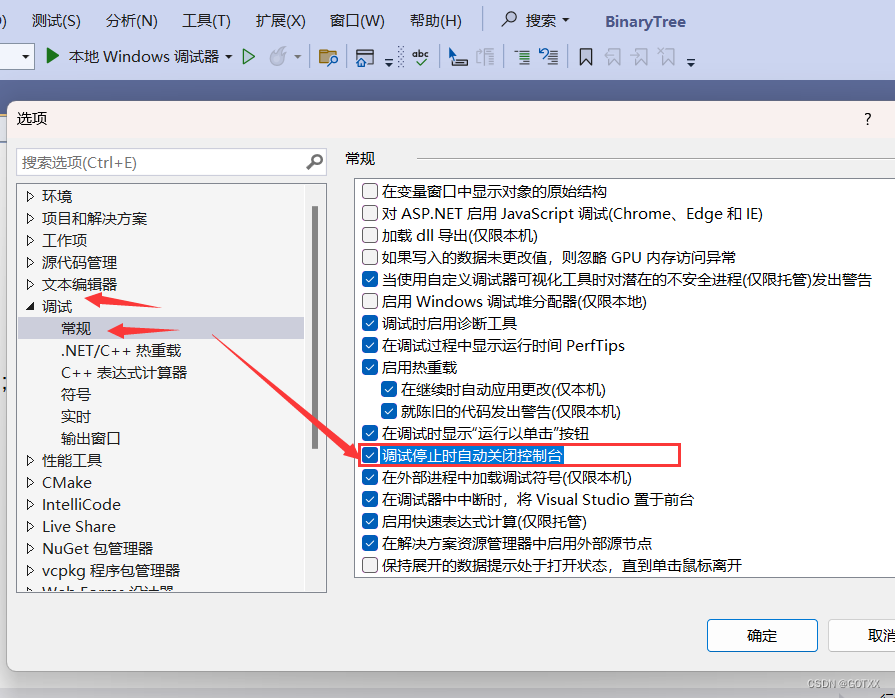
一劳永逸的方法解决:LNK1168无法打开 xxx.exe 进行写入 报错问题
这种错误的产生原因: 运行程序退出不是按正常流退出,是按窗口右上角的 “X” 来关闭程序,但是后台的xxx.exe控制台程序还在运行;修改程序的代码后再运行,就会报LNK1168的错误; 报错示例: 解决方…...

程序员的金三银四求职宝典:面试技巧分享
随着春天的到来,程序员们迎来了求职的旺季——金三银四。在这个时期,各大公司纷纷开放招聘,为求职者提供了丰富的选择机会。然而,如何在众多的面试中脱颖而出,成功获得心仪的职位,就需要掌握一些有效的面试技巧。下面,就让我们一起来探讨一下金三银四求职…...
)
【DevOps基础篇之k8s】如何应用Kubernetes中的Role Based Access Control(RBAC)
【DevOps基础篇之k8s】如何应用Kubernetes中的Role Based Access Control(RBAC) 目录 【DevOps基础篇之k8s】如何应用Kubernetes中的Role Based Access Control(RBAC)背景Kubernetes身份验证和授权基于角色的访问控制(RBAC)用户账户 vs. 服务账户角色 vs. 集群角色RoleBi…...
)
python知网爬虫论文pdf下载+立即可用(动态爬虫)
文章目录 使用代码 使用 自己工作需要,分享出来,刚刚修改完。 知需要修改keyword就可以完成自动搜索和下载同时翻页。 但是需要安装Chrome,也支持linux爬虫,也要安装linux Chrome非可视化版。 代码 import selenium.webdriver …...

DataFunSummit 2023:洞察现代数据栈技术的创新与发展(附大会核心PPT下载)
随着数字化浪潮的推进,数据已成为企业竞争的核心要素。为了应对日益增长的数据挑战,现代数据栈技术日益受到业界的关注。DataFunSummit 2023年现代数据栈技术峰会正是在这样的背景下应运而生,汇聚了全球数据领域的精英,共同探讨现…...

运行 Jmeter 文件生成 HTML 测试报告,我选择 ANT 工具
概述 ant 是一个将软件编译、测试、部署等步骤联系在一起加以自动化的一个工具,大多用于 Java 环境中的软件开发。 在与 Jmeter 生成的 jmx 文件配合使用中,ant 会完成jmx计划的执行和生成jtl文件,并将jtl文件转化为html页面进行查看。 还可…...
TensorRT是什么,有什么作用,如何使用
TensorRT 是由 NVIDIA 提供的一个高性能深度学习推理(inference)引擎。它专为生产环境中的部署而设计,用于提高在 NVIDIA GPU 上运行的深度学习模型的推理速度和效率。以下是关于 TensorRT 的详细介绍: TensorRT 是 NVIDIA 推出的…...

同比和环比
1.同比就是今年的某时期与去年这个时期 进行对比 (消除季节性差异) 例子:2018年一季度销量 2019年一季度销量 上升/下滑 2.环比是今年的某个时期与当前上一个时期进行对比(两个时期是连续的) 例子:2024年1月 营收额1000万元 2024年2月营收额3000万元 同比增长...

js中批量修改对象属性
首先,有这个对象 let a {id: 1,name: 张三,age: 18,sex: 0 }需求:同时修改name,id,并添加一个新属性c 常规写法: a.id 2; a.name 李四; a.c 1;但这种写法遇到批量就会很麻烦 解决方法: 方法1: 使用Object.assi…...

应用案例 | Softing echocollect e网关助力汽车零部件制造商构建企业数据库,提升生产效率和质量
为了提高生产质量和效率,某知名汽车零部件制造商采用了Softing echocollect e多协议数据采集网关——从机器和设备中获取相关数据,并直接将数据存储在中央SQL数据库系统中用于分析处理,从而实现了持续监控和生产过程的改进。 一 背景 该企业…...

使用大带宽服务器对网站有什么好处?
近年来大带宽服务器频频出现在咱们的视野当中,选用的用户也在与日增长。那么究其主要原因是什么?租用大带宽服务器的好处又有哪些? 今天德迅云安全带您来了解下。1.有效提升网站访问速度 一般来说,正规的网站对用户体验度都是非常有讲究的,…...
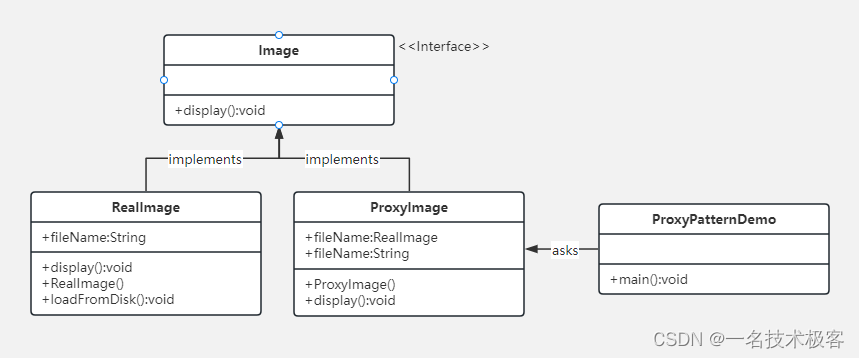
17-Java解释器模式 ( Interpreter Pattern )
Java解释器模式 摘要实现范例 解释器模式(Interpreter Pattern)实现了一个表达式接口,该接口解释一个特定的上下文 这种模式被用在 SQL 解析、符号处理引擎等 解释器模式提供了评估语言的语法或表达式的方式,它属于行为型模式 …...
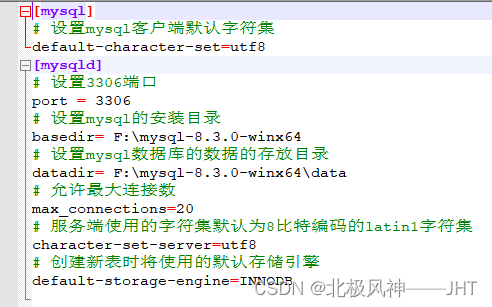
mysql的安装启动
下载 2.解压后放在某个目录下: 3.修改系统变量 4.修改配置文件 (创建一个ini文件放在解压后的目录下) 内容如下 5.初始化mysql 1.用管理员模式下输入: mysqld --initialize --console C:\WINDOWS\system32>mysqld --initia…...
[Java安全入门]三.CC1链
1.前言 Apache Commons Collections是一个扩展了Java标准库里的Collection结构的第三方基础库,它提供了很多强大的数据结构类型和实现了各种集合工具类。Commons Collections触发反序列化漏洞构造的链叫做cc链,构造方式多种,这里先学习cc1链…...

为什么虚拟dom比真实dom更快
虚拟DOM(Virtual DOM)之所以在某些情况下比直接操作真实DOM更快,主要有以下几个原因: 批量更新:虚拟DOM可以将多个DOM操作批量更新为一次操作。当需要对真实DOM进行多次修改时,直接操作真实DOM会导致浏览器…...

力扣---腐烂的橘子
题目: bfs思路: 感觉bfs还是很容易想到的,首先定义一个双端队列(队列也是可以的~),如果值为2,则入队列,我这里将队列中的元素定义为pair<int,int>。第一个int记录在数组中的位…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...
