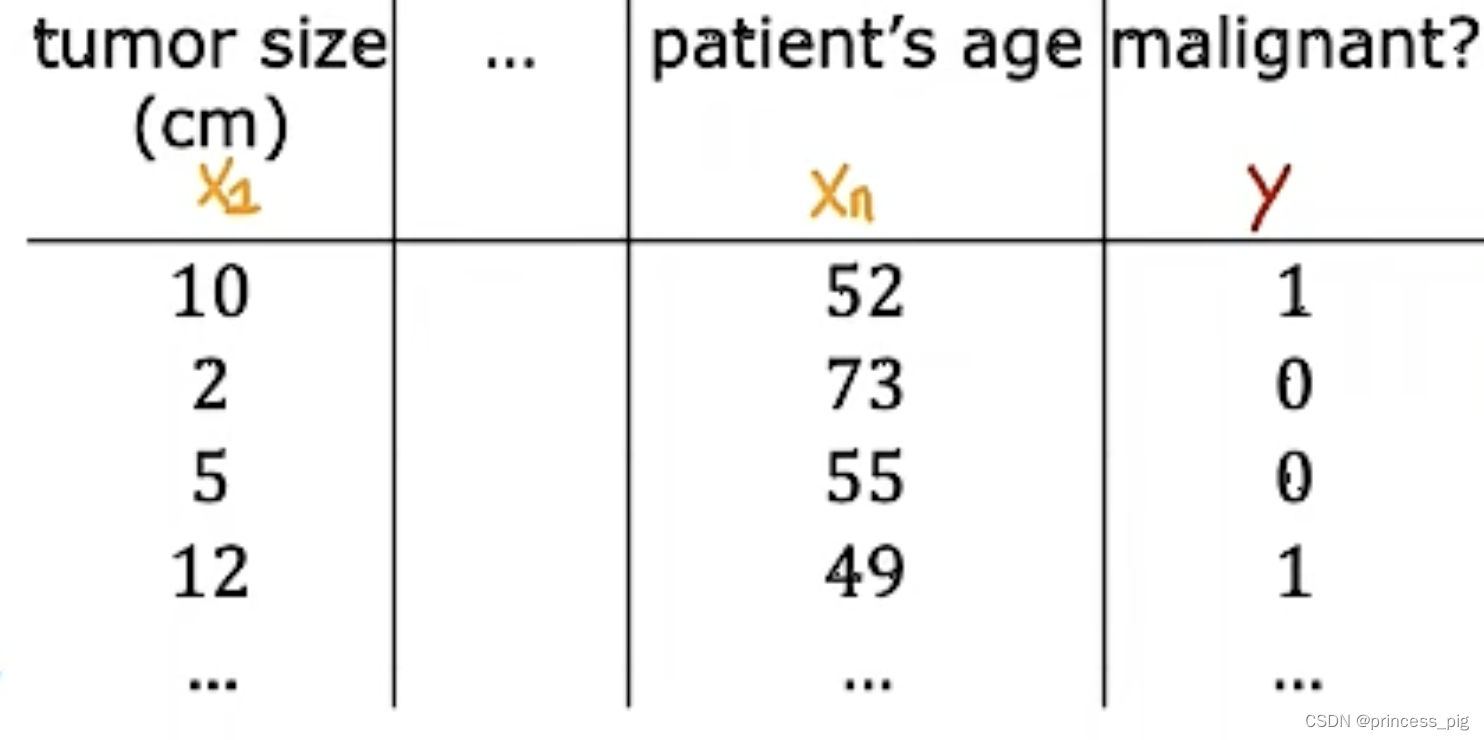
分类算法(Classification algorithms)
逻辑回归(logical regression):
逻辑回归这个名字听上去好像应该是回归算法的,但其实这个名字只是在历史上取名有点区别,但实际上它是一个完全属于是分类算法的。
我们为什么要学习它呢?在用我们的线性回归时会遇到一个很大的问题,就比如一下的图形。
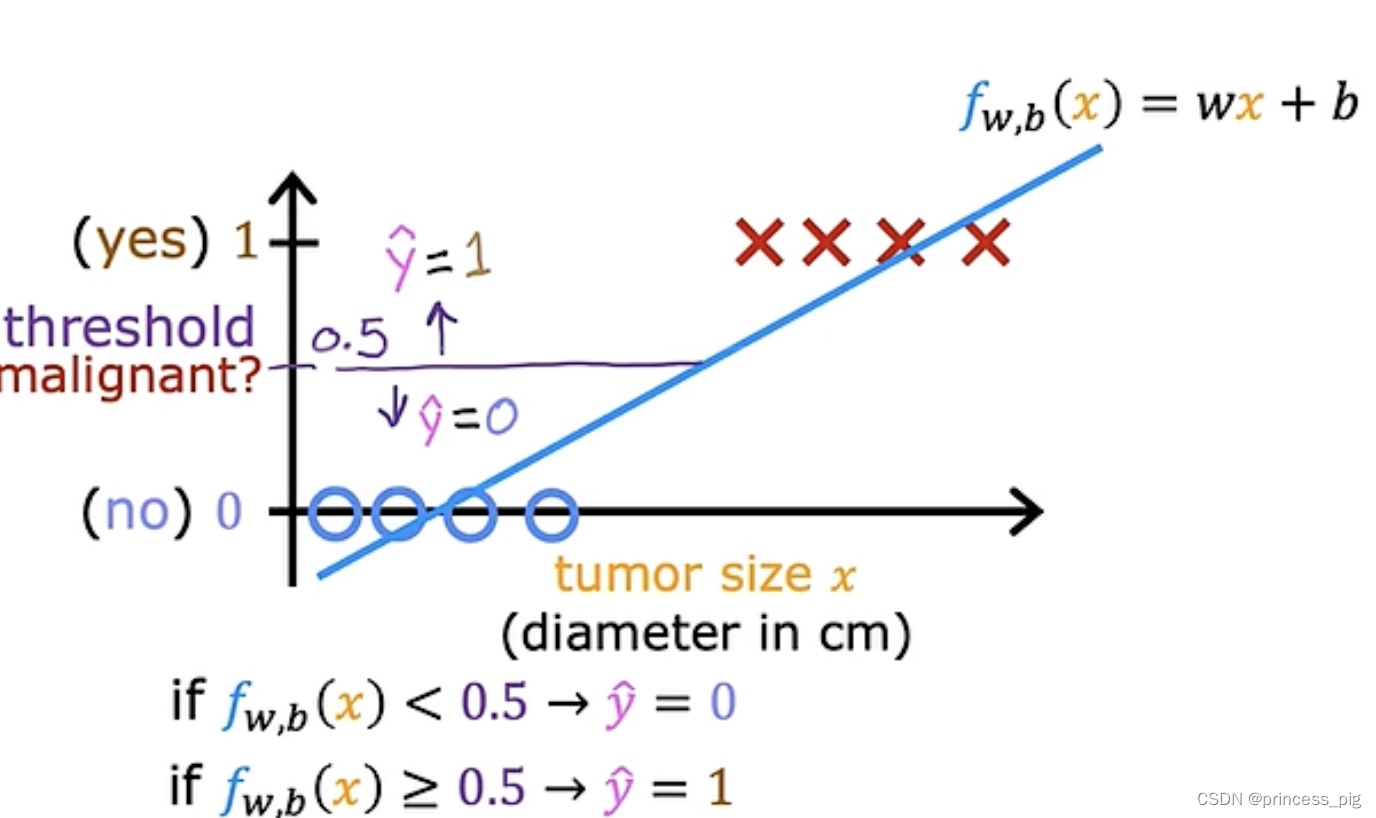
在这里我们把以上的图形进行了我们的线性回归得到了在0.5纵坐标的分界线,在0.5左侧是我们的良性肿瘤而在右边是我们的恶性肿瘤,这时我们得到了我们判断是否是良性肿瘤的方法,但当我们再添加一个数据时。
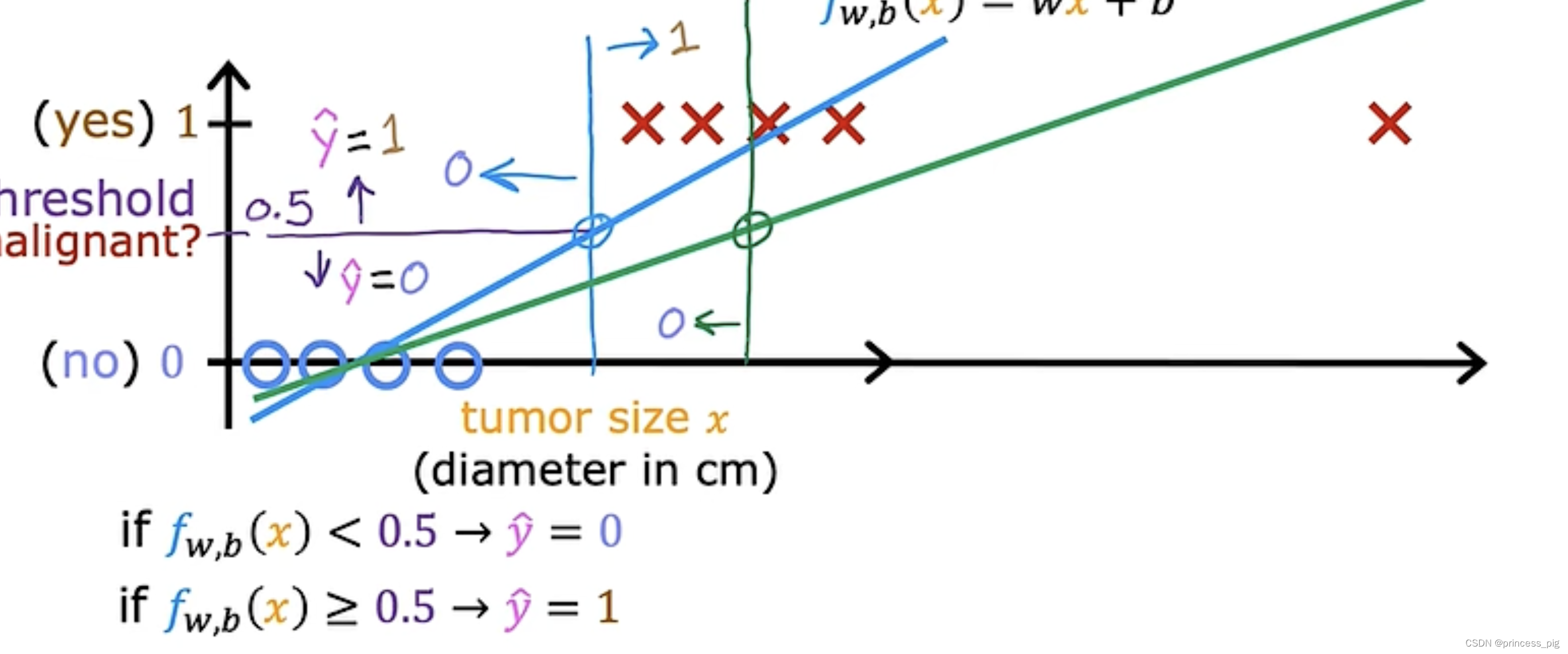
我们会发现我们的线性回归往右边平移了,而判断是否为良性肿瘤的值也往右边移动了,这时我们的模型就会因为我们的数据而发生变化,这很明显不是一个准确的方法,让我们得到我们需要的数据。所以我们需要学习一种叫做逻辑回归的算法。
逻辑函数(sigmoid function)
所以我们要创建一种新的函数。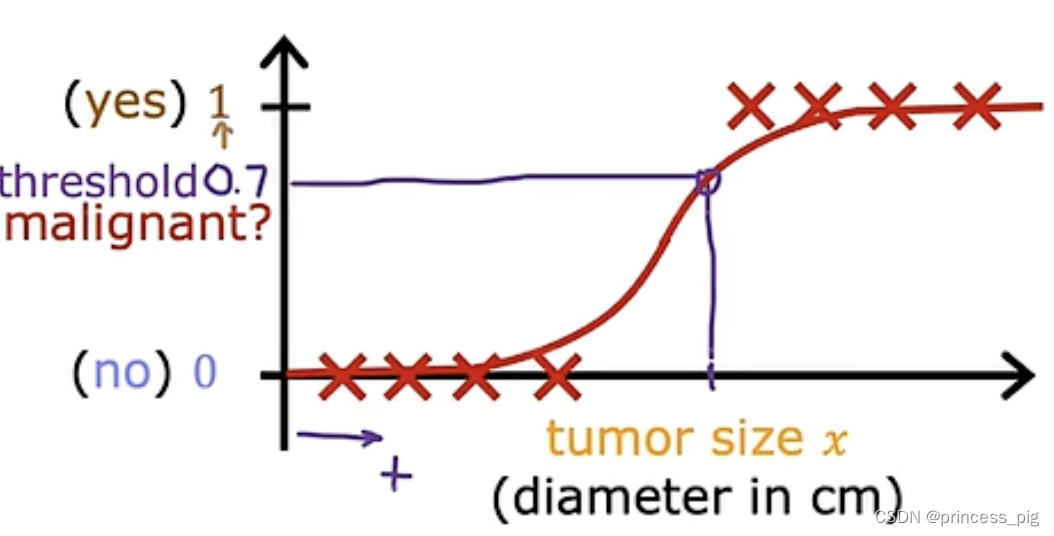
这里我们使用了sigmoid函数, 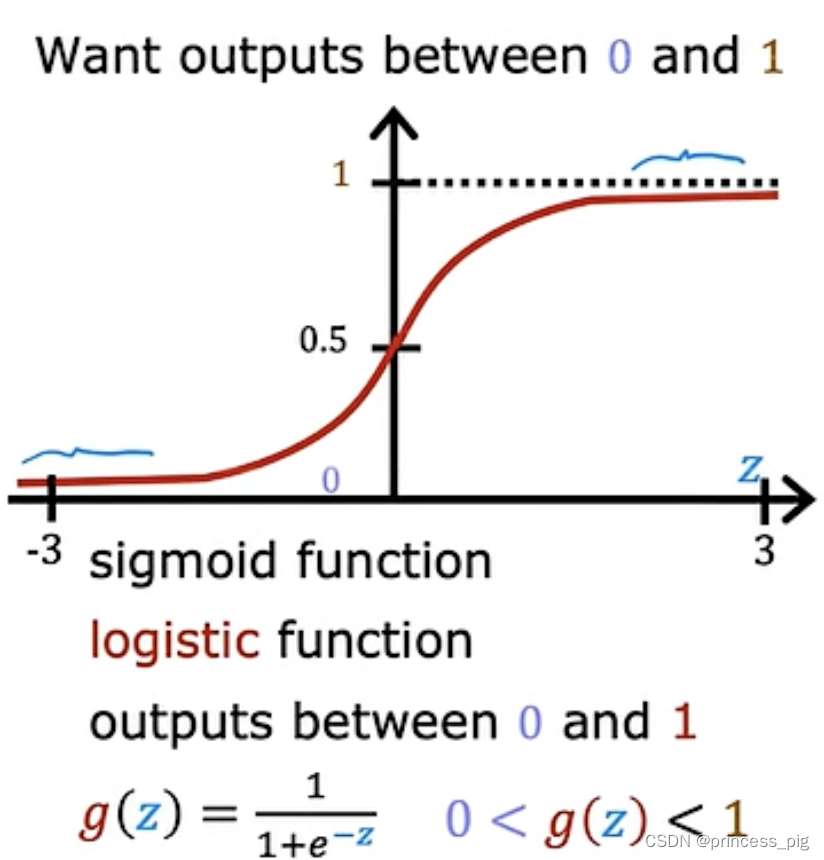
可以看到我们这个函数,,它所得到的函数可以是我们上图所示的样子。(可以自己手动画一下)在无限接近正无穷的地方它还是在缓慢的上升,而在负无穷处它则是无限接近于0。
那我们如何才能写一个逻辑回归函数呢?
第一步:我们的回归函数是,它的具体写法是
.。
第二步:我们sigmoid函数是。
第三步:我们把第一个式子代入,也就变成了。
我们解释一下我们得到的函数,在原来函数中我们知道它的y值在0到1,所以我们输入的x总会得到我们的一个值,而这个值一定在0和1之间,举一个例子。就那我们的判断肿瘤是否是恶性的例子,当我们的值为1时,则肿瘤为恶性肿瘤,当我们的值为0时,则它为良性肿瘤,当我们代入一个值时,y值输出为0.7,那么它就表示你有70%的概率会是恶性肿瘤。那为良性肿瘤的概率则为我们的30%。
这里有几个写法需要我们注意:1.,它指的是我们为1和为0的概率加起来为100%。2.
,它代表的意思就是我们的y=1时,我们的概率,而这里的w,b他们代表的只是它们对我们的答案会造成影响。
决策边界(Decision Boundary):
简单来说我们的决策边界就是当我们的逻辑函数曲线,在y值等于0.5时,也就是我们的z=0时,我们可以看看这个图。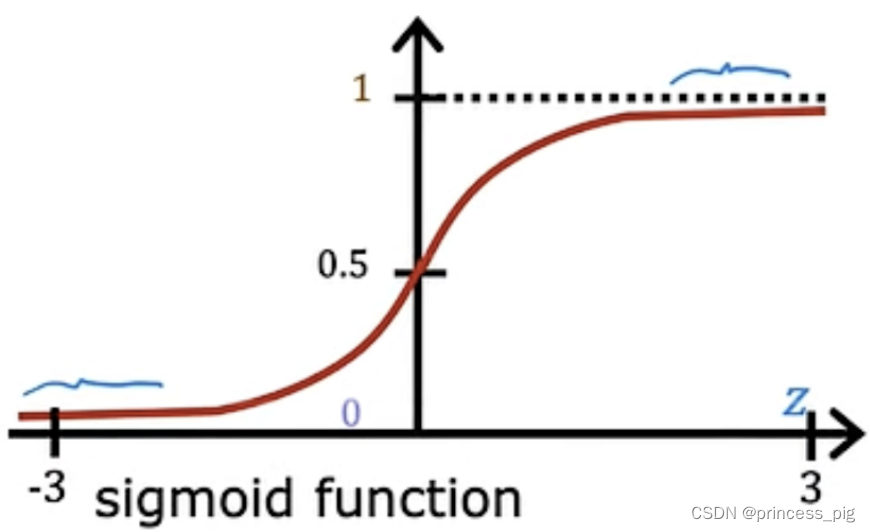
也就是 。我们举一个例子。比如得到了以下的图形。
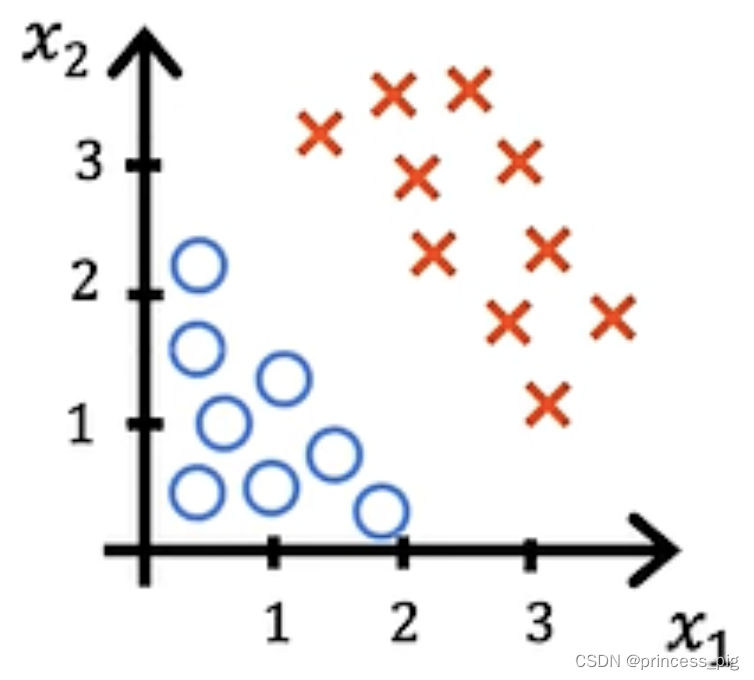 在图中我们的❌指的是我们的好的事物,而⭕️指的是坏的事物,这时,我们要找到我们的决策分界线。
在图中我们的❌指的是我们的好的事物,而⭕️指的是坏的事物,这时,我们要找到我们的决策分界线。
我们得到的数据是,这时我们假设我们的w1=1,w2=1,b=-3。这时我们得到的决策函数也就是
,这时我们就可以画出完美的决策边界。
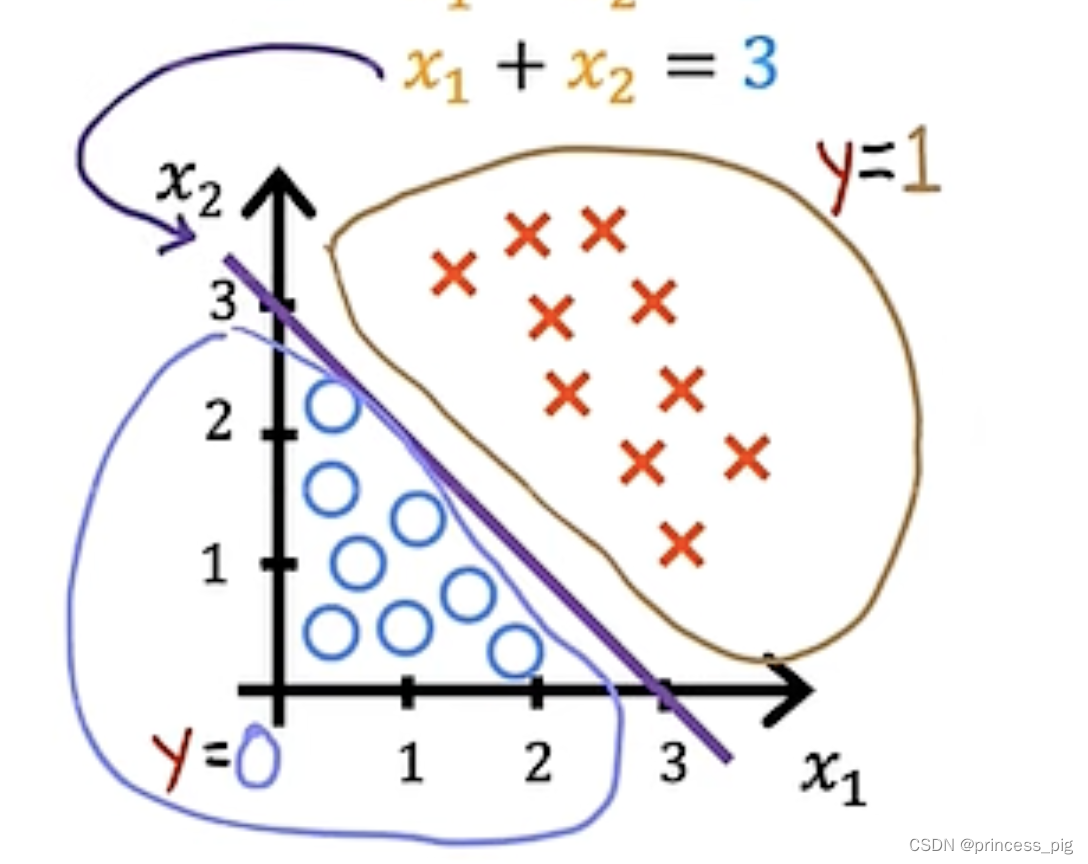
在上面就是我们的好事物,下面就是坏事物。这里有一个要强调,我们一般把0.5以上的看作是1,把0.5以下的看作成0。
当然也有多项式的情况,比如下图。
逻辑函数的成本函数(cost function):
在这个例子里面,我们的判断是否是一个良性肿瘤需要多组训练集,这里在前面几个特征与线性回归类似,而最后一个判断是否是良性或恶性用的是1和0来表示。
我们用原来的线性回归中,使用的成本函数,我们得到的图形将是。凹凸不平的,这让我们用梯度下降时只能取到我们的局部最小值,而不能得到我们的全局最小值。
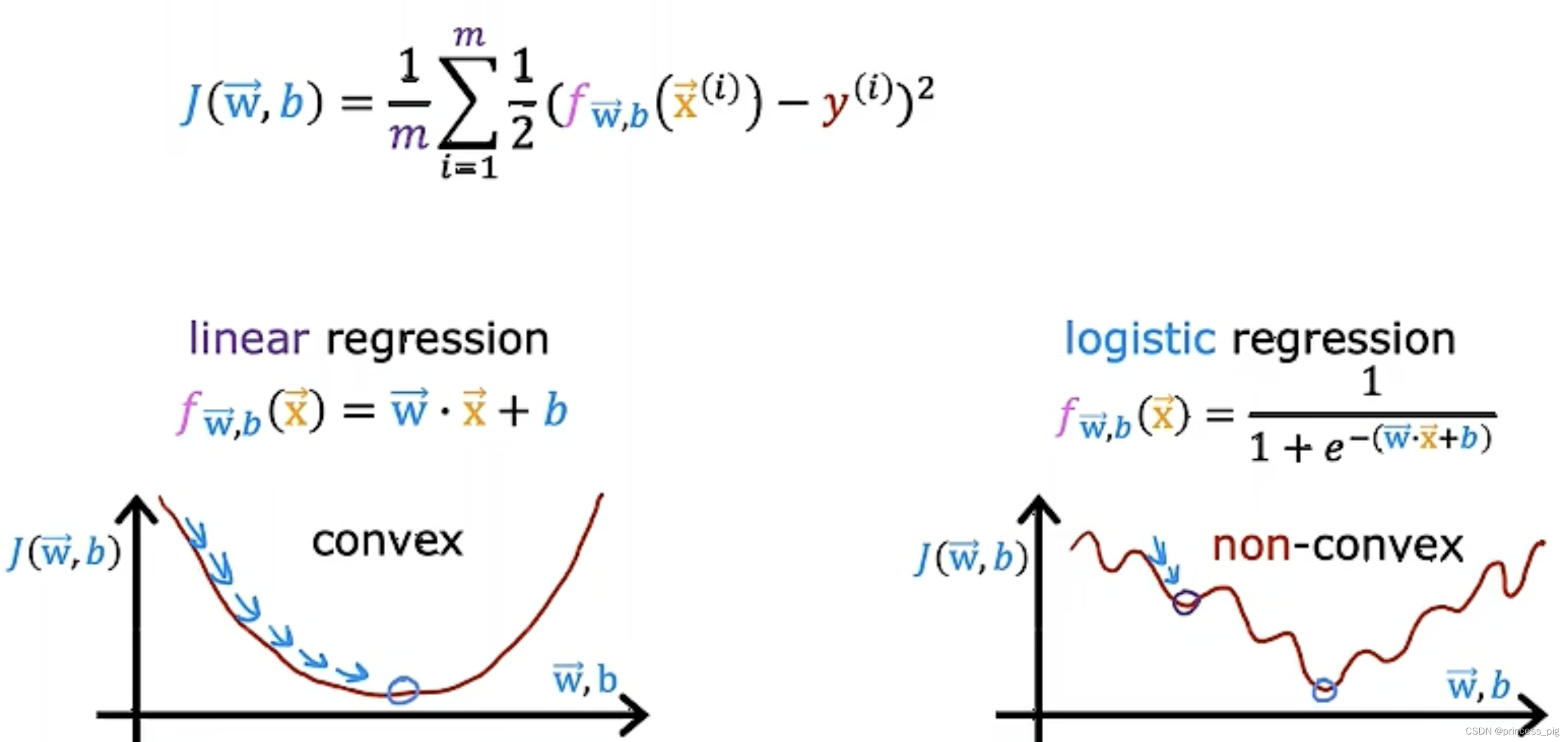
所以我们要用一个不一样的成本函数。
我们得到了一个新的成本函数:L() ,它的值和
相同,这个比较难推导,可以自己试一下(不建议)。
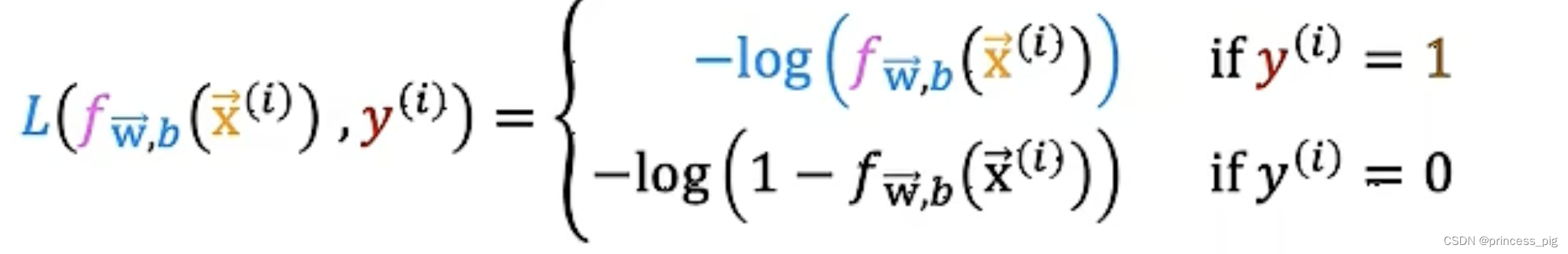
这时我们会得到两个对数函数,我们会在1和0时用到不同的函数去进行计算。
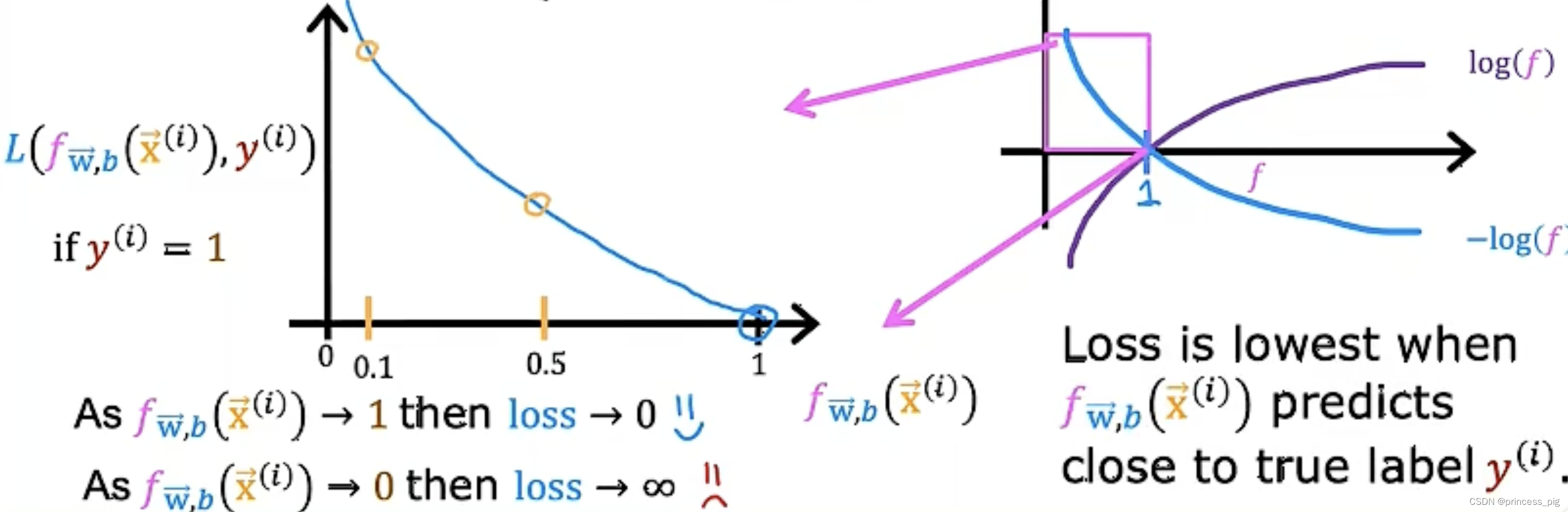
我们先看上面那一个方程,我们会发现预测的值越接近于1我们的损失就会越小,而我们接近于0的损失就会变大。同样的道理对于下面拿个方程。 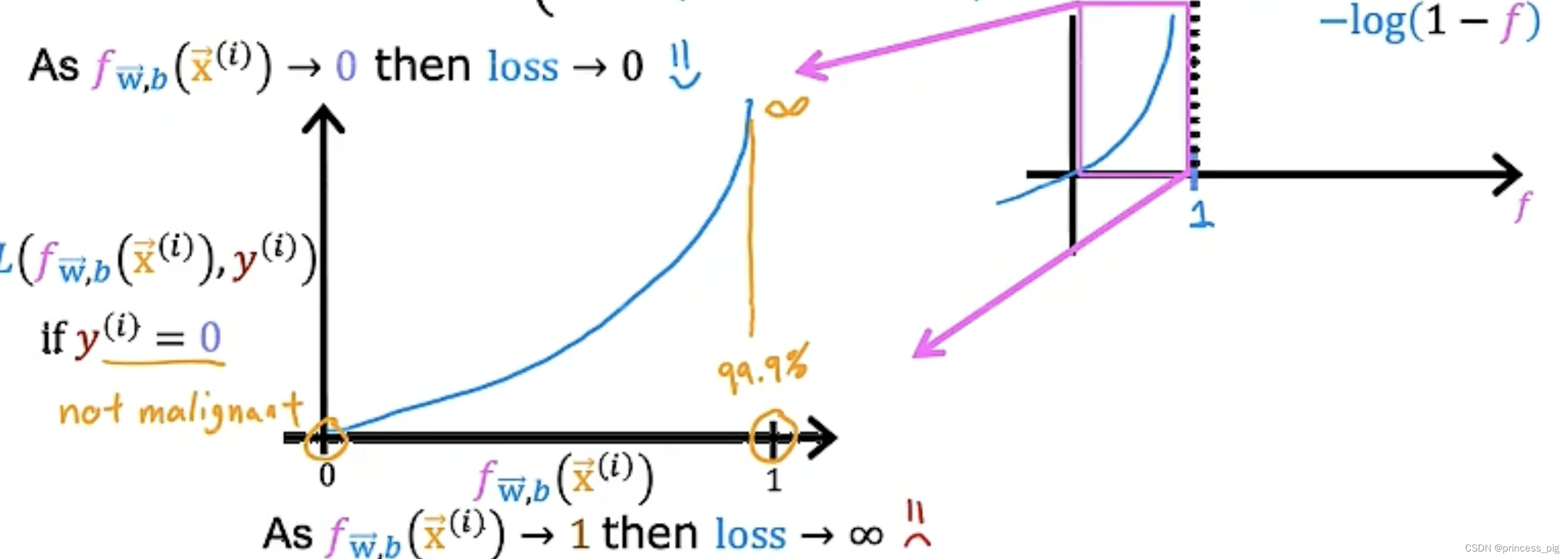
这里的损失函数,每一个都是一个单独的训练项,而不是一个集合。所以在这里的完整的成本函数写法是:
因为在这里我们的不是1就是0,所以我们可以简化我们的式子,那么它就变成了:
很明显它与我们在上面的式子是等价的。它是一种叫做最大似然估计的统计原理。
逻辑回归的梯度下降(gradient descent for logical regression):
在我们得到了我们的成本函数,接下来我们就要进行我们的梯度下降,还是一样的公式。
得到了我们的成本函数的式子:
然后我们还是用相同的方法进行我们的梯度下降。
和
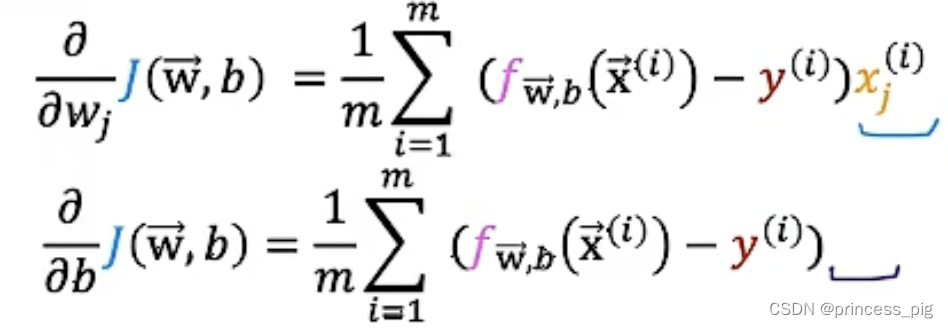
同样的道理,在这里的w,b的值是同时进行改变的,而没有先后的关系。两个偏导数算完之后我们才可以得到我们在上面的两个我们需要的特征值。
上面这个式子似乎和我们一开始在线性回归中用到的函数似乎是一样的但其实我们的f函数是完全不一样的,我们在我们的线性回归中,我们的函数是:,而在我们的逻辑回归中我们的函数是sigmoid函数(逻辑函数)。只是在我们算我们的梯度下降时我们用到的公式相同罢了。
相关文章:
分类算法(Classification algorithms)
逻辑回归(logical regression): 逻辑回归这个名字听上去好像应该是回归算法的,但其实这个名字只是在历史上取名有点区别,但实际上它是一个完全属于是分类算法的。 我们为什么要学习它呢?在用我们的线性回归时会遇到一…...

深度学习-Softmax 回归 + 损失函数 + 图片分类数据集
Softmax 回归 损失函数 图片分类数据集 1 softmax2 损失函数1均方L1LossHuber Loss 3 图像分类数据集4 softmax回归的从零开始实现 1 softmax Softmax是一个常用于机器学习和深度学习中的激活函数。它通常用于多分类问题,将一个实数向量转换为概率分布。Softmax函…...
)
分布式锁从0到1落地实现01(mysql/redis/zk)
1 准备数据库表 CREATE TABLE user ( id bigint(20) NOT NULL COMMENT 主键ID, name varchar(30) DEFAULT NULL COMMENT 姓名, age int(11) DEFAULT NULL COMMENT 年龄, email varchar(50) DEFAULT NULL COMMENT 邮箱, PRIMARY KEY (id) ) ENGINEInnoDB DEFAULT CHARSETutf8;I…...

安全运营方案的基本框架和关键要素
一、前言 阐述安全运营方案的目的和重要性。强调安全运营与组织整体战略目标的关联。 二、安全运营原则 确立安全运营的基本原则,如保密性、完整性和可用性。明确安全责任划分,确保各部门和人员履行安全职责。 三、安全风险评估与管理 进行全面的安…...
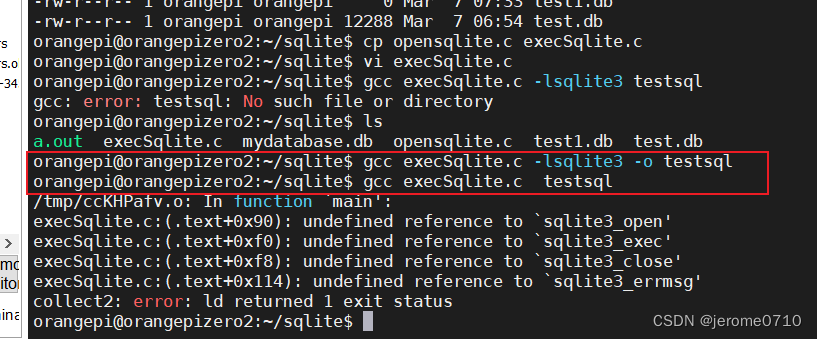
用C语言执行SQLite3的gcc编译细节
错误信息: /tmp/cc3joSwp.o: In function main: execSqlite.c:(.text0x100): undefined reference to sqlite3_open execSqlite.c:(.text0x16c): undefined reference to sqlite3_exec execSqlite.c:(.text0x174): undefined reference to sqlite3_close execSqlit…...
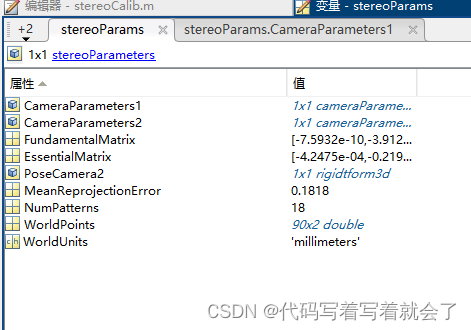
matlab双目相机标定-需要什么参数、怎么获得
相机标定目的:获得相机内参、外参、畸变系数,摄像头的内参(f,1/dx,1/dy,cx,cy)、畸变参数(k1,k2,k3,p1,p1)和外参(R,t),用于接下来的双目校正和深度图生成从而实现二维到三维的转换。 相机标定方法:opencv 双目相机标定以及立体…...
)
大型语言模型的智能助手:检索增强生成(RAG)
背景 在人工智能的浪潮中,大型语言模型(LLMs)如GPT系列和LLama系列在自然语言处理(NLP)领域取得了显著成就。它们能够完成复杂的语言任务,如文本摘要、机器翻译、甚至创作诗歌。然而,这些模型在…...
Ubuntu 安装谷歌拼音输入法
一、Fcitx 安装 在Ubuntu 下,谷歌拼音输入法是基于Fcitx输入法的。所以,首先需要安装Fcitx。一般来说,Ubuntu最新版中都默认安装了Fcitx,但是为了确保一下,我们可以在系统终端中运行如下命令: sudo apt ins…...
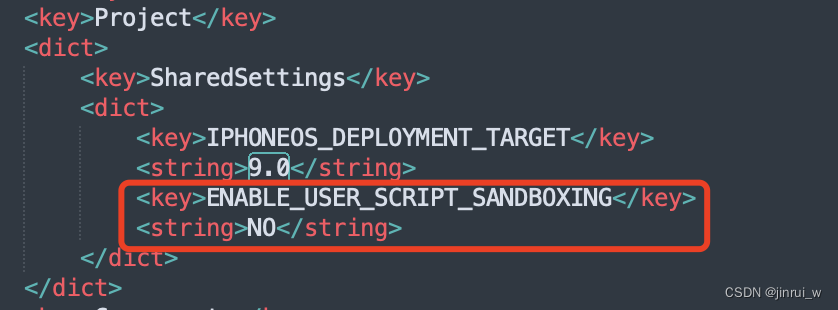
修改MonkeyDev默认配置适配Xcode15
上一篇文章介绍了升级Xcode15后,适配MonkeyDev的一些操作,具体操作可以查看:Xcode 15 适配 MonkeyDev。 但是每次新建项目都要去修改那些配置,浪费时间和精力,这篇文章主要介绍如何修改MonkeyDev的默认配置࿰…...

deepinlinux打包deb文件完善
最近学习了一篇qt入门文章,做了一个小应用,要给另一台电脑用时发现还需考虑另一台没有qt,要把相关库带过去,后来就学了打包成deb安装包,看起来更专业。 win下搜索qt依赖库的程序是windeployqt,先将应用输出…...

Android studioSDK集成:com.yechaoa.yutilskt
文章目录 1、工具介绍2、集成 1、工具介绍 com.yechaoa.yutilskt是一个Android开发工具库,提供了一些常用的工具类和方法,方便开发者进行Android应用程序的开发。该库包含了以下功能: 网络请求工具类:提供了简化的网络请求方法&…...

openssl3.2 - exp - PEM <==> DER
文章目录 openssl3.2 - exp - PEM <> DER概述笔记加密用的私钥(带口令保护) - PEM > DER加密用的私钥(不带口令保护) - DER > PEM将不带口令的PEM转成带口令的PEM支持口令的算法备注END openssl3.2 - exp - PEM <> DER 概述 想将客户端私钥 服务端公钥 数…...

云计算的部署方式(公有云、私有云、混合云、社区云)
云计算的部署方式(公有云、私有云、混合云、社区云) 目录 零、00时光宝盒 一、云计算的部署方式 1.1、公有云(Public Cloud) 1.2、私有云(Private Cloud) 1.3、混合云(Hybrid Cloud) 1.4、社区云&am…...
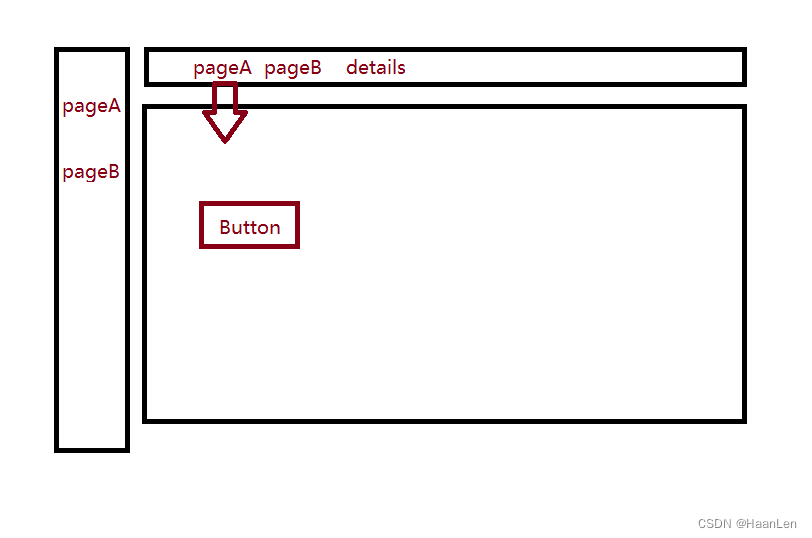
umi4 项目使用 keepalive 缓存页面(umi-plugin-keep-alive、react-activation)
umi4使用keepalive 配置文件config\config.ts export default defineConfig({plugins: [umi-plugin-keep-alive], });安装add umi-plugin-keep-alive yarn add umi-plugin-keep-alive页面 A import { KeepAlive, history, useAliveController } from umijs/max; const Page…...
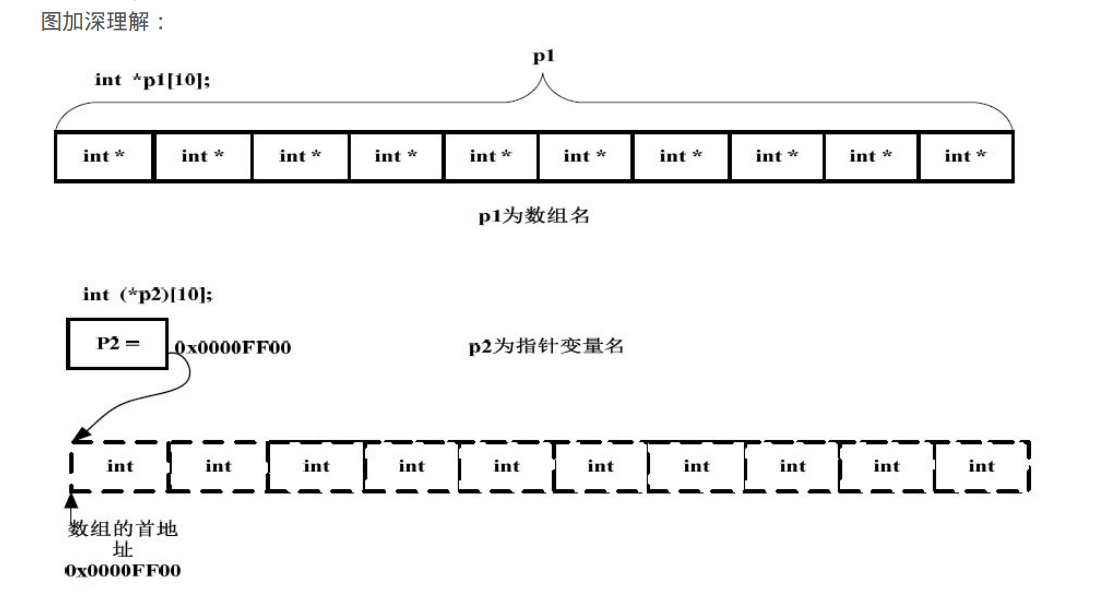
new;getline();重载<<和>>
面向对象程序设计的优点: 易维护易扩展模块化:通过设置访问级别,限制别人对自己的访问,保护了数据安全 int main(){ return 0;} 返回值0在windows下编程一般没用,但是在linux中编程,返回值有时有用 汇编与…...

python报错
Missing optional dependency ‘xlrd’. Install xlrd > 1.0.0 for Excel support Use pip or conda to install xlrd 安装xlrd库...
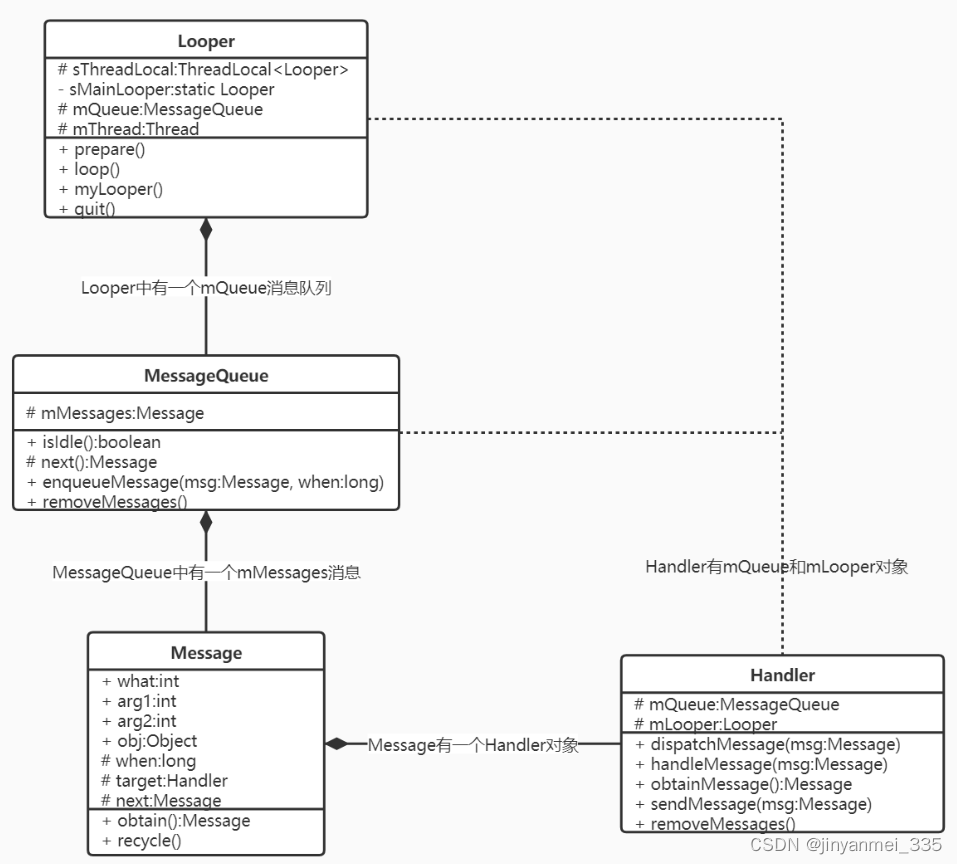
Android14 Handle机制
Handle是进程内部, 线程之间的通信机制. handle主要接受子线程发送的数据, 并用此数据配合主线程更新UI handle可以分发Message对象和Runnable对象到主线程中, 每个handle实例, 都会绑定到创建他的线程中, 它有两个作用,: (1) 安排消息在某个主线程中某个地方执行 (2) 安排…...

spark 总结
1.spark 配置文件 spark-default.conf spark.yarn.historyServer.address xiemeng-01:18080 spark.history.port18080 hive-site.xml <configuration><property><name>javax.jdo.option.ConnectionURL</name> </property><property>&…...
Gitlab修改仓库权限为public、Internal、Private
Public(公开):所有人都可以访问该仓库; Internal(内部):同一个GitLab群组或实例内的所有用户都可以访问该仓库; Private(私人):仅包括指定成员的用…...
)
Python语言例题集(008)
#!/usr/bin/python3 #建立链表类和遍历此链表 class Node(): def init(self,dataNone): self.datadata self.nextNone class LinkedList(): def init(self): self.headNone def printList(self):ptrself.headwhile ptr:print(ptr.data)ptrptr.nextlinkLinkedList() link.he…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...

淘宝扭蛋机小程序系统开发:打造互动性强的购物平台
淘宝扭蛋机小程序系统的开发,旨在打造一个互动性强的购物平台,让用户在购物的同时,能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机,实现旋转、抽拉等动作,增…...

tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号,此时,我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...

在RK3588上搭建ROS1环境:创建节点与数据可视化实战指南
在RK3588上搭建ROS1环境:创建节点与数据可视化实战指南 背景介绍完整操作步骤1. 创建Docker容器环境2. 验证GUI显示功能3. 安装ROS Noetic4. 配置环境变量5. 创建ROS节点(小球运动模拟)6. 配置RVIZ默认视图7. 创建启动脚本8. 运行可视化系统效果展示与交互技术解析ROS节点通…...

6.计算机网络核心知识点精要手册
计算机网络核心知识点精要手册 1.协议基础篇 网络协议三要素 语法:数据与控制信息的结构或格式,如同语言中的语法规则语义:控制信息的具体含义和响应方式,规定通信双方"说什么"同步:事件执行的顺序与时序…...