【自然语言处理】BitNet b1.58:1bit LLM时代
论文地址:https://arxiv.org/pdf/2402.17764.pdf
相关博客
【自然语言处理】【大模型】BitNet:用1-bit Transformer训练LLM
【自然语言处理】BitNet b1.58:1bit LLM时代
【自然语言处理】【长文本处理】RMT:能处理长度超过一百万token的Transformer
【自然语言处理】【大模型】MPT模型结构源码解析(单机版)
【自然语言处理】【大模型】ChatGLM-6B模型结构代码解析(单机版)
【自然语言处理】【大模型】BLOOM模型结构源码解析(单机版)
一、BitNet
BitNet采用了与Transformer基本一致的模型架构,仅将标准矩阵乘法层换成了BitLinear,其他组件仍然是高精度的。BitLinear主要是包含的操纵:权重量化、激活量化以及LayerNorm。
权重量化。通过减均值实现0中心化,然后用sign实现二值化。假设全精度权重为 W ∈ R n × m W\in\mathcal{R}^{n\times m} W∈Rn×m,则二值量化过程为
W ~ = Sign ( W − α ) (1) \widetilde{W}=\text{Sign}(W-\alpha) \tag{1} \\ W =Sign(W−α)(1)
Sign ( W i j ) = { + 1 , if W i j > 0 − 1 , if W i j ≤ 0 (2) \text{Sign}(W_{ij})=\begin{cases} +1,&&\text{if}\;W_{ij}>0 \\ -1,&&\text{if}\;W_{ij}\leq 0 \\ \end{cases} \tag{2} \\ Sign(Wij)={+1,−1,ifWij>0ifWij≤0(2)
α = 1 n m ∑ i j W i j (3) \alpha=\frac{1}{nm}\sum_{ij}W_{ij} \tag{3} \\ α=nm1ij∑Wij(3)
激活量化。使用absmax的方式将激活量化至b-bit。具体的实现方式是乘以 Q b Q_b Qb再除以输入矩阵的最大绝对值,从而将激活缩放至 [ − Q b , Q b ] ( Q b = 2 b − 1 ) [-Q_b,Q_b](Q_b=2^{b-1}) [−Qb,Qb](Qb=2b−1),即
x ~ = Quant ( x ) = Clip ( x × Q b γ , − Q b + ϵ , Q b − ϵ ) (4) \tilde{x}=\text{Quant}(x)=\text{Clip}(x\times\frac{Q_b}{\gamma},-Q_b+\epsilon,Q_b-\epsilon) \tag{4}\\ x~=Quant(x)=Clip(x×γQb,−Qb+ϵ,Qb−ϵ)(4)
Clip ( x , a , b ) = max ( a , min ( b , x ) ) , γ = ∥ x ∥ ∞ (5) \text{Clip}(x,a,b)=\max(a,\min(b,x)),\quad\gamma=\parallel x\parallel_\infty \tag{5} \\ Clip(x,a,b)=max(a,min(b,x)),γ=∥x∥∞(5)
其中 ϵ \epsilon ϵ是防止裁剪时溢出的小浮点数。
对于非线性函数之前的激活值则采用不同的量化方式,通过减轻最小值的方式将其缩放至 [ 0 , Q b ] [0,Q_b] [0,Qb],从而保证所有值均为非负:
x ~ = Quant ( x ) = Clip ( ( x − η ) × Q b γ , ϵ , Q b − ϵ ) , η = min i , j x i j (6) \tilde{x}=\text{Quant}(x)=\text{Clip}((x-\eta)\times\frac{Q_b}{\gamma},\epsilon,Q_b-\epsilon),\quad\eta=\min_{i,j}x_{ij}\tag{6} \\ x~=Quant(x)=Clip((x−η)×γQb,ϵ,Qb−ϵ),η=i,jminxij(6)
LayerNorm。在对激活值量化前,为了保证量化后的方差稳定,采用了SubLN。
BitLinear的完成计算过程为
y = W ~ x ~ = W ~ Quant ( LN ( x ) ) × β γ Q b (7) y=\widetilde{W}\tilde{x}=\widetilde{W}\text{Quant}(\text{LN}(x))\times\frac{\beta\gamma}{Q_b}\tag{7} \\ y=W x~=W Quant(LN(x))×Qbβγ(7)
LN ( x ) = x − E ( x ) Var ( x ) + ϵ , β = 1 n m ∥ W ∥ 1 (8) \text{LN}(x)=\frac{x-E(x)}{\sqrt{\text{Var}(x)+\epsilon}},\quad\beta=\frac{1}{nm}\parallel W\parallel_1 \tag{8} \\ LN(x)=Var(x)+ϵx−E(x),β=nm1∥W∥1(8)
二、BitNet b1.58
BitNet b1.58在BitNet的基础上做了一些修改。
权重量化。采用absmean的方式将权重约束在 { − 1 , 0 , 1 } \{-1,0,1\} {−1,0,1}中,而BitNet则将权重约束为二值 { − 1 , 1 } \{-1,1\} {−1,1}。具体来说,先使用平均绝对值来缩放权重,然后通过舍入的方式转换为 { − 1 , 0 , 1 } \{-1,0,1\} {−1,0,1}:
W ~ = RoundClip ( W γ + ϵ , − 1 , 1 ) (9) \widetilde{W}=\text{RoundClip}(\frac{W}{\gamma+\epsilon},-1,1)\tag{9} \\ W =RoundClip(γ+ϵW,−1,1)(9)
RoundClip ( x , a , b ) = max ( a , min ( b , round ( x ) ) ) (10) \text{RoundClip}(x,a,b)=\max(a,\min(b,\text{round}(x)))\tag{10} \\ RoundClip(x,a,b)=max(a,min(b,round(x)))(10)
γ = 1 n m ∑ i j ∣ W i j ∣ (11) \gamma=\frac{1}{nm}\sum_{ij}|W_{ij}|\tag{11} \\ γ=nm1ij∑∣Wij∣(11)
激活量化。同BitNet一样,但是对于非线性函数前的激活不再量化至 [ 0 , Q b ] [0,Q_b] [0,Qb],而是都量化至 [ − Q b , Q b ] [-Q_b,Q_b] [−Qb,Qb]。
此外,为了能够方便于开源软件兼容,整体结构采用类似LLaMA的结构。具体来说,使用RMSNorm、SwiGLU、RoPE并移除所有偏置。
三、实验
1. 困惑度
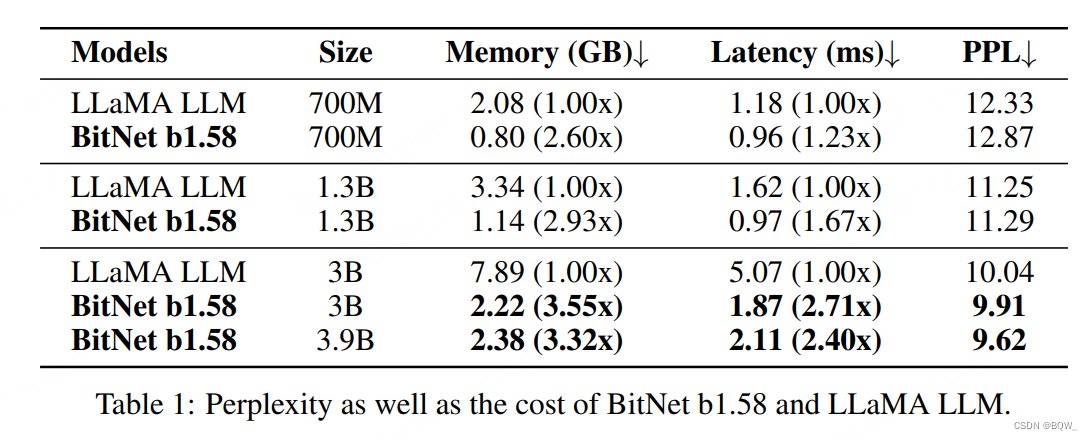
BitNet b1.58在3B大小时,困惑度与LLaMA相匹配,但是速度快2.71倍且显存使用减少3.55倍。当BitNet b1.58大小为3.9B时,速度快2.4倍且显存减少3.32倍,并且效果显著优于LLaMA 3B。
2. 下游任务
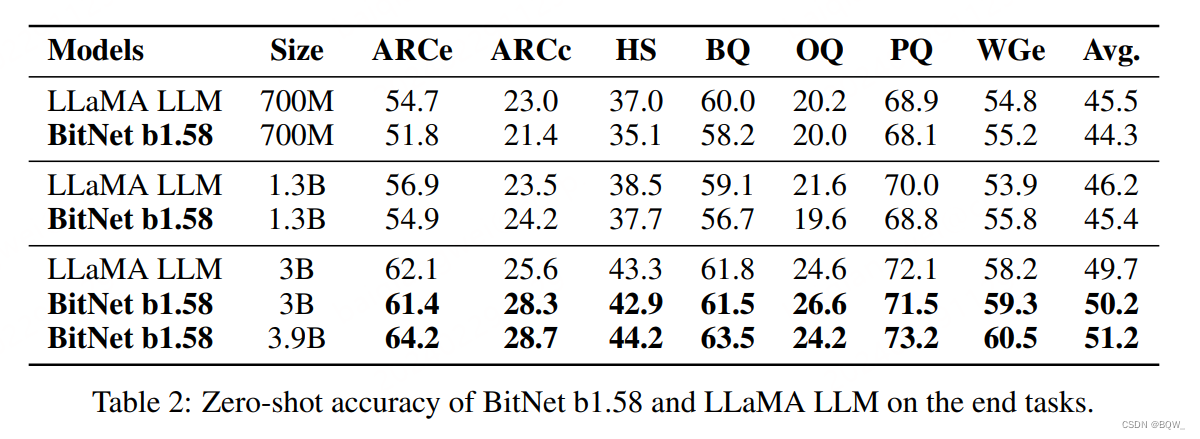
随着模型尺寸的增加,BitNet b1.58和LLaMA在下游任务上的差距逐步缩小。在尺寸达到3B时,BitNet b.158能够与全精度相匹配。
3. 显存和延时
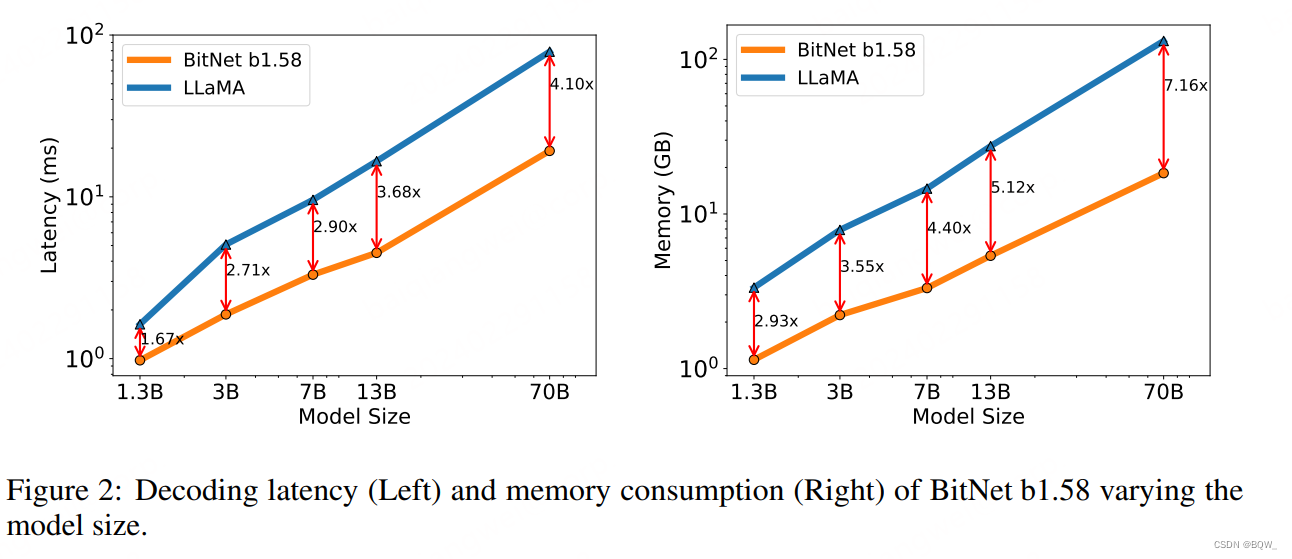
随着模型尺寸的增加,BitNet b1.58的速度优势和显存优势会更加明显。
4. 能耗
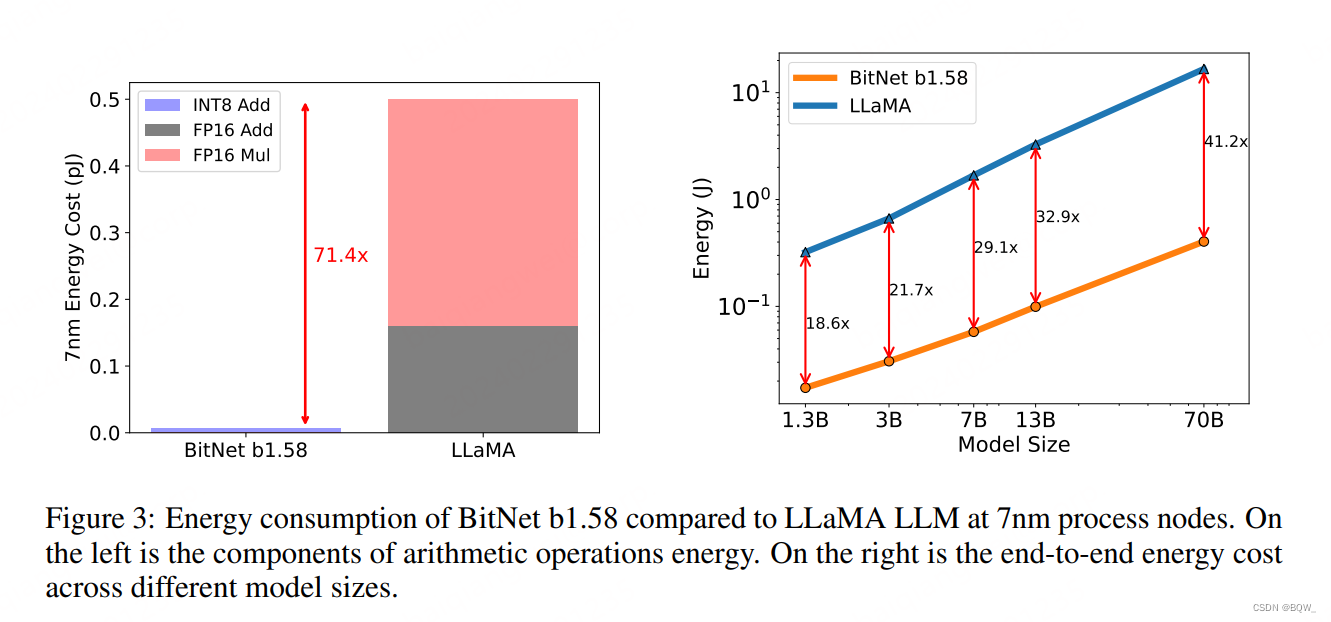
矩阵乘法是LLM中能耗最高的部分。BitNet b1.58主要是INT8的加法计算,而LLaMA则是由FP16加法和乘法组成。在7nm芯片上,BitNet b1.58能够节约71.4倍的计算能耗。随着模型尺寸的增加,BitNet b1.58在能耗方面会越来越高效。
5. 吞吐

相同机器下,BitNet b1.58的batch size是LLaMA LLM的11倍,吞吐则是8.9倍。
相关文章:

【自然语言处理】BitNet b1.58:1bit LLM时代
论文地址:https://arxiv.org/pdf/2402.17764.pdf 相关博客 【自然语言处理】【大模型】BitNet:用1-bit Transformer训练LLM 【自然语言处理】BitNet b1.58:1bit LLM时代 【自然语言处理】【长文本处理】RMT:能处理长度超过一百万t…...
【Axure高保真原型】可视化动点素材
今天和粉丝们免费分享可视化动点素材的原型模板,该模板使用简单,复制粘贴,预览时即可实现动点效果,本案例提供红黄蓝绿4中颜色的动点,如果需要其他颜色,可以自行编辑svg里面的代码 【原型效果】 【模板下载…...

分布式数据库 GaiaDB-X 金融应用实践
1 银行新一代核心系统建设背景及架构 在银行的 IT 建设历程中,尤其是中大行,大多都基于大型机和小型机来构建核心系统。随着银行业务的快速发展,这样的系统对业务的支持越来越举步维艰,主要体现在以下四个方面: 首先是…...

机器学习中的经典算法总结
经典算法 有监督算法逻辑回归支持向量机SVM决策树朴素贝叶斯K近邻(KNN) 无监督算法K-meansPCA主成分分析预留模版 有监督算法 逻辑回归 简介 逻辑回归是机器学习中一种经典的分类算法,通常用于二分类任务,基本思想是构建一个线性…...
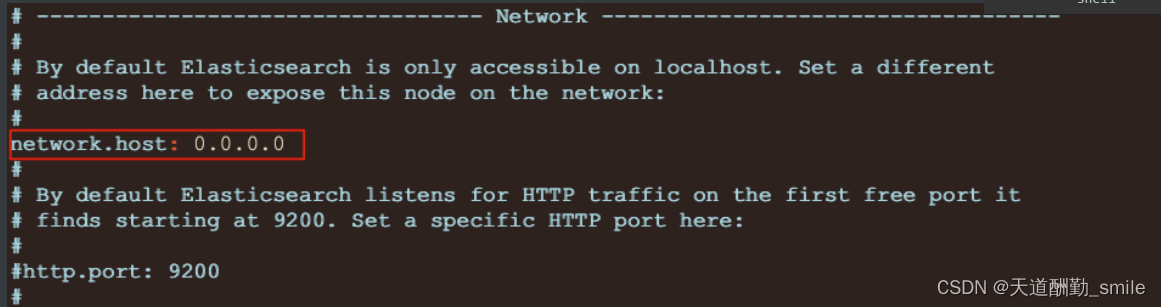
ElasticSearch 学习(docker,传统方式安装、安装遇到的问题解决,)
目录 简介 什么是ElasticSearch 安装 传统方式安装 开启远程访问 Docker方式安装 Kibana 简介 安装 传统方式安装 Docker方式安装 compose方式安装 简介 什么是ElasticSearch ElasticSearch 简称 ES ,是基于Apache Lucene构建的开源搜索引擎,…...
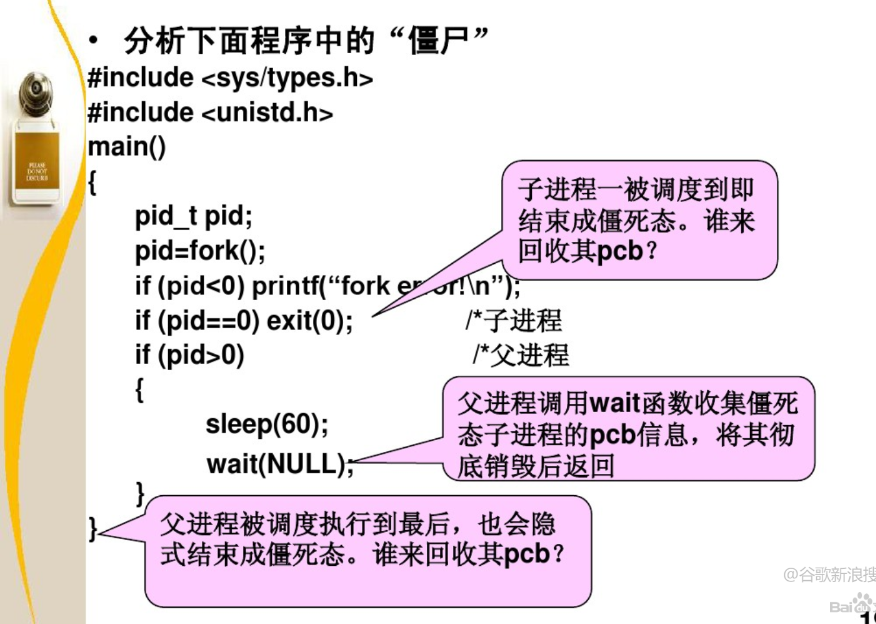
[百度二面]操作系统进程、锁相关面试题
2.22 什么是死锁 在多道程序环境下,多个进程可以竞争有限数量的资源。当一个进程申请资源时,如果这时没有可用资源,那么这个进程进入等待状态。有时,如果所申请的资源被其他等待进程占有,那么该等待进程有可能再也无法…...

IP劫持的危害及应对策略
随着互联网的发展,网络安全问题日益凸显,其中IP劫持作为一种常见的网络攻击手段,对个人和企业的信息安全造成了严重的威胁。IP数据云将分析IP劫持的危害,并提出相应的应对策略。 IP地址查询:IP数据云 - 免费IP地址查询…...

Mac安装oh-my-zsh
目录 命令下载 卸载命令 注意 命令下载 curl -L https://raw.github.com/robbyrussell/oh-my-zsh/master/tools/install.sh | sh 卸载命令 uninstall_oh_my_zsh 注意 终端init的时候并不会执行~/.bash_profile、~/.bashrc等脚本了, 这是因为其默认启动执行脚本…...

【Web开发】深度学习HTML(超详细,一篇就够了)
💓 博客主页:从零开始的-CodeNinja之路 ⏩ 收录文章:【Web开发】深度学习html(超详细,一篇就够了) 🎉欢迎大家点赞👍评论📝收藏⭐文章 目录 HTML1. HTML基础1.1 什么是HTML1.2 认识HTML标签1.3 HTML文件基本…...
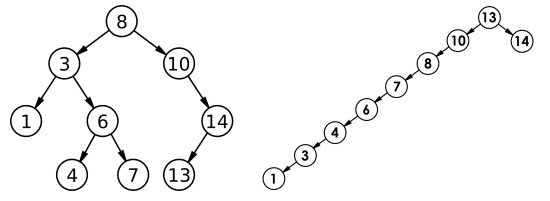
深入了解二叉搜索树:原理、实现与应用
目录 一、介绍二叉搜索树 二、二叉搜索树的基本性质 三、二叉搜索树的实现 四、总结 在计算机科学中,数据结构是构建算法和程序的基础。其中,二叉搜索树(Binary Search Tree,简称 BST)作为一种常见的数据结构&#…...
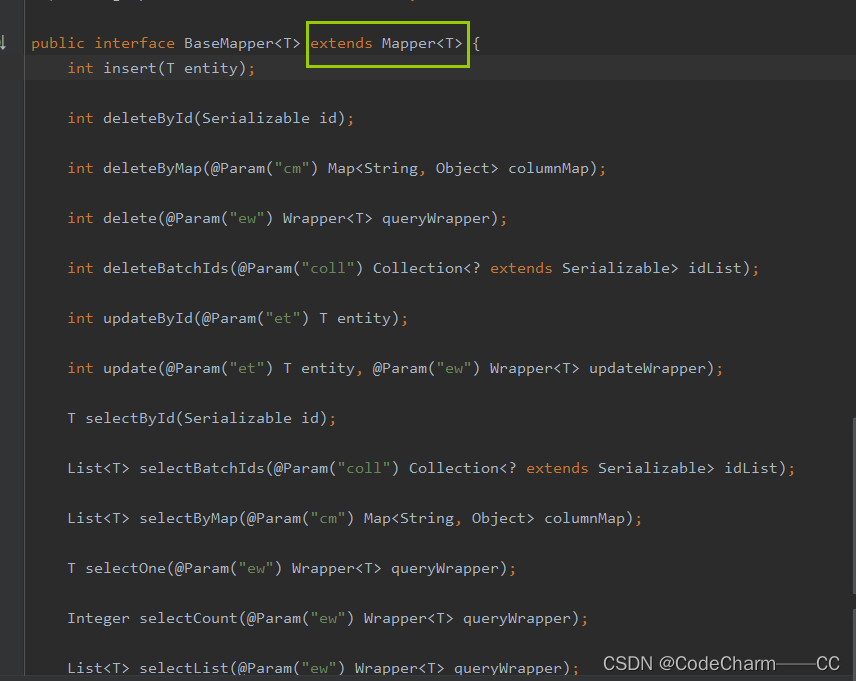
【MybatisPlus】BaseMapper详解,举例说明
一、BaseMapper 简介 MyBatis-Plus 的核心类 BaseMapper 主要是用于提供基本的 CRUD(创建、读取、更新、删除)操作的接口定义。它是 MyBatis-Plus 框架中的一个重要组成部分,可以大大简化基于 MyBatis 的数据访问层代码的编写。 BaseMapper…...

LightDB24.1 oracle_fdw支持服务端GBK编码
功能介绍 oracle_fdw是一个PG的插件,用于连接oracle数据库,由于原生PG不支持服务端GBK编码,所以原生的oracle_fdw也不支持服务端GBK编码。在LightDB23.3中支持了服务端GBK编码,导致在GBK编码的数据库中使用oracle_fdw时报错。 Li…...
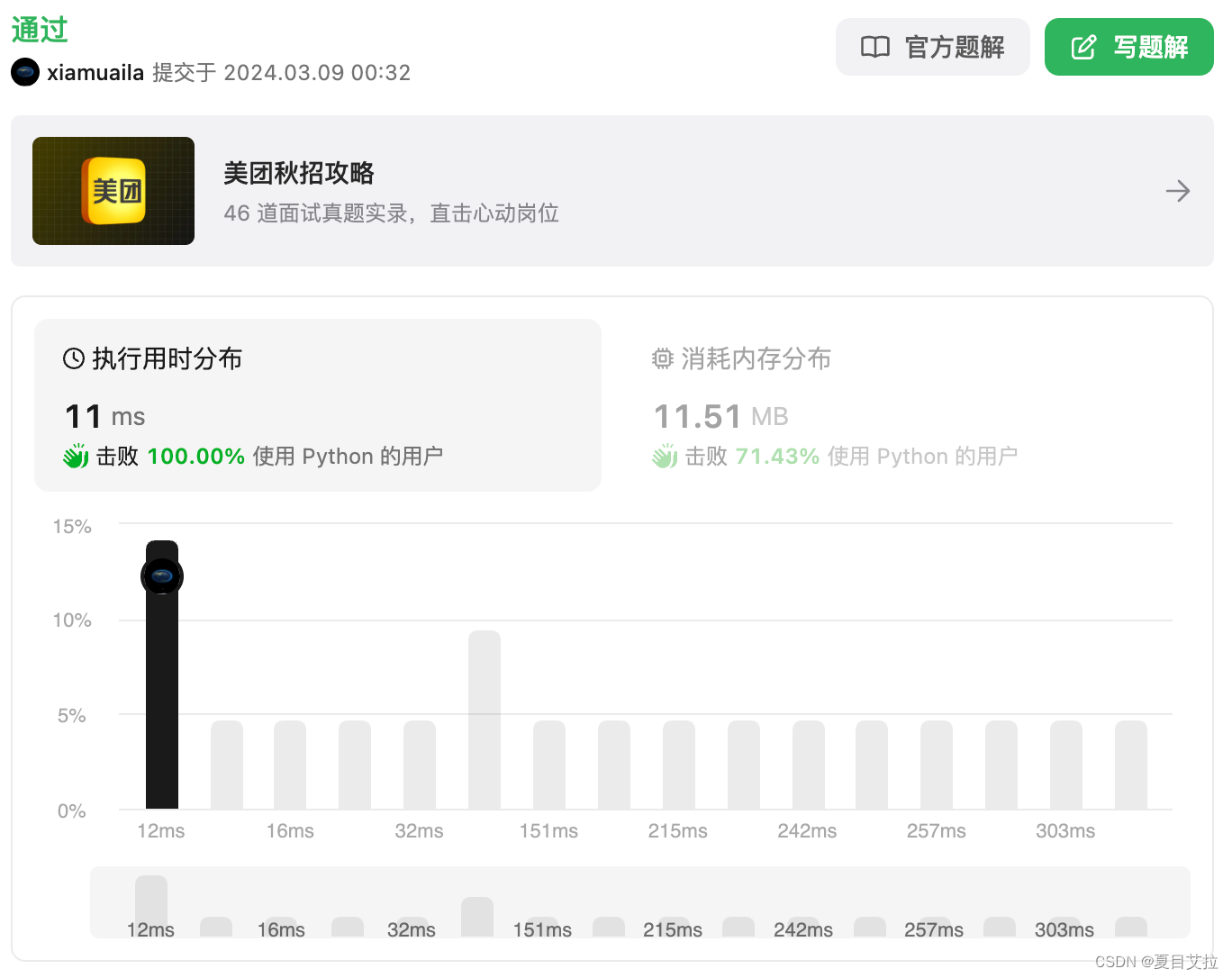
算法 环形数组是否存在循环 力扣执行速度击败100%
目录 题目 leetcode 457 求解思路 代码 结果 题目 leetcode 457 存在一个不含 0 的 环形 数组 nums ,每个 nums[i] 都表示位于下标 i 的角色应该向前或向后移动的下标个数: 如果 nums[i] 是正数,向前(下标递增方向࿰…...

FFmpeg——开源的开源的跨平台音视频处理框架简介
引言: FFmpeg是一个开源的跨平台音视频处理框架,可以处理多种音视频格式。它由Fabrice Bellard于2000年创建,最初是一个只包括解码器的项目。后来,很多开发者参与其中,为FFmpeg增加了多种新的功能,例如编码…...

怎么看待Groq
用眼睛看。 就是字面上的意思用眼睛看。 我属于第一波玩到的,先给大家一个直观的印象,Groq到底有多快。 目前Groq只能选Llama的70b,和Mixtral的MoE,那我选7*8的这个MoE模型来实验。 这么好些字大概花了不到1秒,流式响应,其实是不是流式已经没那么重要了 ,然后看每秒Toke…...
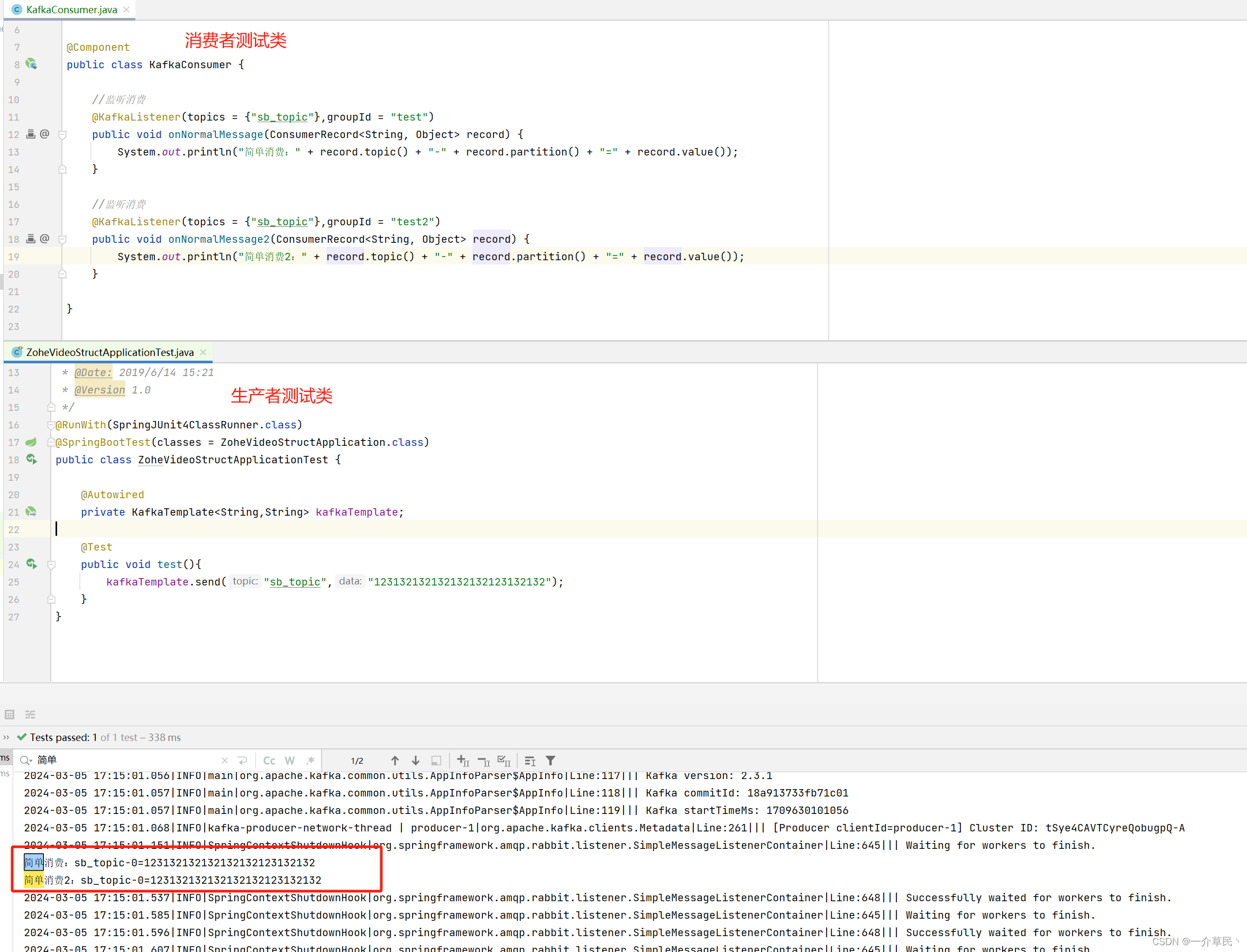
Kafka | SpringBoot集成Kafka
SpringBoot集成Kafka 一、前言二、项目1. pom2. application.properties4. 消息生产者-测试5. 消息消费者 三、启动测试四、有总结的不对的地方/或者问题 请指正, 我在努力中 一、前言 该文章中主要对SpringBoot 集成Kafka 主要是 application.properties 与 pom坐标就算集成完…...

python的tqdm库不显示动态进度条的问题
python的tqdm库不显示动态进度条的问题 本质原因是tqdm无法获取内部对象的长度,这可能是因为内部对象是一个迭代器,问题经常发生在同时使用tqdm与enumerate的场合,例如深度学习中经常可能出现的: tqdm.tqdm(enumerate(train_loade…...
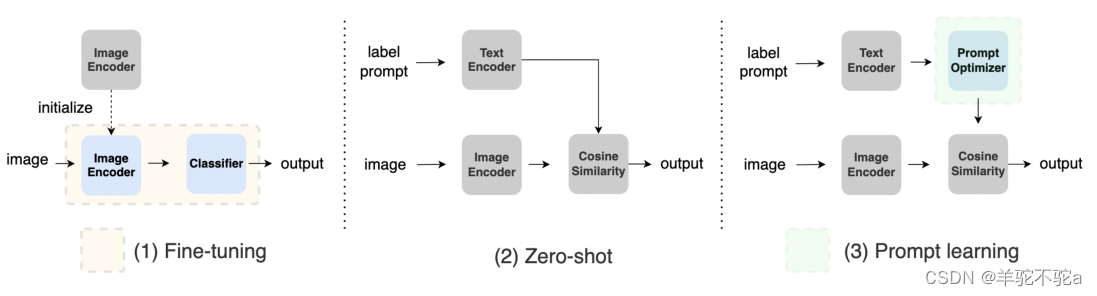
【prompt四】Domain Prompt Learning for Efficiently Adapting CLIP to Unseen Domains
motivation 领域泛化(DG)是一个复杂的迁移学习问题,旨在学习未知领域的可泛化模型。最近的基础模型(FMs)对许多分布变化都具有鲁棒性,因此,应该从本质上提高DG的性能。在这项工作中,我们研究了采用视觉语言基础模型CLIP来解决图像分类中的DG问题的通用方法。虽然ERM使用标…...

利用Amazon Bedrock畅玩Claude 3等多种领先模型,抢占AI高地(体验倒计时4小时)
快乐的时间总是短暂的,Claude 3 在亚马逊云科技上限时体验仅剩4小时,上次分享了入门级操作教程,本期给大家带来AWS Lambda Amazon Bedrock一起构建可以便捷使用的Claude 3接口 AWS Lambda AWS Lambda 是一项计算服务,可以运行您…...

MySql分布式事务
1 seata 底层原理 Seata(Simple Extensible Autonomous Transaction Architecture)是一个开源的分布式事务解决方案,其底层原理主要基于改进的传统2PC(Two-Phase Commit,两阶段提交)协议,并结合…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...
