算法 环形数组是否存在循环 力扣执行速度击败100%
目录
题目 leetcode 457
求解思路
代码
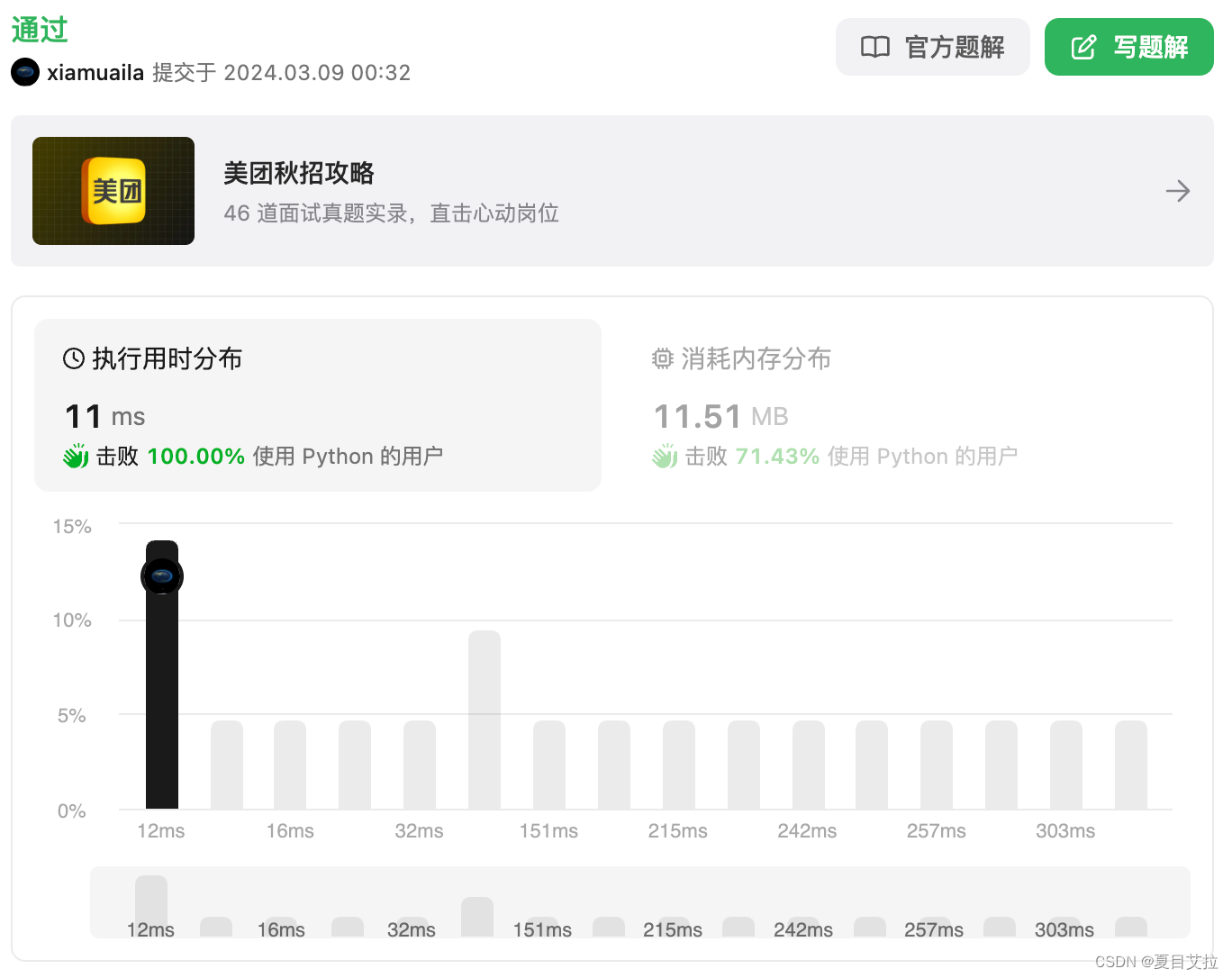
结果
题目 leetcode 457
存在一个不含 0 的 环形 数组 nums ,每个 nums[i] 都表示位于下标 i 的角色应该向前或向后移动的下标个数:
- 如果
nums[i]是正数,向前(下标递增方向)移动|nums[i]|步 - 如果
nums[i]是负数,向后(下标递减方向)移动|nums[i]|步
因为数组是 环形 的,所以可以假设从最后一个元素向前移动一步会到达第一个元素,而第一个元素向后移动一步会到达最后一个元素。
数组中的 循环 由长度为 k 的下标序列 seq 标识:
- 遵循上述移动规则将导致一组重复下标序列
seq[0] -> seq[1] -> ... -> seq[k - 1] -> seq[0] -> ... - 所有
nums[seq[j]]应当不是 全正 就是 全负 k > 1
如果 nums 中存在循环,返回 true ;否则,返回 false 。
示例 1:
输入:nums = [2,-1,1,2,2] 输出:true 解释:存在循环,按下标 0 -> 2 -> 3 -> 0 。循环长度为 3 。
示例 2:
输入:nums = [-1,2] 输出:false 解释:按下标 1 -> 1 -> 1 ... 的运动无法构成循环,因为循环的长度为 1 。根据定义,循环的长度必须大于 1 。
示例 3:
输入:nums = [-2,1,-1,-2,-2] 输出:false 解释:按下标 1 -> 2 -> 1 -> ... 的运动无法构成循环,因为 nums[1] 是正数,而 nums[2] 是负数。 所有 nums[seq[j]] 应当不是全正就是全负。
提示:
1 <= nums.length <= 5000-1000 <= nums[i] <= 1000nums[i] != 0
求解思路
首先定义一个工具函数next_index求下一个索引,值得注意的是python支持这种方法内部定义方法的方式
然后对每个下标起点进行遍历
如果nums[i] 为 0,则代表这里会卡死,要跳过
我们让fast指针快slow一步,一个是方便后面的代码,二个是加快执行效率,让快指针更快追上慢指针,得出是否存在循环
while作检测,检查慢指针和当前快指针指向的数字,也就是移动步数是否同号(题目要求循环的路径要同号),检查慢指针和快指针下一步位置是否同号
如果同号,继续比较快慢指针现在是否相等,如果相当,还要检查慢指针下一步位置是不是自己(题目要求路径长度至少为2),如果不是自己才能return True
如果不相当,则让快指针两步走,慢指针一步走
直到while循环结束,还没return结果,执行下面的代码
接下来的代码是性能提升关键,不加上的话只能击败9.52%的人,,
我需要重新让慢指针为i,一切重新开始,让慢指针一步步走,一步步把它走过的地方变成0,让以后再来到这里就知道这里没有结果
代码
class Solution(object):def circularArrayLoop(self, nums):def next_index(i):return (i + nums[i]) % len(nums)for i in range(len(nums)):if nums[i] == 0:continueslow, fast = i, next_index(i)while nums[slow] * nums[fast] > 0 and nums[slow] * nums[next_index(fast)] > 0:if slow == fast:if slow == next_index(slow):breakreturn Trueslow = next_index(slow)fast = next_index(next_index(fast))# 性能提升slow = i while nums[slow] * nums[next_index(slow)] > 0:tmp = slow slow = next_index(slow)nums[tmp] = 0return False结果
相关文章:

算法 环形数组是否存在循环 力扣执行速度击败100%
目录 题目 leetcode 457 求解思路 代码 结果 题目 leetcode 457 存在一个不含 0 的 环形 数组 nums ,每个 nums[i] 都表示位于下标 i 的角色应该向前或向后移动的下标个数: 如果 nums[i] 是正数,向前(下标递增方向࿰…...

FFmpeg——开源的开源的跨平台音视频处理框架简介
引言: FFmpeg是一个开源的跨平台音视频处理框架,可以处理多种音视频格式。它由Fabrice Bellard于2000年创建,最初是一个只包括解码器的项目。后来,很多开发者参与其中,为FFmpeg增加了多种新的功能,例如编码…...

怎么看待Groq
用眼睛看。 就是字面上的意思用眼睛看。 我属于第一波玩到的,先给大家一个直观的印象,Groq到底有多快。 目前Groq只能选Llama的70b,和Mixtral的MoE,那我选7*8的这个MoE模型来实验。 这么好些字大概花了不到1秒,流式响应,其实是不是流式已经没那么重要了 ,然后看每秒Toke…...
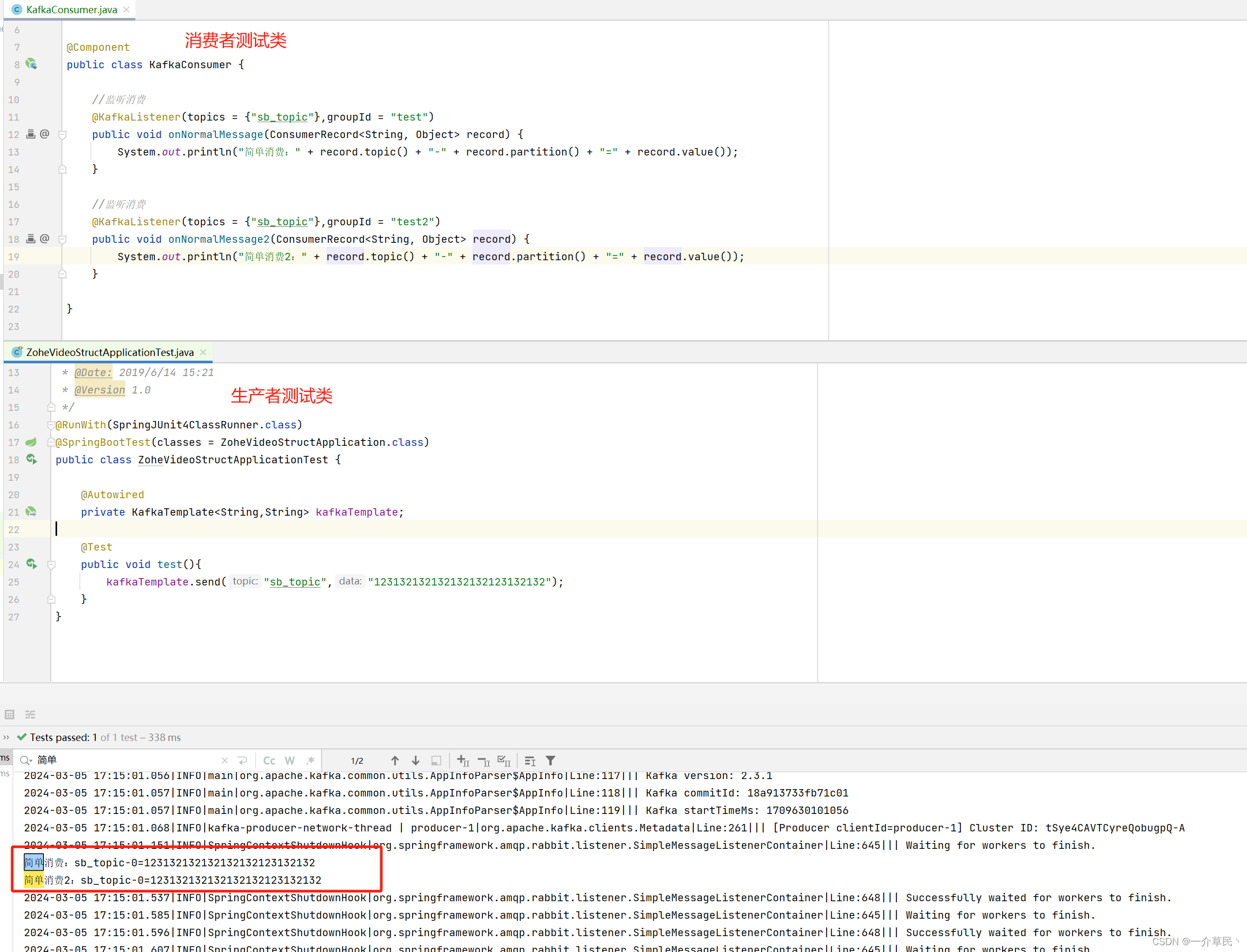
Kafka | SpringBoot集成Kafka
SpringBoot集成Kafka 一、前言二、项目1. pom2. application.properties4. 消息生产者-测试5. 消息消费者 三、启动测试四、有总结的不对的地方/或者问题 请指正, 我在努力中 一、前言 该文章中主要对SpringBoot 集成Kafka 主要是 application.properties 与 pom坐标就算集成完…...

python的tqdm库不显示动态进度条的问题
python的tqdm库不显示动态进度条的问题 本质原因是tqdm无法获取内部对象的长度,这可能是因为内部对象是一个迭代器,问题经常发生在同时使用tqdm与enumerate的场合,例如深度学习中经常可能出现的: tqdm.tqdm(enumerate(train_loade…...
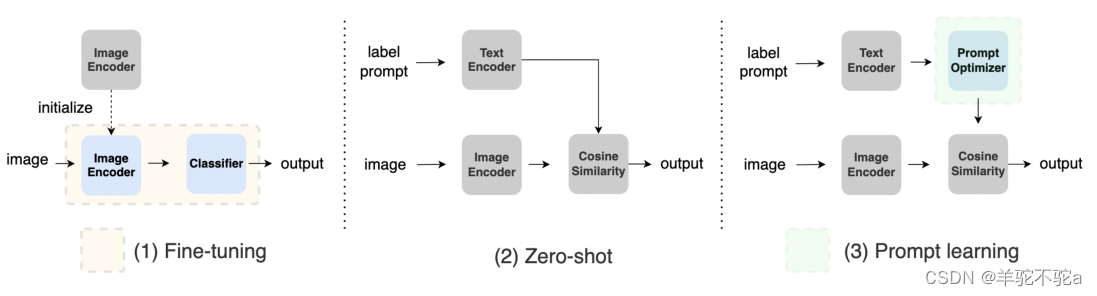
【prompt四】Domain Prompt Learning for Efficiently Adapting CLIP to Unseen Domains
motivation 领域泛化(DG)是一个复杂的迁移学习问题,旨在学习未知领域的可泛化模型。最近的基础模型(FMs)对许多分布变化都具有鲁棒性,因此,应该从本质上提高DG的性能。在这项工作中,我们研究了采用视觉语言基础模型CLIP来解决图像分类中的DG问题的通用方法。虽然ERM使用标…...

利用Amazon Bedrock畅玩Claude 3等多种领先模型,抢占AI高地(体验倒计时4小时)
快乐的时间总是短暂的,Claude 3 在亚马逊云科技上限时体验仅剩4小时,上次分享了入门级操作教程,本期给大家带来AWS Lambda Amazon Bedrock一起构建可以便捷使用的Claude 3接口 AWS Lambda AWS Lambda 是一项计算服务,可以运行您…...

MySql分布式事务
1 seata 底层原理 Seata(Simple Extensible Autonomous Transaction Architecture)是一个开源的分布式事务解决方案,其底层原理主要基于改进的传统2PC(Two-Phase Commit,两阶段提交)协议,并结合…...

android基础学习
从上面的描述就可以知道,每一个Activity组件都有一个对应的ViewRoot对象、View对象以及WindowManager.LayoutParams对象。这三个对象的对应关系是由WindowManagerImpl类来维护的。具体来说,就是由WindowManagerImpl类的成员变量mRoots、mViews和mParams所…...
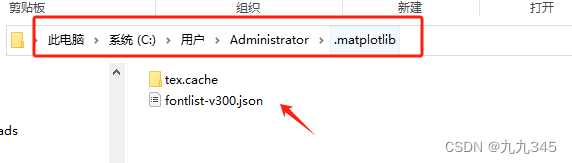
解决方案:Python画图汉字丢失显示小方块
解决方案: linux python解决中文字体 - jingsupo - 博客园 (cnblogs.com) 在找字体缓存文件的时候我找了一会儿,我的路径是这里: 做了所有更改之后,最后一定要把缓存文件删掉,不然还是会报同样的错误的。 这里再贴一…...

JWT的是什么
session共享 什么是session共享 Session共享是指在分布式系统中,在多个服务器之间共享同一个用户的会话数据。在传统的Web应用中,用户的会话信息通常存储在服务器端的Session中,而每个用户的请求在同一个服务器上处理,因此可以轻…...

git常用命令集合
1.差异对比 显示出branch1和branch2中差异的部分 git diff branch1 branch2 --stat显示出所有有差异的文件的详细差异 git diff branch1 branch2查看branch1分支有,而branch2中没有的log git log branch1 ^branch22.分支 列出所有本地分支 git branch列出所有远…...

UDP通信发送和接收 || UDP实现全双工通信
recvfrom ssize_t recvfrom(int sockfd, void *buf, size_t len, int flags, struct sockaddr *src_addr, socklen_t *addrlen); 功能: 从套接字中接收数据 参数: sockfd:套接字文件描述符 buf:存放数据空间首地址 …...
Mac 以SH脚本安装Arthas
SH脚本安装Aethas curl -L https://alibaba.github.io/arthas/install.sh | sh安装脚本说明 示例源文件: #! /bin/bash# temp file of as.sh TEMP_ARTHAS_FILE"./as.sh.$$"# target file of as.sh TARGET_ARTHAS_FILE"./as.sh"# update timeo…...
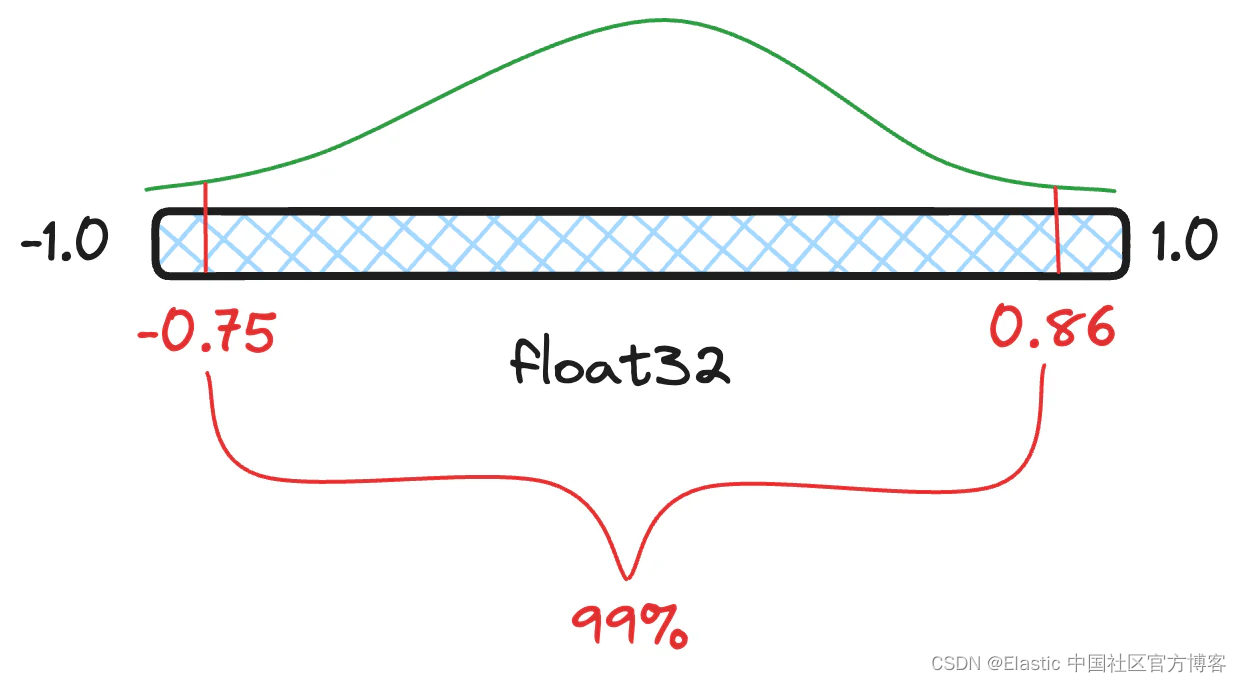
Elasticsearch:dense vector 数据类型及标量量化
密集向量(dense_vector)字段类型存储数值的密集向量。 密集向量场主要用于 k 最近邻 (kNN) 搜索。 dense_vector 类型不支持聚合或排序。 默认情况下,你可以基于 element_type 添加一个 dend_vector 字段作为 float 数值数组: …...
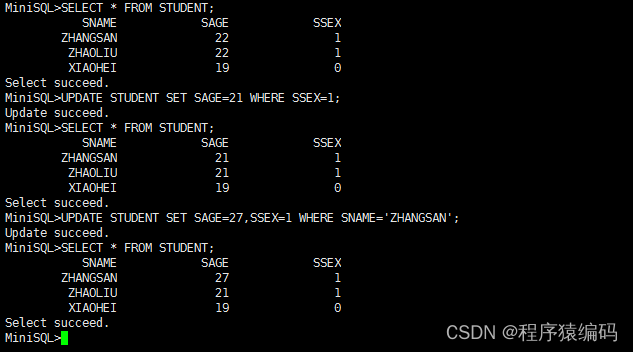
Linux C/C++下使用Lex/Yacc构建实现DBMS(Minisql)
DBMS(数据库管理系统)是一种用于管理和组织数据库的软件系统。它的重要性在于提供了一种有效地存储、管理和访问大量数据的方式。本文将深入探讨如何使用C语言、Lex(词法分析器生成器)和Yacc(语法分析器生成器…...
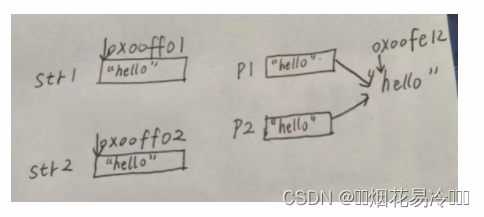
c语言指针小白基础教学
指针 1. 什么是指针?2. 如何编址(即如何给地址分配空间呢)3. 概念和基本术语3.1指针的值指针所指向的地址/内存区3.2 指针的类型(指针本身的类型)思考: 3.3 指针所指向的类型3.4 指针本身所占据的内存区3.5…...

面向对象设计之里氏替换原则
设计模式专栏:http://t.csdnimg.cn/4Mt4u 思考:什么样的代码才算违反里氏替换原则? 目录 1.里氏替换原则的定义 2.里氏替换原则与多态的区别 3.违反里氏替换原则的反模式 4.总结 1.里氏替换原则的定义 里氏替换原则(Liskov S…...
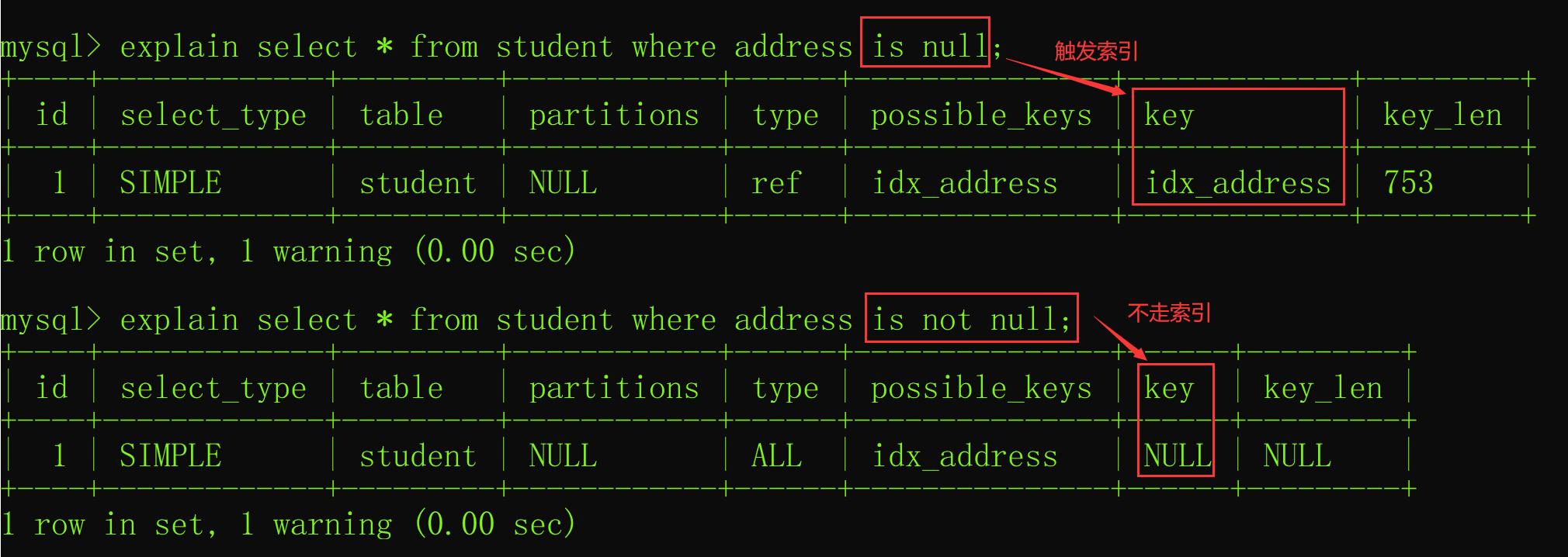
MySQL·SQL优化
目录 一 . 前言 二 . 优化方法 1 . 索引 (1)数据构造 (2)单索引 (3)explain (4)组合索引 (5)索引总结 2 . 避免使用select * 3 . 用union all代替u…...

Dockerfile指令大全
Dockerfile文件由一系列指令和参数组成。指令的一般格式为INSTRUCTION arguments。具体来说,包括"配置指令"(配置镜像信息)和"操作指令"(具体执行操作)。每条指令,如FROM,都是大小写不敏感的。但是为了区分指令和参数&am…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...
