Codeforces-1935E:Distance Learning Courses in MAC(思维)
E. Distance Learning Courses in MAC
time limit per test 2 seconds
memory limit per test 256 megabytes
input standard input
output standard output
The New Year has arrived in the Master’s Assistance Center, which means it’s time to introduce a new feature!
Now students are given distance learning courses, with a total of n n n courses available. For the i i i-th distance learning course, a student can receive a grade ranging from x i x_i xi to y i y_i yi.
However, not all courses may be available to each student. Specifically, the j j j-th student is only given courses with numbers from l j l_j lj to r j r_j rj, meaning the distance learning courses with numbers l j , l j + 1 , … , r j l_j,l_{j+1},…,r_j lj,lj+1,…,rj.
The creators of the distance learning courses have decided to determine the final grade in a special way. Let the j j j-th student receive grades c l j , c l j + 1 , … , c r j c_{l_j},c_{l_{j+1}},…,c_{r_j} clj,clj+1,…,crj for their distance learning courses. Then their final grade will be equal to c l j ∣ c l j + 1 ∣ … ∣ c r j c_{l_j} |\ c_{l_{j+1}} |\ …\ | c_{r_j} clj∣ clj+1∣ … ∣crj, where | denotes the bitwise OR operation.
Since the chatbot for solving distance learning courses is broken, the
students have asked for your help. For each of the q q q students, tell them the maximum final grade they can achieve.
Input
Each test consists of multiple test cases. The first line contains a single integer t ( 1 ≤ t ≤ 2 ⋅ 1 0 4 ) t (1\le t\le 2⋅10^4) t(1≤t≤2⋅104) — the number of test cases. The description of the test cases follows.
The first line of each test case contains a single integer n ( 1 ≤ n ≤ 2 ⋅ 1 0 5 ) n (1\le n\le 2⋅10^5) n(1≤n≤2⋅105) — the number of distance learning courses.
Each of the following n n n lines contains two integers x i x_i xi and y i y_i yi ( 0 ≤ x i ≤ y i < 2 30 ) (0\le x_i\le y_i\lt2^{30}) (0≤xi≤yi<230) — the minimum and maximum grade that can be received for the i i i-th course.
The next line contains a single integer q ( 1 ≤ q ≤ 2 ⋅ 1 0 5 ) q (1\le q\le2⋅10^5) q(1≤q≤2⋅105) — the number of students.
Each of the following q q q lines contains two integers l j l_j lj and r j r_j rj ( 1 ≤ l j ≤ r j ≤ n ) (1\le l_j\le r_j\le n) (1≤lj≤rj≤n) — the minimum and maximum course numbers accessible to the j j j-th student.
It is guaranteed that the sum of n n n over all test cases and the sum of q q q over all test cases do not exceed 2 ⋅ 1 0 5 2⋅10^5 2⋅105.
Output
For each test case, output q q q integers, where the j j j-th integer is the maximum final grade that the j j j-th student can achieve.
Example
input
3
2
0 1
3 4
3
1 1
1 2
2 2
4
1 7
1 7
3 10
2 2
5
1 3
3 4
2 3
1 4
1 2
6
1 2
2 2
0 1
1 1
3 3
0 0
4
3 4
5 5
2 5
1 2
output
1 5 4
15 11 15 15 7
1 3 3 3
思路:按二进制位从高到低计算,假设所有 x i = 0 x_i=0 xi=0,此时只需考虑 y i y_i yi的上限,设 c c c为二进制第 k k k为 1 1 1的 y i y_i yi个数,则有
- c = 0 c=0 c=0,没有任何一个数第 k k k位为1,答案不变。
- c = 1 c=1 c=1,只有一个数第 k k k位为1,则答案加上 2 k 2^k 2k。
- c > 1 c>1 c>1,至少有2个数第 k k k位为1,因为下限 x i = 0 x_i=0 xi=0,所以我们可以将其中一个数的第 k k k位置为0,剩下的 k − 1 k-1 k−1位全置为1,即 2 k 2^k 2k变为 2 k − 1 2^k-1 2k−1,另一个数不变,则答案可以加上 2 k + ( 2 k − 1 ) 2^k+(2^k-1) 2k+(2k−1),则此时答案剩下的 k k k位已经全部变为1了,无需再向低位统计了。
所以我们只要去掉 x i x_i xi的限制,就可以利用前缀和统计每个二进制位1的个数,并根据上面规则算出最大答案。
如何去掉 x i x_i xi的限制呢,统计每对 ( x i , y i ) (x_i,y_i) (xi,yi)从高位到低位二进制的最长公共前缀值记为 w i w_i wi,并将 w i w_i wi从 ( x i , y i ) (x_i,y_i) (xi,yi)中减去变为 ( x i − w i , y i − w i ) (x_i-w_i,y_i-w_i) (xi−wi,yi−wi)即 ( x i ′ , y i ′ ) (x_i',y_i') (xi′,yi′),则此时就无需考虑 x i x_i xi的限制了,因为我们将 w i w_i wi从 ( x i , y i ) (x_i,y_i) (xi,yi)中减去以后,此时 y i ′ y_i' yi′最高位为 1 1 1, x i ′ x_i' xi′对应的最高位必为 0 0 0( y i ′ ≥ x i ′ + 1 y_i'\ge x_i'+1 yi′≥xi′+1),所以无论我们将 y i ′ y_i' yi′中的任何为 1 1 1的第 k k k位置为0,剩下的 k − 1 k-1 k−1位置为1,都能保证 y i ′ ≥ x i ′ y_i'\ge x_i' yi′≥xi′。
#include<bits/stdc++.h>
#define lson (k<<1)
#define rson (k<<1)+1
#define mid ((l+r)/2)
#define sz(x) int(x.size())
#define pii pair<ll,ll>
#define fi first
#define se second
using namespace std;
const int MAX=2e5+10;
const int MOD=998244353;
const int INF=1e9;
const double PI=acos(-1.0);
const double eps=1e-9;
typedef int64_t ll;
int s[30][MAX];
int c[30][MAX];
int solve()
{int n;scanf("%d",&n);for(int i=1;i<=n;i++){int x,y;scanf("%d%d",&x,&y);for(int j=29;j>=0;j--){s[j][i]=s[j][i-1];c[j][i]=c[j][i-1];if((y&(1<<j))==0)continue;if(x<((y>>j)<<j))c[j][i]++;else s[j][i]++;}}int q;scanf("%d",&q);while(q--){int x,y;scanf("%d%d",&x,&y);int ans=0;for(int i=29;i>=0;i--){int cnt=c[i][y]-c[i][x-1]+(s[i][y]-s[i][x-1]>0);if(cnt==1)ans|=1<<i;if(cnt>1){ans|=(2<<i)-1;break;}}printf("%d ",ans);}return puts("");
}
int main()
{int T;cin>>T;while(T--)solve();return 0;
}
相关文章:
)
Codeforces-1935E:Distance Learning Courses in MAC(思维)
E. Distance Learning Courses in MAC time limit per test 2 seconds memory limit per test 256 megabytes input standard input output standard output The New Year has arrived in the Master’s Assistance Center, which means it’s time to introduce a new feature…...

ZooKeeper和Diamond有什么不同
本文主要是讨论下两个类似产品:ZooKeeper和Diamond在配置管理这个应用场景上的异同点。 Diamond,顾名思义,寄寓了开发人员对产品稳定性的厚望,希望它像钻石一样,提供稳定的配置访问。Diamond是淘宝网Java中间件团队的核…...
三、N元语法(N-gram)
为了弥补 One-Hot 独热编码的维度灾难和语义鸿沟以及 BOW 词袋模型丢失词序信息和稀疏性这些缺陷,将词表示成一个低维的实数向量,且相似的词的向量表示是相近的,可以用向量之间的距离来衡量相似度。 N-gram 统计语言模型是用来计算句子概率的…...

QML 3D入门知识路线
目前使用的版本 v5.14.0 模块导入 使用QML 3D时需要 import Qt3D.Core 2.14 核心模块类 V6以上的版本已经发布,所以有很多module会发生变化,主要有核心module、输入、逻辑、渲染、动画和扩展module,以及2D/3D场景模块 类名 能…...
)
蓝牙系列五:开源蓝牙协议BTStack框架代码阅读(1)
蓝牙学习系列,借鉴卫东上老师的蓝牙视频教程。 BTStack协议栈学习。首先来看一下,对于硬件操作,它是如何来进行处理的。在上篇文章中曾说过,在main函数里面它会调用硬件相关的代码,调用操作系统相关的代码。在BTStack中,可以搜索一下main.c,将会发现有很多main.c,都是…...

c++ 类内可以定义引用数据成员吗?
在C中,类内是可以定义引用数据成员的,但是在初始化对象时,必须在构造函数的成员初始化列表中对引用进行初始化,因为引用必须在创建时被初始化,并且不能在其生存期内引用不同的对象。下面是一个简单的示例: …...
MacBook2024苹果免费mac电脑清理垃圾软件CleanMyMac X
CleanMyMac X是一款专业的Mac清理软件,具备多种强大功能。首先,它能够智能清理Mac磁盘上的垃圾文件和多余语言安装包,从而快速释放电脑内存。其次,CleanMyMac X可以轻松管理和升级Mac上的应用,同时强力卸载恶意软件并修…...

Vue.js计算属性:实现数据驱动的利器
🤍 前端开发工程师、技术日更博主、已过CET6 🍨 阿珊和她的猫_CSDN博客专家、23年度博客之星前端领域TOP1 🕠 牛客高级专题作者、打造专栏《前端面试必备》 、《2024面试高频手撕题》 🍚 蓝桥云课签约作者、上架课程《Vue.js 和 E…...
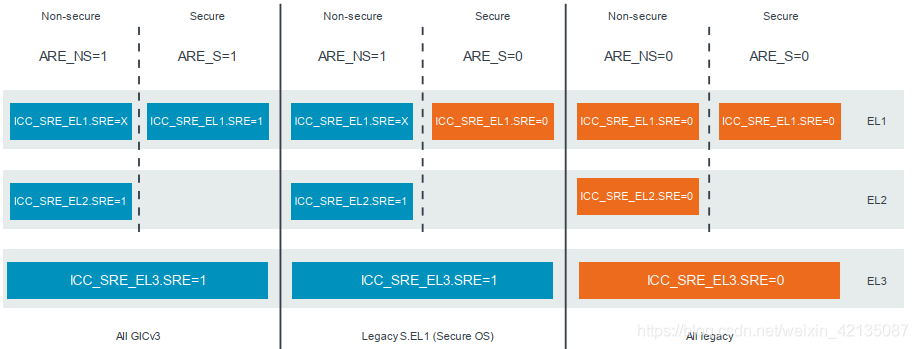
10-ARM gicv3/gicv4的总结-基础篇
目录 1、gic的版本2、GICv3/gicv4的模型图3、gic中断号的划分4、GIC连接方式5、gic的状态6、gic框架7、gic Configuring推荐 本文转自 周贺贺,baron,代码改变世界ctw,Arm精选, armv8/armv9,trustzone/tee,s…...

数据库系统概论(超详解!!!) 第三节 关系数据库
1.基本概念 1. 域(Domain) 域是一组具有相同数据类型的值的集合。 2. 笛卡尔积(Cartesian Product) 给定一组域D1,D2,…,Dn,允许其中某些域是相同的。 D1,D2…...
Springboot 集成kafka 消费者实现ssl方式连接监听消息实现消费
证书准备:springboot集成kafka 消费者实现 如何配置是ssl方式连接的时候需要进行证书的转换。原始的证书是pem, 或者csr方式 和key方式的时候需要转换,因为kafka里面是jks 需要通过openssl进行转换。 证书处理: KeyStore 用于存储客户端的证…...
spark 实验二 RDD编程初级实践
目录 一. pyspark交互式编程示例(学生选课成绩统计) 该系总共有多少学生; 该系DataBase课程共有多少人选修; 各门课程的平均分是多少; 使用累加器计算共有多少人选了DataBase这门课。 二.编写独立应用程序实现数…...
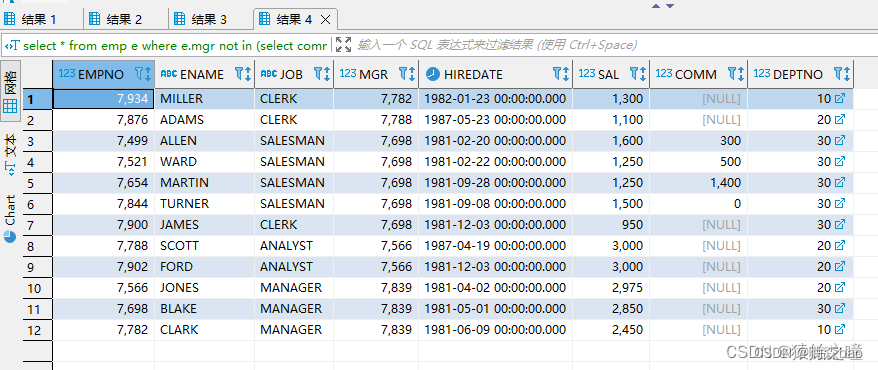
【MySQL】not in遇上null的坑
今天遇到一个问题: 1、当 in 内的字段包含 null 的时候,正常过滤; 2、当 not in 内的字段包含 null 的时候,不能正常过滤,即使满足条件,最终结果也为 空。 测试如下: select * from emp e;当…...

鸿蒙4.0-DevEco Studio界面工程
DevEco Studio界面工程 DevEco Studio 下载与第一个工程新建的第一个工程界面回到Project工程结构来看 DevEco Studio 下载与第一个工程 DevEco Studio 下载地址:点击跳转 https://developer.harmonyos.com/cn/develop/deveco-studio#download 学习课堂以及文档地址…...
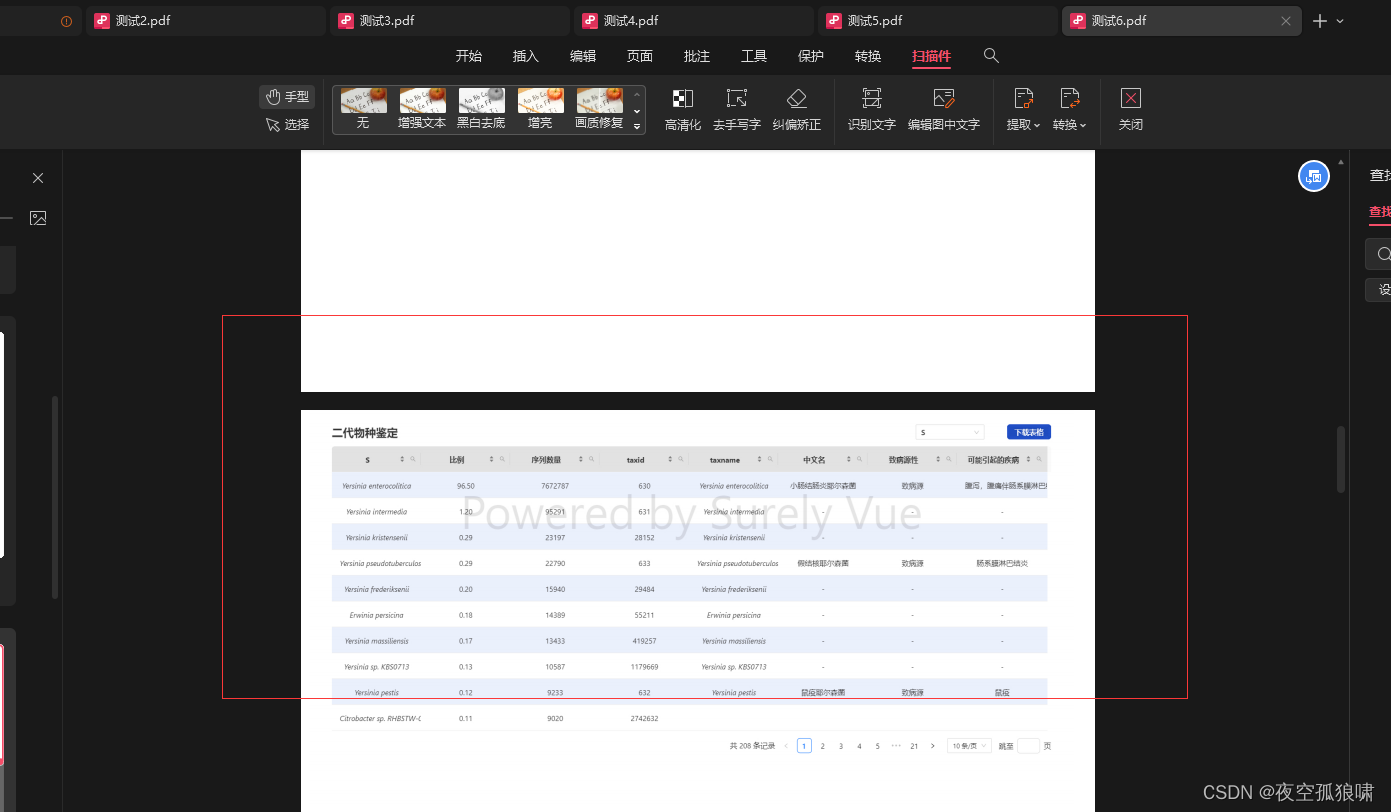
前端将html导出pdf文件解决分页问题
这是借鉴了qq_251025116大佬的解决方案并优化升级完成的,原文链接 1.安装依赖 npm install jspdf html2canvas2.使用方法 import htmlToPdffrom ./index.jsconst suc () > {message.success(success);};//记得在需要打印的div上面添加 idlet dom document.que…...
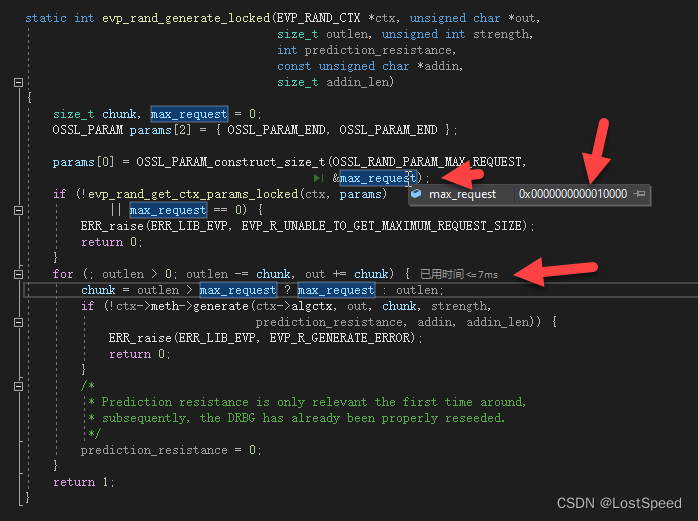
openssl3.2 - exp - 产生随机数
文章目录 openssl3.2 - exp - 产生随机数概述笔记END openssl3.2 - exp - 产生随机数 概述 要用到openssl产生的随机数, 查了资料. 如果用命令行产生随机数, 如下: openssl rand -hex -num 6 48bfd3a64f54单步跟进去, 看到主要就是调用了一个RAND_bytes(), 没其他了. 官方说…...
[]有何不同?)
【三两波折】char *foo[]和char(*foo)[]有何不同?
1、先谈优先级 最高级别 —— 有四个,他们并不像运算符: []数组下标左到右结合()用于(表达式) or 函数名(形参表)左到右结合.读取结构体成员左到右结合->读取结构体成员(通过指针)左到右结合 第二级别…...
怎么查看pod服务对应哪些docker容器)
k8s(kubernetes)怎么查看pod服务对应哪些docker容器
Kubernetes(k8s)中的Pod是一组共享网络和存储资源的容器集合。每个Pod都包含一个或多个Docker容器,这些容器共享网络命名空间和存储卷,并在同一主机上运行。因此,可以将Pod视为一组紧密相关的Docker容器的逻辑主机&…...
)
[2023年]-hadoop面试真题(二)
[2023年]-hadoop面试真题(一) (北京) Maptask的个数由什么决定?(北京) 如何判定一个job的map和reduce的数量 ?(北京) MR中Shuffle过程 ?(北京) MR中处理数据流程 ?(…...
蓝桥杯备战刷题-滑动窗口
今天给大家带来的是滑动窗口的类型题,都是十分经典的。 1,无重复字符的最长子串 看例三,我们顺便来说一下子串和子序列的含义 子串是从字符串里面抽出来的一部分,不可以有间隔,顺序也不能打乱。 子序列也是从字符串里…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...
