数据库系统概论(超详解!!!) 第三节 关系数据库
1.基本概念
1. 域(Domain)
域是一组具有相同数据类型的值的集合。
2. 笛卡尔积(Cartesian Product)
给定一组域D1,D2,…,Dn,允许其中某些域是相同的。
D1,D2,…,Dn的笛卡尔积为: D1×D2×…×Dn = {(d1,d2,…,dn)|diDi,i=1,2,…,n}
所有域的所有取值的一个组合 ,不能重复。
元组(Tuple) 笛卡尔积中每一个元素(d1,d2,…,dn)叫作一个n元组(n-tuple)或简称元组
分量(Component) 笛卡尔积元素(d1,d2,…,dn)中的每一个值di 叫作一个分量 。
基数(Cardinal number) 一个域允许的不同取值个数称为这个域的基数。 若Di(i=1,2,…,n)为有限集,其基数为mi(i=1,2,…,n),则D1×D2×…×Dn的基数M为:
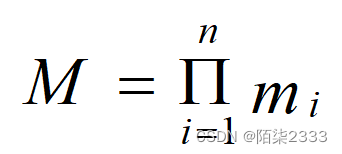
笛卡尔积的表示方法 :笛卡尔积可表示为一张二维表, 表中的每行对应一个元组,表中的每列对应一个域。
3. 关系(Relation)
D1×D2×…×Dn的子集叫作在域D1,D2,…, Dn上的关系,表示为R(D1,D2,…,Dn)
R:关系名
n:关系的目或度(Degree)
元组: 关系中的每个元素是关系中的元组,通常用t表示。
单元关系与二元关系:
当n=1时,称该关系为单元关系(Unary relation)或一元关系
当n=2时,称该关系为二元关系(Binary relation)
关系的表示:关系也是一个二维表,表的每行对应一个元组,表 的每列对应一个域.
属性 :关系中不同列可以对应相同的域 ,为了加以区分,必须对每列起一个名字,称为属性(Attribute) 。n目关系必有n个属性。
码 :
候选码(Candidate key) 若关系中的某一属性组的值能唯一地标识一个元组,则称该属性组为候选码。 简单的情况:候选码只包含一个属性。
全码(All-key) 最极端的情况:关系模式的所有属性组是这个关系模式的候选码,称为全码(All-key)
主码 :若一个关系有多个候选码,则选定其中一个为主码 (Primary key)
主属性: 候选码中的属性称为主属性(Prime attribute) 不包含在任何侯选码中的属性称为非主属性(Non-Prime attribute)或非码属性(Non-key attribute)
三类关系:
基本关系(基本表或基表) :实际存在的表,是实际存储数据的逻辑表示
查询表查:询结果对应的表
视图表 :由基本表或其他视图表导出的表,是虚表,不对 应实际存储的数据。
基本关系的性质:
① 列是同质的(Homogeneous)
② 不同的列可出自同一个域 ,其中的每一列称为一个属性 ,不同的属性要给予不同的属性名。
③ 列的顺序无所谓,列的次序可以任意交换
④ 任意两个元组的候选码不能相同
⑤ 行的顺序无所谓,行的次序可以任意交换
⑥ 分量必须取原子值 ,这是规范条件中最基本的一条
4.关系模式
关系模式(Relation Schema)是型 。
关系是值。
关系模式是对关系的描述:元组集合的结构 ,属性构成 ,属性来自的域,属性与域之间的映象关系 。完整性约束条件。
关系模式可以形式化地表示为: R(U,D,DOM,F)
R:关系名
U:组成该关系的属性名集合
D:U中属性所来自的域
DOM:属性向域的映象集合
F :属性间数据的依赖关系的集合
关系模式通常可以简记为 :R (U) 或 R (A1,A2,…,An)
R: 关系名
A1,A2,…,An : 属性名
注:域名及属性向域的映象常常直接说明为属性的类型、长度。
关系模式 :对关系的描述 。静态的、稳定的
关系 :关系模式在某一时刻的状态或内容 动态的、随时间不断变化的 。
关系模式和关系往往笼统称为关系
5.关系数据库
关系数据库:在一个给定的应用领域中,所有关系的集合构成一个关系数据库。
关系数据库的型与值 :
关系数据库的型: 关系数据库模式,是对关系数据库的描述。
关系数据库的值: 关系模式在某一时刻对应的关系的集合,通常称为关系数据库。
6.关系模型的存储结构
关系数据库的物理组织 :有的关系数据库管理系统中一个表对应一个操作系统文件,将物理数据组织交给操作系统完成。 有的关系数据库管理系统从操作系统那里申请若干个大的文件,自己划分文件空间,组织表、索引等存储结构,并进行存储管理。
2.关系操作
1.常用的关系操作
查询操作:选择、投影、连接、除、并、差、交、笛卡尔积。
选择、投影、并、差、笛卡尔是5种基本操作
数据更新:插入、删除、修改。
关系操作的特点:集合操作方式:操作的对象和结果都是集合,一次一集合的方式。
2.语言的分类
关系代数语言: 用对关系的运算来表达查询要求 。 代表:ISBL
关系演算语言:
用谓词来表达查询要求: 元组关系演算语言 。谓词变元的基本对象是元组变量。 代表:APLHA, QUEL
域关系演算语言 : 谓词变元的基本对象是域变量 。 代表:QBE
具有关系代数和关系演算双重特点的语言。 代表:SQL(Structured Query Language)
3.关系的完整性
1.实体完整性
关系的三类完整性约束:
1.实体完整性和参照完整性: 关系模型必须满足的完整性约束条件称为关系的两个不变性,应该由关系系统自动支持。
2.用户定义的完整性 :应用领域需要遵循的约束条件,体现了具体领域中的语义约束。
实体完整性规则(Entity Integrity)
若属性A是基本关系R的主属性,则属性A不能取空值 。空值就是“不知道”或“不存在”或“无意义”的值。
实体完整性规则的说明 :
(1)实体完整性规则是针对基本关系而言的。 一个基本表通常对应现实世界的一个实体集。
(2)现实世界中的实体是可区分的,即它们具有某种唯一性标识。
(3)关系模型中以主码作为唯一性标识。
(4)主码中的属性即主属性不能取空值。 主属性取空值,就说明存在某个不可标识的实体,即存在不可区分的实体,这与第(2)点相矛盾,因此这个规则称为实体完整性。
2.参照完整性
1. 关系间的引用
在关系模型中实体及实体间的联系都是用关系来描述的,自然存在着关系与关系间的引用。
2. 外码
设F是基本关系R的一个或一组属性,但不是关系R的码。如果F与基本关系S的主码Ks相对应,则称F是R的外码
基本关系R称为参照关系(Referencing Relation)
基本关系S称为被参照关系(Referenced Relation) 或目标关系(Target Relation)
注:
关系R和S不一定是不同的关系。
目标关系S的主码Ks 和参照关系的外码F必须定义在同一个(或一组)域上。
外码并不一定要与相应的主码同名。
当外码与相应的主码属于不同关系时,往往取相同的名字,以便于识别。


3. 参照完整性规则
参照完整性规则 :
若属性(或属性组)F是基本关系R的外码,它与基本关系S的主码Ks相对应(基本关系R和S不一定是不同的关系),则对于R中每个元组在F上的值必须为: 或者取空值(F的每个属性值均为空值) ,或者等于S中某个元组的主码值。
3.用户定义的完整性
针对某一具体关系数据库的约束条件,反映某一具体应用所涉及的数据必须满足的语义要求
关系模型应提供定义和检验这类完整性的机制,以便用统一的系统的方法处理它们,而不需由应用程序承担这一功能
4.关系代数
关系代数是一种抽象的查询语言,它用对关系的运算来表达查询
关系代数: 运算对象是关系 ,运算结果亦为关系 。
关系代数的运算符有两类:集合运算符和专门的关系运算符 。传统的集合运算是从关系的“水平”方向即行的角度进行 ,专门的关系运算不仅涉及行而且涉及列。
1.传统集合运算
R和S 具有相同的目n(即两个关系都有n个属性) 相应的属性取自同一个域(以下没显示出来的符号为”属于“)
R∪S 仍为n目关系,由属于R或属于S的元组组成。 R∪S = { t|t R∨t S }
R - S 仍为n目关系,由属于R而不属于S的所有元组组成。 R -S = { t|tR∧tS }
R∩S 仍为n目关系,由既属于R又属于S的元组组成。R∩S = { t|t R∧t S } R∩S = R –(R-S)



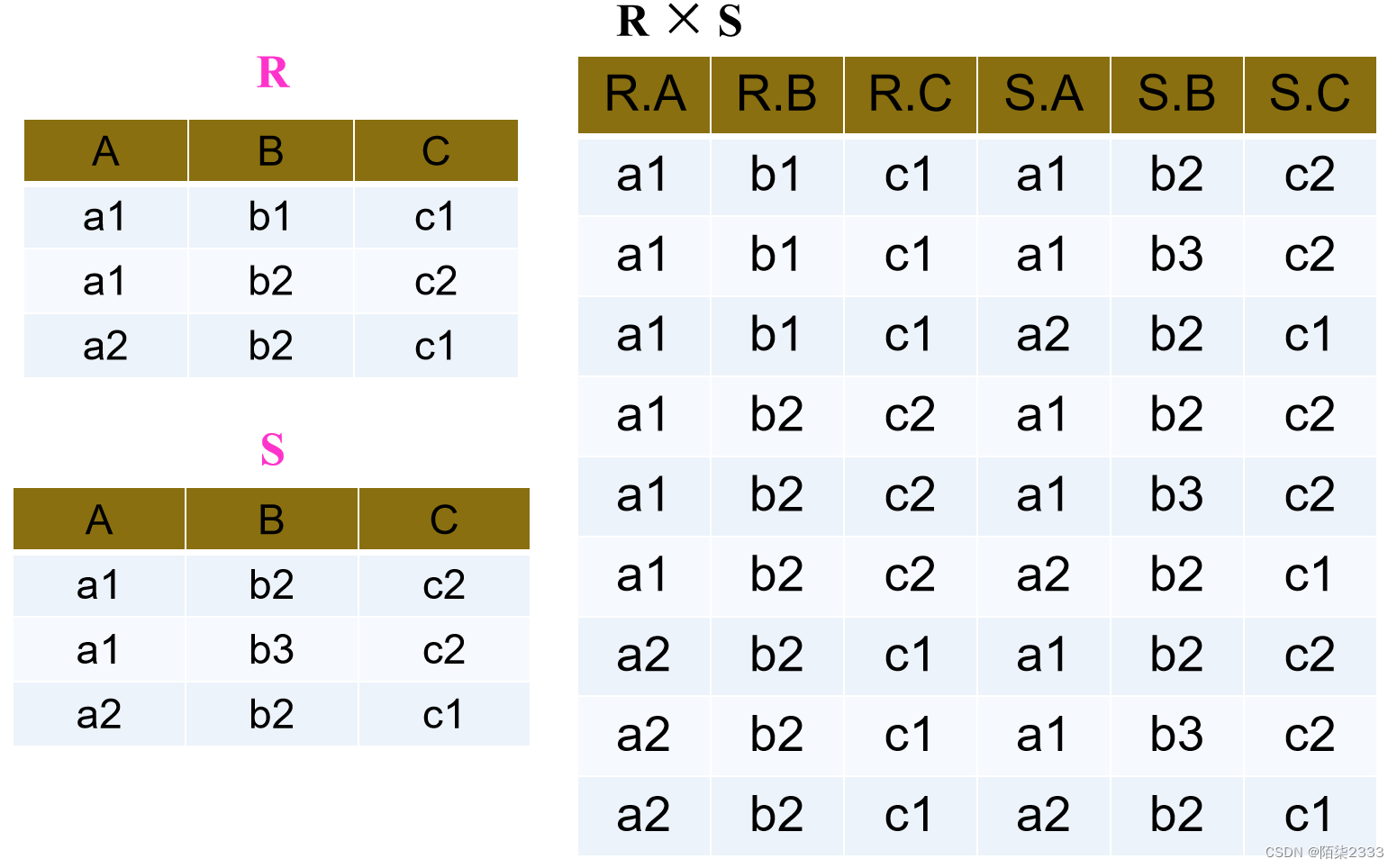
笛卡尔积:
严格地讲应该是广义的笛卡尔积(Extended Cartesian Product)
R: n目关系,k1个元组
S: m目关系,k2个元组
R×S
列:(n+m)列元组的集合
元组的前n列是关系R的一个元组 ,后m列是关系S的一个元组
行:k1×k2个元组 R×S = {tr ts |tr R ∧ tsS }
2.专门关系运算
引入新的表示方法:
(1) R,t属于R,t[Ai]
设关系模式为R(A1,A2,…,An) 它的一个关系设为R ,t属于R 表示t是R的一个元组 ,t[Ai]则表示元组t中相应于属性Ai的一个分量。
(2) A,t[A], A非
若A={Ai1,Ai2,…,Aik},其中Ai1,Ai2,…,Aik是A1,A2,…,An中的一部分,则A称为属性列或属性组。
t[A]=(t[Ai1],t[Ai2],…,t[Aik])表示元组t在属性列A上诸分量的集合。
A非则表示{A1,A2,…,An}中去掉{Ai1,Ai2,…,Aik}后剩余的属性组。

(4)象集Zx
给定一个关系R(X,Z),X和Z为属性组。当t[X]=x时,x在R中的象集(Images Set)为: Zx={t[Z]|t R,t[X]=x} 它表示R中属性组X上值为x的诸元组在Z上分量的集合。

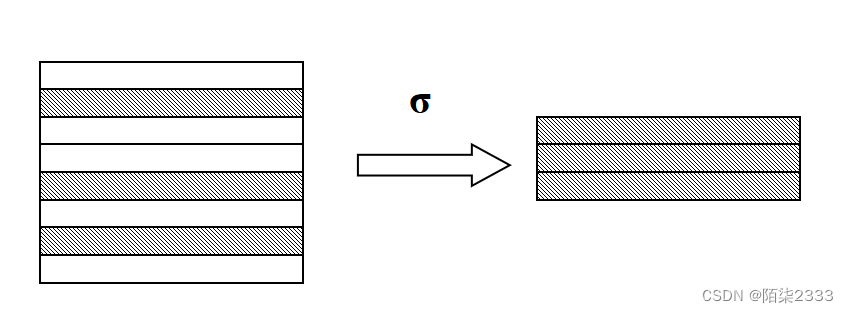
1. 选择
选择又称为限制(Restriction)选择运算符的含义在关系R中选择满足给定条件的诸元组 σF(R) = {t|t属于R∧F(t)= '真'}
F:选择条件,是一个逻辑表达式,取值为“真”或“假” 基本形式为:X1θY1
θ表示比较运算符,它可以是>,≥,<,≤,=或<>
选择运算是从关系R中选取使逻辑表达式F为真的元组,是从行的角度进行的运算
2. 投影
从R中选择出若干属性列组成新的关系 : πA(R) = { t[A] | t 属于R }
A:R中的属性列
投影操作主要是从列的角度进行运算

投影之后不仅取消了原关系中的某些列,而且还可能取消某些元组(避免重复行)
3. 连接
连接也称为θ连接 ,连接运算的含义: 从两个关系的笛卡尔积中选取属性间满足一定条件的元组

A和B:分别为R和S上度数相等且可比的属性组
θ:比较运算符
连接运算从R和S的广义笛卡尔积R×S中选取R关系在A属性组上的值与S关系在B属性组上的值满足比较关系θ的元组
两类常用连接运算 :
等值连接(equijoin) θ为“=”的连接运算称为等值连接,从关系R与S的广义笛卡尔积中选取A、B属性值相等的那些元组,即等值连接为:

自然连接(Natural join)
自然连接是一种特殊的等值连接,两个关系中进行比较的分量必须是同名的属性组 ,在结果中把重复的属性列去掉
自然连接的含义 :R和S具有相同的属性组B

一般的连接操作是从行的角度进行运算。

自然连接还需要取消重复列,所以是同时从行和列的角度进行运算。
注:两个关系在没有公共属性时,其自然连接操作表现为笛卡尔积操作。




悬浮元组(Dangling tuple): 两个关系R和S在做自然连接时,关系R中某些元组有可能在S中不存在公共属性上值相等的元组,从而造成R中这些元组在操作时被舍弃了,这些被舍弃的元组称为悬浮元组。
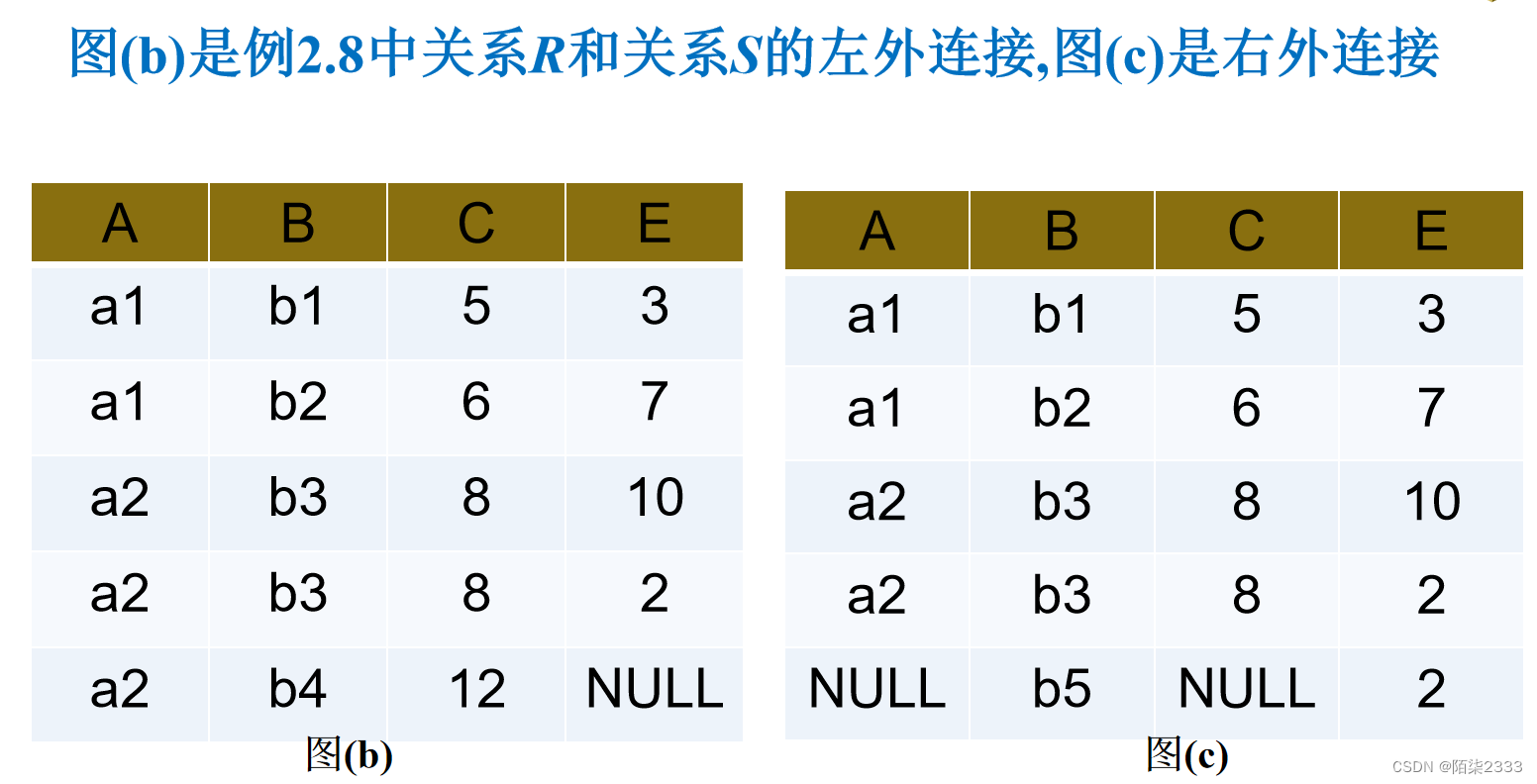
外连接(Outer Join): 如果把悬浮元组也保存在结果关系中,而在其他属性上填空值(Null),就叫做外连接
左外连接(LEFT OUTER JOIN或LEFT JOIN) 只保留左边关系R中的悬浮元组。
右外连接(RIGHT OUTER JOIN或RIGHT JOIN) 只保留右边关系S中的悬浮元组。

4. 除运算
给定关系R (X,Y) 和S (Y,Z),其中X,Y,Z为属性组。 R中的Y与S中的Y可以有不同的属性名,但必须出自相同的域集。
R与S的除运算得到一个新的关系P(X), P是R中满足下列条件的元组在 X 属性列上的投影: 元组在X上分量值x的象集Yx包含S在Y上投影的集合,记作:
R÷S={tr[X]|trR∧πY(S)属于Yx} Yx:x在R中的象集,x = tr[X]
从行和列的角度考虑:


在关系R中,A可以取四个值{a1,a2,a3,a4}
a1的象集为 {(b1,c2),(b2,c3),(b2,c1)}
a2的象集为 {(b3,c7),(b2,c3)}
a3的象集为 {(b4,c6)}
a4的象集为 {(b6,c6)}
S在(B,C)上的投影为:{(b1,c2),(b2,c1),(b2,c3) }
只有a1的象集包含了S在(B,C)属性组上的投影,所以 R÷S ={a1}
注意:关系运算中花费时间可能最长的运算是笛卡尔积
例题:


小结:
关系数据库系统是目前使用最广泛的数据库系统
关系数据库系统与非关系数据库系统的区别: 关系系统只有“表”这一种数据结构 非关系数据库系统还有其他数据结构,以及对这些数据结构的操作。
相关文章:

数据库系统概论(超详解!!!) 第三节 关系数据库
1.基本概念 1. 域(Domain) 域是一组具有相同数据类型的值的集合。 2. 笛卡尔积(Cartesian Product) 给定一组域D1,D2,…,Dn,允许其中某些域是相同的。 D1,D2…...
Springboot 集成kafka 消费者实现ssl方式连接监听消息实现消费
证书准备:springboot集成kafka 消费者实现 如何配置是ssl方式连接的时候需要进行证书的转换。原始的证书是pem, 或者csr方式 和key方式的时候需要转换,因为kafka里面是jks 需要通过openssl进行转换。 证书处理: KeyStore 用于存储客户端的证…...
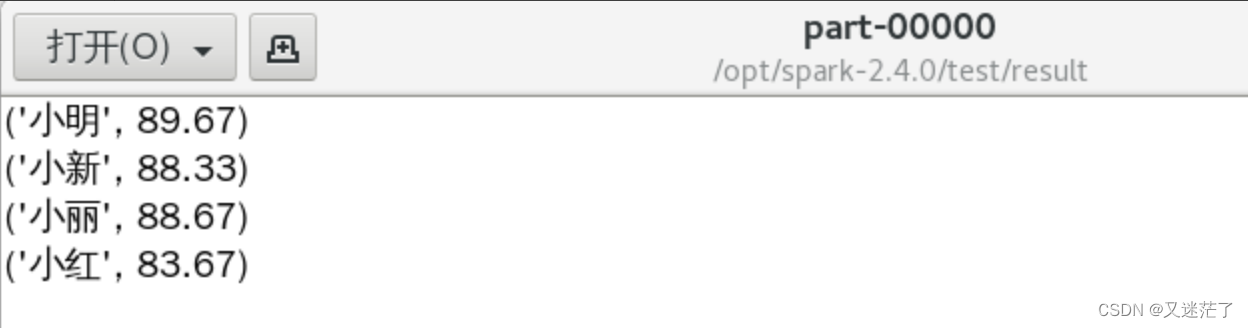
spark 实验二 RDD编程初级实践
目录 一. pyspark交互式编程示例(学生选课成绩统计) 该系总共有多少学生; 该系DataBase课程共有多少人选修; 各门课程的平均分是多少; 使用累加器计算共有多少人选了DataBase这门课。 二.编写独立应用程序实现数…...
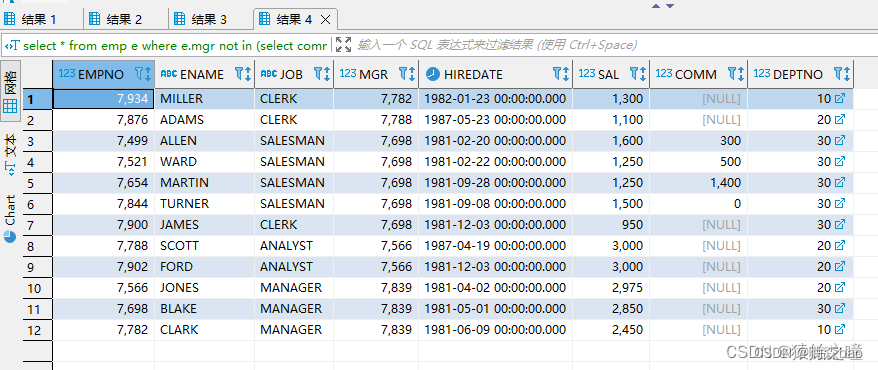
【MySQL】not in遇上null的坑
今天遇到一个问题: 1、当 in 内的字段包含 null 的时候,正常过滤; 2、当 not in 内的字段包含 null 的时候,不能正常过滤,即使满足条件,最终结果也为 空。 测试如下: select * from emp e;当…...

鸿蒙4.0-DevEco Studio界面工程
DevEco Studio界面工程 DevEco Studio 下载与第一个工程新建的第一个工程界面回到Project工程结构来看 DevEco Studio 下载与第一个工程 DevEco Studio 下载地址:点击跳转 https://developer.harmonyos.com/cn/develop/deveco-studio#download 学习课堂以及文档地址…...
前端将html导出pdf文件解决分页问题
这是借鉴了qq_251025116大佬的解决方案并优化升级完成的,原文链接 1.安装依赖 npm install jspdf html2canvas2.使用方法 import htmlToPdffrom ./index.jsconst suc () > {message.success(success);};//记得在需要打印的div上面添加 idlet dom document.que…...
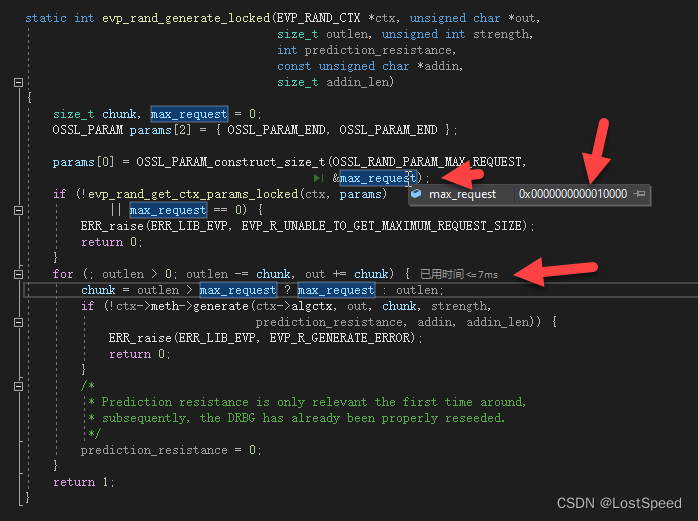
openssl3.2 - exp - 产生随机数
文章目录 openssl3.2 - exp - 产生随机数概述笔记END openssl3.2 - exp - 产生随机数 概述 要用到openssl产生的随机数, 查了资料. 如果用命令行产生随机数, 如下: openssl rand -hex -num 6 48bfd3a64f54单步跟进去, 看到主要就是调用了一个RAND_bytes(), 没其他了. 官方说…...
[]有何不同?)
【三两波折】char *foo[]和char(*foo)[]有何不同?
1、先谈优先级 最高级别 —— 有四个,他们并不像运算符: []数组下标左到右结合()用于(表达式) or 函数名(形参表)左到右结合.读取结构体成员左到右结合->读取结构体成员(通过指针)左到右结合 第二级别…...
怎么查看pod服务对应哪些docker容器)
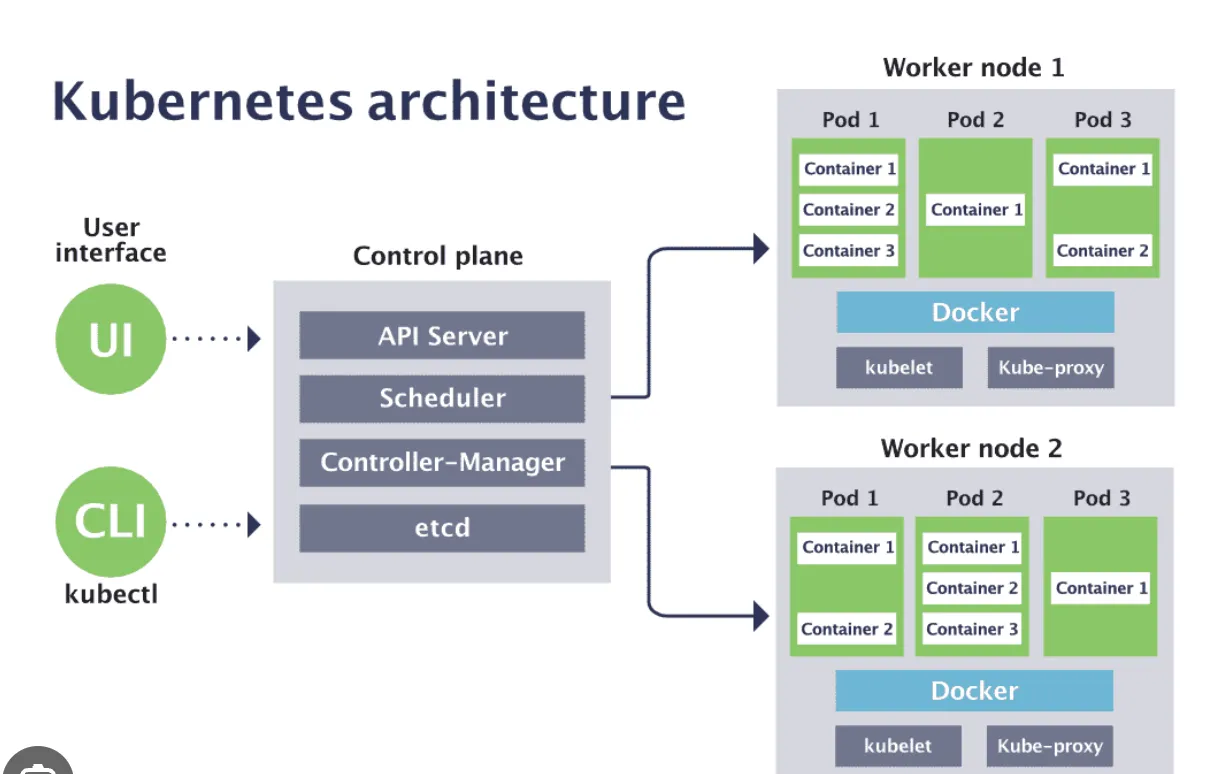
k8s(kubernetes)怎么查看pod服务对应哪些docker容器
Kubernetes(k8s)中的Pod是一组共享网络和存储资源的容器集合。每个Pod都包含一个或多个Docker容器,这些容器共享网络命名空间和存储卷,并在同一主机上运行。因此,可以将Pod视为一组紧密相关的Docker容器的逻辑主机&…...
)
[2023年]-hadoop面试真题(二)
[2023年]-hadoop面试真题(一) (北京) Maptask的个数由什么决定?(北京) 如何判定一个job的map和reduce的数量 ?(北京) MR中Shuffle过程 ?(北京) MR中处理数据流程 ?(…...
蓝桥杯备战刷题-滑动窗口
今天给大家带来的是滑动窗口的类型题,都是十分经典的。 1,无重复字符的最长子串 看例三,我们顺便来说一下子串和子序列的含义 子串是从字符串里面抽出来的一部分,不可以有间隔,顺序也不能打乱。 子序列也是从字符串里…...
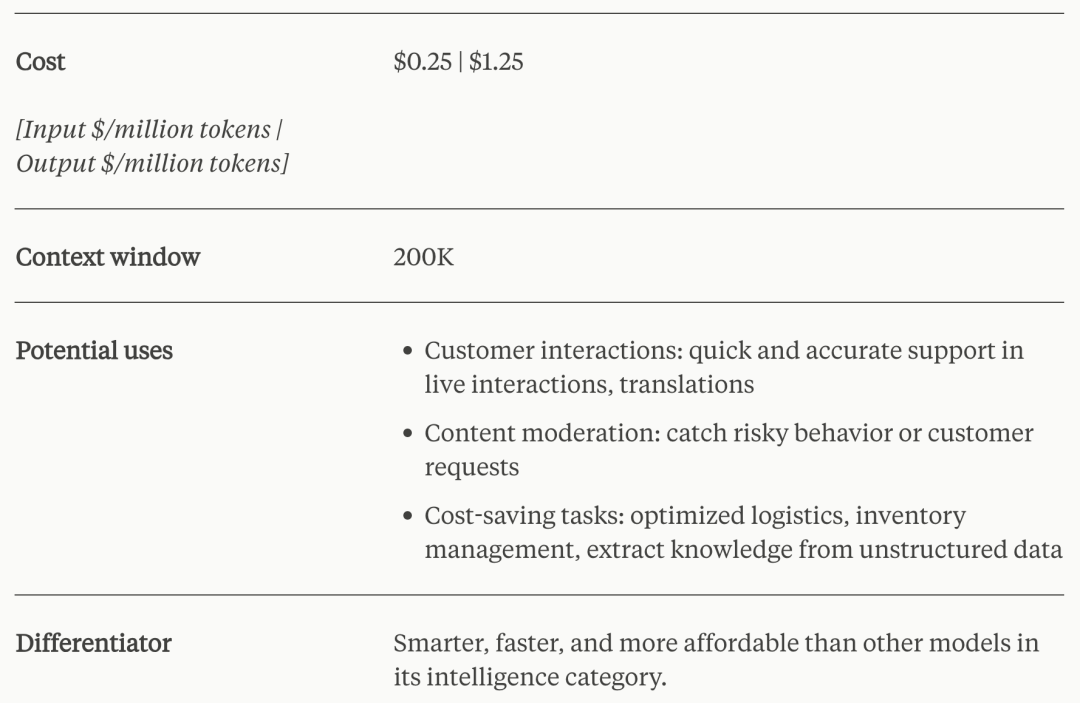
LLM(十一)| Claude 3:Anthropic发布最新超越GPT-4大模型
2024年3月4日,Anthropic发布最新多模态大模型:Claude 3系列,共有Haiku、Sonnet和Opus三个版本。 Opus在研究生水平专家推理、基础数学、本科水平专家知识、代码等10个维度,超过OpenAI的GPT-4。 Haiku模型更注重效率,能…...
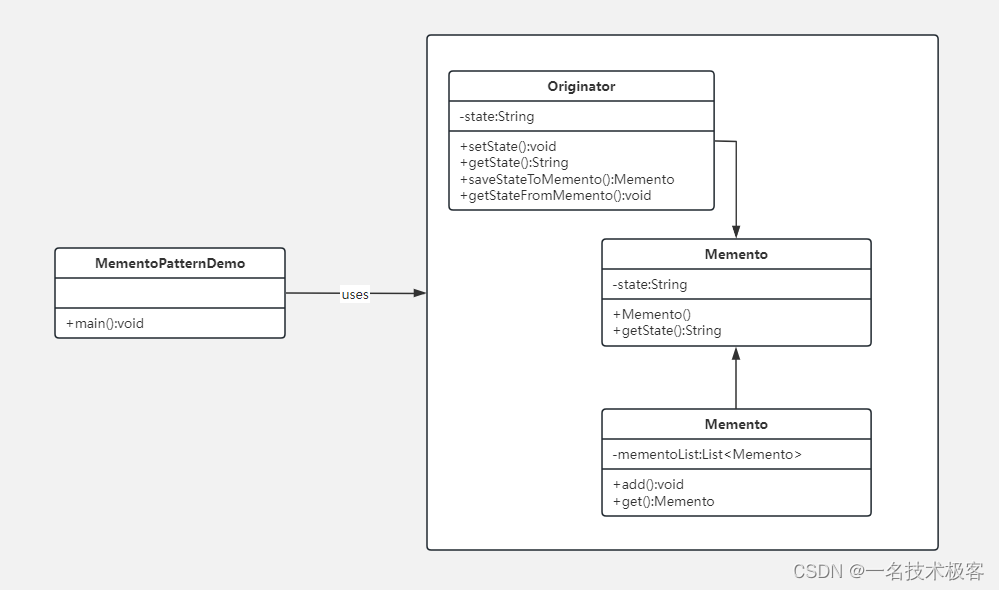
20-Java备忘录模式 ( Memento Pattern )
Java备忘录模式 摘要实现范例 备忘录模式(Memento Pattern)保存一个对象的某个状态,以便在适当的时候恢复对象 备忘录模式属于行为型模式 摘要 1. 意图 在不破坏封装性的前提下,捕获一个对象的内部状态,并在该对…...

整合生成型AI战略:从宏观思维到小步实践
“整合生成型AI战略:从宏观思维到小步实践” 在这篇文章中,我们探讨了将生成型AI和大型语言模型融入企业核心业务的战略开发方法。我们的方法基于敏捷开发原则,技术专家和数据科学家需要采纳商业思维,而执行官则需理解生成型AI和…...
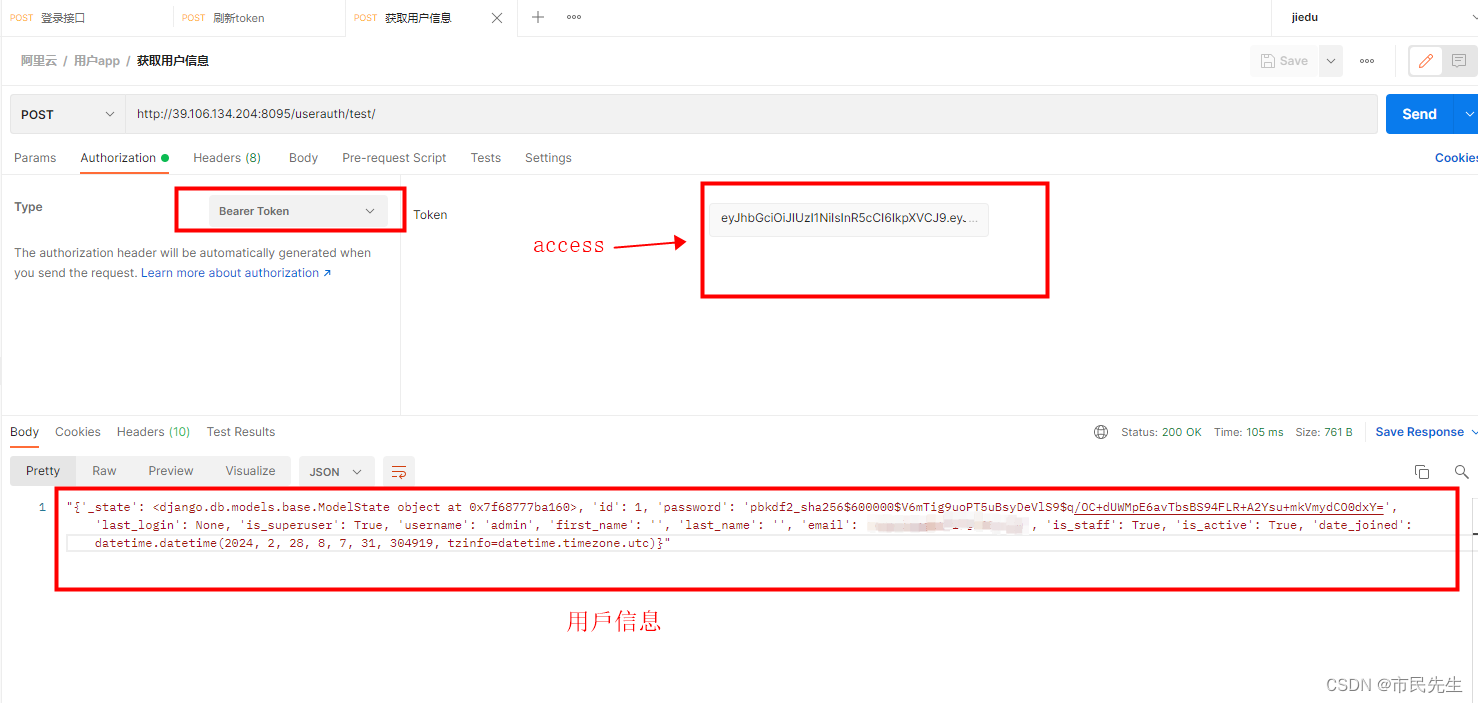
个人博客系列-后端项目-用户验证(5)
介绍 创建系统管理app,用于管理系统的用户,角色,权限,登录等功能,项目中将使用django-rest_framework进行用户认证和权限解析。这里将完成用户认证 用户验证 rest_framework.authentication模块中的认证类ÿ…...
css3中nth-child属性作用及用法剖析
hello宝子们...我们是艾斯视觉擅长ui设计和前端开发10年经验!希望我的分享能帮助到您!如需帮助可以评论关注私信我们一起探讨!致敬感谢感恩! 标题:CSS3中nth-child属性作用及用法剖析 摘要:CSS3中的nth-child选择器允许我们根据元素位置来定位特定的元素…...

okHttp MediaType MIME格式详解
一、介绍 我们在做数据上传时,经常会用到Okhttp的开源库,okhttp开源库也遵循html提交的MIME数据格式。 所以我们经常会看到applicaiton/json这样的格式在传。 但是如果涉及到其他文件等就需要详细的数据格式,否则服务端无法解析 二、okHt…...

跨境电商三大趋势
跨境电商有着不断发展的三大趋势: 个性化定制:随着消费者需求的不断变化和个性化定制的潮流,跨境电商平台开始提供更多的定制化服务。消费者可以根据自己的需求选择产品的款式、材料和设计,从而获得更加个性化的产品体验。 无界销…...
【DevOps基础篇之k8s】如何通过Kubernetes CKA认证考试
【DevOps基础篇之k8s】如何通过Kubernetes CKA认证考试 目录 【DevOps基础篇之k8s】如何通过Kubernetes CKA认证考试核心概念资源监控生命周期管理Cluster维护安全认证问题排查其他推荐超级课程: Docker快速入门到精通Kubernetes入门到大师通关课这些是我在准备CK...

Mysql数据库-基本表操作
1.表操作 创建表:CREATE TABLE table_name ( field1 datatype, field2 datatype, field3 datatype ) character set 字符集 collate 校验规则 engine 存储引擎; field 表示列名 datatype 表示列的类型 character set 字符集,如果没有指定字符集ÿ…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...
