算法学习之动态规划DP——背包问题
一、01背包问题
(一)题目
有 N 件物品和一个容量是 V的背包。每件物品只能使用一次。
第i件物品的体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式
第一行两个整数,N,V,用空格隔开,分别表示物品数量和背包容积。
接下来有 N行,每行两个整数 vi,wi,用空格隔开,分别表示第i件物品的体积和价值。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N,V≤1000
0<vi,wi≤1000
输入样例
4 5
1 2
2 4
3 4
4 5
输出样例:
8
(二 )题解
【一】 二维动态规划
(1)状态f[i][j]定义:前 i 个物品,背包容量 j下的最优解(最大价值):
当前的状态依赖于之前的状态,可以理解为从初始状态f[0][0] = 0开始决策,有 N
件物品,则需要 N 次决 策,每一次对第 i件物品的决策,状态f[i][j]不断由之前的状态更新而来。
(2)当前背包容量不够(j < v[i]),没得选,因此前 i个物品最优解即为前 i−1个物品最优解:
对应代码:f[i][j] = f[i - 1][j]。
(3)当前背包容量够,可以选,因此需要决策选与不选第i个物品:
选:f[i][j] = f[i - 1][j - v[i]] + w[i]。
不选:f[i][j] = f[i - 1][j] 。
我们的决策是如何取到最大价值,因此以上两种情况取 max() 。
对应代码
#include<iostream>
#include<cstdio>
#include<cstring>using namespace std;const int N = 1010;int v[N], w[N];
int f[N][N];int n, m;int main(){scanf("%d%d", &n, &m);for(int i = 1; i <= n; ++ i) scanf("%d%d", &v[i], &w[i]);for(int i = 1; i <= n; ++ i){for(int j = 0; j <= m; ++ j){f[i][j] = f[i-1][j];if(j >= v[i]) f[i][j] = max(f[i][j], f[i-1][j-v[i]]+w[i]);}}printf("%d", f[n][m]);return 0;
}【二】优化:状态压缩(二维变一维)
将状态f[i][j]优化到一维f[j],实际上只需要做一个等价变形。
为什么可以这样变形呢?我们定义的状态f[i][j]可以求得任意合法的i与j最优解,但题目只需要求得最终状态f[n][m],因此我们只需要一维的空间来更新状态。
(1)状态f[j]定义:N件物品,背包容量j下的最优解。
(2)注意枚举背包容量j必须从m开始。
为什么一维情况下枚举背包容量需要逆序?在二维情况下,状态f[i][j]是由上一轮i - 1的状态得来的,f[i][j]与f[i - 1][j]是独立的。而优化到一维后,如果我们还是正序,则有f[较小体积]更新到f[较大体积],则有可能本应该用第i-1轮的状态却用的是第i轮的状态。
例如,一维状态第i轮对体积为 3的物品进行决策,则f[7]由f[4]更新而来,这里的f[4]正确应该f[i-1][4],但从小到大枚举j这里的f[4]在第i轮计算却变成了f[i][4]。当逆序枚举背包容量j时,我们求f[7]同样由f[4]更新,但由于是逆序,这里的f[4]还没有在第i轮计算,所以此时实际计算的f[4]仍然是f[i - 1][4]。
简单来说,一维情况正序更新状态f[j]需要用到前面计算的状态已经被「污染」,逆序则不会有这样的问题。
状态转移方程为:f[j] = max(f[j], f[j - v[i]] + w[i] 。
tips:若通过减少维数来进行状态压缩,要注意是否有一维循环需要逆序来保证更新所用到的状态没有被污染。
对应代码
#include<iostream>
#include<cstdio>
#include<cstring>using namespace std;const int N = 1010;int v[N], w[N];
int f[N];int n, m;int main(){scanf("%d%d", &n, &m);for(int i = 1; i <= n; ++ i) scanf("%d%d", &v[i], &w[i]);for(int i = 1; i <= n; ++ i){for(int j = m; j >= v[i]; -- j){f[j] = max(f[j], f[j-v[i]]+w[i]);}}printf("%d", f[m]);return 0;
}二、完全背包
(一)题目
有 N 种物品和一个容量是V的背包,每种物品都有无限件可用。
第i种物品的体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式
第一行两个整数,N,V,用空格隔开,分别表示物品种数和背包容积。
接下来有N行,每行两个整数 vi,wi,用空格隔开,分别表示第i种物品的体积和价值。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N,V≤1000
0<vi,wi≤1000
输入样例
4 5
1 2
2 4
3 4
4 5
输出样例:
10
(二)题解
闫式DP分析法
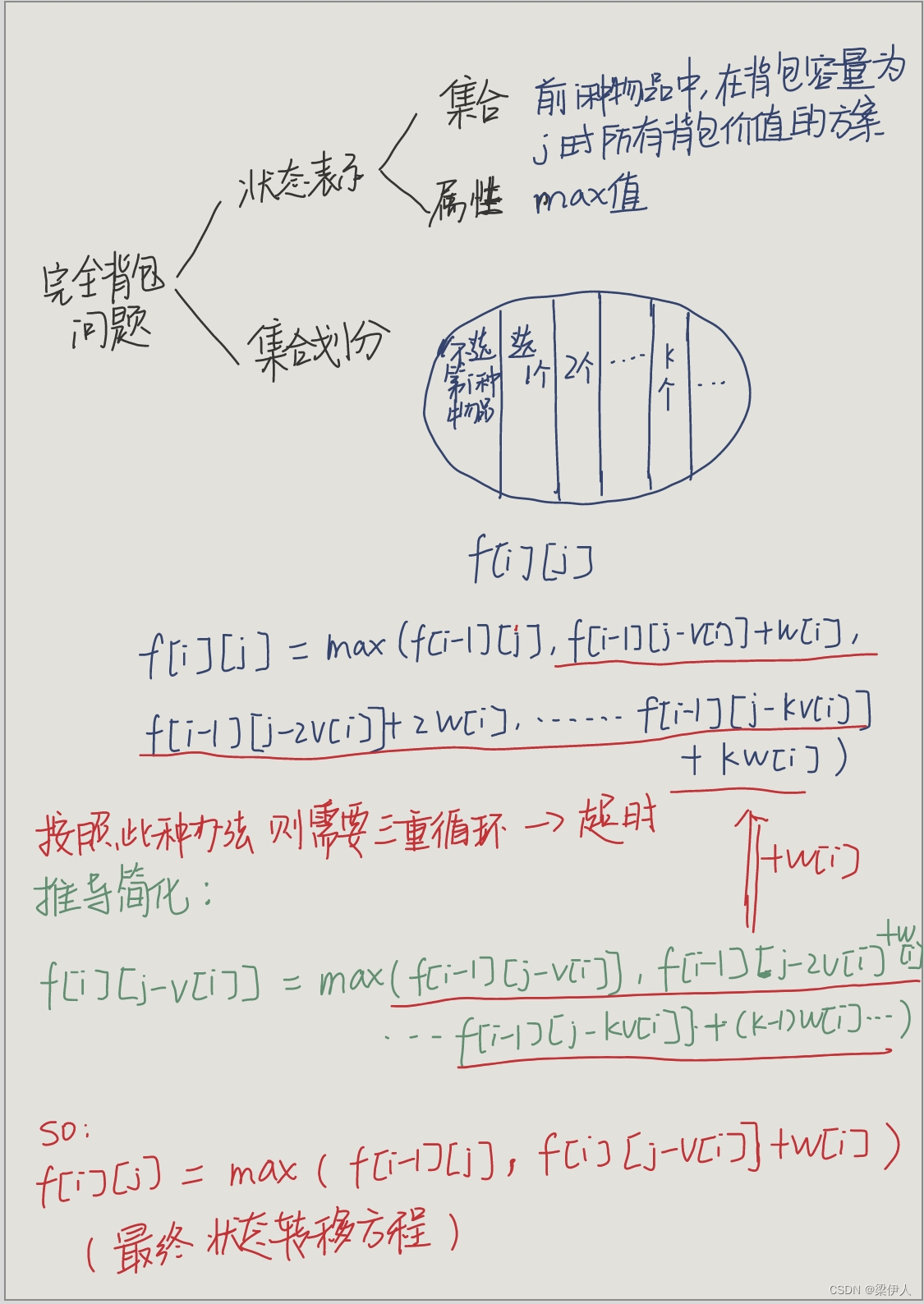
对应代码
二维DP
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>using namespace std;const int N = 1010;int v[N], w[N];
int f[N][N];int n, m;int main(){scanf("%d%d", &n, &m);for(int i = 1; i <= n; ++ i) scanf("%d%d", &v[i], &w[i]);for(int i = 1; i <= n; ++ i){for(int j = 0; j <= m; ++ j){f[i][j] = f[i-1][j];if(j >= v[i]) f[i][j] = max(f[i][j], f[i][j-v[i]]+w[i]); }}printf("%d", f[n][m]);return 0;
}一维DP
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>using namespace std;const int N = 1010;int v[N], w[N];
int f[N];int n, m;int main(){scanf("%d%d", &n, &m);for(int i = 1; i <= n; ++ i) scanf("%d%d", &v[i], &w[i]);for(int i = 1; i <= n; ++ i){for(int j = 0; j <= m; ++ j){f[j] = f[j]; // 等价替换f[i][j] = f[i-1][j];if(j >= v[i]) f[j] = max(f[j], f[j-v[i]]+w[i]); // 等价替换f[i][j] = max(f[i][j], f[i][j-v[i]]+w[i])// 总结:替换的是f[i-1][...]还是f[i][...]取决于在该i层循环中,等号右边的数组中出现的下标有没有更新过,若更新过就是f[i][...], 反之则是f[i-1][...]}}printf("%d", f[m]);return 0;
}简化
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>using namespace std;const int N = 1010;int v[N], w[N];
int f[N];int n, m;int main(){scanf("%d%d", &n, &m);for(int i = 1; i <= n; ++ i) scanf("%d%d", &v[i], &w[i]);for(int i = 1; i <= n; ++ i){for(int j = v[i]; j <= m; ++ j){f[j] = max(f[j], f[j-v[i]]+w[i]); }}printf("%d", f[m]);return 0;
}三、多重背包问题
(一)题目
有N 种物品和一个容量是V的背包。
第i种物品最多有 si 件,每件体积是vi,价值是wi。
求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大。
输出最大价值。
输入格式
第一行两个整数,N,V,用空格隔开,分别表示物品种数和背包容积。
接下来有N行,每行三个整数 vi,wi,si,用空格隔开,分别表示第i种物品的体积、价值和数量。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N≤1000
0<V≤2000
0<vi,wi,si≤2000
输入样例
4 5
1 2 3
2 4 1
3 4 3
4 5 2
输出样例
10
(二)题解
思路:可以将多重背包问题转化为01背包问题。
1.朴素的转化思路
可以直接转化为有s[1]+s[2]+...s[n]个物品,背包容量为V的01背包问题。
对应代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>using namespace std;const int N = 110;int n, m;int f[N];int main(){scanf("%d%d", &n, &m);for(int i = 1; i <= n; ++ i){int v, w, s;scanf("%d%d%d", &v, &w, &s);for(int j = m; j >= 0; -- j){for(int k = 1; k <= s; ++ k){if(j >= k*v) f[j] = max(f[j], f[j-k*v]+k*w);}}}printf("%d", f[m]);return 0;
}时间复杂度分析
O(N*V*Si)(大约为10^9)在本题目的数据范围限制下会超时。
2.优化
上述做法是将Si拆成了Si个1。
tips:
能否将Si拆成小于Si个数,使这些数可以表示1~Si之间的所有数?
答案是可以的。
(结论)其实只需要将Si拆成log(Si)(上取整)个数即可。这Si个数分别为2^0, 2^1, 2^2……2^log(Si)。
注意:对于Si恰好等于以2为底的指数减1倍时,是恰好符合题意的。而其他值在经过log(Si)(上取整)个数相加后仍会小于Si,只需要将剩余的这部分单独拿出来即可。
对应代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>using namespace std;const int N = 2010;int n, m;int f[N];struct good{int v, w;
};int main(){vector<good> goods;scanf("%d%d", &n, &m);for(int i = 0; i < n; ++ i){int v, w, s;scanf("%d%d%d", &v, &w, &s);for(int k = 1; k <= s; k *= 2){s -= k;goods.push_back({k*v, k*w});}if(s > 0) goods.push_back({s*v, s*w});}for(auto item: goods){for(int j = m; j >= item.v; -- j){f[j] = max(f[j], f[j-item.v]+item.w);}}printf("%d", f[m]);return 0;
}四、分组背包问题
(一)题目
有 N 组物品和一个容量是V的背包。
每组物品有若干个,同一组内的物品最多只能选一个。
每件物品的体积是 vij,价值是 wij,其中 i 是组号,j是组内编号。
求解将哪些物品装入背包,可使物品总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式
第一行有两个整数 N,V,用空格隔开,分别表示物品组数和背包容量。
接下来有N组数据:
- 每组数据第一行有一个整数 S,表示第i个物品组的物品数量;
- 每组数据接下来有 S行,每行有两个整数 vij,wij,用空格隔开,分别表示第 i 个物品组的第j个物品的体积和价值;
输出格式
输出一个整数,表示最大价值。
数据范围
0<N,V≤100
0<Si≤100
0<vij,wij≤100
输入样例
3 5
2
1 2
2 4
1
3 4
1
4 5
输出样例
8
(二)题解
注意:多重背包问题是分组背包问题的一个特殊情况。
分组背包问题同样也是01背包问题的一个变种。
对应代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>using namespace std;const int N = 110;int n, m;int v[N], w[N];
int f[N];int main(){scanf("%d%d", &n, &m);for(int i = 0; i < n; ++ i){int s;scanf("%d", &s);for(int j = 1; j <= s; ++ j) scanf("%d%d", &v[j], &w[j]);for(int j = m; j >= 0; -- j){for(int k = 1; k <= s; ++ k){if(j >= v[k]) f[j] = max(f[j], f[j-v[k]]+w[k]);}}}printf("%d", f[m]);return 0;
}总结
01背包问题,多重背包问题,分组背包问题是同一大类背包问题。在i层循环中只能做一个选择(即选与不选)(对于多重背包和分组背包的选对应的是多种选择)。
而完全背包是另一大类问题。
相关文章:

算法学习之动态规划DP——背包问题
一、01背包问题 (一)题目 有 N 件物品和一个容量是 V的背包。每件物品只能使用一次。 第i件物品的体积是 vi,价值是 wi。 求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。 输出最大价值…...
LeetCode刷题日志-17.电话号码的字母组合
纯暴力解法,digits有多长,就循环多少次进行字母组合 class Solution {public List<String> letterCombinations(String digits) {List<String> reslut new ArrayList<>();if(digits.equals(""))return reslut;Map<Inte…...

选修-单片机作业第1/2次
第一次作业 第二次作业 1、51 系列单片机片内由哪几个部分组成?各个部件的最主要功能是什么? 51系列单片机的内部主要由以下几个部分组成,每个部件的主要功能如下: 1. **中央处理器(CPU)**:这是…...

微信小程序开发系列(十七)·事件传参·mark-自定义数据
目录 步骤一:按钮的创建 步骤二:按钮属性配置 步骤三:添加点击事件 步骤四:参数传递 步骤五:打印数据 步骤六:获取数据 步骤七:父进程验证 总结:data-*自定义数据和mark-自定…...
企业战略管理 找准定位 方向 使命 边界 要干什么事 要做多大的生意 资源配置投入
AI突破千行百业,也难打破护城河 作为每个企业或个人的立命生存之本,有的企业在某个领域长期努力筑起了高高的护城河。 战略是什么?用处,具体内容 企业战略是指企业为了实现长期目标,制定的总体规划和长远发展方向。…...
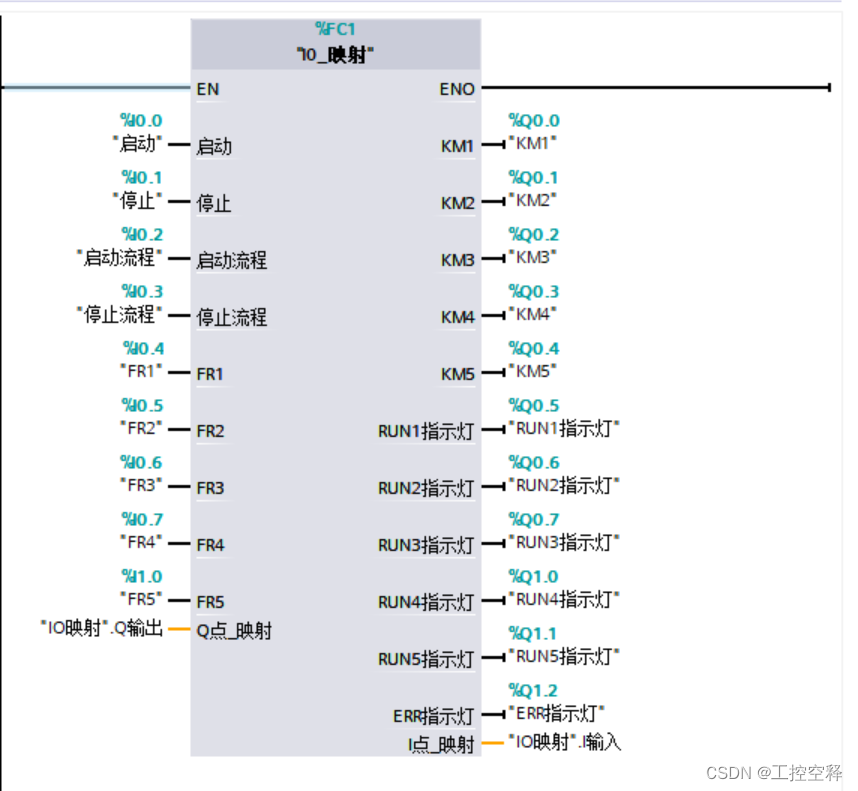
记录西门子:IO隔离SCL编程
在PLC变量中创建IO输入输出 在PLC类型中创建输入和输出,并将PLC变量的输入输出名称复制过来 创建一个FC块或者FB块 创建一个DB块 MAIN主程序中:...
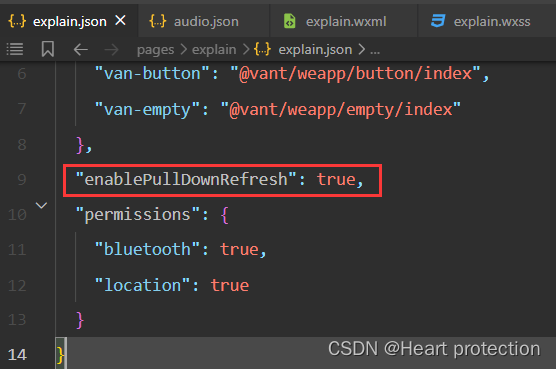
微信小程序如何实现下拉刷新
1.首先在你需要实现下拉刷新页面的json文件中写入"enablePullDownRefresh": true。 2.在js文件的onPullDownRefresh() 事件中实现下拉刷新。 实现代码 onPullDownRefresh() {console.log(开始下拉刷新)wx.showNavigationBarLoading()//在标题栏中显示加载图标this.d…...
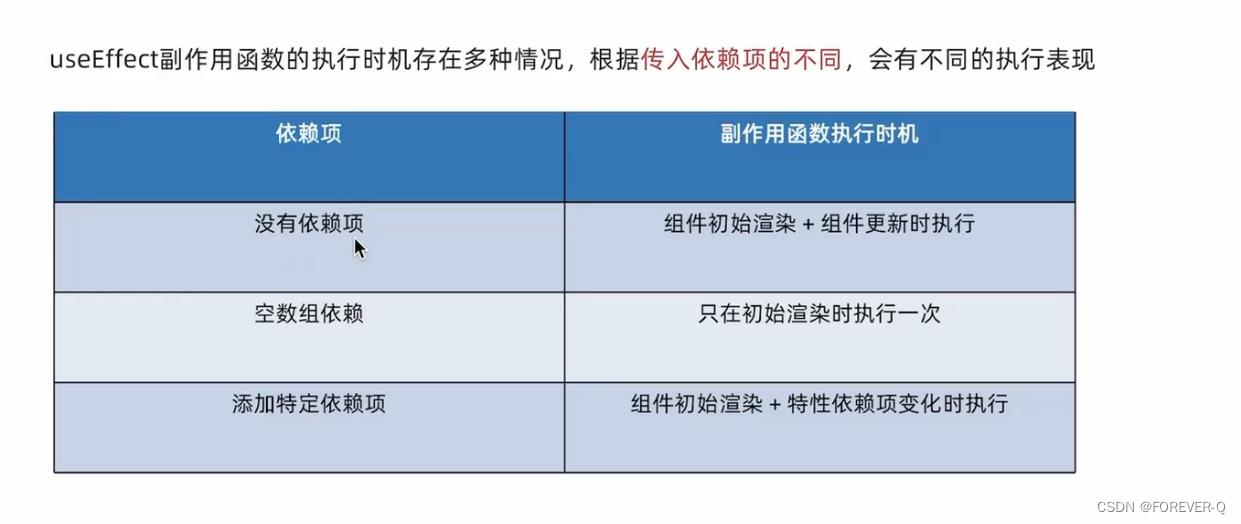
React-useEffect
1.概念 说明:用于在React组件中创建不是由事件引起而是由渲染本身引起的操作,比如发送 A列AX请求,更改DOM等。 2.案例 // useEffect用于组件不是由事件引起的而是由渲染本身引起的操作,如ajax,更改Dom等。 import { useEffect,…...

web蓝桥杯真题:展开你的扇子
代码: /*TODO:请补充 CSS 代码*/#box:hover #item7 {transform: rotate(10deg); } #box:hover #item6 {transform: rotate(-10deg); } #box:hover #item8 {transform: rotate(20deg); } #box:hover #item5 {transform: rotate(-20deg); } #box:hover #i…...

阿里P9大佬分享:如何让代码更加灵活
面试官: 你好,今天我们要讨论的是命令模式。首先,你能解释一下什么是命令模式吗? 求职者: 当然可以。命令模式是一种行为设计模式,它将一个请求封装成一个对象,从而让你使用不同的请求、队列或者日志请求来参数化其他…...

SpringBoot中加载配置文件的优先级
在Spring Boot中,加载配置文件的优先级按照以下顺序进行,后续的配置会覆盖之前的配置: 默认属性:这些属性在Spring Boot本身中定义,并且通常是不可变的。它们作为后备值。 应用程序属性:这些属性在应用程序…...

Mysql命令行客户端
命令行客户端 操作数据库操作数据表 操作数据库 mysql> create database mike charsetutf8; Query OK, 1 row affected (0.01 sec) mysql> show databases; -------------------- | Database | -------------------- | information_schema | | mike …...

开源的python 游戏开发库介绍
本文将为您详细讲解开源的 Python 游戏开发库,以及它们的特点、区别和应用场景。Python 社区提供了多种游戏开发库,这些库可以帮助您在 Python 应用程序中实现游戏逻辑、图形渲染、声音处理等功能。 1. Pygame 特点 - 基于 Python 的游戏开发库。…...

批量提取PDF指定区域内容到 Excel 以及根据PDF里面第一页的标题来批量重命名-附思路和代码实现
首先说明下,PDF需要是电子版本的,不能是图片或者无法选中的那种。 需求1:假如我有一批数量比较多的同样格式的PDF电子文档,需要把特定多个区域的数字或者文字提取出来 需求2:我有一批PDF文档,但是文件的名…...
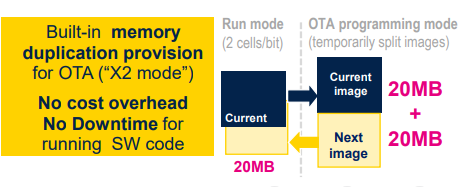
PCM会重塑汽车OTA格局吗(1)
目录 1.汽车OTA概述 2.ST如何考虑OTA? 2.1 Stellar四大亮点 2.2 PCM技术视角下的OTA 3.小结 1.汽车OTA概述 随着智能网联汽车的飞速发展,汽车OTA也越来越盛行; 目前来讲OTA分为FOTA和SOTA(Software-over-the-air)两种,区别…...
Intel® Extension for PyTorch*详细安装教程
最近在研究Intel的pytorch的加速拓展Intel Extension for PyTorch*,但是发现官网的文档全是英文的,不太好找安装教程。所以特此分享Intel Extension for PyTorch*的详细安装教程。 文章目录 一、安装所需系统要求1.1 硬件需求1.2 软件需求 二、准备2.1 安装驱动程序…...
云上攻防-云产品篇堡垒机场景JumpServer绿盟SASTeleport麒麟齐治
知识点 1、云产品-堡垒机-产品介绍&攻击事件 2、云产品-堡垒机-安全漏洞&影响产品 章节点: 云场景攻防:公有云,私有云,混合云,虚拟化集群,云桌面等 云厂商攻防:阿里云,腾讯…...
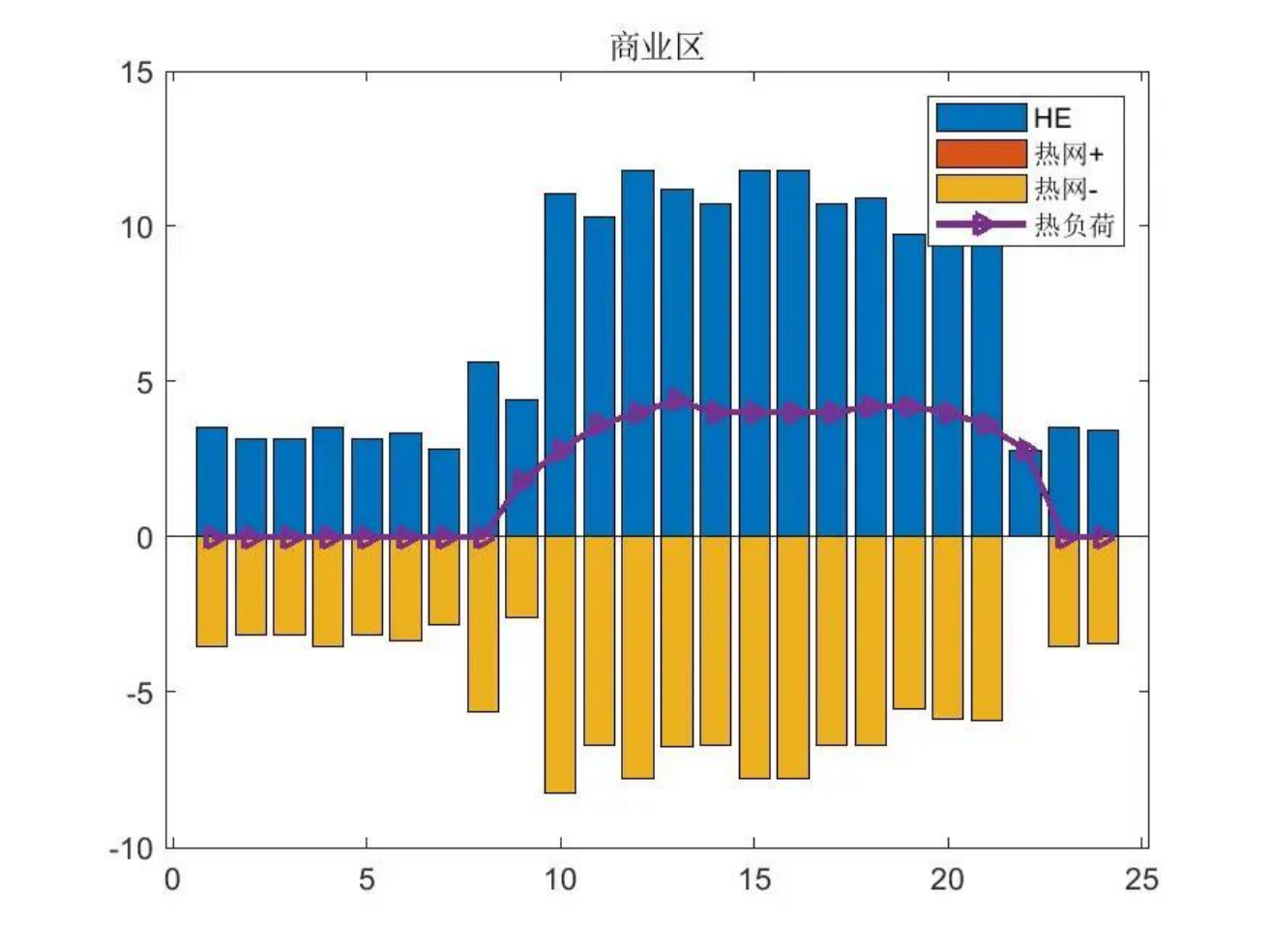
【顶刊|修正】多区域综合能源系统热网建模及系统运行优化【复现+延伸】
目录 主要内容 部分代码 结果一览 下载链接 主要内容 该程序复现《多区域综合能源系统热网建模及系统运行优化》模型并进一步延伸,基于传热学的基本原理建立了区域热网能量传输通用模型,对热网热损方程线性化实现热网能量流建模࿰…...

使用Numpy手工模拟梯度下降算法
代码 import numpy as np # Compute every step manually# Linear regression # f w * x # here : f 2 * x X np.array([1, 2, 3, 4], dtypenp.float32) Y np.array([2, 4, 6, 8], dtypenp.float32)w 0.0# model output def forward(x):return w * x# loss MSE def loss…...
金融数据采集与风险管理:Open-Spider工具的应用与实践
一、项目介绍 在当今快速发展的金融行业中,新的金融产品和服务层出不穷,为银行业务带来了巨大的机遇和挑战。为了帮助银行员工更好地应对这些挑战,我们曾成功实施了一个创新的项目,该项目采用了先进的爬虫技术,通过ope…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...
