【论文阅读随笔】RoPE/旋转编码:ROFORMER: ENHANCED TRANSFORMER WITH ROTARY POSITION EMBEDDING
文章目录
- 1.目的:通过绝对位置编码的方式实现相对位置编码
- 2.理解RoPE,在我看来有几个需要注意的点:
- 3.本文相关复数概念:
- 3.1.复数乘法的几何意义
- 3.2.复数内积 VS. 复数乘法
- 4.REF:
1.目的:通过绝对位置编码的方式实现相对位置编码
- 绝对位置编码比较简单,加或乘一个有次序的数
- 实现相对位置编码,也即意味着,要蕴含位置差的信息:
- 假设m是某个token的位置信息,n是另一个token的位置信息,要有类似 m − n m-n m−n的信息,比较容易想到复数乘法会产生 m − n m-n m−n,以及复数乘法和复数内积的性质。
2.理解RoPE,在我看来有几个需要注意的点:
- 最重要的是 e i m θ e^{im\theta} eimθ 的构造,给二维的 q ⃗ \vec q q或 k ⃗ \vec k k乘这个量(也即对 q ⃗ \vec q q或 k ⃗ \vec k k做了旋转),旋转后再对二者进行内积便会产生 m − n m-n m−n的相对位置信息,也就达成了相对位置编码的目的
- 二维向量和复数平面存在一一对应的关系
- 二维扩展到 2 ∗ N 2*N 2∗N维:既然二维的向量旋转后,再做内积有 m − n m-n m−n的相对位置信息,那就直接把 q ⃗ \vec q q和 k ⃗ \vec k k都分成2维一组,这样 q ⃗ \vec q q和 k ⃗ \vec k k做内积时,就让分好的组与组之间做内积,就自然让各位置携带相对位置信息了
- 向量旋转有两种计算方式,一种是复数乘取实部,另一种是通过构造旋转矩阵计算
3.本文相关复数概念:
3.1.复数乘法的几何意义
- 两个复数相乘,得到的复数的模长是原来两个复数的模长的乘积,得到的复数的幅角是原来两个复数的幅角的相加。
3.2.复数内积 VS. 复数乘法
- 复数内积: ⟨ ( a + b i ) , ( c + d i ) ⟩ = a c + b d {\left \langle (a+bi),(c+di)\right \rangle }=ac+bd ⟨(a+bi),(c+di)⟩=ac+bd(不含i)
- 复数乘法: ( a + b i ) ( c + d i ) = ( a c − b d ) + ( b c − a d ) i (a+bi)(c+di)=(ac-bd) + (bc-ad)i (a+bi)(c+di)=(ac−bd)+(bc−ad)i
- 复数内积的结果跟复数乘法的实部相差了一个正负号,复数内积等于复数乘以另一个复数的共轭后取实部:
- ⟨ ( a + b i ) , ( c + d i ) ⟩ = R E [ ( a + b i ) ( c + d i ) ∗ ] {\left \langle (a+bi),(c+di)\right \rangle }=RE[(a+bi)(c+di)^*] ⟨(a+bi),(c+di)⟩=RE[(a+bi)(c+di)∗]
- 也即: ⟨ ( a + b i ) , ( c + d i ) ⟩ = R E [ ( a + b i ) ( c − d i ) ] {\left \langle (a+bi),(c+di)\right \rangle }=RE[(a+bi)(c-di)] ⟨(a+bi),(c+di)⟩=RE[(a+bi)(c−di)]
4.REF:
[1].https://zhuanlan.zhihu.com/p/642884818 (这篇讲的很清楚了)
[2].https://zhuanlan.zhihu.com/p/669797102
[3].https://zhuanlan.zhihu.com/p/647109286
[4].https://kexue.fm/archives/8265
[5].https://zhuanlan.zhihu.com/p/641865355
[6].https://zhuanlan.zhihu.com/p/646598747
[7].学习报告:向量与复数的联系
[8].复向量的内积,想不明白?
[9].https://arxiv.org/pdf/2104.09864.pdf
相关文章:

【论文阅读随笔】RoPE/旋转编码:ROFORMER: ENHANCED TRANSFORMER WITH ROTARY POSITION EMBEDDING
文章目录 1.目的:通过绝对位置编码的方式实现相对位置编码2.理解RoPE,在我看来有几个需要注意的点:3.本文相关复数概念:3.1.复数乘法的几何意义3.2.复数内积 VS. 复数乘法 4.REF: 1.目的:通过绝对位置编码的…...

数据挖掘
一.数据仓库概述: 1.1数据仓库概述 1.1.1数据仓库定义 数据仓库是一个用于支持管理决策的、面向主题、集成、相对稳定且反映历史变化的数据集合。 1.1.2数据仓库四大特征 集成性(Integration): 数据仓库集成了来自多个不同来源…...
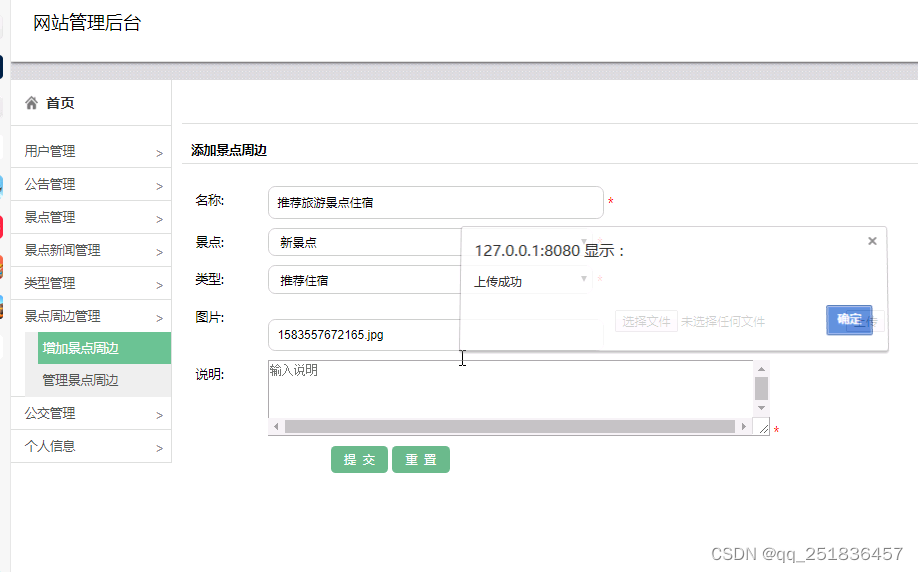
java SSM旅游景点与公交线路查询系统myeclipse开发mysql数据库springMVC模式java编程计算机网页设计
一、源码特点 java SSM旅游景点与公交线路查询系统是一套完善的web设计系统(系统采用SSM框架进行设计开发,springspringMVCmybatis),对理解JSP java编程开发语言有帮助,系统具有完整的源代码和数据库,系…...

解决Git报错:fatal: detected dubious ownership in repository at
在通过 Git Bash 提交项目代码时输入 git add . 命令后,报错:fatal: detected dubious ownership in repository at 这是因为该项目的所有者与现在的用户不一致 比如说: 该项目的所有者是 Administrator,而当前用户是 YuYang, 那…...
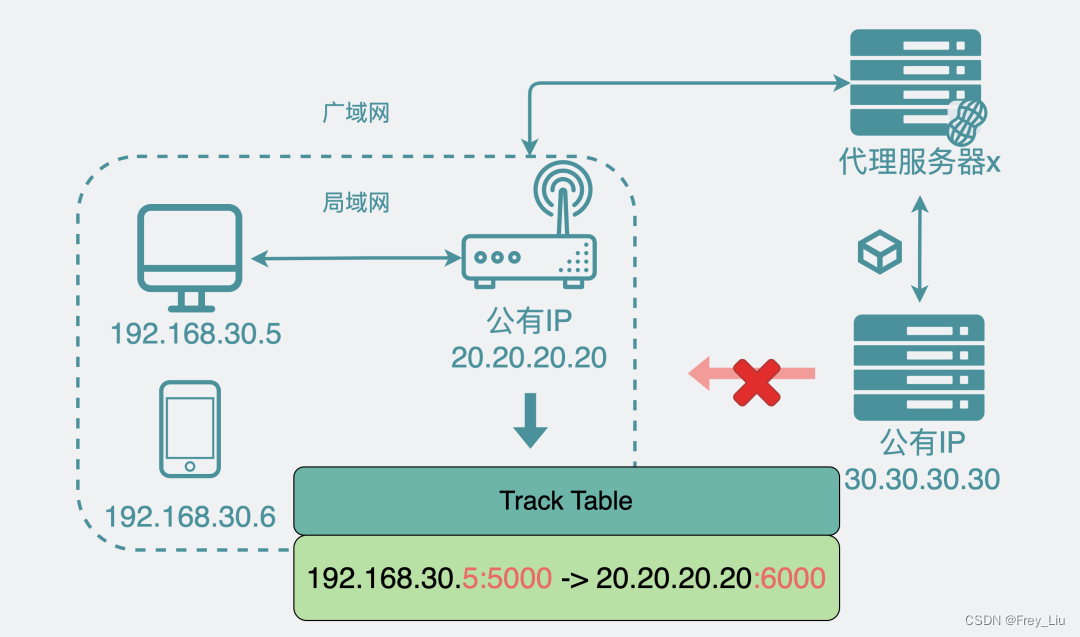
网络协议常见问题
网络协议常见问题 OSI(Open Systems Interconnection)模型OSI 封装 TCP/IP协议栈IP数据报的报头TCP头格式UDP头格式TCP (3-way shake)三次握手建立连接:为什么三次握手才可以初始化 Socket、序列号和窗口大小并建立 TCP 连接。每次建立TCP连接…...

人工智能的迷惑行为
目录 前言1 人工智能的“幽默”瞬间1.1 语义误解1.2 逻辑错误 2 技术原理探究2.1 算法设计缺陷2.2 数据处理不当 3 社会影响分析3.1 信任度下降3.2 技术担忧 结语 前言 随着人工智能技术的迅猛发展,各类AI大模型如ChatGPT、文心一言、通义千问等纷纷登场࿰…...

XR技术:短剧制作的全新纪元
在数字技术的浪潮中,XR(扩展现实)技术以其独特的魅力,正在为短剧制作带来革命性的突破。这种融合了虚拟现实、增强现实和混合现实等先进技术的创新工具,正逐渐改变着短剧制作的传统模式,引领着短剧艺术走向…...
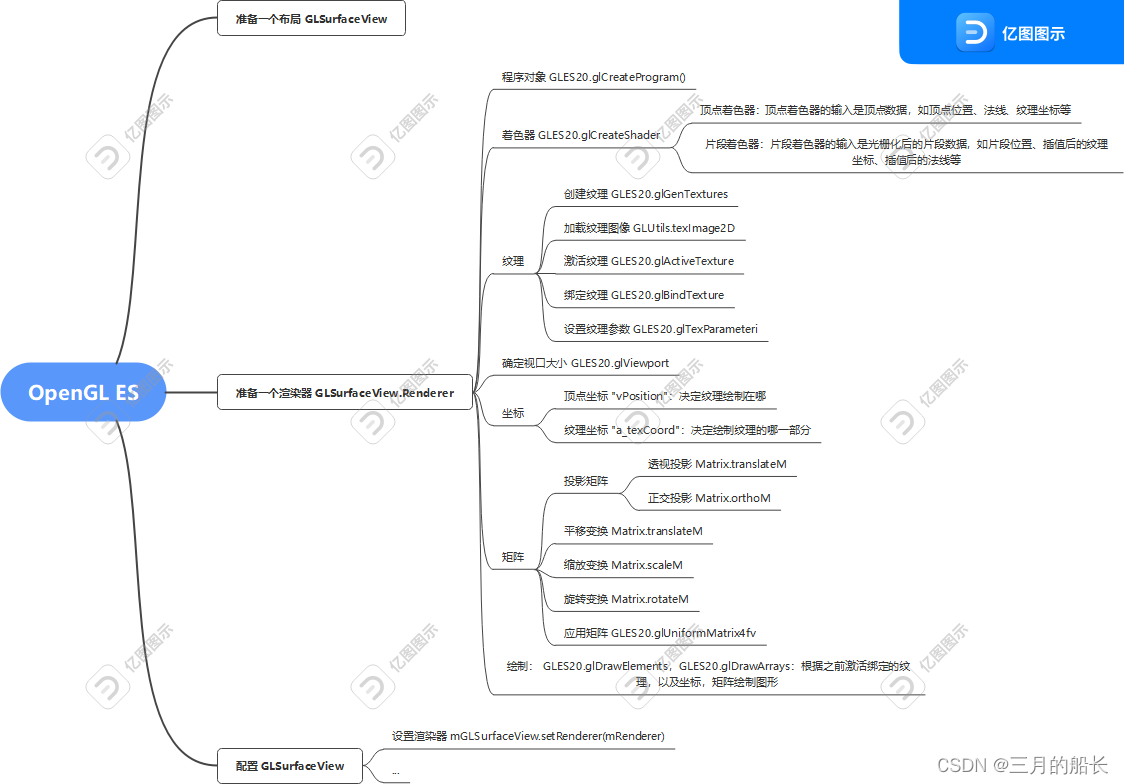
安卓 OpenGL ES 学习笔记
文章目录 OpenGL 学习笔记OpenGL 是什么?OpenGL ES是什么?怎么用?hello world如何实现动画效果 参考文章 OpenGL 学习笔记 OpenGL 是什么? OpenGL(Open Graphics Library)是一个跨平台的图形编程接口&…...

git分布式管理-头歌实验冲突处理、忽略文件
一、解决冲突 任务描述 在团队协作开发过程中,可能你和团队中的其他成员,都修改了某个文件的某一部分内容,且其他成员已将该修改推送到了远程仓库。这样当你需要合并他的代码的时候,可能就会在内容上出现冲突,这个时候…...

【实战项目】网络编程:在Linux环境下基于opencv和socket的人脸识别系统--C++实现
🌞前言 这里我们会实现一个项目:在linux操作系统下基于OpenCV和Socket的人脸识别系统。 目录 🌞前言 🌞一、项目介绍 🌞二、项目分工 🌞三、项目难题 🌞四、实现细节 🌼4.1 关…...

零售EDI:劳氏 Lowe‘s EDI项目案例
通过 EDI,企业与Lowes之间可以直接交换各种商业文档,如订单、发票、收据等,从而实现信息的实时交换,提高了供应链的效率和准确性。在现代供应链管理中,EDI 已经成为了不可或缺的重要工具。 作为一家拥有多条业务线的企…...
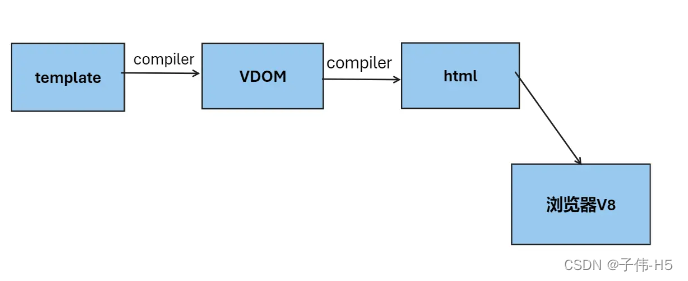
为什么不用 index 做 key?
“在 Vue 中,我们在使用 v-for 渲染列表的时候,为什么要绑定一个 key?能不能用 index 做 key?” 在聊这个问题之前我们还得需要知道 Vue 是如何操作 DOM 结构的。 虚拟DOM 我们知道,Vue 不可以直接操作 DOM 结构&am…...
Linux虚拟机安装Redis
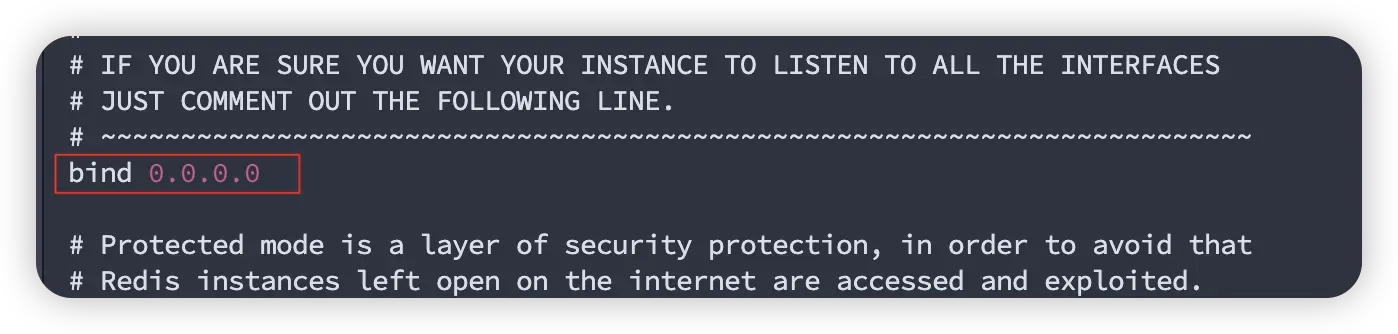
官网下载压缩包:官网链接,然后将对应的tar.gz压缩包放入虚拟机下的/opt目录下。由于redis是C语言开发的,因此需要安装gcc编译器来编译代码,我们下载的压缩包里面是源代码,需要编译。通过yum install gcc指令下载C语言的…...

网络安全: Kali Linux 进行 SSH 渗透与防御
目录 一、实验 1.环境 2.nmap扫描目标主机 3.Kali Linux 进行 SSH 渗透 3.Kali Linux 进行 SSH 防御 二、问题 1.SSH有哪些安全配置 一、实验 1.环境 (1)主机 表1 主机 系统版本IP备注Kali Linux2022.4 192.168.204.154(动态&…...

近年来文本检测相关工作梳理
引言 场景文本检测任务,一直以来是OCR整个任务中最为重要的一环。虽然有一些相关工作是端对端OCR工作的,但是从工业界来看,相关落地应用较为困难。因此,两阶段的OCR方案一直是优先考虑的。 在两阶段中(文本检测文本识…...

文件系统事件监听
文件系统事件和网络IO事件一样,也可以通过epoll或者IOCP 事件管理器统一调度,当所监控的文件或文件夹发生了增删改的事件时,就会触发事件回调,进行事件处理。很常见的应用,如配置文件立即生效功能,就可以通…...

探秘HTTPS:如何通过SSL/TLS保证网络通信安全
目录 引言 详解HTTPS加密实现机制 SSL/TLS工作原理 结论 引言 随着网络安全威胁的日益增加,HTTPS通过SSL(Secure Sockets Layer)和TLS(Transport Layer Security)协议提供的加密技术变得至关重要。这些技术保证了用…...

Java算法之动态规划
Java算法之动态规划 前言 最近这一段时间一直在刷算法题,基本上一有时间就会做一两道,这两天做了几道动态规划的问题,动态规划之前一直是我比较头疼的一个问题,感觉好复杂,一遇到这样的问题就想跳过,昨…...
)
C++从零开始的打怪升级之路(day47)
这是关于一个普通双非本科大一学生的C的学习记录贴 在此前,我学了一点点C语言还有简单的数据结构,如果有小伙伴想和我一起学习的,可以私信我交流分享学习资料 那么开启正题 今天分享的是关于set和map的知识点 1.关联式容器 在前面&#…...

香橙派AIpro开发板开箱测评
2023年12月,香橙派联合华为发布了基于昇腾的Orange Pi AIpro开发板,提供8/20TOPS澎湃算力,能覆盖生态开发板者的主流应用场景,让用户实践各种创新场景,并为其提供配套的软硬件。香橙派AIpro开发板一经发布便吸引了众多…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...

stm32wle5 lpuart DMA数据不接收
配置波特率9600时,需要使用外部低速晶振...

深入浅出WebGL:在浏览器中解锁3D世界的魔法钥匙
WebGL:在浏览器中解锁3D世界的魔法钥匙 引言:网页的边界正在消失 在数字化浪潮的推动下,网页早已不再是静态信息的展示窗口。如今,我们可以在浏览器中体验逼真的3D游戏、交互式数据可视化、虚拟实验室,甚至沉浸式的V…...

如何通过git命令查看项目连接的仓库地址?
要通过 Git 命令查看项目连接的仓库地址,您可以使用以下几种方法: 1. 查看所有远程仓库地址 使用 git remote -v 命令,它会显示项目中配置的所有远程仓库及其对应的 URL: git remote -v输出示例: origin https://…...

CppCon 2015 学习:REFLECTION TECHNIQUES IN C++
关于 Reflection(反射) 这个概念,总结一下: Reflection(反射)是什么? 反射是对类型的自我检查能力(Introspection) 可以查看类的成员变量、成员函数等信息。反射允许枚…...
