Java算法之动态规划
Java算法之动态规划
前言
最近这一段时间一直在刷算法题,基本上一有时间就会做一两道,这两天做了几道动态规划的问题,动态规划之前一直是我比较头疼的一个问题,感觉好复杂,一遇到这样的问题就想跳过,昨天耐着性子做了一道动态规划的题,感觉没有我想象的那么难,无非就是先定义dp数组,然后找到初始值,再写出状态转移方程,一步一步来,难点就是如何确定一个正确的状态,这是一个一直困扰我的问题,而且在写状态方程时要细心一点,不要出现错误,这篇文章就是记录一下自己的学习体会和心得。
动态规划的基本概念
动态规划(Dynamic Programming,简称DP)是一种在数学、计算机科学和经济学中使用的,通过把原问题分解为相对简单的子问题的方式来求解复杂问题的方法。动态规划常常适用于有重叠子问题和最优子结构特性的问题。
动态规划的基本思想是,将待求解的问题分解成若干个相互联系的子问题,先求解子问题,然后从这些子问题的解得到原问题的解。动态规划的关键在于正确地定义子问题,以及子问题的解如何推导出原问题的解。
动态规划通常用于求解具有最优子结构特性的问题,即问题的最优解可以由其子问题的最优解有效地构造出来。此外,动态规划还要求子问题空间必须足够小,即子问题的数量随着问题规模的增加不会增长得太快,以便能够用有限的内存和时间来解决。
贪心算法
在这里我想提一下贪心算法,为什么要提一下贪心算法呢,因为我觉得这两个算法之间存在一些共同点。贪心算法(Greedy Algorithm)是一种在每一步选择中都采取在当前状态下最好或最优(即最有利)的选择,从而希望导致结果是全局最好或最优的算法。这和动态规划的将问题分解为若干个子问题求解有些类似,都是从每一个小问题出发,然后慢慢扩展到最后的原问题,这两个算法在最优子结构特性的问题解决上都尤为有效,贪心算法的优点是简单、直观且运行速度快,因为每一步只关注当前状态下的最优选择,而不考虑未来可能的变化。但是,如果问题不满足贪心选择性质,贪心算法就无法保证得到全局最优解。在这种情况下,可能需要使用其他方法,如动态规划。
先举一个贪心算法的小例子,比如找零问题就是一个典型的贪心算法应用。假设有面值为1元、2元、5元、10元、20元、50元、100元的纸币,目标是找出一个给定金额的最少纸币数。贪心策略是每次尽可能选择面值最大的纸币,因为这样可以减少纸币的数量。
再举一个不满足贪心选择的性质,比如贪心算法的一个经典案例,背包问题,背包问题有一个背包,背包容量是M=150。有7个物品,物品可以分割成任意大小。要求尽可能让装入背包中的物品总价值最大,但不能超过总容量。那么运用贪心算法的思想,先求出每种物品的单位价值,再从最值钱的开始装,直到背包装满为止。但如果对这道题修改一下,不能分割物品,那此时贪心算法就会失效,这就是0-1背包问题。此时,需要用动态规划来解决。
几道例题
1.0-1背包问题

public class Main {public static void main(String[] args) {Scanner scan = new Scanner(System.in);//输入商场物品的数量int N = scan.nextInt();//输入小明的背包容量int V = scan.nextInt();//定义两个数组分别记录商品的重量和价格int[] weight = new int[N];int[] value = new int[N];for (int i = 0; i < N; i++) {//重量weight[i] = scan.nextInt();//价值value[i] = scan.nextInt();}//设置dp表int[][] dp = new int[N+1][V+1];//循环遍历每一个商品,每次循环都要得出在背包容量为1-->V的每种情况下,他所含的价值for (int j = 1;j<=N;j++){//从背包容量为1时开始遍历for(int k = 1;k<=V;k++){//如果商品容量大于背包容量,那么就装不进去,那么总价值就为前一个商品在这个容量的总价值if(weight[j-1]>k){dp[j][k] = dp[j-1][k];}//否则,比较放入当前物品和不放入当前物品哪种情况价值更高else{//dp[j-1][k-weight[j-1]]这个代码是为了求减去当前商品的容量后,背包的总价值,再加上此时加入这个商品后的价值,得到一个新的总价值,如果这个总价值大于相同容量下前一个商品的价值,那么就值得放入,否则不值得放入dp[j][k] = Math.max(dp[j-1][k-weight[j-1]]+value[j-1],dp[j-1][k]);}}}System.out.println(dp[N][V]);scan.close();}
}
2.爬楼梯
题目描述:假设你现在正在爬楼梯。需要n阶你才能到达楼顶。每次你可以爬1或者2个台阶,一共有多少种方法可以到达楼顶?
那么对于这题,很明显我们可以使用动态规划来进行求解,状态很好确定,首先确立边界,当爬一层有多少方法,当爬两层有多少种方法,那么设立状态转移方程,当爬第n阶时,有两种状态,要么现在处于第n-1个阶梯,要么现在处于第n-2个阶梯,那爬第n阶的方法总数就是爬n-1个阶梯的方法数加上爬n-2个阶梯的方法数。
class Solution {public int climbStairs(int n) {//当n为1时直接返回1,这里返回是因为后面dp数组长度为n+1,如果n为1,那后面对dp[2]赋值就会出现溢出if(n == 1){return 1;} //设置dp数组,表示爬第n阶台阶的方法数 int [] dp = new int[n+1];//爬第1阶台阶的方法数dp[1] = 1;//爬第2阶台阶的方法数dp[2] = 2;//从第三阶开始循环遍历for(int i = 3;i < n+1;i++){//状态转移方程dp[i] = dp[i-2] + dp[i-1];}//返回return dp[n];}}
3.买股票的最佳时机

在练习数组的相关算法题时,有过一道买卖股票的题,但这两个题不太一样,但都是用动态规划来解决的,这道题要求是只能买卖一次,那根据动态规划的思想,每天都有两种状态,一种是手里没有股票,一种是手里有股票,那可以设置两个边界,一个是第一天手里没有股票的利润,一种是手里有股票的利润,然后递推下一个,根据题目我们知道只能买卖一次,那么如果这一天手里有股票,那可能是前面买的,也可能是今天买的,有这两种情况,比较两种的较大者作为当天有股票的最大利润。
如果当天手里没有股票,那可能是前面卖的,也可能是当天卖的,同样,我们比较两者的较大值作为当天的最大利润。
class Solution {public int maxProfit(int[] prices) {if (prices == null || prices.length == 0)return 0;int length = prices.length;int[][] dp = new int[length][2];//边界条件dp[0][0]= 0;dp[0][1] = -prices[0];for (int i = 1; i < length; i++) {//递推公式dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);dp[i][1] = Math.max(dp[i - 1][1], -prices[i]);}//毋庸置疑,最后肯定是手里没持有股票利润才会最大,也就是卖出去了return dp[length - 1][0];
}
}
4.最大子序和

看到这道题后,感觉没有什么思路,后来去问了一下ai,感觉茅塞顿开,基本思路是定义一个dp数组,这个dp数组所记录的就是以当前索引为右边界时,这时候的最大子数组,那么递推公式就是dp[i] = nums[i] + Math.max(dp[i-1],0),为什么要有这个代码呢Math.max(dp[i-1],0),这段代码是比较dp[i-1]是否大于0,如果小于零,那么就不能再加了,因为会越加越小,此时从当前索引重新开始记录,为什么会越加越小呢,我当时的疑问是,如果当前索引是一个正数,那不仍然会变大吗,怎么会是越加越小呢,我思索了一会,想明白了,以当前索引的数据来看,如果加上一个负数,那就会变小,不如直接舍弃,重新开始记录,至于当前索引是正数还是负数,这个不用考虑,因为无论是正数还是负数,加上一个负数都会变小。max = Math.max(dp[i],max);,这里则是记录最大值,每次循环都更新max的值,最后返回max。
class Solution {public int maxSubArray(int[] nums) {int length = nums.length;int [] dp = new int [length];dp[0] = nums[0];int max = dp[0];for(int i = 1;i<length;i++){dp[i] = nums[i] + Math.max(dp[i-1],0);max = Math.max(dp[i],max);}return max;}
}
5.打家劫舍

这道题也比较简单,好理解,定义一个dp数组,如果不抢这一家,那能获取的利润有两种情况,一种是抢了前一家,另一种是没抢前一家,比较这两种的最大值,如果抢了这一家,那就只有一种情况,没抢前一家的最大利润。
class Solution {public int rob(int[] nums) {int length = nums.length;if(length == 1){return nums[0];}//定义dp数组int[][] dp = new int [length][2];//不抢第一家的利润dp[0][0] = 0;//抢了第一家的利润dp[0][1] = nums[0];int max = 0;int mid = 0;for(int i = 1;i<length;i++){dp[i][0] = Math.max(dp[i-1][1],dp[i-1][0]);dp[i][1] = dp[i-1][0]+nums[i];//mid用于比较抢和不抢那种利润最大mid = Math.max(dp[i][0],dp[i][1]);max = Math.max(max,mid);}return max;}
}
6.蜗牛

这是一道去年蓝桥杯省赛B组的真题,那么解题思路如下
首先,还是定义dp数组,那状态如何确立,确立状态就是看有几种选择,那么由题可知,蜗牛移动有两种方式,一种是直接爬过去,一种是通过传送门传送,那么可以定义dp[i][0]表示到达第i个结点需要的最短时间,dp[i][1]表示到达第i个传送门的最短时间。
然后就定义初始值,最后写出转移方程就行了
public class Main {public static void main(String[] args) {Scanner scan = new Scanner(System.in);// 在此输入您的代码...int n = scan.nextInt();//定义存储竹竿x轴坐标的数组int [] x = new int[n+1];//定义记录每个竹竿传送门的纵坐标的数组int [] a = new int[n+1];//定义记录被传送到下一个竹竿的纵坐标的数组int [] b = new int[n+1];//输入竹竿纵坐标for (int i = 1; i <= n; i++) {x[i] = scan.nextInt();}//输入传送门的位置和被传送到的位置for (int i = 1; i < n; i++){a[i] = scan.nextInt();b[i+1] = scan.nextInt();}double [][] dp = new double[n+1][2];//dp[i][0]表示到达竹竿底部的最短时间//dp[i][1]表示到达竹竿传送门的最短时间dp[1][0] = x[1];dp[1][1] = x[1]+a[1]/0.7;for (int i = 2; i <= n; i++) {dp[i][0] = Math.min(dp[i-1][0]+x[i]-x[i-1],dp[i-1][1]+b[i]/1.3);if(a[i]>b[i]) {dp[i][1] = Math.min(dp[i - 1][0] + a[i] / 0.7+x[i]-x[i-1], dp[i - 1][1]+(a[i]-b[i])/0.7);}else{dp[i][1] = Math.min(dp[i - 1][0] + a[i] / 0.7+x[i]-x[i-1], dp[i - 1][1]+(b[i]-a[i])/1.3);}}System.out.printf("%.2f",dp[n][0]);}
}
后记
这几天动态规划的题做的比较多,其中有一些也涉及到贪心算法,也了解了一下,下一步我觉得应该就开始学背包问题了,动态规划涉及到了0-1背包问题,感觉是个很经典的问题,背包问题又有很多分支,0-1背包问题只是其中一个小问题,还有很多问题等着我去学习,看了一下去年蓝桥杯的题目,感觉自己还差的有些远,算法掌握的还不够多,接下来就要更加努力去学习了,这一个月就专心准备算法,其他的事情都先放放,等到蓝桥杯结束再说。
相关文章:

Java算法之动态规划
Java算法之动态规划 前言 最近这一段时间一直在刷算法题,基本上一有时间就会做一两道,这两天做了几道动态规划的问题,动态规划之前一直是我比较头疼的一个问题,感觉好复杂,一遇到这样的问题就想跳过,昨…...
)
C++从零开始的打怪升级之路(day47)
这是关于一个普通双非本科大一学生的C的学习记录贴 在此前,我学了一点点C语言还有简单的数据结构,如果有小伙伴想和我一起学习的,可以私信我交流分享学习资料 那么开启正题 今天分享的是关于set和map的知识点 1.关联式容器 在前面&#…...

香橙派AIpro开发板开箱测评
2023年12月,香橙派联合华为发布了基于昇腾的Orange Pi AIpro开发板,提供8/20TOPS澎湃算力,能覆盖生态开发板者的主流应用场景,让用户实践各种创新场景,并为其提供配套的软硬件。香橙派AIpro开发板一经发布便吸引了众多…...
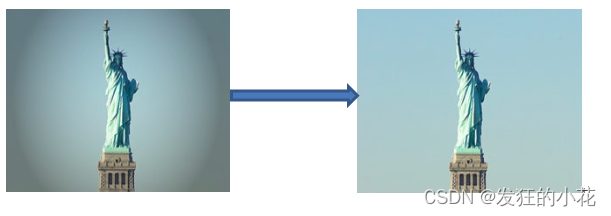
ISP基础概述
原文来自ISP 和摄像头基本知识 本文主要介绍ISP,以供读者能够理解该技术的定义、原理、应用。 🎬个人简介:一个全栈工程师的升级之路! 📋个人专栏:计算机杂记 🎀CSDN主页 发狂的小花 dz…...
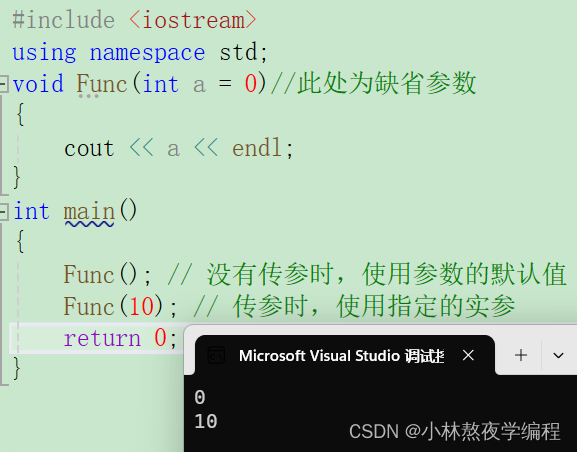
C++第一弹---C++入门(上)
✨个人主页: 熬夜学编程的小林 💗系列专栏: 【C语言详解】 【数据结构详解】 【C详解】 C入门 1、C关键字(C98) 2、命名空间 2.1、命名空间定义 2.2、命名空间使用 3、C输入&输出 4、缺省参数 4.1、缺省参数概念 4.2、缺省参…...

VScode格式化快捷键
vscode格式化代码快捷键 如何使用快捷键格式化代码。使用Java的格式去设置,发现不起作用。 在这里记录一下: 在Windows中,vscode格式化代码快捷键是“ShiftAltF”; 在Mac中,vscode格式化代码快捷键是“ShiftOption…...
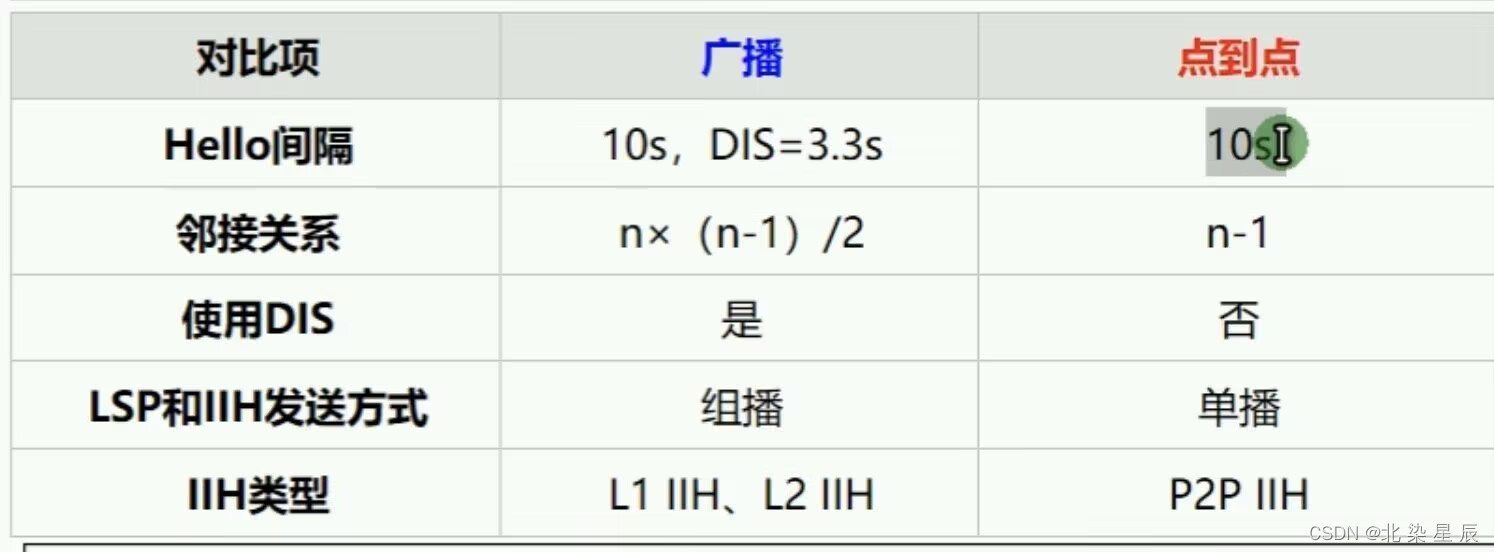
HCIP---IS-IS协议
文章目录 前言一、pandas是什么?二、使用步骤 1.引入库2.读入数据总结 一.IS-IS协议概述 IS-IS是一种基于链路状态的内部网关协议(IGP),它使用最短路径优先算法(SPF或Dijkstra)进行路由计算。这种协议在自治…...
)
突破编程_C++_设计模式(组合模式)
1 组合模式的基本概念 C中的组合模式是一种对象结构型模式,它将多个对象组合成树形结构,以表示具有整体-部分关系的层次结构。在这个模式中,对单个对象(叶子对象)与组合对象(容器对象)的使用具…...
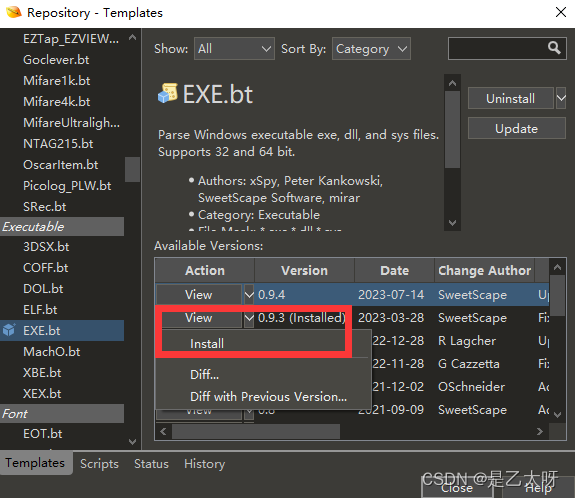
010Editor汉化版+下载+注册码+模板bug
项目场景: 这天我想使用我的不知名的一个破解版本的010Edit来查看一个EXE程序,并想使用模板功能,但是发现没有该模板还无法下载最新模板 问题描述 010Edit联网后需要注册码: 010 Editor 激活码生成器 使用方法 参照教程使用0…...

js【详解】BOM
浏览器对象模型 (Browser obiect Mode 简称 BOM) 浏览器对象即 window,调用window对象的属性和方法时,可以省略window window 常用的属性 Navigator 常用于获取浏览器的信息 navigator.userAgent;火狐浏览器范例: “…...

Leetcode 3077. Maximum Strength of K Disjoint Subarrays
Leetcode 3077. Maximum Strength of K Disjoint Subarrays 1. 解题思路 1. 朴素思路2. 算法优化 2. 代码实现 题目链接:3077. Maximum Strength of K Disjoint Subarrays 1. 解题思路 这道题很惭愧没有搞定,思路上出现了差错,导致一直没能…...

【JetsonNano】onnxruntime-gpu 环境编译和安装,支持 Python 和 C++ 开发
1. 设备 2. 环境 sudo apt-get install protobuf-compiler libprotoc-devexport PATH/usr/local/cuda/bin:${PATH} export CUDA_PATH/usr/local/cuda export cuDNN_PATH/usr/lib/aarch64-linux-gnu export CMAKE_ARGS"-DONNX_CUSTOM_PROTOC_EXECUTABLE/usr/bin/protoc&qu…...

知名比特币质押协议项目Babylon确认参加Hack.Summit()2024区块链开发者大会
Babylon项目已确认将派遣其项目代表出席2024年在香港数码港举办的Hack.Summit()2024区块链开发者大会。作为比特币生态的领军项目,Babylon积极参与全球区块链领域的交流与合作,此次出席大会将为其提供一个展示项目进展、交流技术与创新思路的重要平台。B…...
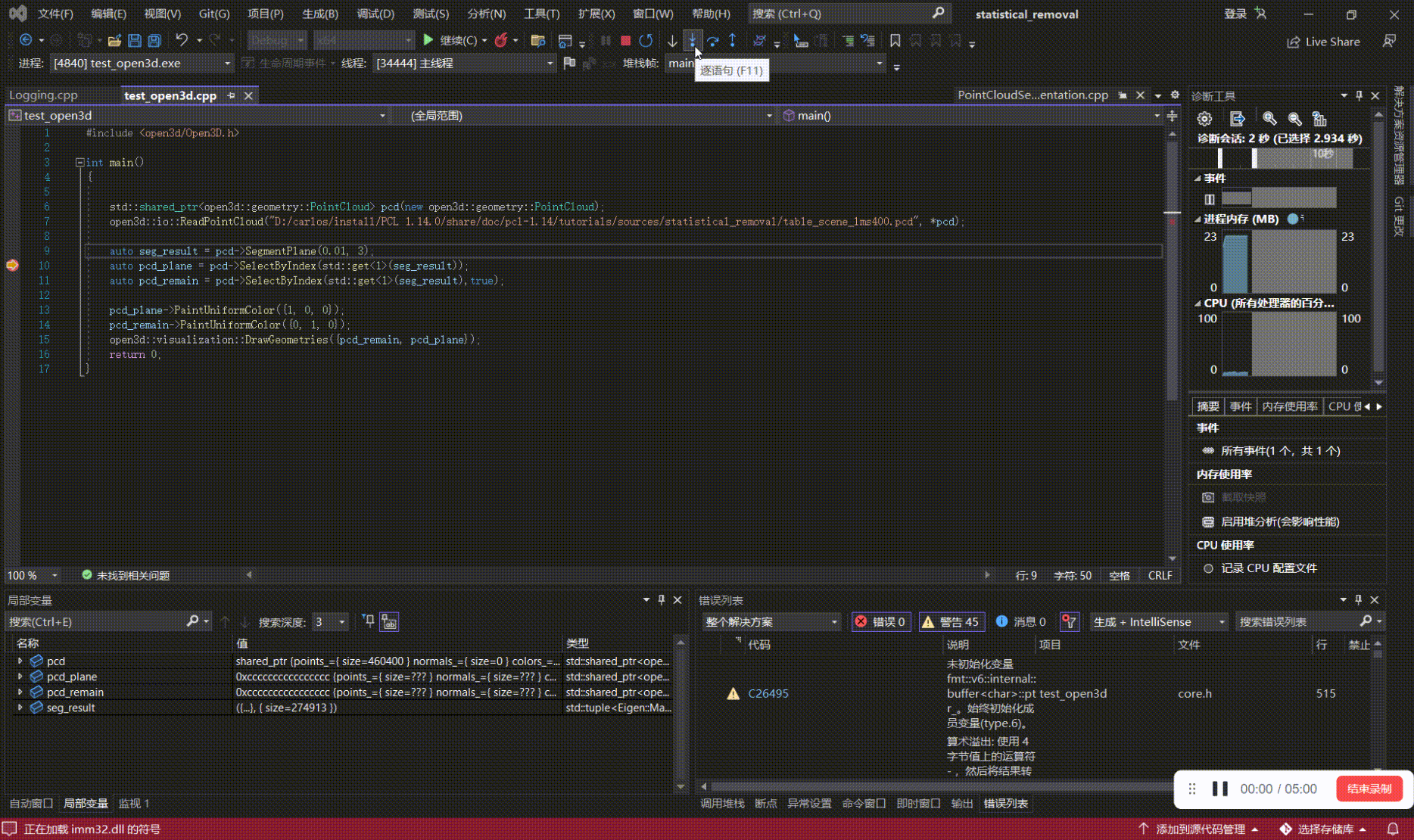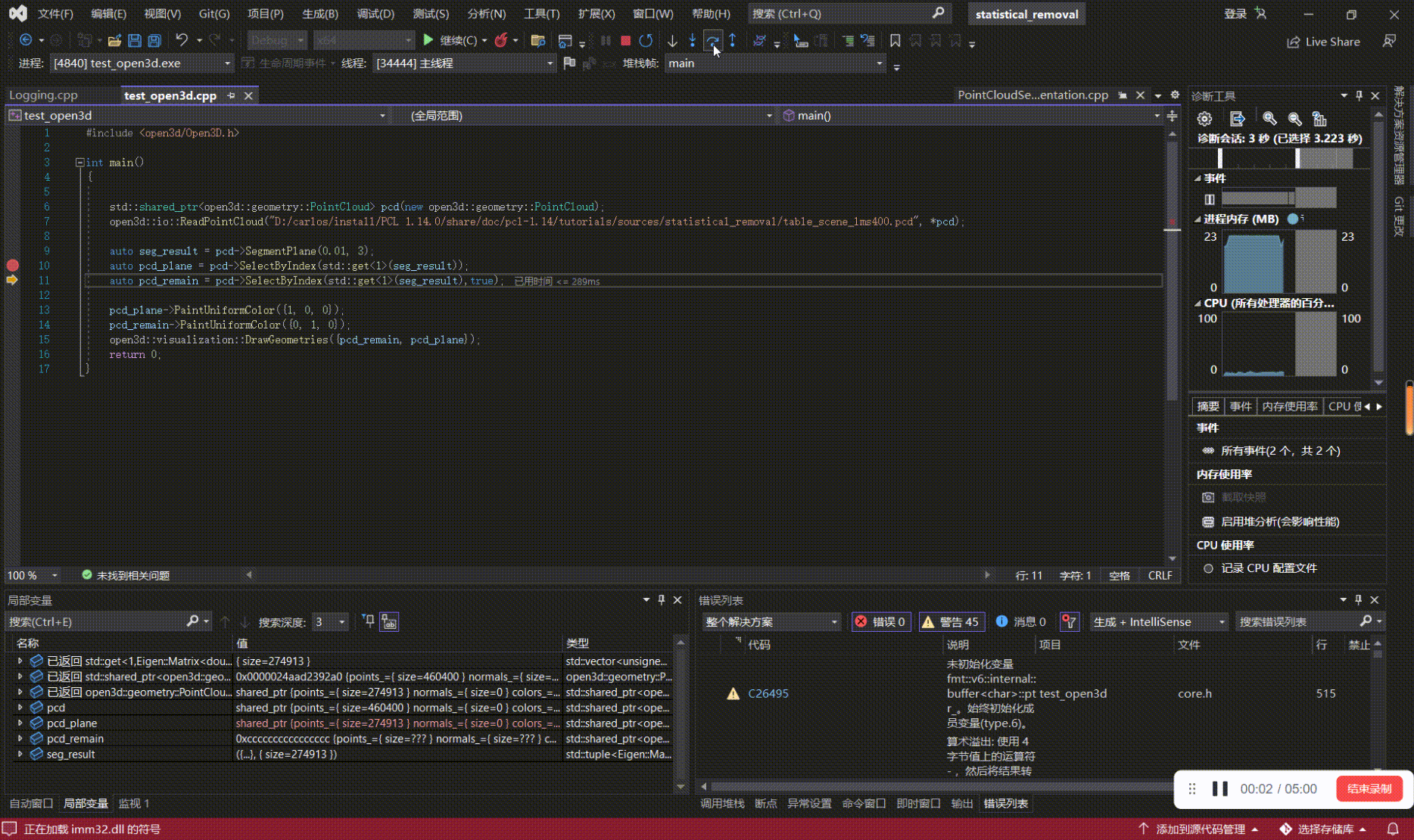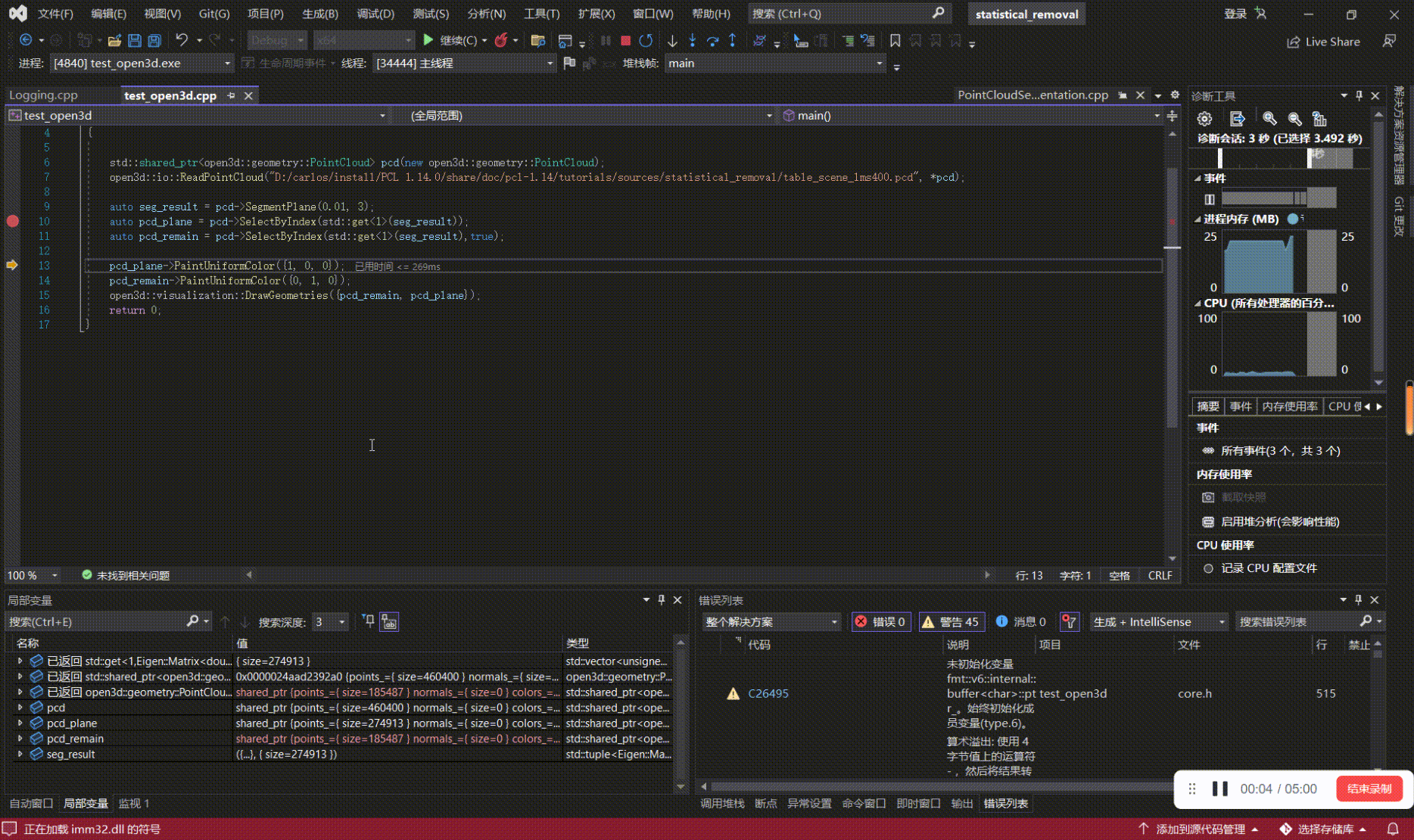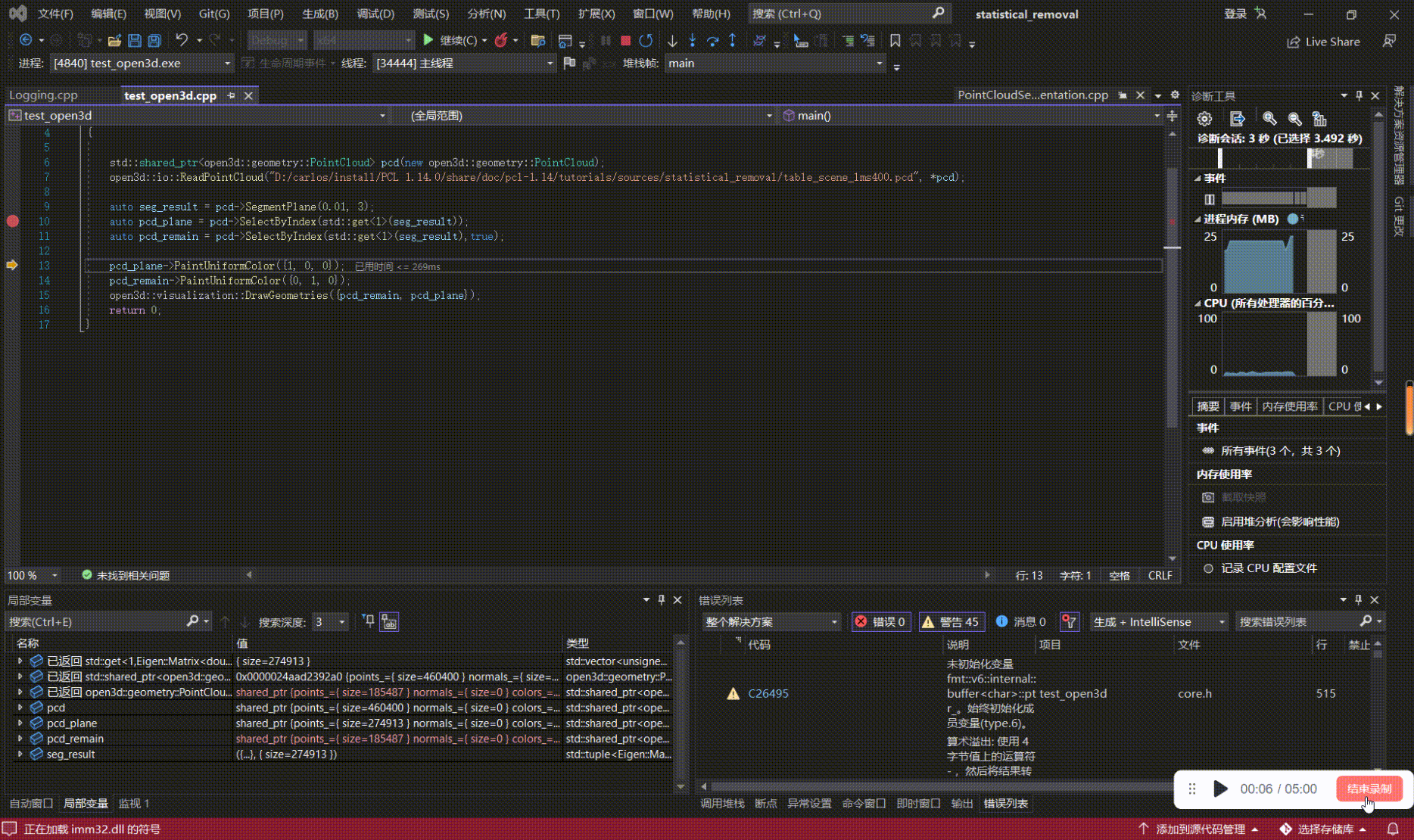
如何学习、上手点云算法(三):用VsCode、Visual Studio来debug基于PCL、Open3D的代码
写在前面 本文内容 以PCL 1.14.0,Open3D0.14.1为例,对基于PCL、Open3D开发的代码进行源码debug; 如何学习、上手点云算法系列: 如何学习、上手点云算法(一):点云基础 如何学习、上手点云算法(二):点云处理相…...

【干货】alzet渗透泵操作说明
alzet渗透泵是一款小型、可植入式的胶囊渗透泵产品,此产品由于其独特的渗透原理,深受广大科研人员的喜爱。该泵可适用于小鼠、大鼠及其他实验动物的研究,并且alzet渗透泵可减轻科研人员夜间及周末给药的困扰。alzet渗透泵无需外部连接或频繁处…...
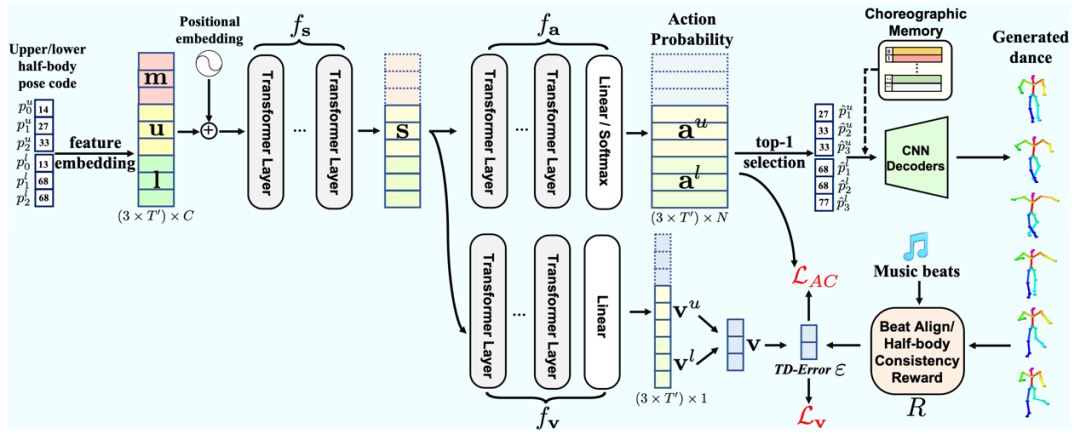
CVPR 2022 Oral | Bailando: 基于编舞记忆和Actor-Critic GPT的3D舞蹈生成
目录 测试结果: 02 提出的方法 测试结果: 预测有3个步骤,速度比较慢 02 提出的方法 1. 针对舞蹈序列的VQ-VAE和编舞记忆 与之前的方法不同,我们不学习从音频特征到 3D 关键点序列的连续域的直接映射。相反,我们先让…...

解读电影级视频生成模型 MovieFactory
Diffusion Models视频生成-博客汇总 前言:MovieFactory是第一个全自动电影生成模型,可以根据用户输入的文本信息自动扩写剧本,并生成电影级视频。其中针对预训练的图像生成模型与视频模型之间的gap提出了微调方法非常值得借鉴。这篇博客详细解读一下这篇论文《MovieFactory:…...
【Python从入门到进阶】50、当当网Scrapy项目实战(三)
接上篇《49、当当网Scrapy项目实战(二)》 上一篇我们讲解了的Spider与item之间的关系,以及如何使用item,以及使用pipelines管道进行数据下载的操作,本篇我们来讲解Scrapy的多页面下载如何实现。 一、多页面下载原理分…...

【调试记录】vscode远程连接问题汇总
1. kex_exchange_identification kex_exchange_identification: read: Connection reset by xxx.xx.xx.x 一直连不上实验室的服务器,用PUTTY和Mobaxterm也不行(报错:Remote side unexpectedly closed network connection)。已知…...

基于springboot的疾病防控综合系统
采用技术 基于springboot的疾病防控综合系统的设计与实现~ 开发语言:Java 数据库:MySQL 技术:SpringBootMyBatis 工具:IDEA/Ecilpse、Navicat、Maven 系统效果展示 用户功能效果 打卡管理 接种记录查看 公告信息查看 社区…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...
